一类树图的第二大特征值

彭海根,吴晓霞,2*

（1.闽南师范大学数学与统计学院,福建漳州363000;2.数据科学与统计重点实验室,福建 漳州363000）

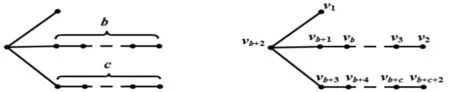
图1 树T(1,b,c)Fig.1 Tree T(1,b,c)

1 预备知识

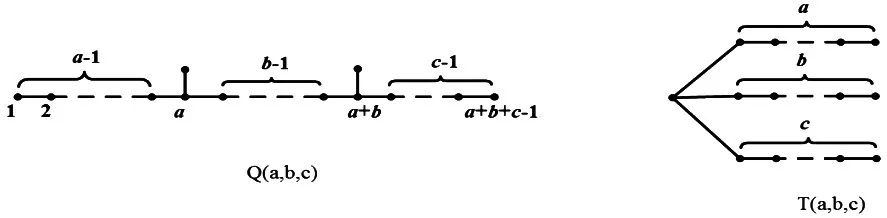
图2 最大特征值属于(2,)的连通图Fig.2 Connected graphs with the largest eigenvalue in(2,)

2 主要结果

下面的讨论主要根据选取树图T(1,b,c)(其中c ≥b ≥5)不同的割点u来得到G -{ }u 不同的子图序列，借助引理5，给出其第二大特征值不同的界，从而得到更好的界.这个界只与其子图Pc,Pc-1,Pc-2,Pc-3有关.根据确定的界可以给出T(1,b,c)依第二大特征值的排序.为了简便后面的证明，我们先计算一些简单结果:

1) 只有一个顶点的图G，有λ1(G)= 0. 事实上，因为只有一个顶点的图G 的特征多项式为χ(G,λ)= λ，所以λ1(G)= 0.

根据图类T(1,b,c)的结构，下面只需讨论图类T(1,b,c)在c ≥b的情形.下面定理2证明中对图G割点u 的选取有两种情形，一种是使图G -{u } 的分支H1和H2结构相同顶点数尽可能相等，以此得到更好的界，另一种是先选一个使λ1(H1)尽可能小的割点，得到λ2(T(1,b,c))的上界，再选一个使λ1(H2)尽可能大的割点，得到λ2(T(1,b,c))的下界.

定理2 设树图G = T(1,b,c)，若c ≥b ≥5，则

定理3 设树图T(1,b,c)，其中c ≥b ≥7，则有λ2(T(1,b - 2,c + 2))＞λ2(T(1,b,c)).

证明 当b + 2 ≥c ≥b 时，由定理2 中1)的证明知λ1(Pc)≥λ2(T(1,b,c)). 因为b ≥7，所以b - 2 ≥5，又因 为6 ≥c + 2 -(b - 2)≥4，所 以 由 定 理2 中2)的 证 明 可 知λ2(T(1,b - 2,c + 2))＞λ1(Pc). 因 此λ2(T(1,b - 2,c + 2))＞λ2(T(1,b,c)).根据定理2中1)的证明知，当c = b + 3时，λ2(T(1,b,c))= λ1(Pc-1)，又因为当c ＞b + 3 时，由定理2 中2)和3)的证明知，λ1(Pc-1)＞λ2(T(1,b,c))，所以当c ≥b + 3 时，λ1(Pc-1)≥λ2(T(1,b,c)). 当c ≥b + 3 时，c + 2 -(b - 2)≥7，由定理2 中3)的证明知λ2(T(1,b - 2,c +2))＞λ1(Pc-1)，所以λ2(T(1,b - 2,c + 2))＞λ2(T(1,b,c))，证毕.

3 总结

根据引理5中结果,对树图T(1,b,c)割点进行选取得到其第二大特征值的界，为了确定第二大特征值的分布,采用两种方式选取树图T(1,b,c)的割点,一种是选取使H1和H2结构相同顶点数尽可能相等的割点，另一种是先选一个使λ1(H1)尽可能小的割点得到T(1,b,c)第二大特征值的上界,再选一个使λ1(H2)尽可能大的割点,得到T(1,b,c)第二大特征值下界.所用的方法可以用来考虑结构相对对称的图的第二大特征值如Q(a,b,c),或用来比较结构相似的图的第二大特征值的大小.另外，对于没有割点的连通图G，可以考虑图G - U各个分支的最大特征值与图G的第二大特征值的关系，其中U为割集且 ||U ≥2.