基于迁移学习的多任务分配算法

王梦娇，尹 翔，黄宁馨

扬州大学 信息工程学院，江苏 扬州 225009

1 引言

随着现代社会与科学技术的飞速发展，人们面临的问题变得日趋复杂。分布式系统成为解决复杂问题的有效手段和方法。通过将复杂任务分解为相对简单的子任务，再将子任务分配给各智能体（agent），可以有效提高任务求解效率[1-2]。因此，任务分配问题已经引起了学术界和工业界的广泛关注。

任务分配的目的是找到一种合理的子任务分配方式，使得子任务能够被高效、合理地分配给各智能体。已有众多学者对该问题展开深入研究。Smith 等人[3]提出了合同网协议，通过在多个智能体间订立合同，以协商的方式实现任务的分配。以合同网协议为基础，刘海龙等人[4]基于集合覆盖理论提出了一种在合同网框架下解决子任务分配的严格启发式搜索算法，并分析了算法的收敛性及时间复杂度。Cano 等人[5]研究了如何将软件分配给硬件处理器的问题，将该问题建模为一个多目标优化问题，并给出了一个基于约束优化的算法。

近年来，随着人工智能技术的飞速发展，已有学者将强化学习的相关理论和方法用于求解任务分配问题。Liu 等人[6]给出了一种基于强化学习的云资源分配机制，该策略通过在线学习实现了云资源的自动管理和分配，提高了系统效益。廖晓闽等人[7]针对移动通信中的蜂窝网资源分配多目标优化问题，提出了一种基于深度强化学习的网络资源分配算法。这类方法将任务分配问题建模为一个马尔科夫决策过程，通过最大化回报函数来获得最优策略。

现有的大部分研究都是将任务分配问题建模为多目标优化问题，通过求解最优解来获得最优分配策略。然而，作为一类NP-complete问题，计算最优解将耗费大量资源，在问题规模较大时，甚至是不可能的。另一方面，对一个系统而言，其所面对的任务通常具有一定的相似性，如果能够利用这种相似性来指导任务的分配，可以提高新任务分配的效率，获得更多收益。

迁移学习作为机器学习的一个重要分支，已在任务规划[8-9]、图像处理[10-11]以及众包[12-13]等领域有广泛应用。迁移学习的核心思想是找到源任务与目标任务之间的相似度，从而将一个或多个与目标任务相似的源任务的知识或策略进行迁移[14-15]。可见，通过迁移学习，可以使agent 在面对新任务时充分利用已有的经验和知识，在一个较高的起点上对问题进行求解，提高任务求解的效率。

基于此，本文讨论了多智能体环境下的任务分配问题。所提出的算法利用迁移学习找到与目标任务最匹配的源任务，将其任务分配方案迁移到目标任务中，加速任务的分配。同时，在智能体寻找最优路径的过程中利用迁移学习，通过历史经验加速学习过程。实验表明，相比于传统的强化学习方法，本文算法运行时间大幅度降低且性能明显提升。

2 问题描述

本文算法解决的是在一个目标任务中，有多个子任务需要由多个智能体来完成的问题。本文算法将迁移学习的思想引入多任务分配的问题中，目的是为了在保证任务分配质量的情况下，提高任务分配的效率。如图1所示，在本文的模型中，有多个智能体（数字表示）和多个子任务（Δ 表示），中央控制器将子任务分配给智能体，智能体需要找到一条到子任务位置的最优路径。智能体的状态集合用S表示，包含智能体能到达的任意位置。智能体的动作集合用A表示，包含上、下、左、右四个动作。每次智能体只能移动一步。在这里，子任务的坐标或智能体的状态由离散坐标表示，黑色实心部分表示障碍，智能体无法到达或穿过。

图1 多智能体完成多子任务

下面是对本文所解决的问题的形式化描述：假设系统中有一定数量的智能体，其集合记为Agent，即Agent=，其中，n表示智能体的数量，源任务的子任务集合为SourceTask，即有其中，m表示源任务中子任务的数量，目标任务的子任务集合为TargetTask，即有其中，g表示目标任务子任务的数量。智能体数量与子任务数量的关系是n≥m，且一个智能体最多只能完成一项子任务。算法的目标是最大化平均带折扣回报，即，其中，k表示片段数，H表示一个片段结束所用的步数或所允许的最大步数，γ表示折扣因子，ri,h表示第i个片段的第h步得到的立即回报。

3 算法设计

本章阐述本文提出算法的基本思想，算法中迁移的知识是策略。首先，将一定数量的源任务对应的策略构成一个策略库表示策略库中策略的数量，即源任务的数量；接着，在解决目标任务时，中央控制器要根据相似性度量找到与目标任务相似程度最高的源任务，将该源任务的智能体分配策略迁移到目标任务中；得到目标任务分配策略之后智能体将该源子任务的知识进行迁移来学习一条到达目标子任务状态的最优路径，提高了学习效率并减少损耗。

3.1 算法介绍

本文算法分为两步：首先找到与目标任务最相近的源任务，将源任务的任务分配方式迁移到目标任务中，再使用迁移学习来学习并获得各智能体到其对应的目标状态的最优策略。具体算法如下：

首先，让智能体学习一组具有代表性的、可以充分表示各种类型任务的源任务。源任务的作用是与目标任务相匹配，进行子任务分配策略的迁移。源任务库的构造方法：计算当前源任务与源任务库中已有的任务的相似性，若相似性较差，将当前源任务加入源任务库中，并将已学习的策略存入策略库StrategyLibrary中。当目标任务到来时，中央控制器要分别计算目标任务中各个子任务与源任务中的子任务的考虑障碍的最小哈夫曼距离和，距离和最小的源任务判定为与目标任务最相似的源任务，记为most_matched。将策略库中该源任务的策略πmost_matched（即子任务的分配策略）迁移到目标任务中，其中，距离和的计算还考虑到了目标子任务与源子任务和障碍的相对位置。最后，中央控制器根据目标任务中子任务的坐标和对应智能体之前处理过的子任务的坐标之间的哈夫曼距离判定源子任务与目标子任务之间的相似度，将相似度最高的源子任务的策略迁移到目标子任务中。算法的整体思路如算法1所示。

算法1 带迁移的多智能体多任务分配算法

输入：

1.源任务库对应的策略库StrategyLibrary

2.一组目标任务的集合Ω

初始化：

forj=1 togdo

1.分别计算目标任务中的子任务与各源任务的子任务的（考虑障碍的）距离，再求和得到distance

2.most_matched=arg minsource_taskdistance即选取距离和最短的源任务作为被迁移的任务

3.πtarget←πmost_matched将选定的源任务对应的策略迁移给目标任务的智能体

4.利用迁移学习算法找到智能体到其对应子任务的目标位置的最优路径

end for

算法2的重点是如何比较任务之间的相似度，通过子任务之间的相似性度量找到与目标任务最相似的源任务。若将与目标任务相似度不高的源任务的策略进行迁移，则很有可能会产生负迁移，即进行迁移之后的策略反而比从头学习策略效果更差。为了减少负迁移的产生，计算距离的公式如（1）所示，其中，distanceij表示目标任务中第j个子任务与源任务中第i个子任务之间的距离。

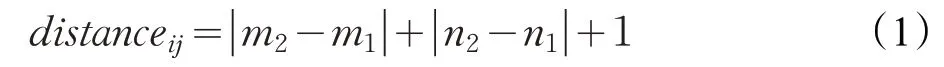
如图2所示，当两个子任务之间存在障碍，则distanceij会被赋予很大的值，表示源任务中的子任务i与目标任务中的子任务j相似度不高。若只考虑哈夫曼距离，那么这两个子任务的哈夫曼距离是比较小的，但实际上因为智能体不能穿过障碍，故要绕开障碍，说明这两个任务的相似度不高。比较源任务与目标任务的相似度的伪代码见算法2。

图2 任务相似性度量

算法2 计算源任务与目标任务的相似度

找到包含所有best_agent的源任务

目标任务中的各个子任务分配好之后，进入算法的第二阶段，即利用迁移学习计算各智能体到目标子任务的最优路径。这里，各智能体之前处理过的源子任务与其对应的目标子任务的相似度的计算方法与算法2 类似，不做赘述。算法3表示的是利用迁移学习找到一条从智能体到目标子任务的最优路径的伪代码。其中，Episodes表示寻找最优路径的最大片段数。

在算法3 中，源任务的子任务的策略被保存在pai中。为了平衡“利用”和“探索”，使用了pt和p_t两个变量进行控制。pt表示片段的第一步“利用”历史经验的概率，其随片段数的增加不断减小，即随着片段数的增加，智能体越少地“利用”历史经验，也就是智能体更多地“利用”自身学习的知识。原因在于使用迁移学习的目的是在前期给智能体一个较好的指导，但由于源任务和目标任务是不完全相同的，故不能一直“利用”源任务中的策略。pt的更新公式如式（2），分母中的参数500是针对本实验尝试不同参数值之后效果最好的参数值。不同参数值的性能比较见实验部分。

算法3 学习智能体到目标子任务的最优路径

输入：

与目标子任务最相似的源子任务most_match_source

初始化：

1.每个片段的第一步利用历史经验的概率p_t=1

2.带折扣的奖励之和sum_rewards_transfer=0

在一个片段中，“利用”历史经验的概率p_t也是随步数的增长下降的。该变量的意义在于在一个片段中“利用”历史经验的频率逐渐降低。两个变量共同作用下，使得智能体随着片段数、步数的逐渐增加，“利用”历史经验的频率逐渐下降。

3.2 算法分析

本节对本文提出的算法与基于Q 学习的基本搜索算法从时间复杂度方面进行比较和分析。

假设源任务有m个，每个源任务中平均有s个子任务，目标任务中有g个子任务，系统中有n个智能体，k表示学习最优路径过程中的迭代次数。那么在带迁移学习的情况下，第一步将子任务分配给合适的智能体所需要的时间复杂度为，第二步学习智能体到对应子任务位置的最优路径所需要的时间复杂度为，故总的时间复杂度为。而用基于Q学习的基本搜索算法进行迭代求解，那么时间复杂度为，这里有m≪k，故相比较而言，本文提出的算法的时间复杂度要远低于基于Q 学习的基本搜索算法。

4 实验与结果

为了验证算法的性能，本文实验的环境建立在“格子世界”模型之上。从算法运行时间、平均带折扣回报等方面将文中的算法与基于Q 学习的基本搜索算法进行对比。本章首先介绍了实验模型，接着展示了两种算法的性能并进行分析。

4.1 实验模型及参数设置

实验模型如图1所示，环境被分为18×27个小格，黑色部分表示障碍，若智能体执行某动作之后遇到障碍则停在原地。智能体每走一步只要不到达终点所获得的立即回报为−1，智能体碰到障碍得到−10 的惩罚，到达终点得到+10 的立即回报。图中数字部分表示智能体的位置，本实验中一共有14 个智能体且智能体的位置固定，图中Δ 表示子任务的位置，子任务的位置是不断变动的，每个任务中子任务的位置不同，且子任务的数量也不一定相同。此处假设智能体最多只能完成一个子任务，故子任务总数小于智能体总数，并且本实验考虑子任务数较多的情况，因为子任务少的情况下，可选择的智能体较多，不科学的选择对结果的影响较小，故子任务数最小为10，若表示子任务的数量，设。为了表示实验的一般性，目标任务的子任务位置是随机产生的。在实验中，源任务中各子任务位置是随机生成的，均匀分布在图1 所示的各子区域中。

传统Q学习算法中使用的是ε-greedy策略，参数的设置考虑到实际情况和Fernando[16]文中的参数，具体如下：ε=0.01 表示Q 学习算法有1%的概率进行“探索”，99%的概率进行“利用”；γ=0.9 表示折扣因子为0.9；α=0.05 表示学习速率为0.05，Episodes=2 000 表示智能体最多迭代2 000 次学习最优路径，该迭代次数可以保证算法收敛到最优路径。在实验中，由于本文提出的算法解决的是多智能体环境下的多任务分配问题，其本质是一个序列决策问题，而Q学习是解决这类问题的经典算法，故此处与基于传统Q 学习的任务分配方法进行比较，以验证本文算法的性能。相较于其他路径规划算法，如A*算法，基于迁移学习的算法的优势在于其不需要知道环境的准确模型，而通过不断试错得到最优路径。实验环境：Intel i5 CPU，4 GB RAM 以及Python 3.5。

4.2 实验结果与分析

第一组实验的目的是比较基于Q 学习的基本搜索算法与本文提出的算法之间的算法运行时间和准确度。本组实验共有21 个目标任务，每个目标任务中的子任务个数是随机的，表1展示了21组目标任务找到对应的智能体所需要的平均时间。

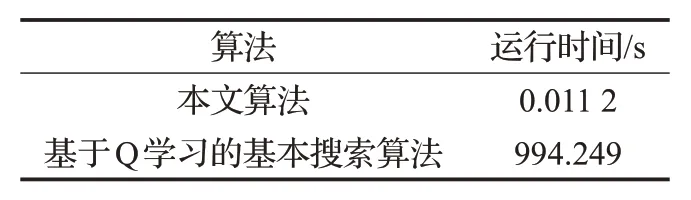
表1 算法运行时间比较

从该组实验可以得出，利用基于Q学习的基本搜索算法所消耗的时间远高于本文提出的算法，其原因在于利用历史经验，目标任务的解决无需穷举每种情况，而基于Q 学习的基本搜索算法由于每次获得最优路径的消耗时间较多，再加上该过程要迭代多次，故时间较长。本文提出算法的最大优势是大大降低了算法的运行时间，对于实时性要求较高的任务，其性能比基于Q学习的基本搜索算法好。

第二组实验分析了不同子任务数对任务分配算法的运行时间的影响。图3 展示了两种算法的运行时间的对比。从图中可以看出，当目标任务的子任务数为10时，基于Q 学习的基本搜索算法的运行时间为800 s 左右，子任务数为11 时，运行时间波动不是很大，子任务数为12时，运行时间接近950 s，当任务数为13时，运行时间接近1 200 s，而本文提出的算法在运行时间上花费较少且波动不大。原因在于基于Q 学习的基本搜索算法在计算每个智能体到目标任务的最短路径之后再选出可以到子目标任务最快的智能体，从而找到能解决目标任务最优的智能体集合，故受子任务数的影响较大。而本文提出的算法利用了历史经验进行任务分配，仅通过比对任务之间的相似度，将最相似的源任务的分配方案迁移到目标任务中，故任务分配的耗时较少且几乎不受子任务数的影响。

图3 不同任务数的运行时间

第三组实验显示了pt更新公式中不同参数值的性能比较，结果如图4 所示。其中，参数的范围值为50 至1 000。

图4 不同参数值的性能比较

第四组实验显示了在学习最优路径中，使用迁移学习和不使用迁移学习的对比，从第一个片段和最后一个片段的平均带折扣回报方面进行对比与分析。图5 显示了某个随机产生的目标子任务的最优路径学习过程中，使用不带迁移学习和带迁移学习的平均带折扣回报的对比。从图中可以看出，带迁移学习的算法在初始时就有比较好的平均带折扣回报，且在执行过程中，该值都比不使用迁移学习要高，这表明本文提出的算法缩短了智能体找到最优路径所需的时间。

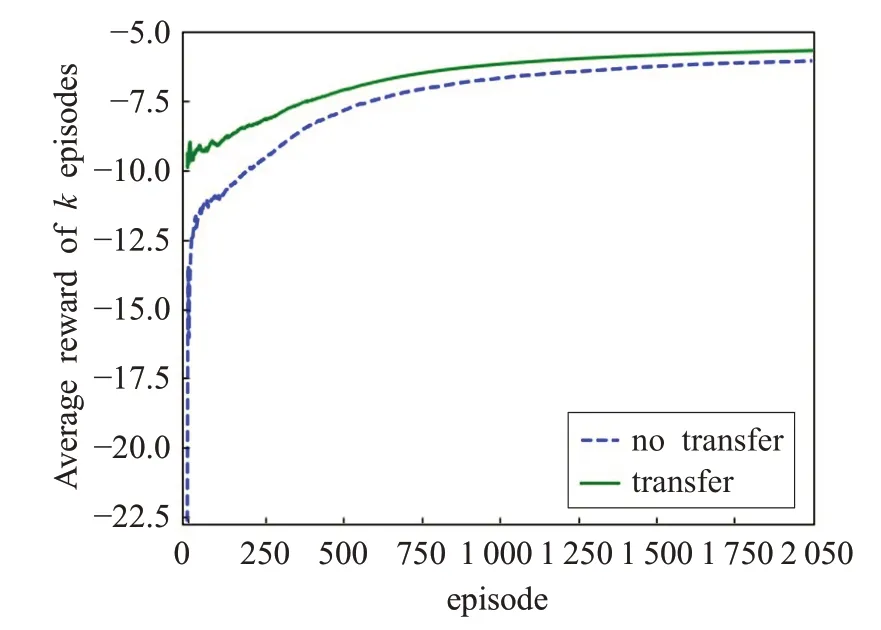
图5 子任务带迁移与不带迁移的平均带折扣回报

表2 显示了一个目标任务中各子任务在带迁移学习和不带迁移学习上平均带折扣回报的对比。从表中可以看出，使用迁移学习可以在初期给智能体较好的行为指导。其中，[9，6]这个子任务在第2 000个片段的带迁移平均带折扣回报比不带迁移的低，这是由于在分配任务阶段，分配给的智能体不同而导致的。对于任务分配的准确度问题也是以后需要进一步研究、改进之处。

表2 带迁移与不带迁移的平均带折扣回报对比

5 总结与未来工作

本文主要研究了多智能体系统中的多任务分配问题。提出了一种基于迁移学习的任务分配机制。首先将目标任务与源任务库中的任务进行比较，找到与目标任务最相似的源任务，将策略库中对应的智能体的分配方案迁移到目标任务中，给目标任务较好的初始化，加速目标任务的分配。本文还利用迁移学习加快智能体学习最优路径的速度，即将智能体之前处理过的子任务的策略迁移到目标子任务的完成上。通过实验可以看出，本文提出的算法在运行时间和平均带折扣回报上均优于基于Q学习的任务分配算法。

未来的研究方向包括：首先是要解决鲁棒性不够的问题，可从相似度的比较方法方面进行改进；其次，若目标任务的状态空间和行为空间产生变化，要如何将源任务的策略进行迁移，如何防止因状态空间或行为空间的变化而带来的负迁移情况。