基于二元对称多项式的秘密共享方案

禹亮龙，杜伟章

长沙理工大学 计算机与通信工程学院，长沙 410114

1 引言

秘密共享是数据加密中重要技术，也是信息安全中一个重要研究方向，它在密钥管理、数字签名和多方计算等领域起着关键作用。在1979年，由Shamir[1]和Blakely[2]提出两种不同的(t,n)门限秘密共享方案，分别是基于Lagrange 插值法和射影几何理论提出。在(t,n)门限秘密共享中，秘密S将被可信中心（即分发者）D分成n个份额，并且满足以下条件：（1）恢复出秘密S需要任意t位或者t位以上的有效份额；（2）如果有效份额少于t个，则秘密S不能被计算出。

现有的许多的秘密共享基本都要求参与者一直诚实的情况下进行的。但是，在恢复秘密的过程中，不可避免地存在着内部欺骗者或者外部欺骗者，比如存在非法外部参与者加入到秘密恢复中，使得秘密泄露，也有可能存在内部参与者进行欺骗行为，使得只有自己能够计算计算得出秘密，其他参与者得到错误的秘密。一种情况是，当有m(m>t)位合法的参与者加入秘密恢复阶段时，假设参与者交换份额不是同步的，那么就有可能有一个无效份额的持有者参与恢复，通过恢复时的安全信道，至少能够获得t个有效份额，那么外部欺骗者就能够恢复正确的秘密，使得秘密泄露。另一种情况是，拥有有效份额的持有者与其他参与者交换份额时，使用的是错误的份额，但是欺骗者却可以得到有效份额，那么就会造成只有内部欺骗者才有可能计算出正确的秘密。针对上面的情况，要保证方案的公平性，即如何确保：（1）有且仅当参与者提供的份额都为有效时，才可以计算出正确的秘密。（2）当有错误的份额或者份额不全时，正确的秘密就不能被解出。目前，主要研究的方面是方案的公平性以及可验证性。

Chor[3]于1985 年首次提出了可验证秘密共享的概念，通过填加份额验证，来防止欺骗者。近几年来，随着信息安全技术的深入研究，越来越多的秘密共享方案[4-10]也被相继提出。但是在大多数方案中，可信中心为参与者计算并分配秘密份额，并通过信道发送给他们，这会导致分发者持有的信息数大，权利过重等问题，这样也导致分发者需要进行的计算量大并容易遭受攻击。1987年，Feldman[11]提出了一种新的秘密共享方案，在不需要可信中心的第三方参与的情况下，能够抵抗(n-1)/2位内部欺骗者或者外部欺骗者的合作欺骗。1994年，Harn[12]提出了一种不需要可信中心的门限群签名方案。2003 年，王斌和李建华[13]对Harn 的签名方案进行分析，并指出其中的不足，并提出了一种新的无可信中心的门限签名方案。2007年，庞辽军等人[14]提出了一种不需要可信中心来分发份额的秘密共享方案，但还是需要可信中心来选择份额的一些参数和计算一些公开信息。2016年，于佳等人[15]提出了一种可验证的多秘密共享方案，可以同时对多个秘密进行分发。2017年，彭巧[16]的可验证方案；2018 年，张艳硕等人[17]的基于特征值的无可信中心的秘密共享方案研究等。

2 预备知识

2.1 Shamir(t,n)门限秘密共享方案

方案分为份额分发和秘密恢复两个阶段。

份额分发阶段：分发者D随机选择一个t-1 次多项式，秘 密S=a0∈分发者D选择{x1,且xi≠0 为每个份额持有者Ui的身份信息。D为Ui计算份额，并通过安全信道发送给Ui。

2.2 二元对称多项式

在有限域GF(p)上，一个典型的t-1 阶二元多项式为如下形式：

其中p为大素数，其中根据二元多项式的特性，又可以将其分为两大类：二元对称多项式和和二元非对称多项式。假如二元多项式的系数全部满足ai,j=aj,i，则称该二元多项式是对称的；如果不能全部满足，则是非对称的。

其中二元对称多项式有着明显的对称性，假设二元多项式f(x,y) 是二元对称多项式，那么对于有限域GF(p) 中的任意两个整数xi和xj，f(x,y) 一定满足f(xi,xj)=f(xj,xi)。利用二元对称多项式实现秘密共享的方案主要有文献[18-20]等。在上述方案中，都需要一个可靠的分发者来构造多项式和分发份额，使得分发者计算量大，掌握数据过多。

3 方案构成

3.1 初始化阶段

设S是共享秘密，是n位参与者的集合。Pi选择自己的身份标识IDi，并公开；然后构建t次的对称二元多项式：

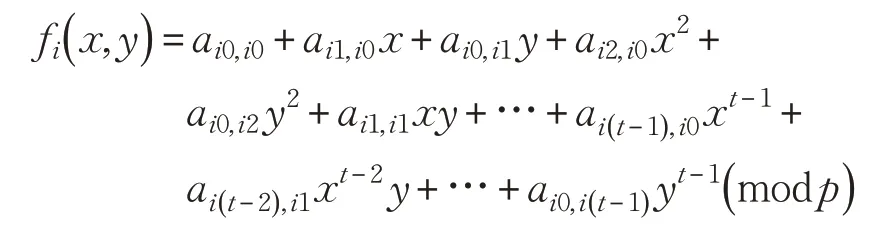
p为大素数，GF(p)为p阶有限域。参与者共同选出随机数Pi计算并公布。

3.2 秘密分发

参与秘密共享的人，共同选出验证参数e1和e2(e1,，Pi计算和，并发送给。

3.3 恢复阶段

参与恢复的m位Pi做如下操作：

Pi接收Pj发送的内容后，计算份额，和：

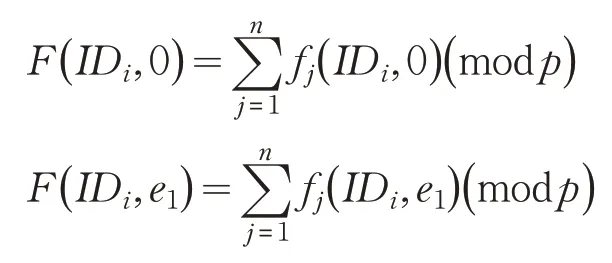
Pi在与参与者交换份额，先进行交换验证，判断Pi发送的是否等于Pl发送的，如果不相等，则Pl为欺骗者，通过广播公布欺骗者并停止发送份额。如果相等，则发送份额和：

Pi在接受Pj传递的和后，通过Lagrange 插值公式计算出和：

并将e1,e2,0 代入比较，如果，和都同时成立，则计算S'=F0( 0)=，检验结果的正确性，参与者Pi计算和，并比较是否相等：

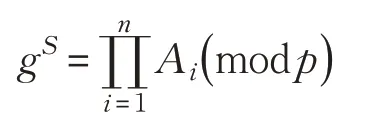
4 分析与比较

4.1 正确性分析

在本文方案中，当m(t≤m≤n)位合法且诚实的份额持有者能够恢复出真实秘密S。

证明首先m位参与者在分发阶段结束后，Pi可计算得出各自份额，以及和：

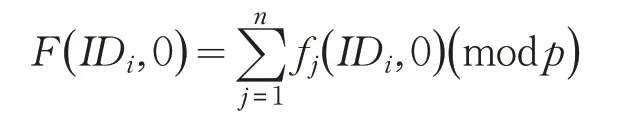
在份额交换前的验证，能尽可能的保证Pi获得的份额是正确的，根据Lagrange 插值公式公式可知，至少需要t个因子可恢复t-1 阶多项式，才能解出S。保证了有效的参与者能够恢复出秘密S：

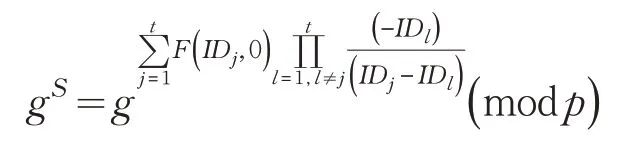
4.2 安全性分析

当参与恢复的人中存在内部欺骗者时：

假设内部欺骗者Pi提供了不真实的份额F'( )IDi,0 ，在计算出S'后的检验结果正确性时，会被检测检测会出，而在Pi提供的a'i0,i0阶段，如果提供真实的ai0,i0，通过检测后，其他参与者可以计算出很正确的S，即

如果Pi提供不真实的a'i0,i0，则其他参与者可以计算，并与Pi初始化阶段公布的Ai比较来判断正确性。

当有外部欺骗者Di存在时：

首先如果Di是在秘密恢复恢复阶段才参与的，那么他是没有其他份额持有者发送的，和，在交换验证阶段只有的概率能全部通过；假设Di通过了交换验证，并获得了初始阶段分发的和，没有正确的，计算出。

4.3 方案分析比较

近几年基于二元多项式的秘密共享方案，大多是要求有一个安全的可信中心来构造多项式和分发份额的，而本文方案是一个无可信中心的秘密共享方案，即消除了可信中心可能带来的风险，增加了方案的安全性。

高效性：与张艳硕的方案相比，本文在初始化和恢复阶段的效率高很多，张艳硕的方案在初始化阶段，分发者需要计算k对序列，并找出一个最小值。恢复阶段，参与者需要从第一队序列开始查找，每次查找都需要计算新的份额，并进行验证，直到找出转折点，即秘密S才结束，最坏的情况是需要重复恢复k-1 次；而本文方案，分发结束后，参与者就可以计算出唯一的份额，如果份额正确，技能得出正确的秘密S。

异步性：与Liu 的方案相比[20]，本文方案中，任意两名参与者拥有私有的通话密钥，防止外部欺骗者获得有效份额，并不需要所有参与者同时交换信息和验证；而Liu的方案，由于份额是在恢复前，参与者会广播一些份额信息，如果人在人数超过门限值时，有外部欺骗者进入，并获得了其他t个份额，则有可能得出秘密。

5 结束语