局部迭代的快速K-means聚类算法
2020-07-06李明祥张宇敬
李 峰,李明祥 ,张宇敬
1.河北金融学院 信息管理与工程系,河北 保定 071051
2.河北省高校智慧金融应用技术研发中心,河北 保定 071051
1 引言
近些年,非监督学习情况下的数据聚类分析研究不仅在理论上取得了长足的发展,如文献中提到的ET-SSE[1]、OLDStream[2]、k-MS[3]、SDPC[4]及最小误差平方和K-means初始聚类中心优化[5]等算法,并且还广泛应用于图形图像处理[6]、文本分析[7]、视频处理[8]、网络舆情分析[9]、交通导航和各类推荐系统等各个领域。K-means 模型是最基本和最重要的聚类算法之一。该模型在欧几里得空间定义了包含n个向量元素的数据集D={d1,d2,…,dn},目的是把n个向量元素分配到k组不同的聚类簇中S={S1,S2,…,Sk},其目标函数是:

其中S代表聚类结果,Cost(Si)表示聚类簇Si中所有数据点到聚类中心的距离平方之和,表示为:
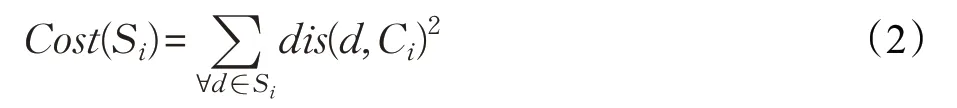
其中dis(d,Ci)表示数据点d与Ci的距离,Ci表示聚类簇Si的中心。为了使目标函数Cost(S)的取值最小,K-means算法的基本执行过程为:第一步,随机选取k个点作为聚类中心的初值;第二步,把数据集中的n个数据分配到最近的聚类中;第三步,更新每个聚类的中心;第四步,重复执行第二步和第三步直到目标函数趋于收敛为止。虽然K-means算法是一个高效的算法,但是它依赖初始化中心的选择,好的聚类中心初值能够提高聚类的速度和聚类的效果。因此,很多关于聚类中心初始化的算法就被提了出来。
Arthur等人[10]提出的K-means++算法是从数据集中随机选取一个数据作为第一个聚类的中心,之后第i个聚类中心的选取,满足下列概率条件:
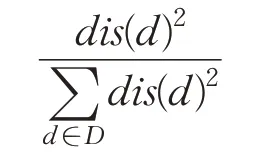
其中,dis(d)表示数据点到最近中心的距离。该方法认为初始聚类中心应该离的越远越好,这样就可能会把相邻的多个小聚类当成一个庞大的聚类进行处理,影响聚类的精确度。
Chowdhury等人[11]提出的Seed Point Selection algorithm算法,通过使用具有距离约束条件的像素强度的联合概率最大化概念来选择种子点。此方法虽然优化了聚类中心的选择,但由于最优聚类数是基于7个不同的聚类有效性指数的组合来确定的,所以该算法的计算过程相对比较复杂,在最终的聚类效率上会有一定的损失。
Tzortzis 等人[12]提出的 MinMax 版本的K-means模型改变了目标函数,利用最大的簇内方差εmax代替Cost(S)作为潜在的目标函数。该方法会根据他们的方差为聚类分配权重,通过迭代过程不断更新权重和聚类中心,避免了大方差聚类的出现。如果绝对的限制大方差聚类的出现,在一些实际应用中可能会造成聚类效果的误差,从而引起数据分析的结果不够准确。
此外,除了以上关于选择聚类中心初值的算法,还有关于提高K-means 聚类速度的算法也被提了出来。通过特征选择或特征提取能够降低数据集的维度从而提高K-means聚类的速度。特征选择不同于特征提取,特征选择是选择一个小的输入特征子集;而对于特征提取,则是基于输入数据集重新构建新的人工特征。这些机制均可以在很大程度上提高K-means的聚类速度[13-14]。
Elkan 等人[15]提出利用三角不等式提高K-means 聚类的速度,减少了K-means内部循环的计算。由于在通用的K-means 中,每个数据点和中心之间的距离被计算,并且每个数据点被分配到其最近的中心;而使用三角不等式,通过忽略来自某些中心的数据点的一些距离计算,保留一些额外信息来加速这个循环。当在数据规模不变且聚类数量增多的情况下,由于每个聚类可忽略的数据点减少,从而导致在提升聚类速度方面有所降低。
Lai 等人[16]提出一种过滤算法,利用中心变化来加速聚类过程。该算法将聚类划分为静态和动态两种,然后通过从动态聚类中心集中查找每个节点的候选者来降低计算复杂性。虽然使用了一种簇位移信息的技术排除K-D 树中所有节点不可能的聚类中心,但随着树中节点规模的增大,这种排除技术会影响整个聚类速度。
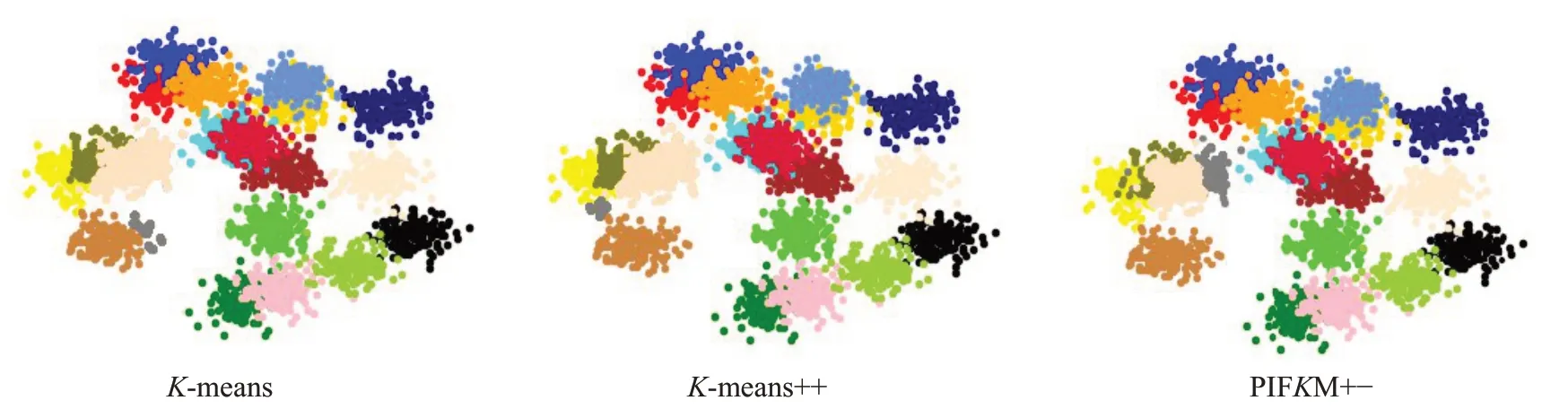
在聚类数量增多的情况下,以上方法都有一定的局限性,于是提出了一种局部迭代的快速K-means聚类算法PIFKM+−(Partial Iterative FastK-Means plus-minus)。该算法借鉴了I-K-means−+[17]算法的聚类分割和聚类删除的思想,优化了其算法,在已有聚类的基础上,在每次迭代过程中,首先依据聚类成本最大和聚类标签为可分割这两个条件选择能够被分割的聚类Si(+),然后依据聚类成本最小和聚类标签为可删除这两个条件选择能够被删除的聚类Sj(−),最后对这些聚类以及邻居聚类进行局部聚类更新,降低了算法的时间复杂度,提高了算法的执行效率和聚类的精确性。图1(a)展示的是K-means聚类效果,图1(b)展示的是PIFKM+−算法的聚类效果,把图(a)中圆圈部分进行了聚类分割,方形部分进行了聚类删除。
2 算法的相关定义
2.1 基本概念
在参考I-K-means−+的基础上,对文中用到的一些相关术语做出了定义。
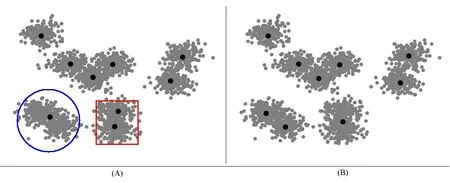
图1(a) K-means的聚类结果

图1(b) PIFKM+-的聚类结果
聚类的分割:当一个聚类簇Si中所有数据点到该聚类中心Ci的距离平方之和Cost(Si)很大,并且聚类簇Si没有被标记为不能分割时,从中任选一点作为第二个中心,然后围绕这两个中心重新聚类并更新Ci和,直到目标函数Cost(Si)和收敛为止,如图2所示。

图2(a) 分割之前的聚类簇
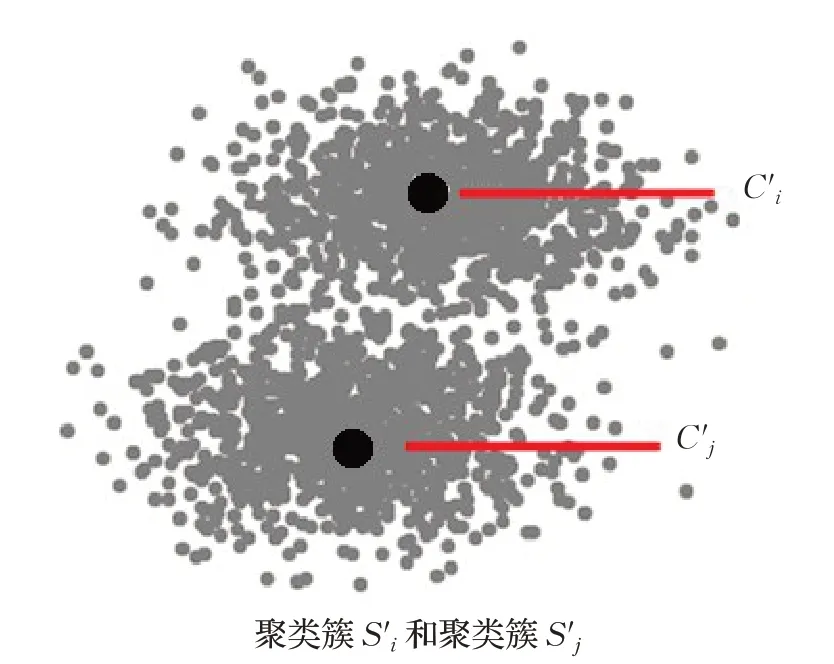
图2(b) 分割之后的聚类簇
聚类的删除:当一个聚类簇Sj的距离平方之和Cost(Sj)很小,并且没有被标识为不能删除,同时还存在一个强邻居Sk时,可以删除其聚类中心Cj并把Sj中的数据点合并到Sk里,然后再更新Sk的中心Ck,直到目标函数Cost(Sk)收敛为止,如图3所示。
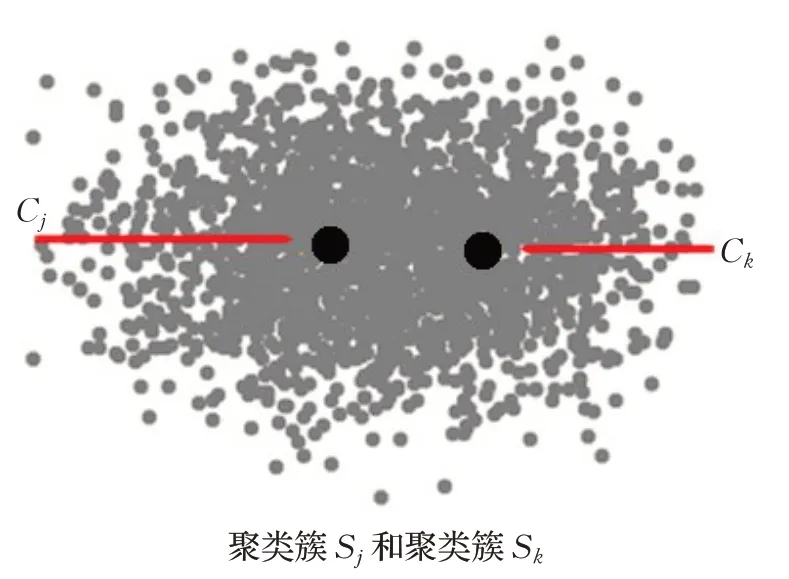
图3(a) 删除之前的聚类簇
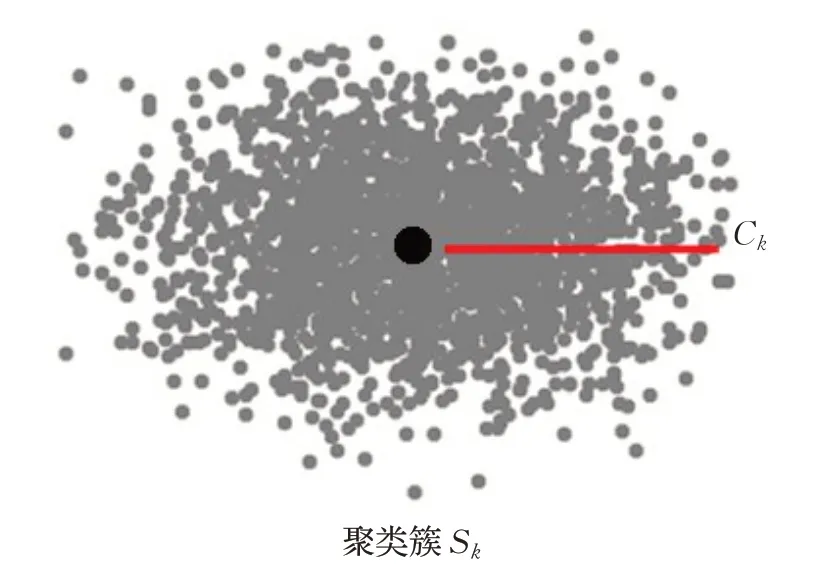
图3(b) 删除之后的聚类簇
聚类的邻居:聚类Si是聚类Sj的邻居,当且仅当聚类Sj中的数据点P,它的第一最近中心是Cj,而第二最近中心是Ci。
虽然聚类Si是聚类Sj的邻居,但反过来不一定成立,并且一个聚类可以有多个邻居。所以聚类的邻居是非对称的,是一对多的关系。
聚类的强邻居:两个聚类是强邻居关系,当且仅当两个聚类互为邻居。
如果一个聚类是在当前阶段通过分割其他聚类而得到的,那么在下次迭代过程中这个聚类以及它的强邻居都不能被删除。同理,如果一个聚类在当前阶段被删除,那么在下次迭代过程中,它的强邻居就不能被分割。
可能受影响的点:在局部聚类的过程中,当且仅当数据点P的第一或者第二最近中心是Ci时,数据点P才是聚类中心Ci的可能受影响点。
2.2 相关定义
在迭代过程中对两个聚类簇进行分割删除之前,必须找到合适的对象,才能使得PIFKM+−算法的聚类成本小于传统的K-means。文中算法均采用公式(1)作为统一的聚类成本函数。
定义1 用Cost-(Si)表示分割聚类簇Si所减少的聚类成本。如果聚类簇Si被分割成和两个聚类簇,那么Cost-(Si)就可以表示为聚类簇Si的成本减去和两个聚类簇的成本,即:

下面对Cost-(Si) 进行估算,由于Cost(Si) 是已知的,所以只需要计算两个值就可以得到Cost-(Si)的值。聚类簇Si中,每个数据点与聚类中心Ci的平均距离可以表示为:

其中,|Si|表示聚类簇Si中数据的个数。假设Si被分割之后,数据点被平均分配到两个新的聚类簇中,即:

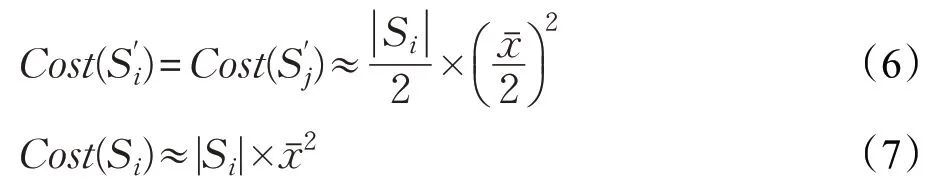
把公式(6)和(7)代入公式(3)得:
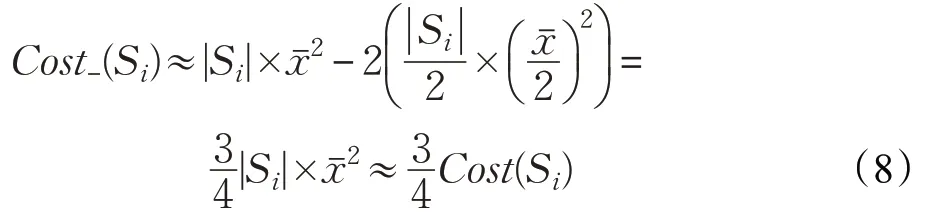
定义2 用Cost+(Sj)表示删除聚类簇Sj所增加的聚类成本。如果聚类簇Sj被删除,那么它的数据点会被合并到它的强邻居中。因此Cost+(Sj)可以近似表示为:
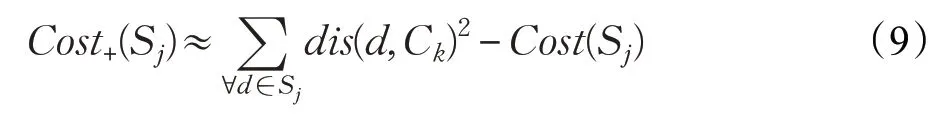
其中,Ck是聚类簇Sj中数据点的第二最近中心点。
推论在PIFKM+−算法的局部迭代聚类过程中,符合分割和删除条件的一对聚类簇,必须满足条件:

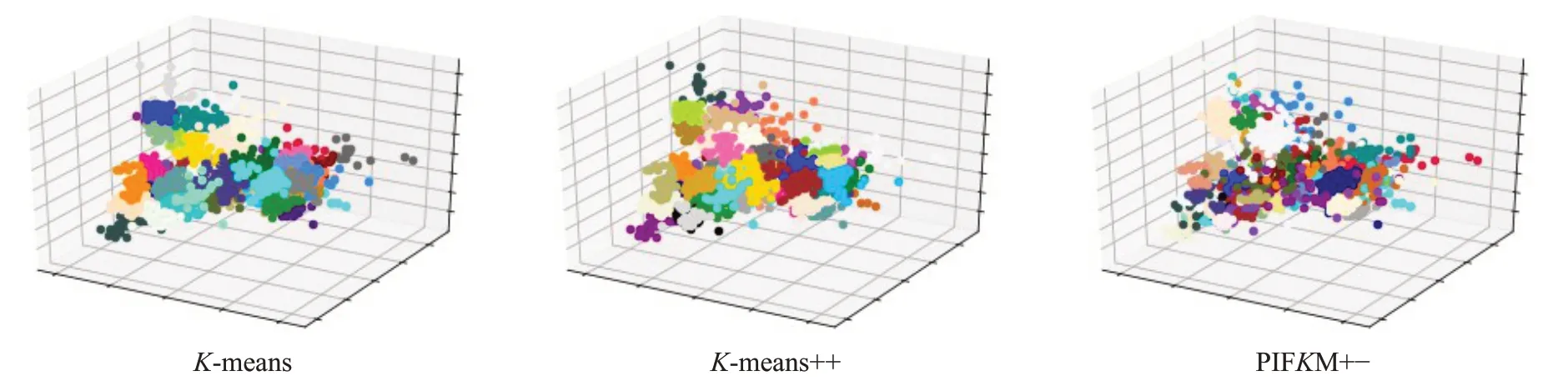
证明使Cost(S)表示K-means聚类的成本,Cost(S')表示经过聚类簇的分割删除之后的聚类成本。因为Si被分割之后,聚类成本减少了,而Sj被删除之后,聚类成本又增加了,所以Cost(S')=Cost(S)-Cost-(Si)+Cost+(Sj)。要使不等式Cost(S') PIFKM+−是在传统K-means 聚类[18-19]的基础上,通过一个局部迭代程序不断地寻找那些能够被分割的聚类簇和能够被删除的聚类簇,并对受影响的数据进行重新聚类处理的算法实现,目的是在聚类数量增多的情况下,降低算法的时间复杂度,进一步提高聚类的效率和聚类结果的精确度。如图4 给出了PIFKM+−算法的基本执行过程。 图4 PIFKM+−算法流程图 P-K-means 算法是传统K-means 的一种强化版本,仅适用于可能受影响的点。在PIFKM+−的聚类分割删除阶段中,只有一部分聚类簇被更改,因此P-K-means仅应用于整体解决方案的局部聚类。例如,在图5 中,PIFKM+−在聚类分割删除阶段,确定应该删除聚类簇S8,并且应该分割聚类簇S3。所谓删除S8,并没有真的删除,只是把中心C8的位置改变为聚类簇S3中的一个随机点。PIFKM+−算法通过只处理受影响的点并忽略其他未受影响的点来加速重新聚类过程。下面给出P-K-means算法在此例的基本执行过程。 图5 PIFKM+−的聚类分割删除阶段 假设算法已经找到了一对分割删除聚类簇S3和S8,并且知道S3将被分割,S8将被删除: 步骤1 定义集合AC、APc、APs和ADc,均初始化为空集。 步骤2ADc={C9}#C9为C8的强邻居聚类中心。 步骤3APc←C8被所在聚类受影响的数据点和ADc包含中心所在聚类受影响的数据点。 步骤4C8←取聚类簇S3中的一个随机数据点。 步骤5AC={C3}⋃{C8}。 步骤6APs←AC所有中心所在聚类受影响的数据点。 步骤7 通过集合APc包含的数据点,更新集合ADc包含的中心。 步骤8 通过集合APs包含的数据点,不断更新集合AC包含的中心,直到这些中心收敛为止。 步骤9 程序运行结束。 这一部分描述了PIFKM+−算法的完整执行过程,其中详细介绍了寻找分割删除聚类对的满足条件。 步骤1 应用K-means 算法对原有数据集进行聚类处理,得到聚类的成本Cost(S) 和聚类的解决方案S={S1,S2,…,Sk}以及各聚类中心。 步骤2 初始化计数变量count=0。 步骤3 在解决方案S中,选择Cost-(Si)最大的聚类簇Si,并且该簇没有被标记为不可分。如果没有符合条件的簇,程序结束。 步骤4 如果k2 以上聚类簇的Cost-(∗) 比Si的Cost-(Si)值大,程序结束。 步骤5 在解决方案S中,选择一个可以被删除的聚类簇Sj,需要满足以下条件: (1)Sj没有被标记为不可删除; (2)Si≠Sj; (3)Si和Sj不是强邻居; (4)Cost+(Sj)最小; (5)Cost-(Si)>Cost+(Sj)。 如果没有符合条件的簇,程序结束。 步骤6 如果k2 以上聚类簇的Cost+(∗) 比Sj的Cost+(Sj)值小,程序结束。 步骤7 应用P-K-means 算法执行聚类的分割删除操作,然后更新解决方案S,得到最新的解决方案S'。 步骤8 在解决方案S'中,标记聚类簇Si和Sj不能移除;把Sj之前的强邻居标记为不能分割。 步骤9 保存最新解决方案S=S'。 步骤10count=count+1。 步骤11 如果变量count值小于k2,跳转到步骤3。 步骤12 程序结束。 传统K-means 算法的聚类结果对于聚类中心初值的选择有很大的敏感性。如果聚类中心初值选择合适,其聚类成本较低,收敛性较好;反之,聚类成本较高,收敛性较差。而PIFKM+−算法是在传统的K-means 聚类结果的基础上,把那些能够被分割的聚类成本较大的聚类进行分割,把能够被删除的聚类成本很小的聚类进行删除(合并),最终使得聚类的总成本小于传统的K-means 聚类成本,从而达到进一步优化聚类效果,降低聚类总成本,提高聚类结果收敛性的效果。 为了验证PIFKM+−算法的聚类效果、高效率性和可行性,使用大规模仿真数据和真实数据进行了实验,同时对 PIFKM+−与K-means[20]、K-means++[21]两种算法在聚类效果和运行效率上进行了对比。所有的算法均采用Python3.6 编码实现,整个实验在Spyder 集成开发环境下进行测试,实验平台配置为双核i7处理器,8 GB内存,64位Windows 7操作系统。 实验使用的仿真数据集一共包含6组:Data1~Data6,通过Python 的scikit-learn 库生成。为了便于各种算法聚类效果的可视化,这6 组数据集包含的均是二维数据,区别在于不同的聚类个数和数据量。 真实数据集一共包含3 组,均来自UCI Machine Learning Repository 网站,具体地址 http://archive.ics.uci.edu/ml/datasets.html。测试数据集的详细信息描述如表1所示。 表1 实验数据集 如表2,列出了参与测试的算法在仿真数据集上所得到的运行结果。对于聚类最终成本Cost而言,PIFKM+−的聚类效果明显优于K-means 和K-means++两种算法。 对于各算法的运行时间,由于PIFKM+−算法是在K-means聚类的基础上进行进一步的优化处理,所以在全部的数据集上,PIFKM+−算法比K-means 算法的运行时间慢一些,但是在某些数据集上的运行时间要比K-means++算法快。为了进一步对3种算法进行评估,可以从簇内的稠密程度和簇间的离散程度来评估聚类的效果。在实验过程中采用了Calinski-Harabasz(CH)[19]指标,该指标值越大说明聚类效果越好,如表3所示。 实验结果表明,PIFKM+−算法的聚类效果完全优于K-means和K-means++的聚类效果。PIFKM+−可以在损失较小速度的情况下提高聚类的效果,降低了聚类的成本。图6~11显示了各种算法在6组仿真数据集上的聚类效果。 表2 在仿真数据集上聚类总成本和聚类总时间 表3 在仿真数据集上Calinski-Harabasz(CH)指标统计结果 图6 Data1上3种算法的聚类结果 图7 Data2上3种算法的聚类结果 图8 Data3上3种算法的聚类结果 图9 Data4上3种算法的聚类结果 图10 Data5上3种算法的聚类结果 图11 Data6上3种算法的聚类结果 如表4,列出了PIFKM+−算法以及参与测试比较的K-means和K-means++算法在3组真实数据集上所得到的运行结果,包含了聚类总成本、聚类总时间以及相应的比值。PIFKM+−算法的平均运行时间是K-means算法的1.35 倍;PIFKM+−算法的平均聚类成本是K-means 算法的0.94 倍。而与K-means++算法相比,PIFKM+−算法的平均运行时间是K-means++算法的1.07 倍;PIFKM+−算法的平均聚类成本是K-means++算法的0.96 倍。经过以上统计分析,表明了PIFKM+−算法可以在损失较小速度的情况下进一步提高聚类的效果。 如表5是通过Calinski-Harabasz(CH)[19]指标对参与比较测试的3种算法进行聚类效果的评估,指标值越大说明聚类效果越好。从实验结果可看出,PIFKM+−算法在 Letter-Recognition 和 Anuran Calls(MFCCs)两个数据集上的聚类效果与K-means 和K-means++算法相比,分别平均提高12.5%和9%。这说明对于聚类数量增多的数据集,PIFKM+−算法的聚类性能优于传统的K-means算法。 表4 在真实数据集上聚类总成本和聚类总时间 表5 在真实数据集上Calinski-Harabasz(CH)指标统计结果 图12 Letter-Recognition上3种算法的聚类结果 图13 Wholesale Customers上3种算法的聚类结果 图14 MFCCs上3种算法的聚类结果 由于3 组真实数据的维数很大不能直接展示聚类效果,为了更好地展示真实数据的聚类效果,实验过程中先通过主成分分析方法(PCA)对3 组真实数据进行了降维处理再聚类,经过实验对比发现三维聚类效果要略优于二维聚类效果,如图12~14展示的是各种算法在真实数据集上三维空间的聚类效果。 为了解决K-means 算法在聚类数量增多的情况下因不能选择合适的聚类中心初值而影响聚类效果这一问题,提出了一种局部迭代的快速K-means 聚类算法(PIFKM+−)。该算法在K-means聚类的基础上,不断地寻找能够被分割和能够被删除的聚类簇,并对受影响的局部数据进行重新聚类处理以此提高聚类的效果。PIFKM+−算法在面对聚类数量众多的情况下,具有能够快速更新聚类、对聚类中心初值不敏感并能够提高聚类精确度等优势。下一步的工作重点有两个:一是如何快速寻找能够被分割和删除的聚类对;二是如何加快对局部聚类的更新处理,从而进一步提高聚类的速度和效果。 致谢感谢教育部《高等学校青年骨干教师国内访问学者项目》所提供的在天津大学访学的机会,感谢天津大学智能与计算学部的廖士中教授对我研究工作的指导和帮助。3 PIFKM+-算法
3.1 算法思想

3.2 P-K-means算法
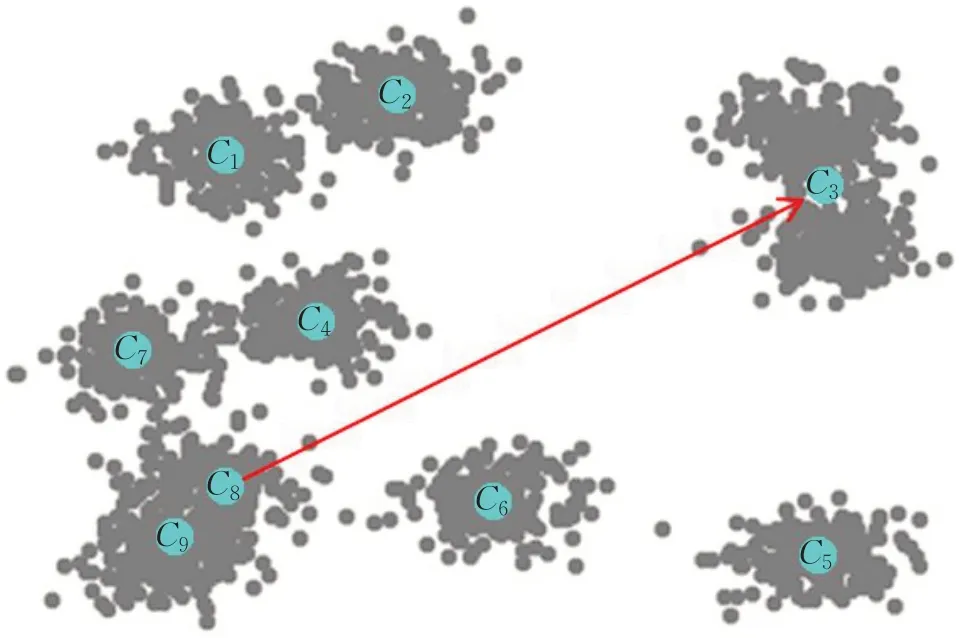
3.3 PIFKM+−执行过程
3.4 PIFKM+−与传统K-mean的性能比较
4 实验测试及结果分析
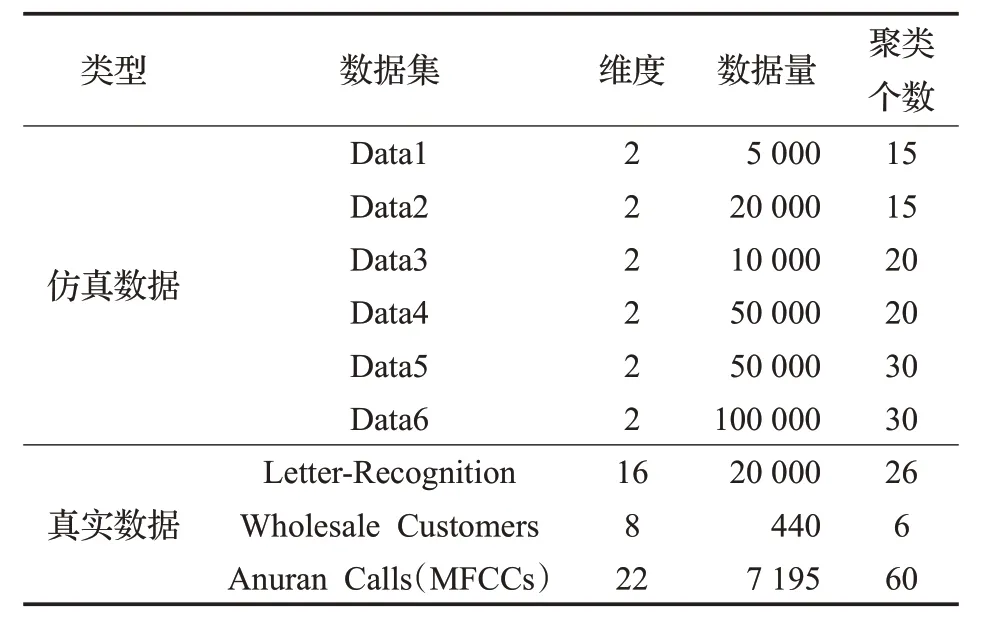
4.1 仿真数据集测试结果







4.2 真实数据集测试结果




5 结论
