考虑抗弯刚度的耦合吊索自振特性研究
2020-07-06陈炜王荣辉周浩恩甄晓霞张卓杰
陈炜 王荣辉 周浩恩 甄晓霞† 张卓杰
(1.华南理工大学 土木与交通学院,广东 广州 510640;2.中交隧道工程局有限公司华南分公司,广东 广州 510700;3.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043)
随着悬索桥跨度的增大,吊索在交通荷载及环境激励下容易产生较大的振动,如果吊索振动得不到消除或控制,很容易引起索的疲劳破坏及套筒保护层的破坏,甚至导致桥梁的破坏[1- 2]。为了有效地控制吊索的振动,通常把同一吊点的多根索股用减振架连接起来[3],从而形成一个协同工作系统,系统内各根索间的耦合作用导致吊索的自振特性与单根索股不同,分析时须进行简化或等效。
文献[4- 5]将带减振架的吊索简化为不同约束与荷载作用下的单根吊索受力模型,但悬索桥吊索实际上是在内部节点耦合下的多索股系统,其振动是各索股相互作用的综合体现,与单根索股或完整性良好拉索的振动行为不一样。
文献[6- 8]对通过耦合连接的双层及多层索网进行了初步的自振特性分析;文献[9- 10]对通过耦合连接的索网和外置阻尼器混合索网系统的自振特性进行了进一步分析;文献[11- 12]将拉索-弹簧-阻尼器系统模型用于斜拉桥的辅助索减振机理分析;文献[13]通过环境激励法确定了吊索的动力特性及分隔器减振方案,并对分隔器减振效果进行了对比研究;文献[14]考虑双索股吊索的面内振动,推导了双索股之间安装阻尼器时的运动微分方程;文献[15]建立了带减振架吊杆的运动微分方程,明确了减振架刚度、吊杆索力及其振动频率间的关系;文献[16- 18]建立了两拉索-弹簧-阻尼系统模型,分析了系统自由振动的频率及阻尼特性。文献[6- 18]的理论研究未考虑索的抗弯刚度,由于悬索桥吊索相对于斜拉索等其他索结构而言长度较短、刚度相对较大,抗弯刚度影响的比重较大,如果对耦合后的索股系统自振特性进行计算时忽略抗弯刚度的影响,会使理论公式计算得到的索自振频率小于实际值,这将导致与实际情况有所差别,因此在研究耦合吊索自振特性时,有必要考虑吊索的抗弯刚度。
本研究提出了考虑索抗弯刚度的双索股耦合系统模型,推导了吊索振动的理论公式;对吊索自振频率进行求解后使用试验及数值分析方法对该理论公式进行验证;另外,还研究了索的抗弯刚度、减振架耦合位置、耦合刚度、索的长度与索的振动频率和模态振型之间的关系;以期为研究减振架减振机理提供依据。
1 吊索耦合振动模型建立
本研究以矮寨大桥为例来展示把同一吊点的多根索股用减振架连接起来而形成的协同工作系统,矮寨大桥吊索及减振架布置图如图1所示,矮寨大桥典型吊索构造图如图2所示。

图1 矮寨大桥吊索及减振架布置图
Fig.1 Layout of suspenders and anti-vibration mount of Aizhai Bridge
悬索桥主缆上同一吊点位置通常有2根、4根或6根索股,吊索与索夹为骑跨式连接,横桥向2根 索股顶端通过索夹连接,底端通过锚头锚固在加劲梁上,索股间设置减振架。可将索股等效为横桥向两根由弹簧连接的弦,索端固定,从而带减振架的吊索系统均可简化为图3所示的模型,索间连接方式可根据减振架刚度等效为刚性耦合和弹性耦合两类。基于此模型可求解吊索系统的振动方程。图3中T1、T2分别为左右索所受的拉力,索股总长为L,分段索长分别为l1、l2,建立坐标系x1o1y1、x2o2y2。
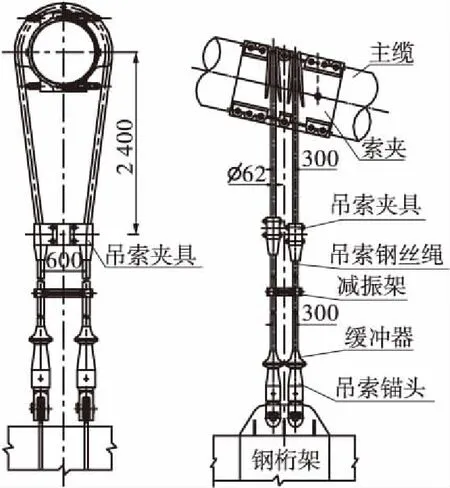
图 2 矮寨大桥典型吊索构造图(单位:mm)
Fig.2 Structural layout of typical suspender of Aizhai Bridge(Unit:mm)
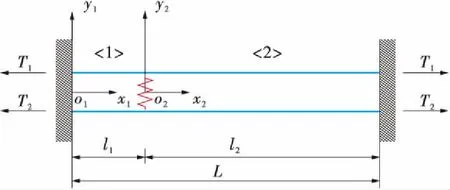
图3 双索股耦合系统模型
任意外力作用下各索股的横向振动的微分方程可表示为[19]
(1)
式中:v(x,t)为拉索横向位移;x为沿拉索轴线的坐标;t为振动时间;E为拉索弹性模量;I为拉索横截面对中心主轴的惯性矩;T为拉索拉力;m为拉索的单位长度质量。
式(1)可采用分离变量法求解,设方程解的形式为
v(x,t)=φ(x)q(t)
(2)
其中:φ(x)为关于x的函数,q(t)为关于t的函数。把式(2)代入式(1),两边同除mφ(x)q(t),得到等号两边不同变量的等式,由于两个变量x、t没有相关性,可得:
(3)
对式(3)进行分离变量后,可以转换为以下两个方程式:
(4)
(5)
式中,ω为圆频率。
式(5)为四阶齐次线性常微分方程,其解为
φ(x)=Acos(αx)+Bsin(αx)+
Ccosh(βx)+Dsinh(βx)
(6)
其中
(7)
(8)
式(4)的解为
q(t)=Ecos(ωt)+Fsin(ωt)
(9)
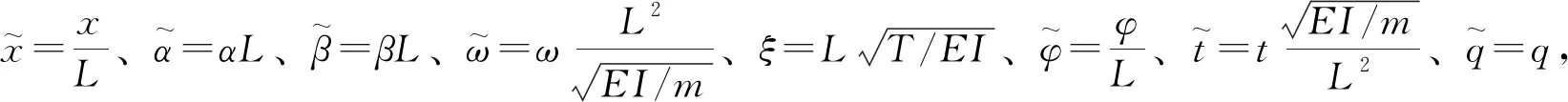
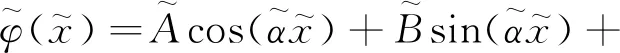

(10)
其中
(11)
(12)
对式(9)进行无量纲化得
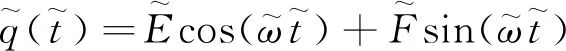
(13)
故得
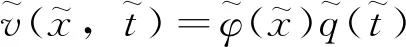
(14)
在各子系统内,各索股振动方程的解形式如下:
(15)
式中:i表示索股号,i=1,2;j表示子系统号,j=1,2。
由于各索股通过耦合形成整体,故各索股的振动频率相等,即
(16)
因此,只需求解各索股的振型方程即可,
(17)
2 方程求解
对于双索股单节点耦合系统,式(17)为含有16个待定系数的联立方程组,其解可通过边界条件、连续性要求及竖向力平衡要求确定。
2.1 边界条件
由于索股两端固结,索股端部的位移、斜率均为零,即
(18)
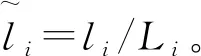
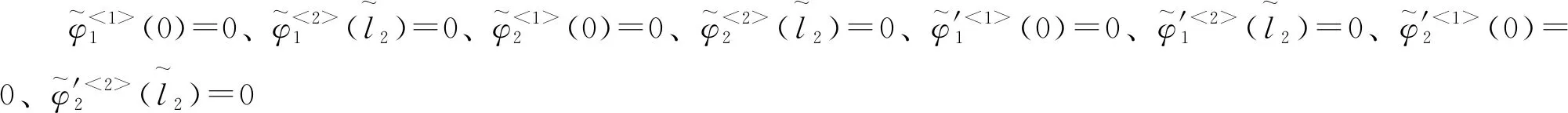
2.2 连续性要求
由于对同一索股的耦合作用可等效为一作用力,因此考虑抗弯刚度的同一索股在耦合处的位移、斜率、弯矩不会发生突变,因此同一索股在耦合处两端的位移、斜率、弯矩相等,即
(19)
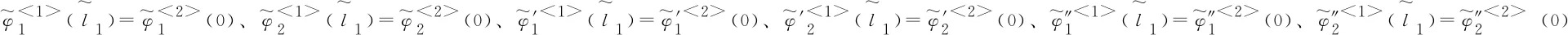
2.3 竖向力平衡要求
由于同一索股在耦合处只受到耦合变形对它的作用力,此作用力与索股耦合处两端的剪力差相等,即
(20)
共有2个方程。
2.4 频率求解
上述得到的16个方程,写成矩阵形式为
KX=0
(21)
式中:K为16×16的系数矩阵;X为16×1的待定系数列向量,其中
若式(21)有解,则系数矩阵行列式为零,即
det(K)=0
(22)
2.5 不考虑抗弯刚度的频率方程
另外,若将单根索股看作完整性良好的柔性弦,系统索力T和基频f1之间的关系可表示为
(23)
式中,m为拉索的线密度,L为拉索长度。
对悬索桥,若同一吊点的各根索股索力及线密度、索长均相同,即
T=T1=T2,
m=m1=m2,
不考虑索的抗弯刚度时,频率方程可简化为
βTsin2(βL)+2ksin(βl1)sin(βl2)sin(βL)=0
(24)
式中:L为整根索股的长度;l1、l2为被耦合点分开的两段索股的长度。
式(24)中k在两种极限状态下的解族分别对应索股间无耦合作用及带刚性减振架的自由振动:
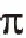
(2)k→时,sin(βL)=0,sin(βli)=0(i=1,2)的两组解族为βL=n和βli=n,即f=nf1和分别对应索的整体振动与附加振动。
3 理论推导正确性验证
通过现场试验对理论推导公式进行验证。图4所示为两根张拉着一定拉力值的钢绞线独立锚固在自制的受力架上组成的双索股单索夹系统,各索股的长度L均为3.37 m,在距离索股左端L/10处用带有一定刚度的索夹进行连接,即l1=0.337 m,l2=3.033 m。索股的拉力存在10%的偏差,即索股的拉力T1=31.5 N,T2=28.5 N,试验索股参数如表1所示。

图4 现场试验装置图

表1 试验索股参数
索股的拉力由配套着油压表的千斤顶进行施加后,再通过旋转索股右侧的螺母对拉力值进行细调,拉力值可通过图5(a)所示的压力传感器测得并由连接着压力传感器的静态应变测试系统读出。索间耦合连接可通过图5(b)、5(c)所示的不同刚度的索夹进行模拟,索夹的刚度在实验前通过压力试验机测出,分别为k1=107N/m、k2=104N/m。张拉完成后,在每根索股各布置两个加速度传感器来收集索股的振动数据,并通过连接着加速度传感器的动态应变测试系统显示的频谱图读取自振频率,图6所示为两索股单索夹系统的频谱图。各个传感器读取的自振频率均一样。
利用有限元软件ANSYS建立考虑拉索抗弯刚度的两索股单节点耦合拉索模型,其中拉索采用Beam188单元模拟,单元参数按表1进行设置,并且拉索拉力用预拉力的方式进行施加,节点耦合采用Combin14单元模拟。

(a)压力传感器

(b)索夹k1=107 N/m

(c)索夹k2=104 N/m
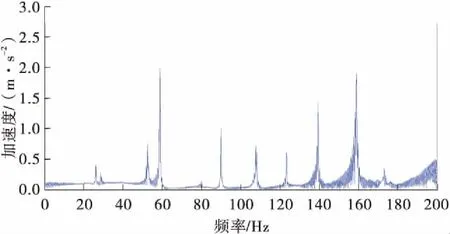
图6 两索股单索夹系统频谱图(k=107 N/m)
Fig.6 Spectrogram of two strands system with single cross-link(k=107N/m)
由本文算法、有限元算法及试验得到的索股系统前十阶自振频率分别如表2中的fS1、fS2、fS3所示,表中s1、s2分别为fS1与fS2、fS1与fS3的相对误差。
由表2可见,当索夹刚度k=107N/m时,本文方法与有限元方法最大误差为0.13%,与试验实测结果最大误差为-2.01%;当索夹刚度k=104N/m 时,本文方法与有限元方法最大误差为0.13%,与试验实测结果最大误差为-6.21%;由此可以验证理论推导的正确性。
4 带减振架的吊索自振特性研究
为研究减振架对吊索振动特性的影响,以矮寨特大悬索桥C21L号索(总索长39.841 m,计算长度LA=17.7 m)、C12L号索(总索长89.53 m,计算长度LB=42.048 m)、C03L号索(总索长163.758 m,计算长度LC=79.176 m)为例进行算例分析,主缆上同一吊点有4根索股,吊索与索夹为骑跨式连接,索股在中点位置用减振架连接,吊索索力T1=T2=1 000 kN,分析模型如图3所示,相关参数值如表3所示。

表3 索股参数
4.1 索股抗弯刚度对吊索振动特性的影响
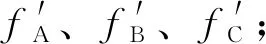
由图7可知:当刚性减振架位于L/2位置时,若不考虑索的抗弯刚度,因单根索股所受拉力与各结构参数均相同,以f1表示单根索股自由振动时的基频,吊索的自振频率值均为基频的整数倍(即为nf1,其中n是整数);吊索的频率分布曲线呈“阶梯状”,每4阶为一个变化周期,每个变化周期内第1阶对应同相整体振动模态,第2、3阶对应单根索单独振动模态,第4阶对应反相整体振动模态,第2、3、4阶频率值相等;考虑索的抗弯刚度后,频率分布曲线也呈现每4阶一个变化周期的阶梯状,但是反相整体振动频率比单根索单独振动频率大。随着减振架刚度减小,同相整体振动和单根索单独振动的频率不变,反相整体振动的频率值减小,趋近于前一阶同相整体振动模态的频率值。
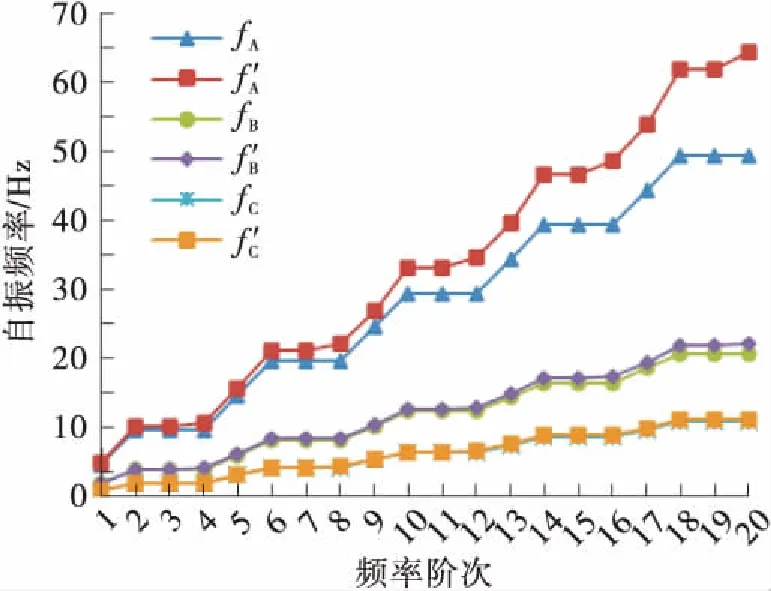
(a) k=∞
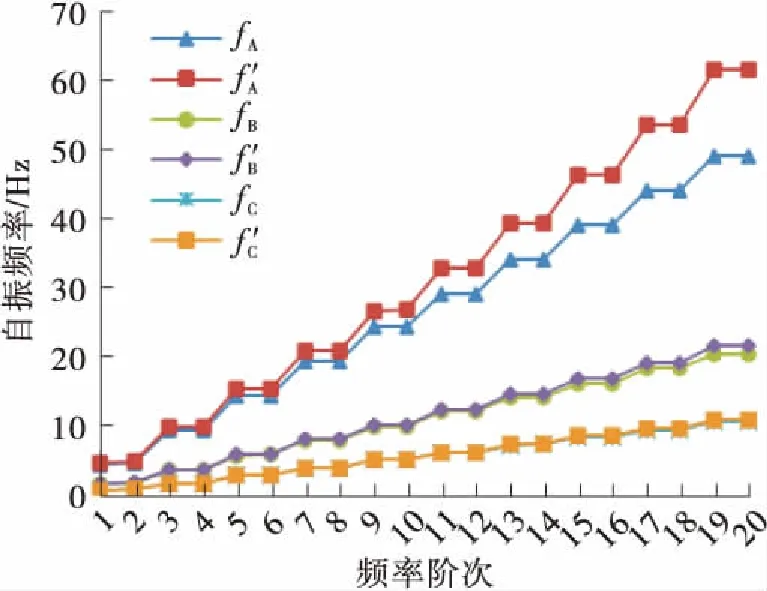
(b)k=104 N/m
Fig.7 First 20th order natural frequencies of the suspenders(the anti-vibration mount atL/2 position)
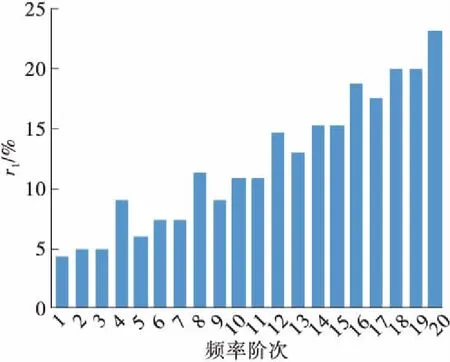
(a) C21L(k=∞)
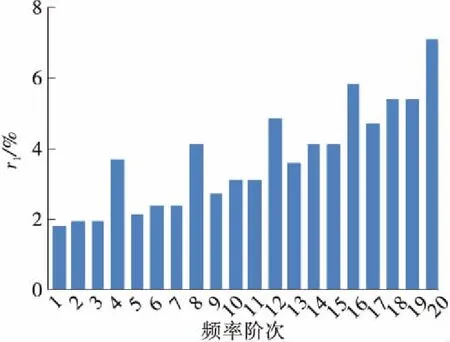
(b) C12L(k=∞)
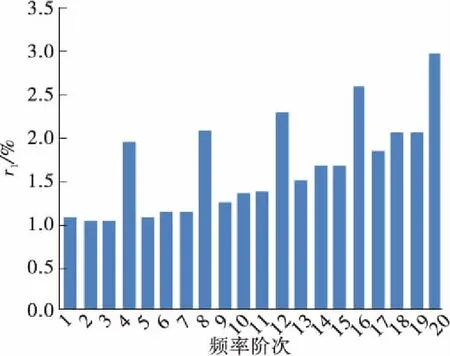
(c) C03L(k=∞)
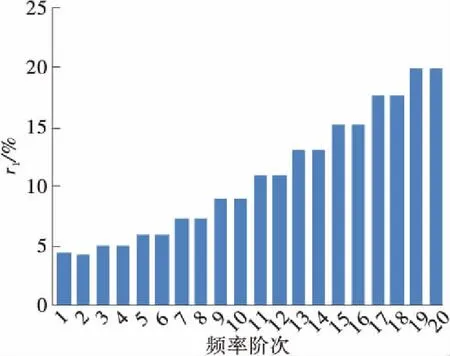
(d) C21L(k=104 N/m)
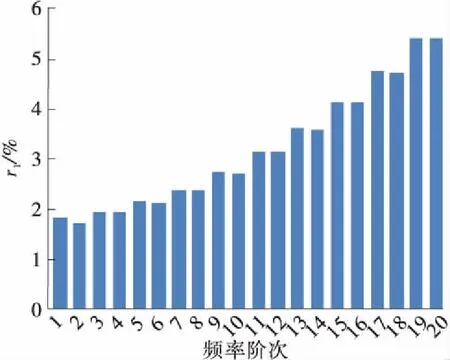
(e) C12L(k=104 N/m)
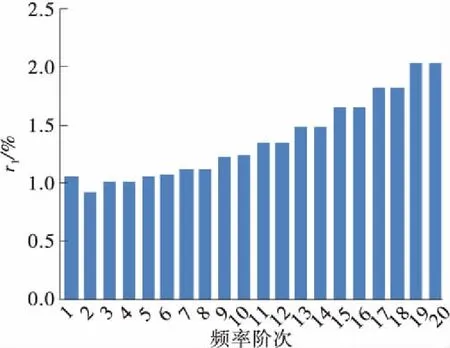
(f) C03L(k=104 N/m)
图8 考虑抗弯刚度后吊索前20阶自振频率的增长百分比(减振架位于L/2位置)
Fig.8 Increasing percentage of the first 20th order natural frequencies of the suspenders after considering bending stiffness (the anti-vibration mount atL/2 position)
由图8可知:索的抗弯刚度会对吊索的自振频率产生影响,索越短,考虑抗弯刚度后索的自振频率值增大越明显,随着索长增加,r1值逐渐减小;设置刚性减振架时,考虑抗弯刚度后C21L、C12L、C03L的r1最大值分别达到23.44%、7.12%、2.98%;减振架刚度为k=104N/m时,C21L、C12L、C03L的r1最大值分别达到20.11%、5.42%、2.05%。由于减振架刚度只影响反相整体振动的频率,而反相整体振动频率随着减振架刚度减小而减小,因此r1值随减振架刚度减小而减小。
4.2 减振架对吊索振动特性的影响
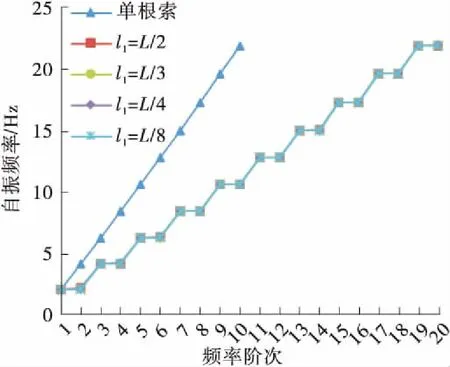
取减振架刚度k≥104N/m的情况进行研究,图9所示为减振架刚度k=∞与k=104N/m时C21L、C12L、C03L号吊索的前20阶自振频率随减振架位置的变化规律,图10所示为单根索股前5阶振型图与在L/2、L/4位置处设置减振架的C03L号吊索的前5阶振型图。
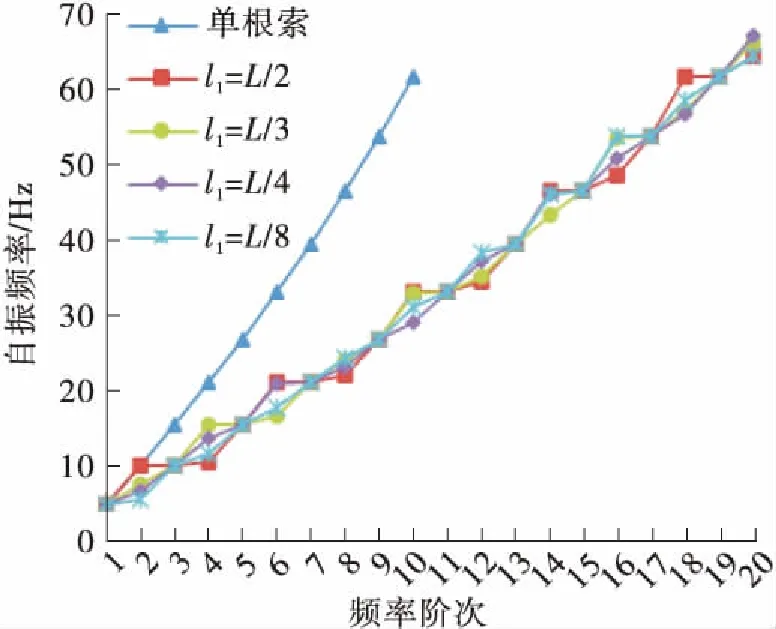
(a) C21L(k=∞)
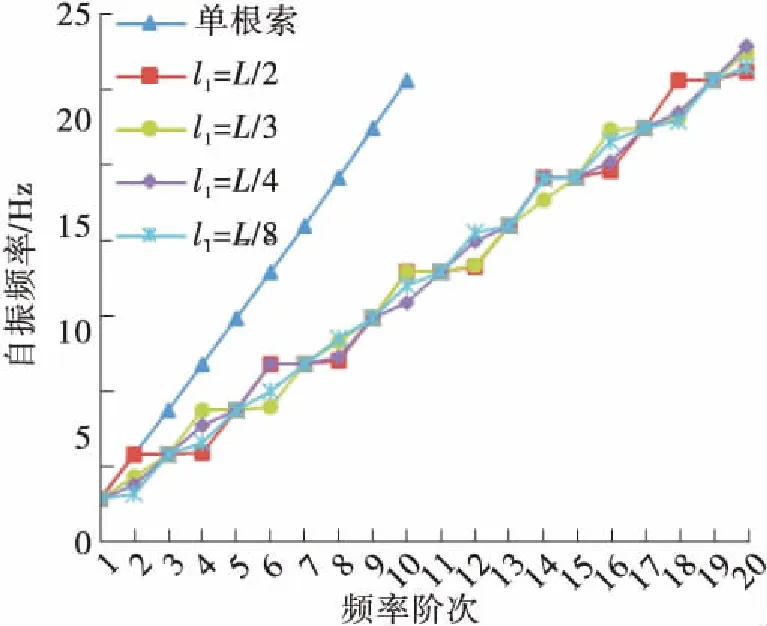
(b) C12L (k=∞)
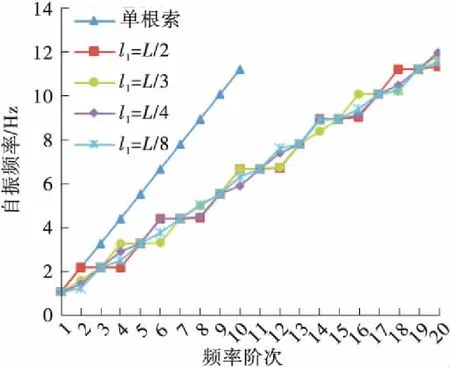
(c) C03L(k=∞)
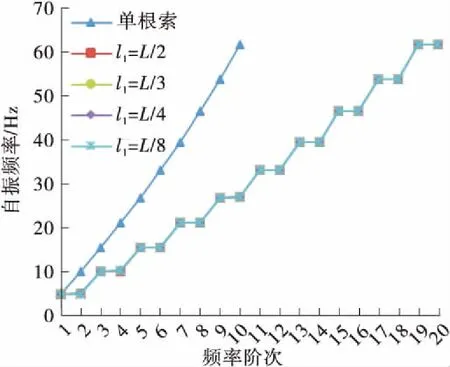
(d) C21L(k=104 N/m)
(e) C12L (k=104 N/m)
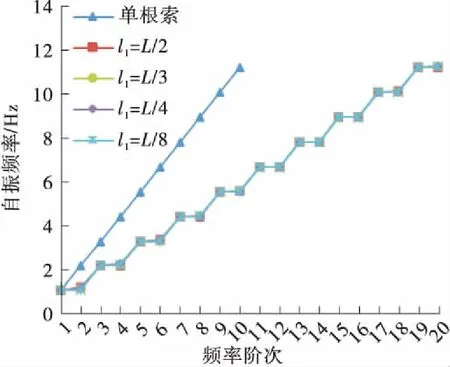
(f) C03L(k=104 N/m)
Fig.9 Curve of the first 20th order natural frequencies of the suspenders changing with the position of anti-vibration mount

(a) 单根索
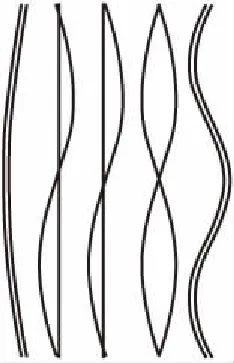
(b) l1=L/2(k=∞)
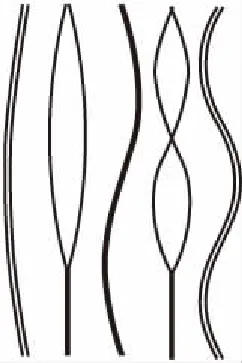
(c) l1=L/4(k=∞)
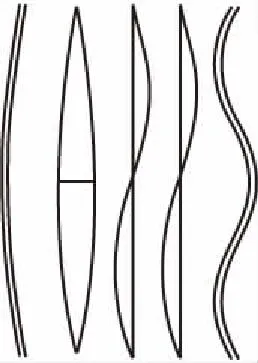
(d) l1=L/2(k=104 N/m)
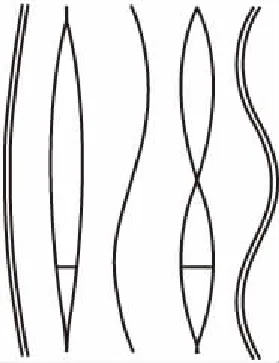
(e) l1=L/4(k=104 N/m)
由图9及图10可知,除减振架在吊索L/2位置处外,设置减振架后吊索的奇数阶振动模态为同相整体振动模态,其自振频率及振型与单根索股相应的自振频率及振型一致,减振架保证了多根吊索同相整体振动模态的一致性,减振架刚度对吊索同相整体振动模态的自振频率值无影响;吊索的偶数阶振动模态为设置减振架引起的反相振动模态,其自振频率、振型均受到减振架位置及刚度的影响。
不考虑索的抗弯刚度时,吊索同相整体振动模态的频率值呈整数倍增长;考虑索的抗弯刚度后,同相整体振动模态下各阶频率不再为基频的整数倍,索越短,其整体振动的频率值增长越快,随着索长增加,其整体振动的频率值接近似整数倍增长。
以r2表示减振架在不同位置时吊索的自振频率与减振架在L/2处时的差值百分比,吊索的反相振动频率值与减振架位置相关,设置刚性减振架的工况下,l1=L/8时C03L号吊索的最大r2值达到42.95%;随着减振架刚度减小,减振架位置对频率的影响也逐渐减小,k=104N/m时最大r2值为10.44%。
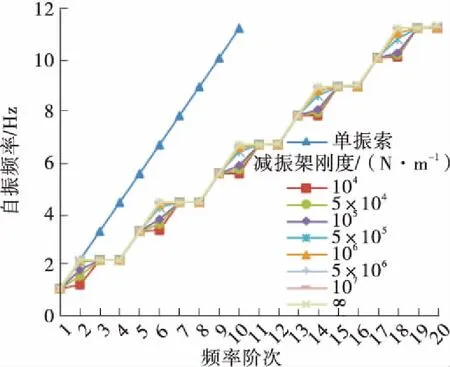
进一步分析减振架刚度对吊索自振频率的影响,l1=L/2、L/4、L/8时C21L、C12L、C03L号吊索前20阶自振频率随减振架刚度的变化情况如图11所示。
由图10(b)、10(d)和图11可知,当减振架位于L/2位置处时,频率分布曲线呈现为每4阶一个变化周期的阶梯状,同相整体振动和单根索单独振动的频率不会随着减振架刚度的变化而改变,而反相整体振动的频率随着减振架刚度的减小而减小。当减振架刚度k≤106N/m时,出现“跳阶”现象,第2阶振型表现为反相整体振动模态,其频率值随着减振架刚度的减小趋近于第1阶同相整体振动模态的频率值,第4阶振型表现为单根索单独振动模态。
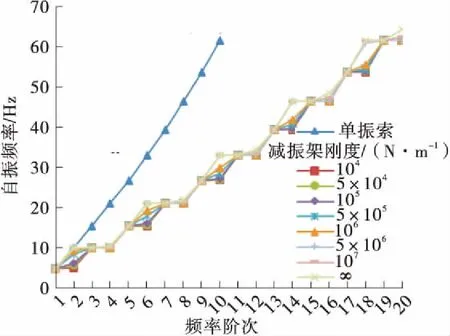
(a) l1=L/2,C21L号吊索
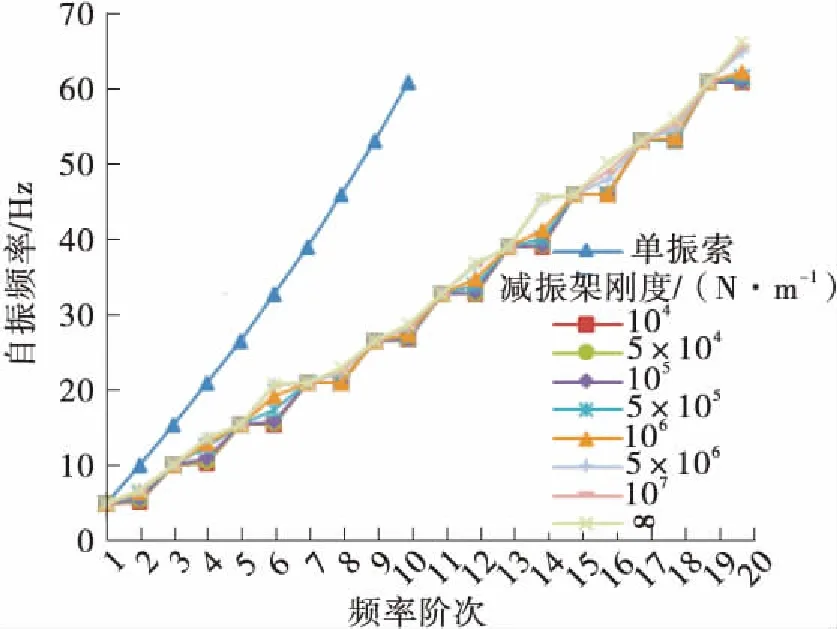
(b) l1=L/4,C21L号吊索
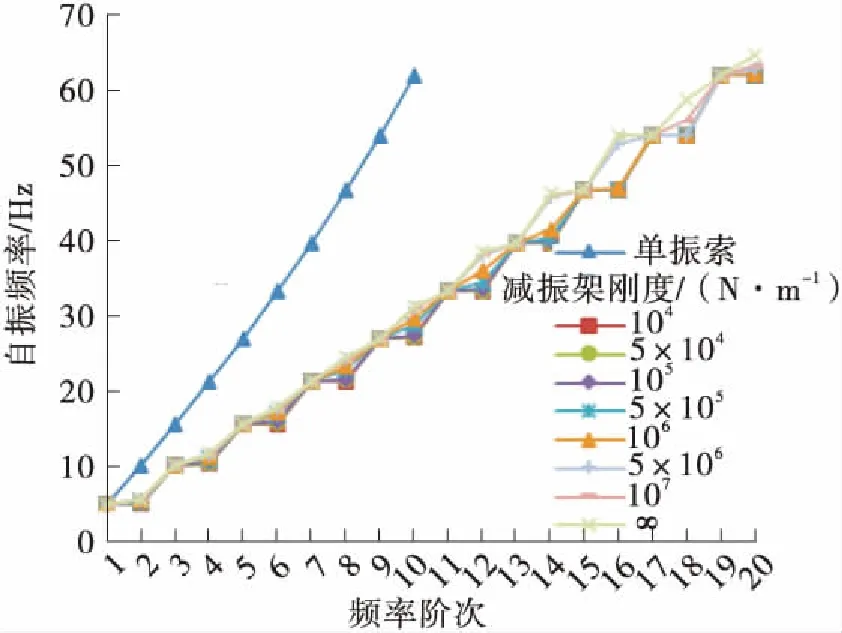
(c) l1=L/8,C21L号吊索
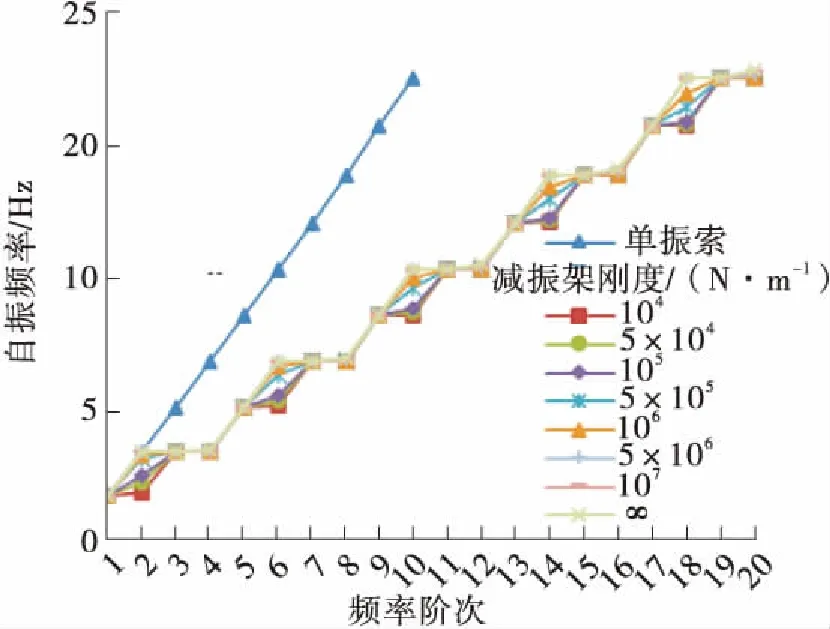
(d)l1=L/2,C12L号吊索
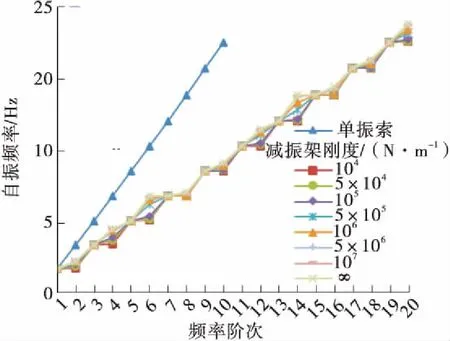
(e)l1=L/4,C12L号吊索
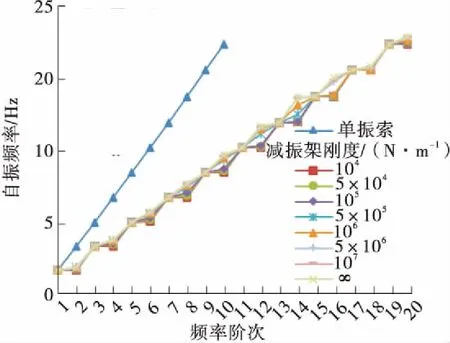
(f)l1=L/8,C12L号吊索
(g)l1=L/2,C03L号吊索
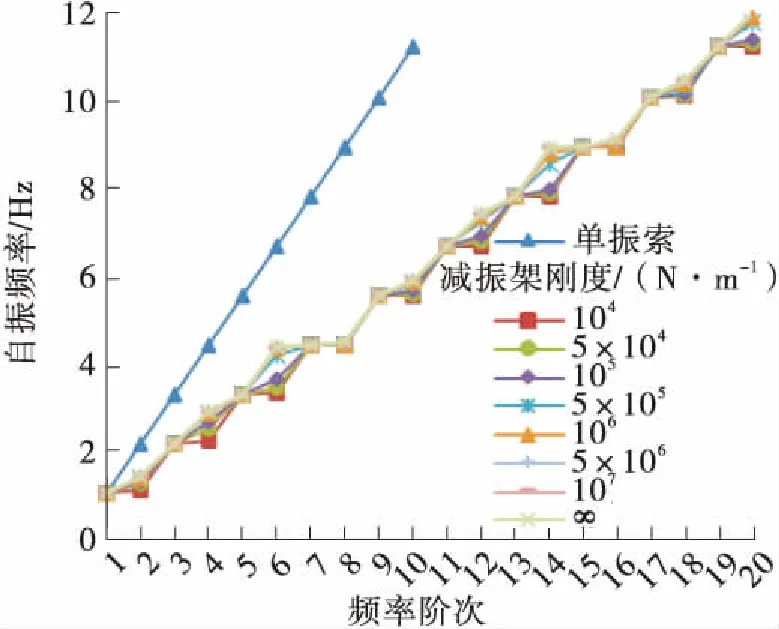
(h)l1=L/4,C03L号吊索
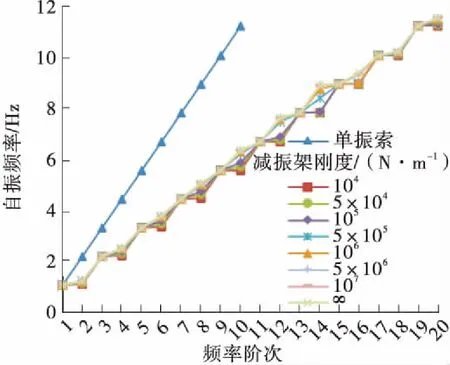
(i)l1=L/8,C03L号吊索
Fig.11 Curve of the first 20th order natural frequencies of the suspenders changing with the rigidity of anti-vibration mount
以r3表示减振架刚度不同时吊索的自振频率与减振架刚度为无穷大时的差值百分比,由图10-11可知,减振架刚度对反相振动模态的自振频率值有影响,减振架位置一定时,其刚度越小,r3值越大,并且减振架的约束减弱,造成局部振动的节点越不明显。
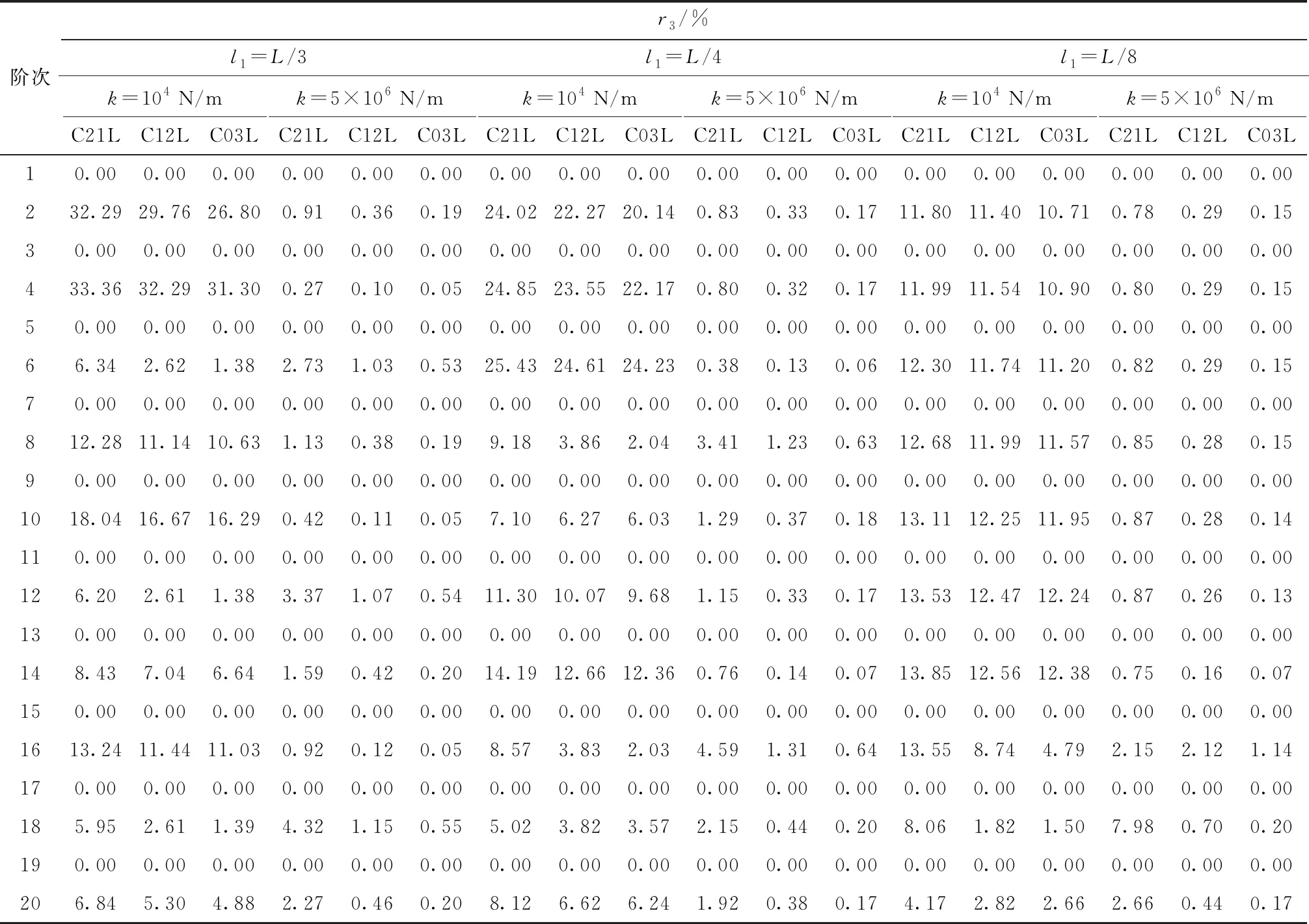
当减振架在L/3、L/4、L/8位置处,减振架刚度分别为k=104N/m、k=5×106N/m时跟减振架刚度为无穷大时吊索前20阶自振频率的差值百分比(r3)如表4所示。
从表4可以看出,对于不同长度的吊索,减振振架的刚度及相对位置一定时,r3值随着索长增长而减小;随着减振架刚度增大,r3值随索长增长而减小的相对幅度增大。如在k=104N/m的工况下,减振架位于L/3位置处时C21L、C12L、C03L号吊索的r3最大值分别为33.36%、32.29%、31.30%,减振架位于L/4位置处时C21L、C12L、C03L号吊索的r3最大值分别为25.43%、24.61%、24.23%,减振架位于L/8位置处时C21L、C12L、C03L号吊索的r3最大值分别为13.85%、12.56%、12.38%。在k=5×106N/m的工况下,减振架位于L/3位置处时C21L、C12L、C03L号吊索的r3最大值分别为4.32%、1.15%、0.55%,减振架位于L/4位置处时C21L、C12L、C03L号吊索的r3最大值分别为4.59%、1.31%、0.64%,减振架位于L/8位置处时C21L、C12L、C03L号吊索的r3最大值分别为7.98%、2.12%、1.14%。
表4 特定减振架刚度下吊索前20阶自振频率与减振架刚度为无穷大时的差值百分比
Table 4 Increasing percentage of the first 20th order natural frequencies of the suspenders between certain rigidity and infinite rigidity of anti-vibration mount
阶次r3/%l1=L/3l1=L/4l1=L/8 k=104N/m k=5×106N/m k=104N/m k=5×106N/m k=104N/m k=5×106N/m C21LC12LC03LC21LC12LC03LC21LC12LC03LC21LC12LC03LC21LC12LC03LC21LC12LC03L10.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.00232.2929.7626.800.910.360.1924.0222.2720.140.830.330.1711.8011.4010.710.780.290.1530.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.00433.3632.2931.300.270.100.0524.8523.5522.170.800.320.1711.9911.5410.900.800.290.1550.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.0066.342.621.382.731.030.5325.4324.6124.230.380.130.0612.3011.7411.200.820.290.1570.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.00812.2811.1410.631.130.380.199.183.862.043.411.230.6312.6811.9911.570.850.280.1590.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.001018.0416.6716.290.420.110.057.106.276.031.290.370.1813.1112.2511.950.870.280.14110.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.00126.202.611.383.371.070.5411.3010.079.681.150.330.1713.5312.4712.240.870.260.13130.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.00148.437.046.641.590.420.2014.1912.6612.360.760.140.0713.8512.5612.380.750.160.07150.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.001613.2411.4411.030.920.120.058.573.832.034.591.310.6413.558.744.792.152.121.14170.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.00185.952.611.394.321.150.555.023.823.572.150.440.208.061.821.507.980.700.20190.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.00206.845.304.882.270.460.208.126.626.241.920.380.174.172.822.662.660.440.17
此外,由于实际工程频率法测量索力时低阶较为明显,在k=5×106N/m的工况下,减振架位于L/3位置处时C21L、C12L、C03L号吊索的二阶r3值分别为0.91%、0.36%、0.19%,减振架位于L/4位置处时C21L、C12L、C03L号吊索的二阶r3值分别为0.83%、0.33%、0.17%,减振架位于L/8位置处时C21L、C12L、C03L号吊索的二阶r3值分别为0.78%、0.29%、0.15%,二阶r3值均小于1%,且前二十阶r3值绝大部分少于5%。因此,对于不同长度的吊索,当设置的减振架刚度k≥5×106N/m时,均可近似视为刚性减振架。
5 结论
本研究提出了考虑抗弯刚度的双索股耦合系统模型,并基于该模型对悬索桥吊索的自振特性进行研究,研究结果表明:
(1)设置减振架后,各根索股的自振频率均相同,减振架可保证两根索股同相整体振动模态的一致性,同相整体振动模态的自振频率值不受减振架影响;在同相整体振动模态之间存在单根索股单独振动模态(减振架位于吊索中点时成对出现)及反相振动模态,反相振动模态的频率值、振型均受减振架位置及刚度影响。
(2)考虑索的抗弯刚度后,带减振架的吊索自振频率值明显增大,索越短,增长幅度越大,其影响不可忽略;随着减振架刚度减小,吊索反相整体振动模态的自振频率增长幅度略有减小。
(3)减振架位置对吊索反相振动模态的自振频率及振型有显著影响,随着减振架刚度减小,其影响逐渐减小。
(4)与刚性减振架相比,弹性减振架导致反相振动模态的自振频率值降低,减振架刚度越小,其差值越大;减振架的刚度及相对位置一定时,吊索自振频率与刚性减振架情况下的差值百分比受索长影响,索长越长差值百分比越小;随着减振架刚度增大,差值百分比随索长增长而减小的相对幅度增大;对于不同长度的吊索,当设置的减振架刚度k≥5×106N/m时,均可近似视为刚性减振架。
