亚纯函数微分多项式分担多项式的唯一性

张伟杰， 王新利

（上海理工大学 理学院，上海 200093）

1 主要定理

本文提到的亚纯函数即复平面上的亚纯函数，使用Nevanlinna值分布论中的基本记号[1-3]，如，，等。对于非常数的亚纯函数，一般用表示满足的量，其中，。

1996年，Fang等 研究了整函数分担一个非零常数的问题，得到了定理1。

1997年，在Fang等[4]研究的基础上，Yang等[5]进一步研究了非常数亚纯函数分担一个值的问题，提出了定理2。

定理2设和为非常数亚纯函数，且为正整数。如果和分担CM，其中 ，， 则，，，，为常数，且满足，或者，，其中，t 为常数，且。

2000年，Fang等[6]将分担一个“值”推广到分担“”，证明了定理3。

定理3设和为非常数亚纯函数，且为正整数，如果和分担CM，则，，其中，，，为有限非零复常数，且满足，或者，，其中，t 为常数，且。

2011年，Qiu[7]将分担“”推广到了分担一个多项式，得到了定理4。

定理4设和为超越亚纯函数，为正整数，且满足。是一次数为的多项式，如果和分担CM，则有，为常数。

本文将定理4的条件“CM分担”改为“IM分担”进行了研究，即下面的定理5。

定理5设和为超越亚纯函数，且为正整数，如果和分担∫PIM，P为非零多项式，且， 则，∫，其中，为常数，且满足，或者，，其中，t为常数，且。

2 引 理

引理1[1]设为非常数亚纯函数，为正整数，为的小函数，则

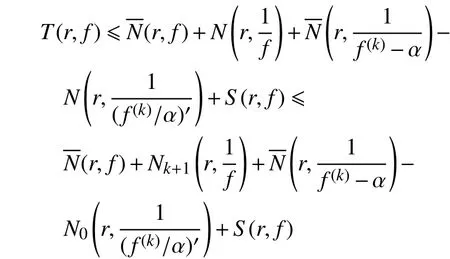
引 理2[3]设为非常数亚纯函数，为正整数，则

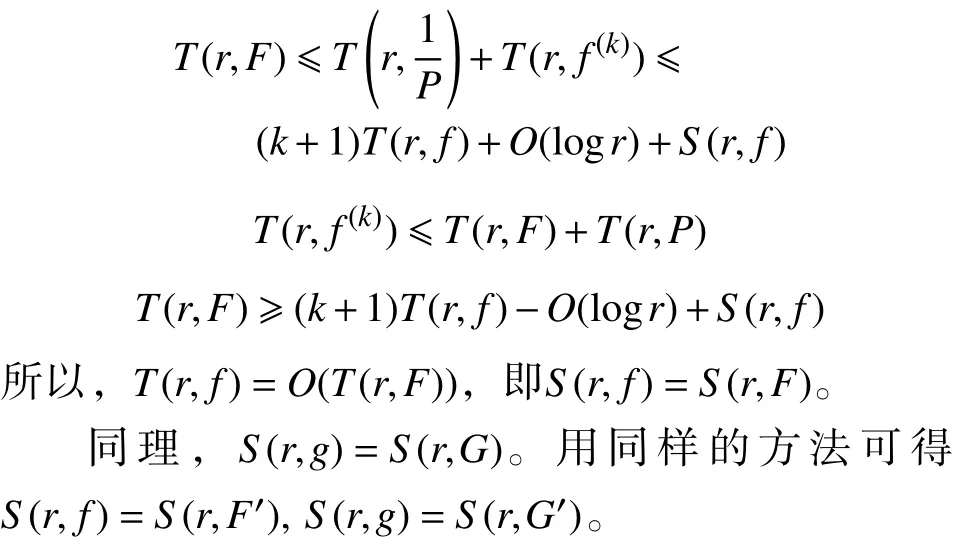
引 理6设和为非常数亚纯函数，为正整数，为一非零多项式。如果和分担IM，且满足

证明令

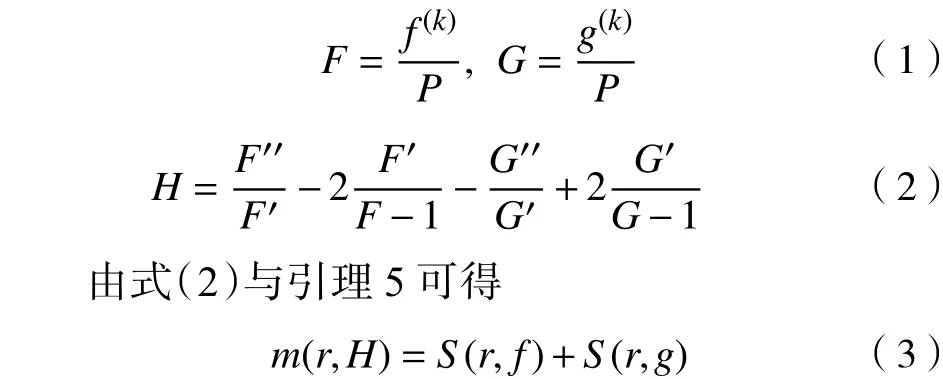
由式（2）可知，H的极点可能来自于F-1和G-1的零点重数不同的零点，F和G的极点，F′和G′的零点，且H的每个极点都为单极点，因此，

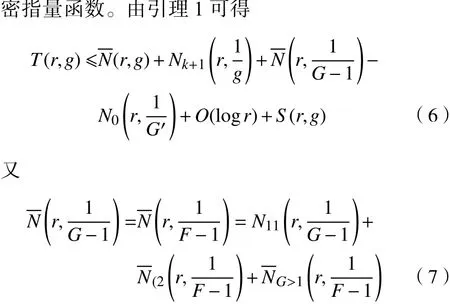
结合式（4）～（7），可得

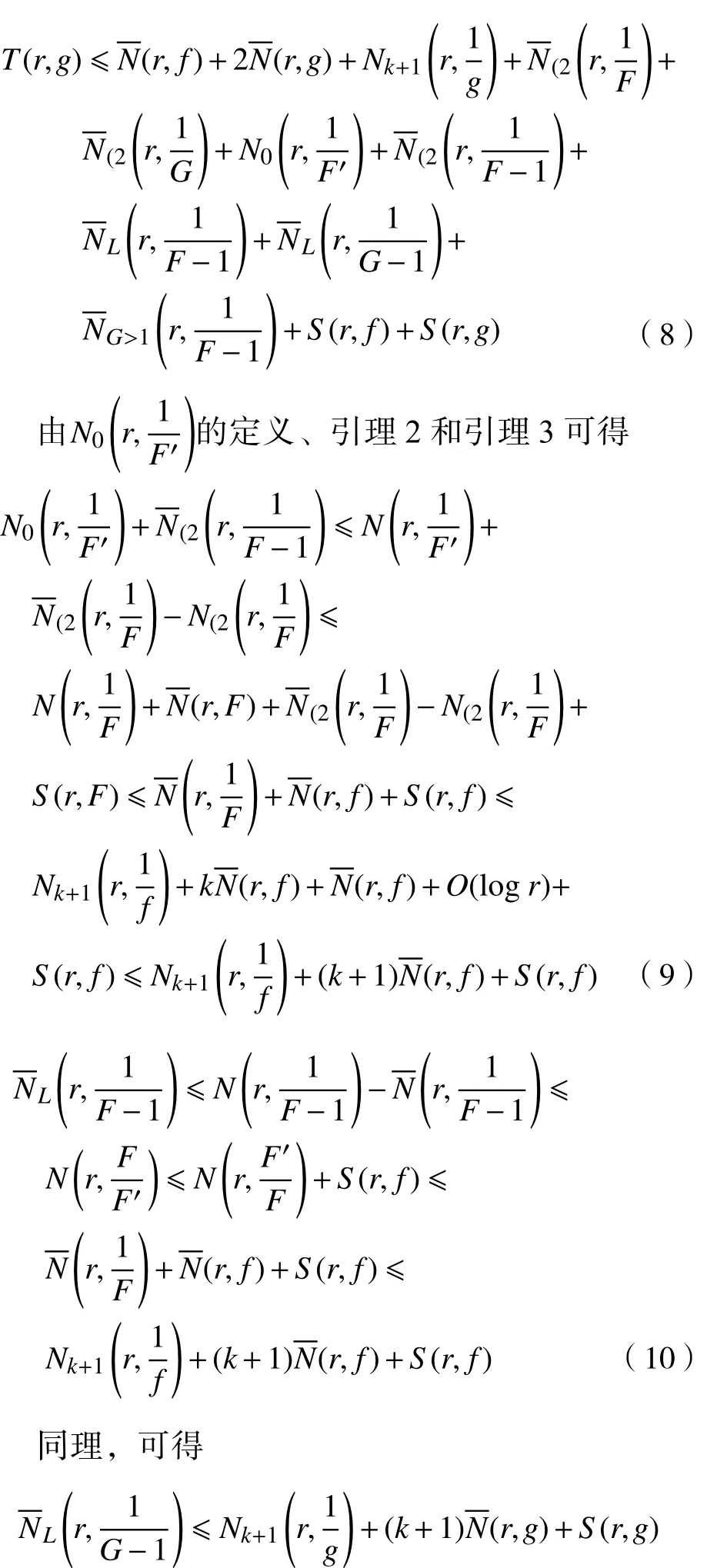
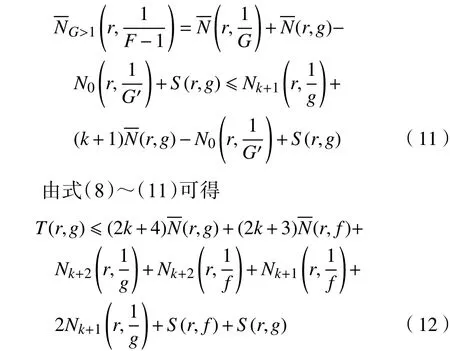
3 定理5的证明

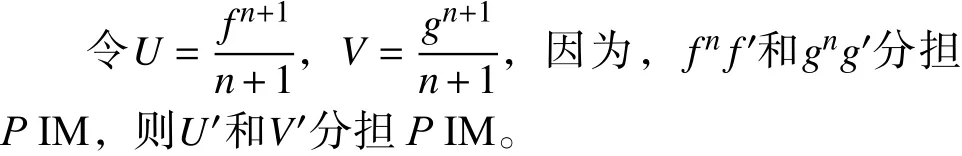
结合式（13）、式（15）和引理 2，可得

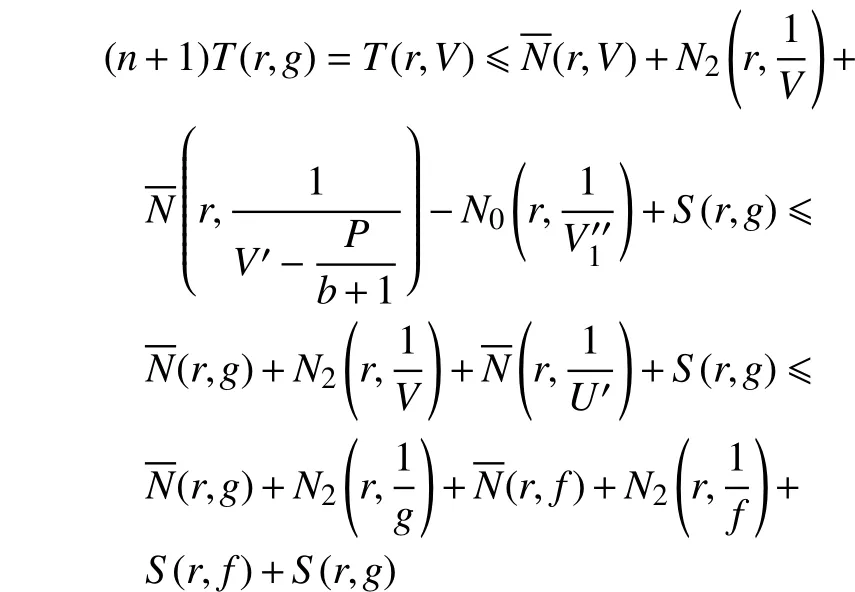
与情形1的b中的讨论类似，可得矛盾。因此，情形2不成立。

定理5证毕。