渠道土壤含水率的时空变化及渗漏模拟研究
2020-07-06魏占民张金丁杨旭东苏日娜
张 健,魏占民*,张金丁,杨旭东,苏日娜
(1.内蒙古农业大学 水利与土木建筑工程学院,呼和浩特 010018; 2.内蒙古自治区水利新闻宣传中心,呼和浩特 010000)
0 引 言
【研究意义】渠道渗漏是灌区灌溉水利用效率测算、灌区规划、设计运行管理、渠道防渗措施效果评价、区域水资源供需平衡计算的重要依据[1-2]。渠道渗漏问题的研究及其成果应用一直是水利工程领域重要的研究课题之一。【研究进展】国内外学者已针对渠道水分入渗致使土壤含水率发生变化方面展开了大量的研究,毛晓敏等[3]模拟结果表明,均质土的土壤含水率在椭圆区域边缘变化明显。而层状土的湿润峰向周边区域并非均匀规则推进,各层土壤含水率有明显差别。张金丁等[4]研究认为,在渠道水深作用下,渠床土壤含水率动态分布受基质势梯度、土壤导水率及湿周的影响较大。关于层状渠道的研究表明,土壤含水率分布具有不连续性,受夹层土壤质地影响显著,当湿润锋穿过夹砂层后,夹砂层内的土壤含水率明显小于其饱和含水率[5-8]。目前,渠道渗漏试验的数值模拟及入渗模型研究仍是热点。张茜媛[9]利用渠道渗漏有限元计算分析表明,地下水位埋深较浅时,渠道水位和地下水位深度对渠道渗漏量影响较大。李玥[10]基于HYDRUS 软件模拟不同边界条件下的试验,探寻5 个因素之间的交互作用,拟合出多影响因素下累积入渗量和湿润锋运移距离的计算模型。赵志强等[11]研究表明,HYDRUS-2D 软件建立水分二维运动模型能较好反演土壤水力特性参数,模型模拟值与实测值吻合。研究表明均质土壤和层状土壤的水分运动具有很大的差异,使得入渗过程变得较为复杂[12-14]。【切入点】以往虽然已进行了大量渠道渗漏的试验、理论分析及模拟研究,但研究大多是针对渠道渗漏量的室内模拟试验和计算,多围绕于一维土壤水分入渗问题,较少涉及水深对渠道土壤水分入渗的影响,渠道水分入渗致使土壤含水率时空分布变化的研究仍不多见。【拟解决的关键问题】因此,有必要开展实际情况下渠道渗漏的试验研究,探究渠道水深变化对土壤水分入渗及周边土壤含水率时空分布的影响,模拟分析不同质地的土壤水分入渗规律。本研究可为灌区节水工程改造实施、灌溉水有效利用系数的控制指标及区域水资源评价等提供技术支持。
1 试验与方法
1.1 测试方法
试验于2017 年5 月在内蒙古巴彦淖尔市临河区永济试验站进行,试验站位置坐标为E107°24′,N40°46′,试验期间观测地下水水位介于4.24~5.17 m之间。站内备有小型自动农田气象站,监测内容包括:环境温湿度、风速风向、累积降雨量、大气湿度等气象数据。该区为温带大陆性气候,年平均降水量142.1 mm。2017 年6 月开始在试验区域内取土样,土壤剖面深度为200 cm,采用型激光粒度分析仪对土样做土壤颗粒分析,利用饱和渗透仪,采用常水头法测定饱和导水率。试验区土壤颗粒分布及土壤干体积质量见表1,表2 为不同深度土层饱和土壤体积含水率。
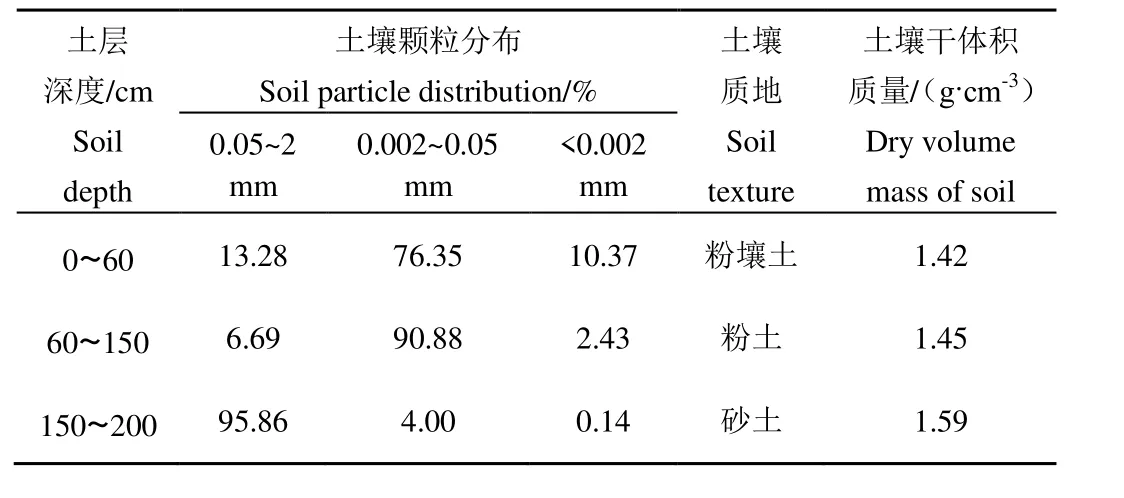
表1 试验区土壤质地 Table 1 Soil texture of test area

表2 不同深度土层饱和土壤体积含水率 Table 2 Saturated soil volumetric moisture content at different depths
1.2 试验设计
试验渠道长度为30 m,梯形断面渠道底宽1 m,断面水深1.2 m,设计最大水深1 m,边坡系数1.0,渠道顶宽3.4 m。依照《渠道防渗工程技术规范GB50600—2010》[15]需修筑隔离堤和渗漏平衡区,渠道渗漏试验采用恒水位静水位法。测试渠道的布设内容为:渠底布置3 根TDR 管,间距为50 cm;在渠道边坡上布置2 根TDR 管,水平间距为60 cm;在渠道坡顶处布置4 根TDR 管,间距为30 cm。测试渠道的观测内容:用水尺观测水位的变化;用秒表记录水位下降的时间;气象站可记录降雨时段及降雨量;在试验开始前和结束后用Diviner 2000 型便携式TDR 土壤水分廓线仪测定不同位置处不同深度的土壤含水率,并且在试验进行中每隔1 h 或2 h 测定1 次土壤含水率。
设渠道水深为试验变量,渠道水深变化范围为30~100 cm,间隔为10 cm,共8 个水深,采用统一的方法进行渠道入渗试验。试验开始时从临近水源(水井、机电井)用水泵同时向测验段、渗漏平衡区注水,并保持两侧水位基本相同,在试验进行的同时进行降雨量的观测。
1.3 HYDRUS 模型建立
1.3.1 渠道水分运动模型

渠道水分入渗过程属于二维入渗,采用修正的Richards 方程描述渠道水分运动模型方程: 式中:θ为土壤体积含水率(cm3/cm3);t为入渗时间(min);h为基质势(cm);x、z为水平坐标和垂直距离,规定z向下为正(cm);K(θ)为非饱和导水率(cm/min)。
土壤水力函数方程选用Van Genuchten-Mualem公式,表达式为:

式中:Ks为土壤饱和导水率(cm/d);θe为土壤相对饱和度;θr为土壤剩余体积含水率(cm3/cm3);θs为土壤饱和体积含水率(cm3/cm3);n是经验拟合参数,其中m=1-1/n,α是进气值倒数,与土壤物理性质有关的参数(cm-1);l为经验拟合参数,通常取其平均值为0.5[16]。
本试验仅涉及土壤水分运移模拟,故模型参数率定主要为土壤水力特性参数,即VG模型参数的率定。分析过程采用RETC 软件结合土壤水分特征曲线实测数据及实测的饱和含水率、饱和导水率计算得到每个土层的初始土壤水力特性参数。将上述土壤水力特性参数输入模型进行求解,结合HYDRUS-2D 模型反解模块利用实测的累积入渗量资料对土壤水力特性参数进行进一步的调整确定。即利用模拟值与实测值比较试算土壤水力特性参数的相对精确值,从而确定VG 模型参数,具体土壤水力特性参数初始值见表3。

表3 试验土壤VG-M 模型水力特性参数初始值 Table 3 Initial hydraulic characteristics of soil VG-M model
1.3.2 初始条件设置
因渠床土壤及渠道边坡下方湿润土体均为不规则的非饱和带,将模拟分析的过程概括化的整个模拟区域的初始含水率有规则的分散成若干含水率模拟区块,故初始条件可设置为:
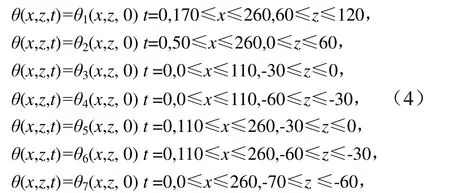
式中:θ1~θ7为不同模拟区块初始体积含水率,初始值:θ1=0.258 8,θ2=0.45,θ3=0.45,θ4=0.389,θ5=0.45,θ6=0.321 3,θ7=0.168 7,单位为cm3/cm3。
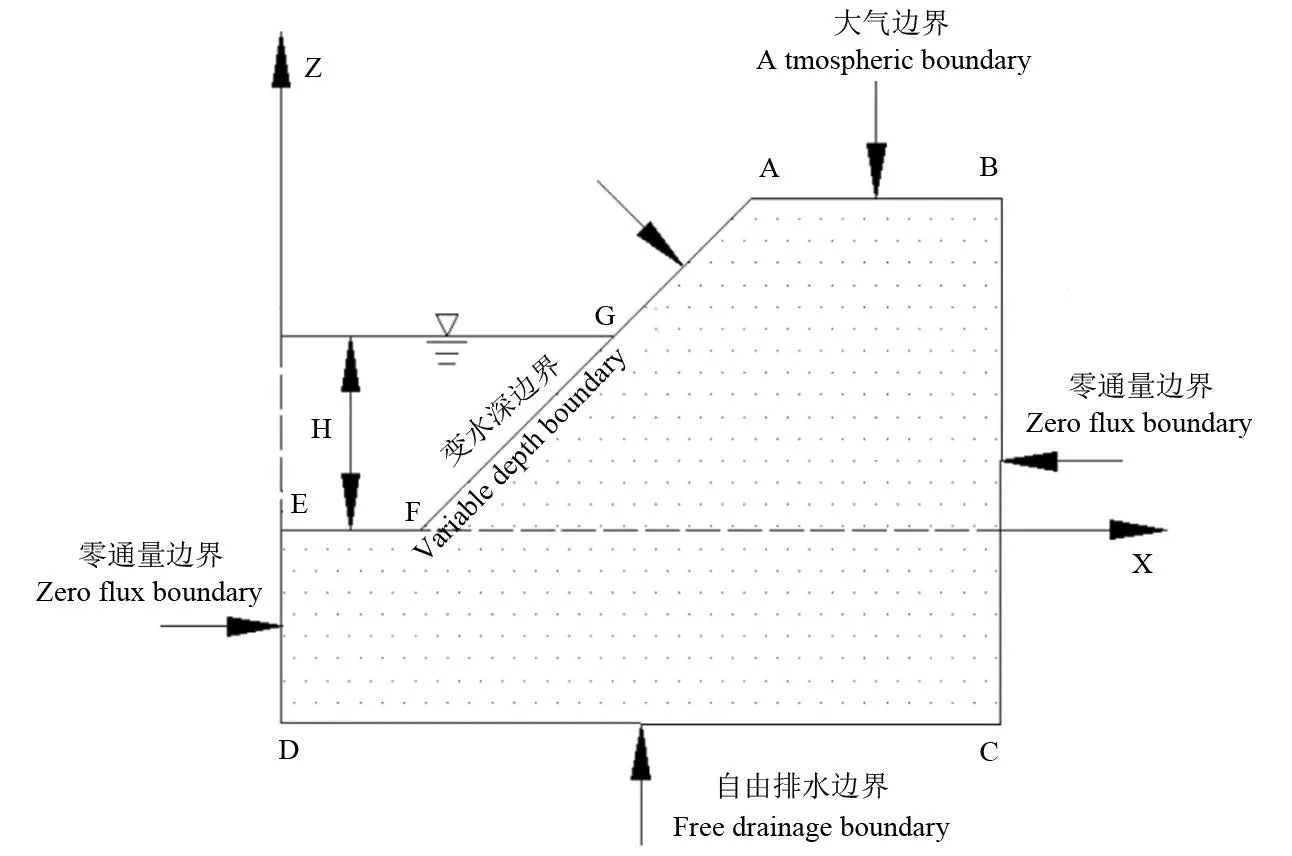
图1 模拟渠道边界条件 Fig.1 Schematic diagram of simulated channel boundary conditions
1.3.3 边界条件设置
图1 为模拟渠道边界条件。由图1 可知,渠道关于ED 所在面对称,故在模拟渠道入渗过程中只需考虑ABCDEFG 区域内的土壤水分运动即可。因试验的特殊性,在水位下降静水测渗试验的准备阶段需将渠道里的水量加到特定渠道水深,在加水的过程中渠床表层土壤便已被水分湿润至接近饱和状态,水深最深的情况下土壤含水率基本处于饱和状态。故EF 和FG边的初始条件可设为饱和含水率,在不同渠道水深情况下,这一饱和体积含水率的值均为0.45 cm3/cm3。渠道水深以上部分,GA 和AB 边界接触大气,选择大气边界。因模拟区域关于ED 所在面对称,故左边界ED 可视作水平通量为0,设为零通量界面;右边界BC 亦视为零通量界面;下边界DC 视为自由排水边界。
2 结果与分析
2.1 渠道土壤含水率的时空变化研究
为探究渠道入渗过程中土壤含水率的时空变化规律,本研究位置选取在距离渠道中心线右侧50 cm 处。由图2 可知,不同时刻土壤含水率在剖面分布变化较为明显,试验开始运行0 h 时,竖直方向100~140 cm土壤含水率值相近,在38.30%~41.58%之间变化;随着剖面深度的增加,150~170 cm 土壤含水率值对应的数值越小,由28.68%减小到14.19%。试验进行2 h 后,100~120 cm 土壤含水率值基本达到饱和,随着时间的延长,数值基本不变。土层深度为110 cm 和120 cm的含水率值相比初始时刻分别增加了9.45%和14.45%;而在120~130 cm 土层深度处,试验进行4 h 范围内,土壤含水率分布变化比较明显,含水率值依次增加2.73%、8.97%、11.47%。与上层土壤相比,入渗速率相对变慢,土壤达到饱和含水率的时间延长。由此可见,当土壤剖面存在分层界面时,临界面对水分的入渗具有缓阻作用,土壤达到饱和含水率的时间相应增长。在试验4~7 h 内,随着时间的推移,基本可达到均匀入渗。试验运行7 h 后,土壤剖面100~170 cm含水率趋于稳定,随着时间的推移,含水率数值无明显变化,土体含水率近乎为饱和含水率。

图2 不同时刻土壤含水率剖面分布 Fig.2 Sections of soil moisture content at different times
由图3 可知,100~120 cm 土层土壤含水率的变化规律基本一致,2 h 范围内呈线性增大,而后含水率值再无明显变化,土壤达到饱和含水率的时间相对较短。土层深度为110 cm 处,初始含水率值为41.58%,2 h 内含水率值相对增加9.45%,而后基本趋于稳定;120 cm 土层深度处,初始含水率值为41.58%,2 h 含水率值相对增加14.45%,而后趋于饱和含水率。130 cm 土层深度处,在5 h 范围内,随着时间的推移,含水率值相应增加2.73%、8.97%、11.47%、17.77%,而后土壤含水率趋于稳定,可见土壤含水率变化明显且达到饱和的时间相对较长,这是因为土壤剖面土质的层状性,致使在5 h 范围内土壤含水率的变化较为显著,达到饱和含水率的时间较长。土层深度为150~170 cm 处,含水率的变化规律为前期含水率值基本为土壤初始含水率值,而随着水分入渗穿过土质分界面后,土壤含水率值基本呈线性增加,而后趋于稳定,达到土壤饱和含水率。由此可见,当土壤剖面存在分层界面时,临界面对水分的入渗具有缓阻作用,土壤达到饱和含水率的时间相应增长,且到达一定时间后,缓阻现象消失,水分通过分层界面后,呈线性均匀的变化,这是因为分层界面上下的基质势不同,当湿润锋运移至分界面时,湿润锋的基质吸力大于下层土壤的进水吸力,随着时间的延长上层土壤趋于饱和,上层基质吸力小于下层土壤的进水吸力时,水分穿过分层界面入渗到下层。这与李卓、范严伟[12,14-17]的结论一致。

图3 不同土层深度土壤含水率随时间变化 Fig.3 Soil moisture content changes with time at different depths of soil layers
2.2 不同水深条件下渠道渗漏及模拟分析
2.2.1 入渗速率的变化及模拟分析
选取渠道水深H为40、60、80、100 cm 的试验进行研究。由图4 可知,4 种渠道水深相应的稳定入渗速率依次为1.070、1.467、1.610、2.155 cm/h;到达稳定入渗的时间为4.48、3.99、3.50、2.79 h。相对于H为40、60、80、100 cm 水深条件下稳定入渗速率相应增加33.85%、46.90%、101.10%,达到稳定入渗的时间依次减小0.71、1.20、1.69 h。由此可见,试验均呈现出初期入渗速率变化由快逐渐变慢,到达一定时间后基本趋于稳定。随着渠道水深的增大,对应的稳定入渗速率越大,到达稳定入渗的时间越短。这是因为水分在土壤内运动,势能的变化为主要驱动力,渠道水深的变化导致压力势变化,即入渗水头对渠道水分入渗影响显著,研究成果与李红星[18]的一致。基于HYDRUS-2D 模拟实际土壤条件下的渠道渗漏,模拟值和实测值的变化趋势基本吻合,4 种水深实测值和模拟值的RMSE的值为0.002 9、0.005 1、0.004 9、0.015 2 cm/h,R2的值为0.99、0.96、0.97 及0.95,说明模拟效果较好。

图4 不同水深条件下入渗率的实测值和模拟值 Fig.4 Measured and simulated values of infiltration rates under different water depths

图5 不同水深条件下累积入渗量的实测值和模拟值 Fig.5 Measured and simulated values of cumulative infiltration under different water depths
2.2.2 累计入渗量的变化及模拟分析
图5 为不同水深条件下累积入渗量的实测值和模拟值对比。入渗时间为23.85 h 时,4 种水深相应的累积入渗量依次为0.55、1.25、2.11、3.99 m3。相对于水深H为40、60、80、100 cm 累积入渗量相应增加89%、219%、1 319%。由此可见,试验累积入渗量的变化基本均呈线性变化规律,且随着渠道水深的增大,累积入渗量的变化越大。这是因为势能的变化为水分在土壤内运动的主要驱动力,渠道水深与土壤水势梯度正相关,因而与渗漏通量正相关,渠道水深的变化导致渗透通量变化,得出入渗水头(渠道水深)为影响渠道渗漏的主要因素,研究成果与李红星、张建丰[18-19]的结论一致。
模拟值和实测值的变化趋势基本吻合,4 种水深试验实测值和模拟值的RMSE的值为0.001 9、0.002 5、0.003 9 和0.091 7 cm/h,R2的值为0.99、0.98、0.96及0.93,说明试验模拟效果较好。结合对渠道入渗速率及累积入渗量的模拟结果,可知所选定的土壤水分运动方程合理,参数值合适,用于渠道渗漏评价入渗速率和累积入渗量可行。
2.3 基于HYDRUS 模拟不同土质渠道渗漏

图6 不同土质条件下入渗速率 Fig. 6 Infiltration rates under different soil conditions
选取试验渠道内粉土及粉壤土进行均质渠道渗漏模拟研究,土壤含水率见表2;模拟试验采用HYDRUS-2D 软件,具体土壤水力特性参数值见表3。如图6、图7 所示,3 种类型土壤的入渗速率变化均呈现入渗初期速率较大,在一定时间内逐渐减小,而后趋于稳定;累积入渗量的变化基本呈线性增加的变化。0.9 h 内粉壤土及层状土的入渗速率基本一致,粉壤土在0.9~5.62 h 时间范围内呈线性减小,而后趋于稳定;层状土在0.9~1.56 h 呈非线性减小的变化,1.56 h 后趋于稳定。表明2 种土质条件下入渗速率在湿润锋到达砂层前与粉壤土基本一致,但由于层状土内砂土具有一定的阻水减渗性[5-7],使得水分进入砂层前呈非线性缓慢地变化,进入砂层以后,入渗率为常数,即转为稳定入渗过程,这与张建丰[19]的研究结论一致。粉壤土的稳定入渗速率相比粉土增大30%,而28.97 h 时的累积入渗量增大56.3%,这是因为粉土中含有粉粒,砂粒量相对较少,故相对于粉壤土,粉土的进水吸力明显大于砂壤土,其持水能力相对较大,入渗速率较小,累积入渗量较小。因此,渠道土质越黏重,土粒间孔隙就越小,水流渗漏的阻力越大、水力传导度越小,土壤持水能力越大,渠道的渗漏损失越小结论与高峰[20]的结论一致。

图7 不同土质条件下累积入渗量 Fig.7 Cumulative infiltration amount under different soil conditions
3 讨 论
本研究在渠道有压入渗条件下采用恒水位静水试验的方法进行渠道渗漏研究,分析渠道土壤含水率的时空变化规律,探究不同水深条件下渠道的累积入渗量及入渗速率的变化规律。基于田间层状土壤条件下开展的渠道渗漏试验研究,建立了二维空间上饱和-非饱和有压水头的土壤水分入渗模型,采用HYDRUS-2D 软件对试验渠道及均质粉土、粉壤土的渠道进行模拟。但只针对渠道内的2 种土壤进行模拟研究,此外应开展多种质地条件下均质及层状组合的渠道水分渗漏分析,且影响渠道渗漏的因素较多,未来有必要进行众多试验探索渠道渗漏的主要因素,并开发多因素交互情况下渠道渗漏损失计算公式。
4 结 论
1)当土壤剖面存在分层界面时,时间在2~5 h内,临界面处含水率值依次增加2.73%、8.97%、11.47%、17.77%,随着时间的延长,土壤含水率逐渐趋于稳定,可见临界面对水分的入渗具有缓阻作用,土壤达到饱和含水率的时间相应增长,且到达一定时间后,缓阻现象消失,水分通过分层界面后,呈线性均匀的变化。
2)利用HYDRUS-2D 软件对试验渠道的水分入渗速率及累积入渗量进行模拟效果较好,用于渠道渗漏评价入渗速率和累积入渗量是可行的。分析得出随着渠道水深的增大,入渗速率越大,累积入渗量的变化越大。
3)粉壤土的稳定入渗速率相比粉土增大30%,而时间为28.97 h 时累积入渗量增大56.3%。
