可燃物含水率实时变化的预测模型1)
2010-08-08曲智林李昱烨闵盈盈
曲智林 李昱烨 闵盈盈
(东北林业大学,哈尔滨,150040)
森林可燃物的含水率是决定林火发生以及林火蔓延的重要指标,因此森林可燃物含水率变化规律的研究对于预测林火发生和控制林火蔓延都具有重要的意义。而研究森林可燃物含水率变化规律一般通过建立其数学模型来实现,如Viney[1]、金森[2]等给出了在温度恒定条件下,较小的可燃物含水率变化模型,Catchpole[3]等提出了一种可燃物含水率的预测方法。也有通过建立平衡含水率模型来预测可燃物的含水率,如金森等[4]给出了自然环境中可燃物含水率的理论预测方法,目前可燃物平衡含水率模型主要有 Simard模型[5]、Van Wagner 模型[5]、Anderson 模型[6]、Nelson 模型[7]等。这些模型都有各自的特点,也存在一定的局限性,为实际中的使用带来一定的困难。笔者根据试验地的观测数据,建立了一个平衡含水率随影响因子动态变化的可燃物含水率实时变化预测模型,拟通过此模型可以根据某一时刻各影响因子的值预测下一个时刻可燃物的含水率,这样可以为较准确地预报林火发生以及控制林火蔓延提供理论根据。
1 研究方法
1.1 数据的获取
所用数据为2009年3月18日—2009年4月30日黑龙江省海林县石河子林场试验地的观测数据,观测木为长20 cm,外直径为2.6 cm,内直径为2.1 cm的内空的椴木。观测木安装在观测仪器上,观测仪器每小时自动收录各项数据。收录的数据包括时间、气温、相对湿度、风速、风向、降雨量、观测木的含水率和温度等。
1.2 模型建立
由于可燃物的含水率变化受降雨量多少的影响较大,且它们之间的关系较为复杂,因此本研究的模型建立在多时无降雨的情况下,在固定区域和特定时段内可燃物含水率预测模型的影响因子为当时空气温度、空气中相对湿度、风速和可燃物的含水率。
文献[7]中的研究表明:可燃物含水率的瞬时变化率主要受可燃物的含水率与其平衡含水率的影响。因此可燃物含水率变化模型为:

其中:Mt为可燃物t时刻的含水率(%);Et为可燃物t时刻的平衡含水率(%)。
而可燃物t时刻的平衡含水率由当时大气中的相对湿度、风速和温度决定[7]。根据对各影响因子的分析,选取

式中:Ht为大气中t时刻的相对湿度(%);Wt为风速(级);Tt为t时刻温度(℃)。
则得到可燃物含水率实时变化预测模型(1 h内变化)

利用此模型可由t时刻的可燃物含水率、气温、相对湿度和风速得到t+1时刻可燃物的含水率。利用SPSS12.0和STATISTICA6.0软件完成数据处理。
2 结果与分析
2.1 可燃物单位时间内含水率改变量与各影响因子的关系
利用试验地2009年3月18日至4月30日的观测数据(剔除受降雨影响的数据,并温度在零度以上,共595个样本)分析了可燃物1 h内含水率改变量与当时空气温度、空气中相对湿度、风速等各影响因子的关系。从图1可以看出可燃物1 h内含水率改变量多少受前一时刻的相对湿度的影响,随着相对湿度的增加,可燃物1 h内含水率改变量也相应增加。
从图2可以看出可燃物1 h内含水率改变量多少受前一时刻的气温高低的影响,随着气温增高可燃物1 h内含水率改变量也相应减少。
从图3可以看出可燃物1 h内含水率改变量多少受前一时刻的气温高低的影响,随着气温增高可燃物1 h内含水率改变量也相应减少。这里给出的线性方程,只是说明两者之间的变化关系,并不表示线性关系最佳。图1—图3中的相关系数较低是由于单位时间内可燃物含水率变化量相对较小引起的,并不说明可燃物含水率改变量与空气温度、空气中相对湿度、风速等各影响因子的相关性小。
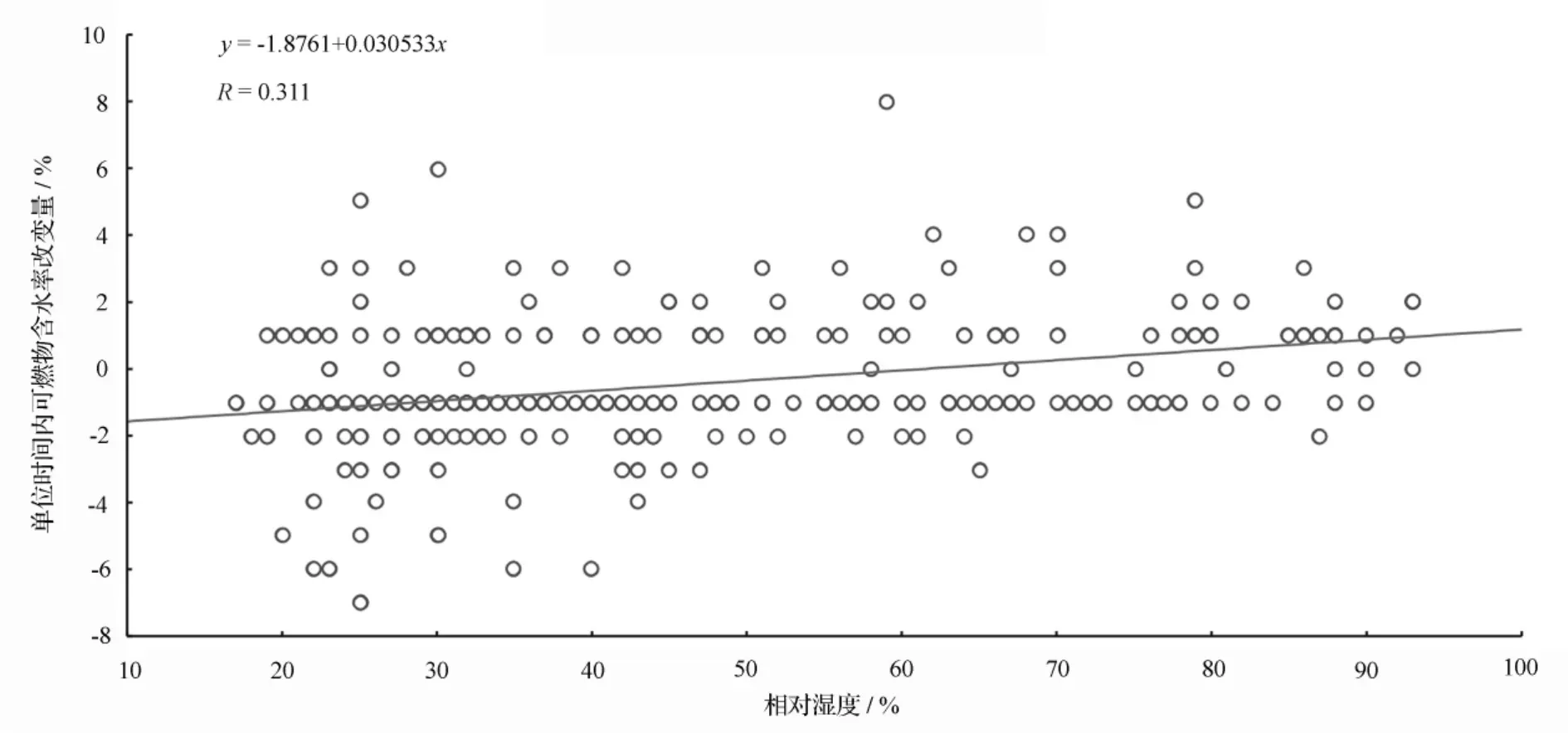
图1 单位时间内可燃物含水率改变量与当时相对湿度的关系

图2 单位时间内可燃物含水率改变量与当时气温的关系
2.2 可燃物含水率实时变化预测模型的构建
根据试验地的观测数据,统计出各影响因子的取值范围(见表1)。这里风速(v)分为6级,0级:0 表1 各影响因子取值范围 从试验地观测数据中随机选取480个用于建立模型,剩余115个用于对模型的检验。根据统计回归理论,对模型(3)的参数进行估算(见表2)。以上模型均通过t检验(α=0.05)。 表2 模型中的参数估计值 根据115个检验数据对模型进行检验,正确率98.0%(相对误差不超过5%),并给出了试验地2009年4月10日可燃物含水率的实时实测值与预测值(见表3),两者之间较为一致,说明该模型基本反映了可燃物含水率实时变化规律。 图3 单位时间内可燃物含水率改变量与当时风速的关系 表3 2009年4月10日试验地可燃物含水率的实测值与预测值 给出了可燃物含水率实时变化预测模型,该模型在多时无雨且温度在零度以上的条件下根据某时的相对湿度、气温、风速以及可燃物含水率值能够预测1 h后可燃物的含水率,经检验模型精度达98.0%(相对误差不超过5%),基本上反映出相对湿度、气温、风速与可燃物含水率变化率的关系。因此该模型在温带针阔混交林区,3—4月份及多时无雨且温度在零度以上的情况下适用,可用来预测可燃物含水率。 选用的观测木是枯死的椴木段,因此所建模型只适用于枯死椴木,对于其它树种,可以根据相类似的方法构建模型。 对于在有降雨的情况下,可燃物含水率的变化规律较为复杂,没有讨论;另外模型中的风速的单位是级,如换成m/s,模型的精度会有所提高,今后将对模型做进一步的改进。 [1] Viney N R,Catchpole E A.Estimating fuel moisture response time from field observations[J].International of Wildland Fire,1991,1(4):211-214. [2] 金森,李绪尧,李有祥.几种细小可燃物失水过程中含水率的变化规律[J].东北林业大学学报,2000,28(1):35-38. [3] Catchpole E A,Catchpole W R,Viney N R.Estimating fuel response time and predicting fuel moisture content from field data[J].International Journal of Wildland Fire,2001,10:215-222. [4] 金森,姜文娟,孙玉英.用时滞和平衡含水率准确预测可燃物含水率的理论算法[J].森林防火,1999(4):12-14. [5] 刘曦,金森.平衡含水率法预测可燃物含水率的研究进展[J].林业科学,2007,43(12):126-133. [6] Anderson H E.Moisture diffusivity and response time in fine forest fuels[J].Canadian Journal of Forest Research,1990,20:315 -325. [7] Nelson R M.Prediction of diurnal change in 102hour fuel moisture content[J].Canadian Journal of Forest Research,2000,30:1071-1087.

2.3 模型的检验


3 结束语
