基于矩阵分解的超奈奎斯特接收技术
2020-07-04苏凤轩
苏凤轩
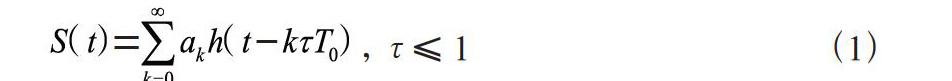


摘 要:通信传输系统中引入超奈奎斯特信号进行传输时,对码间干扰等问题进行了研究。为了降低码间干扰,提出了利用基于矩阵分解的方案消除超奈奎斯特码间干扰用以提高系统传输的性能。该方案运行时独立于网格状态,首先在发射端处采用相应预编码进行降低干扰,其次在接收端处利用分解进一步消除干扰,消除干扰后的信号通过相关信道译码,最后利用硬判决恢复出原始信息。仿真验证结果表明,基于矩阵分解的FTN传输系统可以进一步提高系统的性能。
关键词:超奈奎斯特;码间干扰;矩阵分解;预编码
中图分类号:TN911.4 文献标识码:A 文章编号:2096-4706(2020)03-0047-03
Abstract:When the Faster-Than-Nyquist signal is introduced in a communication transmission system for transmission,the existence of inter-symbol interference and other issues are studied. In order to reduce the existing inter-symbol interference,a solution based on matrix factorization is proposed to eliminate the inter-symbol interference of Faster-Than-Nyquist to improve the performance of the system transmission. The scheme is independent of the ISI grid state. First,the corresponding precoding is used at the transmitter to reduce interference,and then is to use the decomposing at the receiver to further eliminate interference,and the signal after interference is decoded through the relevant channel. Finally,the original information is recovered by using the hard decision. Simulation results show that the Faster-Than-Nyquist transmission system based on matrix decomposition can further improve the system performance.
Keywords:FTN;ISI;matrix decomposition;precoding
0 引 言
作为5G的候选技术,FTN信号因其高频谱效率而受到越来越多的关注[1]。1970年,Mazo提出超奈奎斯特(Faster- Than-Nyquist,FTN)的概念,表明了传输速率比奈奎斯特所定义的更快,同时系统的误码性能也不会降低。奈奎斯特强调信号的正交性以避免符号间干扰,FTN引入的码间干扰(Inter-Symbol Interference,ISI)進行非正交传输,导致牺牲带宽效率来维持正交性。
为了解决这个问题,已经提出了很多关于FTN信号接收端的检测方案,其中最为经典的算法就是最大似然序列估计[2](Maximum Likelihood Sequence Estimation,MLSE),但其复杂度极高。已知提出的M-BCJR算法是通过选择网格解码来降低接收端检测的复杂度,其复杂度依旧很高。因此,针对超奈奎斯特干扰消除问题提出了一种基于矩阵的相关算法,分别提出了基于QR分解和基于矩阵上下三角分解的算法。基于矩阵的算法是利用矩阵相关计算来消除码间干扰。最后的仿真结果也表明了基于矩阵算法的检测方案性能优于基于网格解码的方案。但是上述所提出的矩阵相关算法忽略了数据帧之间的干扰,因此其性能还有待提高。
针对以上问题,本文提出了一种新的关于超奈奎斯特码间干扰消除的方案:首先发射端采用预编码以及信道编码后的符号经过调制后插入循环前缀,其次根据预编码矩阵与干扰矩阵H之间的关系对发送端的信号降低干扰;接收端进行相关分解,使得ISI被完全消除。同时,本文提出的方案是独立于ISI网格解码[3],无需考虑网格解码的计算。最后将本文提出的方案分别与其他方案进行仿真分析比较。
1 系统模型
1.1 FTN系统模型
对于基带信号的线性调制h(t)的FTN传输系统,其发送端信号可表示为:
式中,S(t)表示接收信号,ɑk表示符号信息。对于FTN信号,每个符号的时间间隔Ts=τT0(0<τ<1),τ表示符号压缩因子。
与正交传输不同之处在于FTN传输系统存在一个符号压缩因子τ,使得发送信号的速率变得更快。当τ<1时,ISI随着τ值变化,传输速率越大,τ值越小,导致引入的ISI也越严重。当τ=1时,传输的正交信号在接收端不受ISI的影响。
根据以上所述,本文提出基于矩阵分解消除ISI的FTN系统框图,如图1所示。信号首先进行信道编码,编码后的信号再进行调制,之后插入的循环前缀(Cyclic Prefix,CP)合成帧结构。此结构可以有效阻隔数据帧之间受到的干扰。然后再经过预编码用以降低发送端信号的ISI,最后经过FTN成型滤波器后得到符号间隔为τT0的FTN传输信号,实现发送端的FTN传输。
接收端接收到的信号首先经过FTN匹配滤波器,随后对信号以τT0的符号间隔进行下采样,经过分解后消除ISI的同时去除循环前缀再进行译码,最后恢复出原始信息。
FTN传输模型中,接收端接收到的信号序列表示为:
rm和 分别表示接收端的第m个采样信号以及高斯白噪声w(t)经过匹配滤波器之后所引入的噪声序列。在FTN信号中,检测第k个符号ak时会受到前一个符号ɑk-1和后一个符号ɑk-1的干扰,且干扰符号的数量是由τ值而决定。因此可以得到h-1和h1是第一干扰系数,其值相等,以相同的方式得到,h-2和h2是第二干扰系数,其值相同,以此类推得到其他的干扰系数。
接收信号R由滤波器系数和传输的数据符号卷积所表示。对于一般的结构,接收信号经过匹配滤波器和采样后输出以矩阵形式表示为:
1.2 基于矩阵特征分解的预编码和分解
由上述分析可以得到,在高斯信道中进行FTN传输时,受到的符号间干扰由FTN产生的,且干扰用矩阵H表示。另外,添加的循环前缀阻隔了数据帧之间的相互干扰。因此本文提出了一种简单且性能较好的符号间干扰消除方案。
在发射端,信号序列通过预编码矩阵UH得到:
2 性能分析和仿真结果
本文将提出的方案与其他方案分别在高斯信道中进行仿真分析比较。选取滚降衰落因子系数为β=0.3的根升余弦成型脉冲。
本文提出的算法相比其他算法,在发送端添加了循环前缀以阻隔数据帧之间的干扰,其长度S大于因FTN引入ISI长度和的一半。仿真过程中以QPSK(τ=1)调制的性能为参考,选取符号采样率是1 Hz,设置帧的长度L为1 024,滤波器的边带长度为10。在仿真过程中利用高斯信道,描绘了当时间压缩因子τ分别取0.90和0.82时,同等条件下的仿真图。
图2和图3显示了在高斯信道中当(τ=0.90)和(τ=0.82)时,基于QR分解和M-BCJR方案的误码性能与本文提出方案的FTN傳输误码率图。当(τ=0.90),RSN大于8时,基于QR分解方案的性能优于M-BCJR的算法。在τ=0.90,RSN=10时基于QR分解方案比M-BCJR的方案有大约0.3 dB的增益,此时,本文提出的方案性能比基于QR分解的方案大约有0.5 dB的增益,与M-BCJR的方案相比大约有0.7 dB的增益。当τ=0.90时,本文提出的方案误码性能曲线与τ=1.00时相接近,且误码性能可以达到10-5至10-6之间,
由两图对比可知,一方面,随着τ值的减小,FTN引入的ISI也会越严重,其系统误码性能也会随之变差,但是本文提出的方案系统性能始终优于其他方案;另一方面,系统为了有更好的误码性能,其τ值不宜过大或过小。
3 结 论
FTN信号提高了传输速率,但是也引入了不可避免的ISI,因此本文提出了一种基于矩阵的特征分解得到预编码和分解矩阵,避免了需要考虑ISI的网格状态与ISI抽头组之间的大小关系。最后通过仿真分析对比,得出本文提出的方案对系统的误码性能有着很大的改善。
参考文献:
[1] BANELLI P. Modulation Formats and Waveforms for 5G Networks:Who Will Be the Heir of OFDM?:An overview of alternative modulation schemes for improved spectral efficiency [J].Signal Processing Magazine,IEEE,2014,31(6):80-93.
[2] FORNEY,G,JR. Maximum-likelihood Sequence Estimation of Digital Sequences in the Presence of Intersymbol Interference [J].IEEE Transactions on information Theory,1972,18(3):363-378.
[3] BEDEER. E,AHMED M.H,YANIKOMEROGLU H.A Very Low Complexity Successive Symbol-by-symbol Sequence Estimator for Faster-than-Nyquist Signaling [J].IEEE Access,2017(5):7414-7422.
