整体关联，促进学生建构知识

翟莹

[摘 要]数学教学中，教师可从知识的整体关联入手，引导学生不断深入探究，使学生所学的数学知识形成一個有机的整体，实现从整体上提升学生数学核心素养的目的。

[关键词]整体;关联;建构;数学教学

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）21-0035-02

布鲁纳指出：“学习就是认知结构的组织与重新组织。”数学知识不是孤立存在的，而是相互关联的。但是，在平时的数学教学中，教师常常注重各个知识点的教学，忽视了数学知识之间的整体关联，不利于学生建构完整的知识体系。因此，教师应从学生已有的知识经验出发，将教学内容置于整个数学知识体系中去设计教学，引导学生经历知识发生、发展和形成的过程，使学生真正理解和掌握所学的数学知识，提升学生的数学学习效率。

一、注重数与数的关联，整体内化

数是数学的重要内容。在数的认识教学中，教师要善于从知识的本质入手，找准数的概念之间的联系，沟通数与数之间联系的纽带，然后连点成线，促进学生整体建构数的认知，真正内化所学的数学知识。

例如，以小数与整数教学为例，它们的本质都是十进制数，它们的计数单位之间存在着密切的联系，即可以把它们看作由计数单位1向两边无限延伸演变而成。因此，教师可从小数的意义入手，帮助学生建立起小数与整数之间的关联，使学生对数形成整体认识。课堂上，教师从认识1元、10元、100元的人民币入手，引导学生按照1、10、100之间的进率进行换算，并以100格的正方形纸为例，让学生说说分别是多少元。然后教师提出问题：“不满1格怎么办？”经过分析思考，学生得出结论：可以借助元、角、分的十进制关系，把整数之间相邻两个单位之间的进率定为十，这样把1平均分成10份，每份就是0.1元;不足0.1元时，再把0.1元平均分成10份，那么每份就是0.01元。这样将小数与整数结合起来进行教学，使学生体验到整数是学习小数的基础，实现数学知识的“再创造”。

数学教学中，教师要从整体上审视各个知识点，把握各个知识点的来龙去脉，帮助学生形成对所学知识的整体认知。数的范围很广，不仅包括整数和分数，还包括百分数等。因此，在数的认识教学中，教师要注重数与数之间的关联性，使学生明白各种数之间的联系，从而结点成网，形成关于数的认识的结构网络。

二、注重数与例的关联，整体贯通

“数学源于生活，用于生活，高于生活。”因此，教师要善于把教学内容置于学生熟悉的实际生活中，使其成为学生学习数学的内驱力。数学课堂中，教师可引导学生从整体上沟通知识之间的内在联系，实现学生数学认知的整体建构。

例如，教学《速度、时间和路程》时，学生通过字面意思对时间与路程有一定的了解，而对于速度，多数学生的认知停留在快慢的层面上。那么，怎样才能促进学生对问题的整体认知呢？首先，教师为学生创设具体的教学情境，引导学生比快慢：“假如小芳家到学校是240米，她用了5分钟走到学校;小明家到学校是250米，他用了5分钟走到学校。你知道他俩谁走得快吗？”这里，由于路程不同，“谁走得快”就是衡量速度的一个标准，教师这样教学水到渠成。其次，教师设计习题，让学生进行求速度的训练。在此基础上，教师引导学生总结出路程、速度、时间之间的数量关系。这样教学，使学生对路程、速度、时间之间数量关系的认识更加系统化，丰富了学生的数学认知。

数学教学中，教师通过创设问题情境，引导学生经历“引出模型——抽象模型——丰富模型”的思维过程，帮助学生获得对数学知识的本质认识，使学生形成对所学知识的整体建构。同时，这样教学有助于学生触类旁通、举一反三，积累更多的数学活动经验。

三、注重数与形的关联，整体重构

著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微;数形结合百般好，隔离分家万事休。”因此，数学教学中，教师要注重数与形之间的关联，从数学知识整体的角度，深化学生对所学数学知识的理解，实现优化数学教学的目的。

例如，计算破碎钟面的周长，有的学生说“这道题没法计算，要把钟面还原后才能求出它的周长”;有的学生说“要知道这个钟面的半径，才能计算出它的周长”。学生的思维陷于困境，于是教师提问：“怎样才能求出这个钟面的周长呢？能不能用类推的方法来解决呢？”在教师的启发下，学生想到可以先量出钟面的一大格，再把它乘以12（钟面有12个大格，每个大格的长度都相等）就可以得出钟面的周长了。这样看形思数、以数助形，帮助学生沟通了钟面大格、份数之间的关联，使学生形成钟面知识的整体建构。

数学教学中，教师应帮助学生形成对所学知识的整体认知，启发学生变换角度思考问题，这样有助于学生突破思维定式，将习得的数学知识融会贯通、重新建构，提高数学课堂教学效率。

四、注重数与法的关联，整体建构

数学思想方法是对数学知识、方法、规律的本质认识，是数学思维的结晶和概括，是解决数学问题的灵魂和根本策略。因此，数学教学中，教师要注重数学思想方法的渗透，使学生真正理解和掌握所学的数学知识，提升数学学习能力。

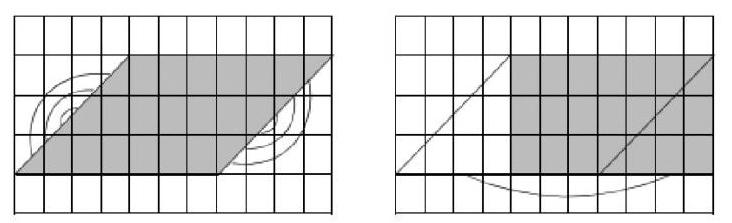
例如，教学《平行四边形的面积》一课时，这部分内容不仅是小学平面图形的重要内容，而且是“图形与几何”领域承上启下的内容，对学生今后学习平面图形有着重要的作用。那么，教师在教学中如何帮助学生积累数学活动经验，渗透数学思想方法呢？课始，教师通过数一数、剪一剪等活动，帮助学生积累转化的经验，使学生明白仅用数方格的方法来探究平行四边形的面积是不够的。然后教师通过多媒体呈现图示（如下），让学生思考为什么要沿着高展开探究平行四边形的面积计算。通过动手操作，学生明白可以将新知转化为已学过的知识进行探究。于是教师提出问题让学生运用转化策略来解答，使学生从中感受到转化策略的价值，促进学生对所学数学知识的理解。最后，教师引导学生回顾与梳理所学知识，巩固学生的记忆。在教师的启发下，除了平面图形中运用到转化策略外，学生还想到了是不是可以将小数除法和乘法转化为整数进行计算。这样教学，学生经历了猜想、验证的过程，积累了丰富的数学活动经验，促进了数学知识的整体建构。

上述教学，教师从面积的概念入手，组织学生进行拼一拼、剪一剪等活动，于无形中向学生渗透转化的思想方法，使学生真正感受到转化策略的实用性，实现了数学知识的整体建构。

综上所述，数学教学中，教师可从知识的整体关联入手，引导学生不断深入探究，促进学生的数学学习，使学生所学的数学知识形成一个有机的整体，实现从整体上提升学生数学核心素养的目的。

（责编 杜 华）