电铲履带系统AdamS ATV动态仿真
2020-07-04邹伟
邹伟
摘要:针对重型履带系统复杂的车辆-地面力学问题,使用Adams ATV模块建立电铲整机模型,准确计算在软地面爬坡、转弯和越障等工况下履带系统的驱动力矩和支重轮受力。爬坡工况下履带系统驱动力矩仿真结果与理论值基本一致,转弯工况下驱动力矩理论值与仿真结果的相对误差在2.5%-26.2%区间;原地转弯所需驱动力矩与12.5°坡角爬坡所需驱动力矩接近。在硬地面越障时,支重轮受力最大值占整机总重力的41.8%。与实际使用值对比结果表明,仿真结果和理论计算值可作为方案设计的参考,且理论计算值偏于保守;各工况计算结果可为动力配置和后继强度设计提供依据。
关键词:电铲;重型履带系统;驱动力矩;支重轮;动力
中图分类号:TP391.92;U469.694文献标志码:B
0 引言
电动机械挖掘机简称电铲,是露天矿山开采系统中最关键的设备之一,其履带式行走装置性能对整机可靠性有重要影响,履带与支重轮、地面之间的复杂力学关系是设计计算的难点。车辆与地面之间的力学建模方法有纯经验法、半经验法、基本理论研究法、模型试验法和计算机模拟法等,其中:半经验法是一种相对简单可靠的建模方法,基本理论研究法和模型试验法的适应性受具体工况限制,计算机模拟法随着计算机硬件配置的提升而迅速发展。与其他半经验计算方法相比,Bekker公式适用性强、计算可靠,特别是在低速载荷工况下适用性更好。王红岩等的试验数据表明,由于履带与地面之间存在滑动,当车辆转弯半径较小时,牵引力或制动力较大。LYASKOL的试验数据表明,履带陷人深度随滑转率增大而增大。
目前,大型商业动力学模拟软件Adams和RecurDyn都使用半经验法中Bekker的载荷一下陷公式计算车轮或履带与地面的相互作用力;Adams软件中的ATV模块可以较准确地计算行驶阻力、履带张紧力等参数。在沼泽、山区等复杂路面高速行驶的履带车辆模拟通常采用用户自研计算机程序计算,通用商业软件模块无法满足需求。在坦克或轻型履带式移动设备方面,业内已有学者和专家使用商业动力学软件进行简单工况下的动力学研究,但在重型履带式工程机械方面尚缺乏分析案例。
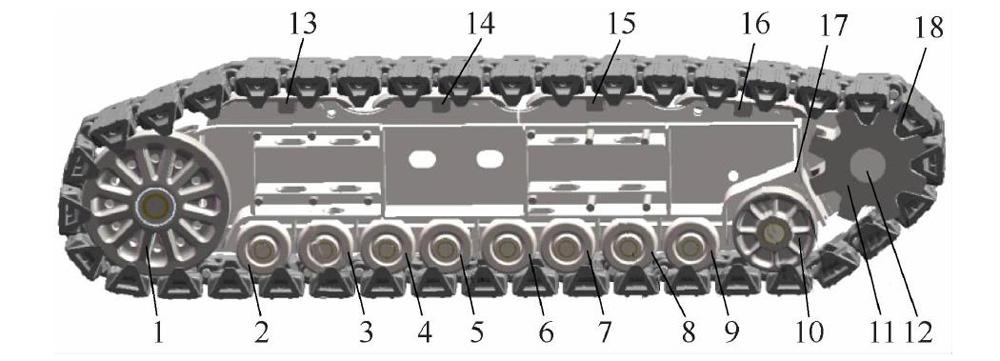
电铲重型履带系统示意见图1。支重轮和滑靴数量较多,各零部件之间以及零部件与地面之间的作用力较大,接触的非线性问题求解难度较大。本文以某型号22m3斗容电铲为例,使用Adams ATV模块进行多工况下的动态仿真,并将仿真结果与Bekker公式等理论计算结果对比,验证模型的正确性并进行后续仿真分析。
1 履带车辆与地面的力学理论
1.1车辆直线行走驱动力矩计算
车辆直线行驶阻力包括履带系统内部摩擦阻力、地面压实阻力、坡道阻力、风阻力和加速惯性阻力等。低速重型履带系统中风阻力和加速惯性阻力占比很小,可以忽略。
考虑支重轮与支重轮轴滑动摩擦、支重轮与履带板侧面滑动摩擦,每个支重轮相关的内部摩擦阻力可表示为
式中:Ci为支重轮i(包括前导轮)上的载荷,N;dbi为支重轮轴i的直径,m;dri为支重轮的直径,m;ur为支重轮和支重轮轴之间的摩擦系数。设Ff为每条履带直线行驶时内部摩擦点阻力,则
驱动轮轴与驱动轮为花键连接,驱动轮轴两端装有滚动轴承,忽略滚动轴承摩擦阻力,则履带平均接地比压为
单条履带直线运行总阻力为
Fd=Ff+Fp+Fs+Fw+Fi(8)
单条履带驱动力矩为
Td=Fdrp(9)
式中:rP为驱动轮的节圆半径。
1.2 车辆平地转弯驱动力矩计算
不考虑履带下陷引起的侧面推土阻力,计算双履带行走装置的转弯驱动力矩。为不失一般性,以左转弯为例,转弯时履带与地面的作用力示意见图2。FqL和FqR为与摩擦力矩相当的直线运行阻力的反方向力,即驱动力;FdL和FdR为直线运行阻力;MfL和MfR为履带与地面之间摩擦力矩。
不考虑履带回转中心偏离其与地面接触面的形心,左、右履带的回转阻力力矩为
2 Adams ATV动态仿真
在Adams ATV模块中建立电铲履带系统模型,见图3。履带系统模型左右对称,左、右两侧均包括前导轮、支重轮、驱动轮、驱动轴、滑靴和履带板,其他部分作为整体机架三维几何实体导人。检查每个构件的质量和转动惯量,确保与实际值一致。履带由Adams ATV模块生成,图3中的箭头所指履带板编号为1,其余履带板编号沿顺时针方向依次加1。
2.1 软地面动态仿真
在露天矿山开采中,电铲一般在重黏土地面上作业,履带会陷入地面一定深度,因此建模过程中将地面视为柔体,将履带系统视为刚体。重黏土地面特性参数设置见表1。
在平地直线行驶工况中,电铲的最大车速为1.25km/h,设置驱动轴转速为27.65(°)/s。编号11的履带板陷入地面深度和接地比压随时间变化曲线见图4。
0-4s为系统自平衡过程,5-8s为加速过程,之后匀速运行。在1-11s,11号履带板陷入地面平均深度为65mm,平均接地比压为309.3kPa;在67-73s,11號履带板陷入地面平均深度为38mm,平均接地比压为300.9kPa。基于静力学计算得到陷入地面平均深度的理论值为67mm,平均接地比压为329.3kPa。匀速运行过程中履带板陷入地面平均深度和平均接地比压均比电铲静止时有所降低。
平地直线行驶时前导轮和支重轮受力曲线见图5。前导轮受力较小,各支重轮受力差异不太明显,支重轮9受力最大,最大值为722kN。
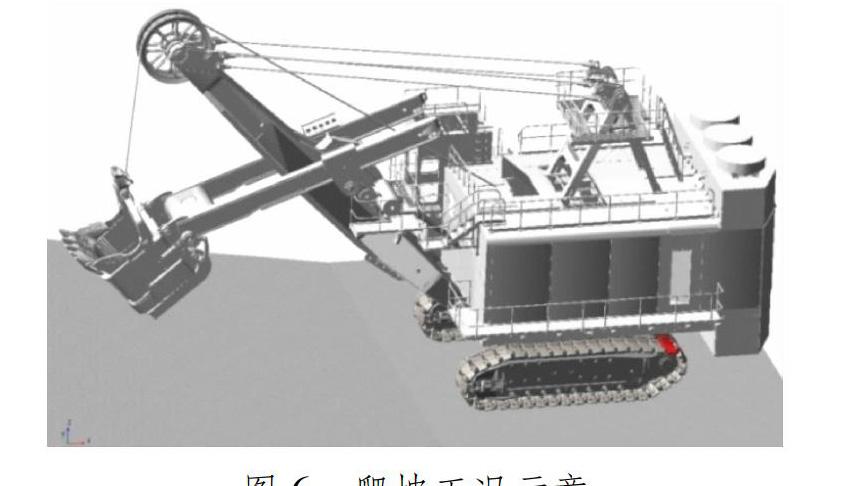
在直线爬坡工况中,电铲的最大车速为0.50km/h,设置驱动轴转速为11.06(°)/S,爬坡工况示意见图6,电铲从平地直线运行上坡。
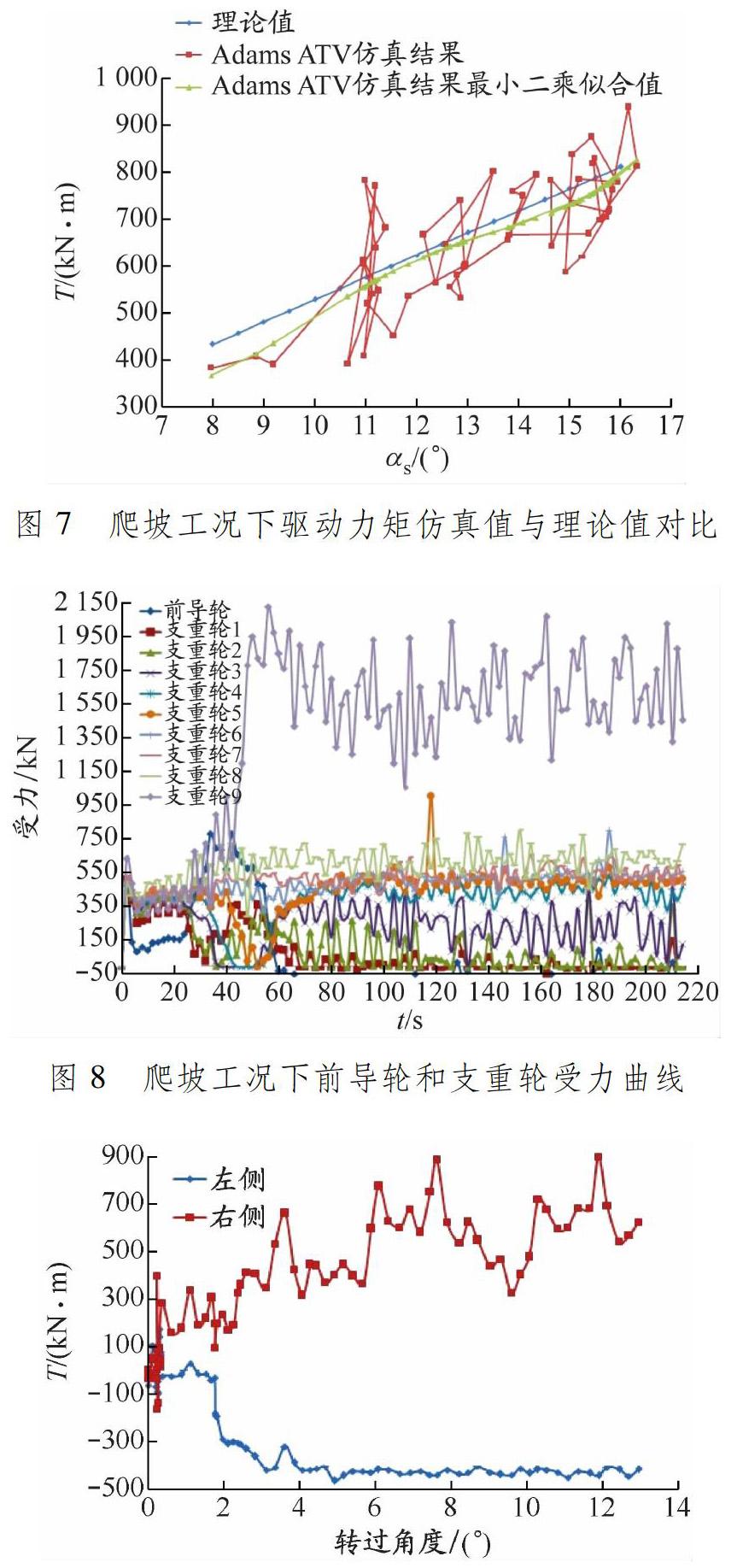
履带系统驱动力矩计算结果见图7。仿真值波动较大,原因是电铲重型履带节距较大(强度要求所需),驱动轮齿数仅为8,运转过程中存在不均匀性。仿真结果的最小二乘拟合值与理论值基本一致,理论值稍微高估驱动力矩,主要原因是运转过程中履带板平均陷入地面深度比电铲静止时有所降低。爬坡工况下前导轮和支重轮受力曲线见图8。不难发现,支重轮9受力较大,最大值为2123kN,占整机总重力的27.6%,因此支重轮9的设计直径明显大于其他8个支重轮直径,以应对受力较大的工况。在平地单侧左转弯工况中,电铲右侧车速为1.00km/h,设置右驱动轴转速为22.12(°)/s,左履带制动。驱动力矩与转过角度关系曲线见图9,转过角度2.5°之内为加速过程,之后左侧平均制动力矩为421.7kN·m,理论计算值为532.4kN·m,理论值与仿真值相对误差为26.2%;右侧平均驱动力矩为549.4kN·m,理论计算值为629.7kN·m,理论值与仿真值相对误差为14.6%,可见理论计算会高估驱动力矩。
在平地雙侧原地左转弯工况中,电铲的右侧车速为1.00km/h,左侧车速为-1.00km/h。驱动力矩与转过角度关系曲线见图10。0-5°为加速过程,之后,左侧平均驱动力矩为797.1kN·m,右侧平均驱动力矩为522.7kN·m,两侧平均值为660.OkN·m,理论计算值为676.7kN·m,理论值与仿真值的相对误差为2.5%;该机型在持续使用中的行走驱动力矩实际值(额定值)为668.0kN·m(传动系统效率来自台架试验数据),三者基本一致。左、右侧驱动力矩仿真值差异的原因是整机重心不在左右对称面上,而理论计算值按整机左右对称计算。与平地单侧转弯工况相比,双侧原地转弯所需驱动力矩更大,表明驱动力矩与转弯半径成反比。平地双侧原地转弯所需驱动力矩与12.5°爬坡所需驱动力矩接近,在方案设计时可以考虑该机型最大爬坡角度设计值为12°左右(矿山规划中电铲爬坡角度通常在9°-13°区间)。
在平地越障工况中,设置地面隆起见图3,隆起高度为250mm,与履带板高度接近;车速为0.50km/h。支重轮2通过后软地面隆起部分被压溃(见图11),软地面越障时前导轮和支重轮受力曲线见图12,支重轮9受力较大,最大值为1852kN。
2.2 硬地面动态仿真
当电铲越过石头等障碍物时,支重轮受力较大,因此分析这类恶劣工况下各支重轮和前导轮受力。设障碍物高度为250mm,地面与履带接触刚度为100000N/mn,n为力指数,取n=2,阻尼为2000N·s/m,车速为0.50km/h。硬地面越障时前导轮和支重轮受力曲线见图13。支重轮在障碍物正上方时受力较大,其中支重轮6受力最大,最大值为3216kN,占整机总重力的41.8%。
3 结论
使用Adams ATV模块可较准确地计算电铲履带系统在软地面爬坡、转弯和越障等工况下的驱动力矩和支重轮受力。在匀速行驶过程中,履带陷入地面平均深度和平均接地比压均比电铲静止时有所降低,驱动力矩的理论计算结果偏于保守;爬坡工况下驱动力矩仿真结果与理论值基本一致;转弯工况下驱动力矩理论值与仿真结果的相对误差在2.5%-26.2%区间。平地双侧原地转弯为行走驱动力矩需求最大的工况,结合整机稳定性工况可以确定最大爬坡角度(本文计算机型合理值为12°左右),行走驱动力矩仿真平均值为660.0kN·m,理论计算值为676.7kN·m,机型配置的实际值(额定值)为668kN·m,三者基本一致。软地面越障时容易将地面隆起部分压溃,硬地面越障时支重轮6受力最大,其值为3216kN,占整机总重力的41.8%,在实际操作中应尽可能避免。
在新机型投入使用后,建议采集驱动电机实际输出参数、爬坡角度和转弯半径等数据,适当转换后与计算值对比,可以改进计算模型,进一步提高动力系统效率。仿真结果证实理论计算值可以作为方案设计的参考,可解决理论计算难以求解重型履带系统超静定问题和比较复杂的地面力学问题的难点,为动力配置和和后续强度设计提供依据。本文方法也可用于其他重型履带系统产品分析。
