关于简单的线性规划的若干思考
2020-07-04刘慈华
刘慈华
【摘要】本文首先阐述了有关简单的线性规划的定义和相关概念,紧接着详细分析了教师在线性规划教学过程中可能遇到的重点、难点问题,并给出了相应的教学策略。最后总结了简单线性规划教学的意义。
【关键词】线性规划 重难点 教学策略
【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089(2020)08-0018-02
一、问题的提出
在组织社会化生产、经营管理活动中,我们经常会碰到最优化决策的实际问题,而解决这类问题的现代管理科学以线性规划为重要理论基础。为了使利用线性规划的方法解决实际问题更加理性化,便于今后我們去解决更多的类似问题,从而产生了一系列的有关概念:线性约束条件、目标函数、线性目标函数、线性规划、可行解、可行域、最优解等。
二、简单线性规划的教学策略
通过对线性规划教学内容及教学过程的研究,我们归纳出线性规划问题数学模型的一般形式:根据题意,列出约束条件及目标函数;画出约束条件所对应的可行域;结合图形,在可行域内找到目标函数的最优解。
通过对简单线性规划的学习,学生对数学建模有了更深的认识,对化归和数形结合的数学思想有更进一步的领悟,同时,学生识图、画图和对图形的分析能力也在进一步加强。但是在教学的过程中,我们应该注意以下三个重难点:1.把实际问题转化成线性规划问题,把文字语言转化成符号语言。解决此难点,要分析实际问题中的已知条件、约束因素、所求问题,列出对应的不等式和目标函数。2.确定二元一次不等式的解表示的是直线的哪一侧区域。解决此难点,可在直线的一侧取一特殊点确定Ax+By+C 的正负,正负与不等式的符号相同,则该特殊点所在的区域为对应不等式所在的区域。3.求线性规划问题的最优解。解决此难点,要结合图形,弄清直线平移时目标函数的取值与直线截距之间的关系。
在教学过程中面临这些困难,我们就要采取相应的对策解决它,一般来说,对于在简单的线性规划中出现的困难,我们应该做到以下几点:
1.题意的理解及条件的转化
题目的条件是什么,有什么限制,要解决什么问题,怎么通过假设把限制条件转化成相应的不等式,把要解决的问题转化成函数。笔者认为要把题意中的文字语言转化成符号语言,要抓住题目中的关健词分析。
例如:某厂打算生产甲、乙两种机械产品,两种产品都需要在A、B两种设备上加工。每台甲产品在A设备所需工时分别为1h,在B设备所需工时为2h;每台乙产品在A设备所需工时为2h,在B设备上所需工时为1h。A、B两种设备每月能使用的时间分别为400h和500h。甲乙两种机械设备每件销售收入分别为3000元、2000元,请问如何安排生产可使收入最大?
这个题目出现次数最多的字眼是甲乙与AB,所以甲乙和AB是关键词,另外,这个题目要我们求的是收入,所以收入也是关健词。另外,收入与甲乙的数量相关,因此,假设显而易见,设生产甲、乙产品分别为x、y台,收入为z元。
怎么列出关于x、y的不等式组与目标函数呢?
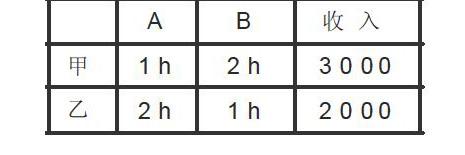
把甲乙和AB的关系及相应的收入列表呈现,相应的不等式和函数一目了然,具体如下:
AB的使用有时间限制,从而x、y的约束条件如下:
x+2y≤400
2x+y≤500
x≥0
y≥0
收入z与x、y有关系,从而得出目标函数:z=3000x+2000y
通过关健词教学法,可以培养学生分析试题的能力。
2.平面区域的作法
画出直角坐标系与直线并不难,至于平面区域的确定,笔者前文已经提及,可以采用特殊点法。但是有些题目要注意直角坐标系的刻度问题。线性规划的问题涉及的都是现实问题,有些量很大,有些量很小,在画图过程中,如果横坐标与纵坐标的刻度一致的话,画起来有一条坐标轴可能很长,甚至很难在纸上操作。因此可根据试题适当调整,如y的范围为1000,x的范围为10,那么y轴上的一个刻度可以是200,x轴上的可以是2。可以适当放缩横纵坐标处理这个问题。
3.目标函数的变形及常规下最优解的找法
在可行域内找到一个点(x,y)使得目标函数最值取到,要完成这件事有很多方法,老教材用的是等高线的方法,让人比较难明白,因为它与以前的知识点联系不是很紧密。现在的教材用的直线平移法。在进行直线平移时,有些学生常常会出错,就是在几条直线之间的位置关系搞不清楚,这可以通过比较直线斜率法加以解决。如让学生掌握k>0,直线的倾斜角为锐角;k<0时,直线的倾斜角为钝角;k>0时,k越大,直线的倾斜角越大;k<0时,k越大,直线的倾斜角也越大。
4.有关整点问题的处理
线性规划中的整点问题就是代入目标函数的点的横坐标与纵坐标只能是整数,不能带有小数,因为要考虑试题中x,y的具体含义。做这类试题可用逐步调整法,如果遇到最优解时的x,y不是整数时,找出离这个x,y最近且解最接近最优解的相应的x,y。
参考文献:
[1]孔繁潜.简单的线性规划[J].数学通讯,2003年第22期.
