一类在磁场中具有调和势的非线性Schrödinger方程解整体存在和爆破的门槛条件

周 凡，黄 娟*，李玉林

（1.四川师范大学数学科学学院，四川成都610066； 2.四川师范大学可视化计算与虚拟现实四川省重点实验室，四川成都610066）

1 引言及主要结果

带磁场的非线性Schrödinger方程是量子力学中描述在非相对论情形下粒子运动状态的方程.因此，对于带磁场的非线性Schrödinger方程解的存在性以及解的相关性质的研究受到许多人的关注.本文考虑如下带磁场的非线性Schrödinger方程：

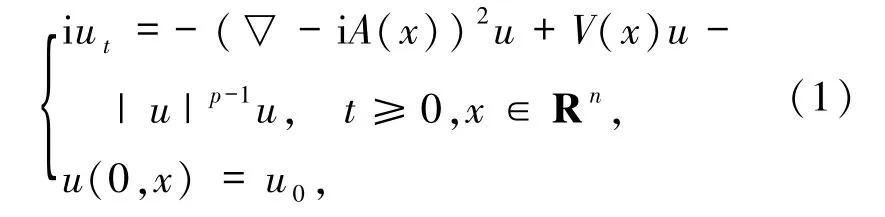
对于方程（1），当 A（x）≠0 且 V（x）=0时，Cazenave 等[1]证明了方程（1）的局部适定性和驻波的稳定性.Cingolani[2]研究了方程（1）的多解的存在性.Tintarev[3]在一般非紧黎曼流形上证明了与哈密顿量有关的方程（1）的基态解的存在性.Bonheure等[4]研究了方程（1）的半经典柱对称解的存在性.Gan等[5]研究了方程（1）在负能量的情况下方程解的爆破条件.Gan等[6]研究在二维磁场中的非线性Schrödinger方程，给出了解整体存在和爆破的门槛条件.Ginibre等[7]研究了方程（1）在与时间相关势函数下的散射理论.当n=2时，舒级等[8]通过能量法给出了方程（1）的解在有限时间内爆破的条件.Ribeiro[9-10]研究初始能量为负时，方程（1）解在有限时间内爆破的条件，以及初始能量为正时整体解存在的条件.

当 A（x）≠0，V（x）≠0 时，文献[11-14]通过压缩映象原理证明了当时方程（1）的局部适定性.Liu等[15]在电势和磁场势的一些衰减和弱对称条件下，证明了该方程具有无限多的非径向复值解.Garcia[16]研究了方程（1）在为任意调和势，V（x）为关于 xr的一阶导数），div A（x）=0，▽A（x）=0 的条件下，且初始能量为负时其解在有限时间内爆破.Cingolani[17]证明了方程（1）的爆破准则.

关于方程（1），本文研究三维空间中（n=3），势函数 V（x）=｜x｜2且

磁场旋转轴 Ω =（ω1，ω2，ω3）（ωi∈R）的情况.考虑初始能量为正且满足一定条件时方程解的整体存在和爆破的门槛条件.具体地，利用方程（1）的哈密尔顿结构建立方程（1）的发展不变流形，研究方程（1）所对应初值问题的爆破解和整体解存在的门槛条件.首先定义如下空间：

其中

当 V（x）=｜x｜2时，方程（1）对应的质量泛函为

能量泛函为

定理1.1若，V（x）=｜x｜2且，初值 u0∈Σ（R3）满足 E（u0）＜B，则：

其中Q是椭圆方程-△Q+Q-｜Q｜p-1Q=0，Q∈H1（R3）的基态解.

注1.1整体解存在的条件可以扩大到1＜p＜5，若初值 u0满足则方程（1）的解 u（t，x）在Σ（R3）中整体存在.

2 预备知识

本文中，在不引起混淆的情况下把积分∫R3·dx 写成∫·dx，A（x）写成 A.

命题2.1（局部适定性[4，11-14]） 设 1 ＜ p ＜5，V（x）=｜x｜2，u0∈Σ（R3），那么方程（1）的唯一解u（t，x）∈C（[0，T]×Σ（R3）），其中 T∈R+是解的最大存在时间.若T=∞，则称方程（1）的解整体存在；若T＜∞，则方程（1）的解在有限时间内爆破.此外，当 t∈[0，T）时，u（t，x）满足 2 个守恒率：质量守恒

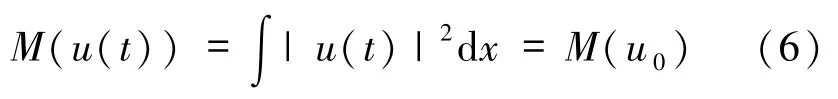
和能量守恒

引理2.1（Heisenberg 不等式[18]）

引理2.2（Gagliardo-Nirenberg 不等式[18]）设1＜p＜5并且Q是非线性椭圆方程的径向对称解

则有如下Gagliardo-Nirenberg不等式

其中

命题2.2[9，16]设 u0∈Σ（R3），且 u（t，x）是t∈[0，T）时方程（1）对应于初值 u0的解，令，且

3 不变流形

设1＜p＜5，定义如下集合：

命题3.1设1＜p＜5，则 Kg和 Kb是方程（1）的不变流形，即如果初始值u0∈Kg（或Kb），则方程（1）的解 u（t，x）仍然满足 u（t，x）∈Kg（或 Kb）.

证明设 u0∈Kg，且 u（t，x）是方程（1）关于初值 u0的解.由命题3.1 知 E（u（t））=E（u0），t∈[0，T），因此，通过 E（u0）＜B，可得

要证 u（t）∈Kg，只需证明

反设（15）式不成立，因为

由连续性可知存在一个t1∈[0，T）使得

现在考虑一个实值函数

F（S）在 S∈R+上满足：

1）当 S=A 时，F′（S）=0；

2）当 S=A 时，F″（S）＜0.

因此，通过（17）和（19）式可知

这与 E（u（t1））=E（u0）＜B 矛盾.因此，（15）式成立.

用类似方法可证Kb也是方程（1）的不变流形.

4 主要结论的证明

定理1.1的证明1）设u0∈Kg，即

当 t∈[0，T）时，由命题3.1 知，方程（1）关于初值u0的解 u（t，x）∈Kg.从而

同时，由

可知结论成立.

2）设 u0∈Kb，即

由命题3.1知方程（1）关于初值 u0的解 u（t，x）∈Kb，即

并且

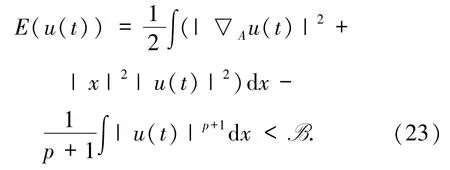
通过引理2.1 和文献[19]知方程（1）的解 u（t，x）在有限时间内爆破.证毕.

通过定理1.1的证明1）可以看出，当1＜p＜5时方程（1）关于初值u0的整体解依然存在.