多向荷载作用下岩溶区嵌岩桩嵌岩深度计算方法

江杰 赖增任 欧孝夺 王智 杨迪

（1.广西大学土木建筑工程学院，南宁 530004；2.工程防灾与结构安全教育部重点实验室，南宁 530004；3.广西防灾减灾与工程安全重点实验室，南宁 530004；4.中铁建设集团有限公司，北京 100040）

目前对岩溶区嵌岩桩嵌岩深度研究多只考虑竖向力或水平力。文献［1-7］基于岩石破坏强度准则，使用不同的力学模型对岩溶区嵌岩桩进行稳定性计算且运用于实际工程中。文献［8-9］开展了不同顶板厚度和溶洞直径下桩端顶板的破坏特征室内模型试验，构建了相应的安全厚度理论计算方法并用有限元软件进行验证。文献［10］通过嵌岩桩荷载传递特性，推导出嵌岩深度的计算方法。文献［11-12］推导了在微小转动下嵌岩段桩侧法向应力及水平摩阻力计算模型，建立了水平荷载作用下公路桥梁桩基嵌岩深度的计算公式。文献［13］考虑基岩顶面水平力和弯矩的共同作用，推导出弯矩和水平力共同作用下嵌岩桩嵌岩深度理论计算公式。上述研究桩体受力与实际工程差别较大，没有对水平力、弯矩、竖向力三向荷载耦合作用下的嵌岩深度计算研究。

因此，本文首先基于Hoek⁃Brown 破坏准则建立水平力、弯矩、竖向力共同作用下岩溶桩基嵌岩深度的函数关系；然后，根据桩底岩石强度推导出水平力、弯矩、竖向力共同作用下嵌岩深度最小值的解析解。根据溶洞安全厚度的验算公式推导出嵌岩深度最大值的解析解；最后联立最小值和最大值的解析解，得出水平力、弯矩和竖向力作用下岩溶区桩嵌岩深度计算公式。

1 嵌岩深度计算

1.1 基本假定

①上覆土层为层状土；②岩层为各向同性均质材料；③岩层中溶洞截面为椭圆形；④上部覆盖土层为均质土且各向同性，各土重度为γi，高度为hi；⑤将上部土自重压力设为均布荷载。

1.2 模型建立与论证

在假定的基础上，本文根据摩尔-库伦弹塑性体模型，忽略嵌岩部分桩身的变形影响，简化应力模型，分析岩溶桩承受水平力、弯矩和竖向力情况下的最小嵌岩深度。岩溶地区嵌岩桩简化的计算模型如图1所示。其中：V为桩顶受到水平力；M为桩顶弯矩；P为竖向承载力设计值；Hs为上部覆盖土层厚度，hr为嵌岩深度；Lmax为L1和L2中的最大值，L1为溶洞顶板拉弯破坏厚度，L2为冲切破坏情况下溶洞顶板厚度；D为桩径。

图1 嵌岩桩力学模型

根据上述假定，由于V和M作用，桩侧岩体产生水平抗力Pu和切向抗剪应力τ，Pu由水平压应力Pn和水平切应力Pτ组成，桩侧岩体的法向最大应力σm，桩侧切向最大剪应力τm，桩上任意一点到桩中心夹角为α，根据文献［14］水平总抗力为两者最大应力矢量在破坏面上的叠加，即

1.3 最小嵌岩深度计算

设桩最大主应力σ1，最小主应力σ3，Hoek⁃Brown提出的广义破坏经验公式［15-17］为

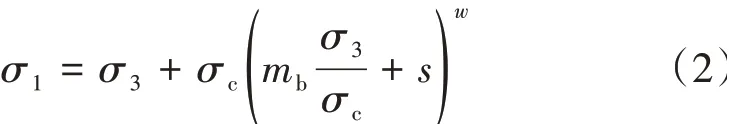
式中：σc为岩石单轴抗压强度；mb为岩体类型；s为完整程度；w为风化程度。

根据广义Hoek⁃Brown破坏法则，mb，s，w计算式为

式中：GSI为地质强度指标；mi为完整岩体的数量；j为扰动系数，取值为0～1，岩体完整时取1。

根据文献［12-13］得到计算结果加入竖向力进行化简整理得

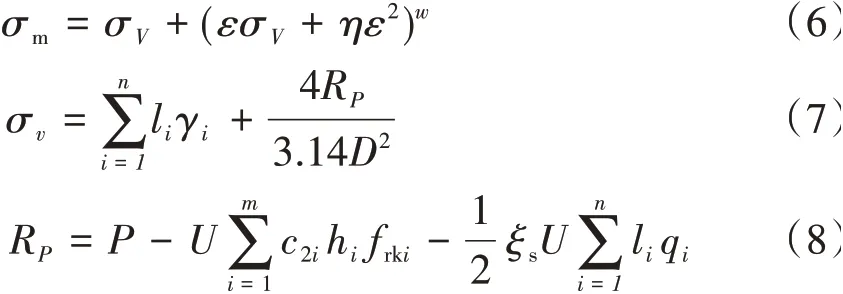
式中：σv为岩石竖向应力；ε为岩体抗压应力的强度模量，ε=mbσc；η为岩体的相对质量，η=s∕mb

2；li为上部土层厚度；qi为上部土层摩阻力；RP为地基受到的压力；U为桩周长；c2i为岩石摩阻力折减系数；frki为岩石摩阻力；ξs为土层折减系数，计算公式参见JGJ 79—2012《建筑地基处理技术规范》。

根据文献［12］得出Hoek⁃Brown 强度准则在低法向应力条件下近似表达式为

式中：σ为岩石破坏法向应力。

当α=0时，σm可视为σ1，而上部荷载产生的σV可视为σ3。α=45°时，τm达到最大值。根据式（1）可得σ为

将式（16）代入式（15），可得τ为

得到基于Hoek⁃Brown破坏准则桩侧岩体的pu为

根据桩体静力平衡条件，则有

式中：c，k为待定系数；A为接触面积；frk为单层岩石摩阻力。

令f1=P-0.1σcA，联立式（13）—式（15）简化得

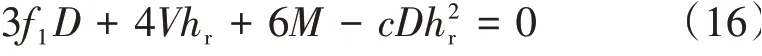
当基岩桩体底部岩体发生破坏时，桩为短桩满足c=pu，化简得到

当竖向力P为0 时，令f1为0，代入式（17）中即可得到无竖向力情况下最小嵌岩深度的解析解。

1.4 最大嵌岩深度计算

在保证嵌岩深度满足条件下，还须保证桩不会对溶洞产生破坏，本文引入嵌岩深度最大值来保证溶洞稳定性。本文主要研究拉弯和冲切情况下溶洞顶板破坏模式。洞室围岩为完整的Ⅰ，Ⅱ级围岩且或较完整有少部分节理裂隙的Ⅲ级围岩时，岩溶顶板简化为矩形宽板且受跨中集中荷载作用，宜按照四边固定边界的矩形板作为溶洞计算模型。矩形板边界条件如图2 所示。两端为双向板受力，图中a，b分别为溶洞短边、长边长度。

图2 矩形板的边界条件

引入荷载分配系数后将双向板转化为单向板计算，对溶洞顶点取矩，水平力V转换为弯矩M2，再与桩顶传递的附加弯矩M3叠加。在自重荷载和多种荷载作用下求解抗拉情况下持力层跨中桩底应力。岩体自重荷载产生的弯矩M0为

式中：q为溶洞顶部荷载，q=γiHb，H为岩层至溶洞顶板的距离。

由于岩石抗压强度约为抗拉强度的10倍，按照最不利情况计算，假定弯矩和均布荷载对溶洞顶板产生拉应力。岩体受集中荷载产生的弯矩为式中：M1为岩石受到的最大弯矩；M2=V·hr（此时hr取嵌岩深度得最小值）；τ2为溶洞顶板破坏切应力；σ2为溶洞顶板破坏压应力；K3为安全系数。

假定岩层节理不发育，岩层结构完整。本文认为溶洞顶板下部的岩体处于受拉状态，岩体内部单元体的形状改变达到了岩体承受的极限应变，岩体发生屈服破坏。

根据材料力学第四强度理论和文献［18］求出荷载分配的方法，把溶洞顶板当作双向板，将其受力简化得到L1，计算式为

式中：K4为安全系数；λ为上部土体和岩石荷载产生弯矩与附加荷载产生弯距的比值；σb为桩端极限应力；σmt为岩体下拉应力，σmt=（0.05～0.02）σc；σ2为溶洞顶板破坏压应力；τ2为溶洞顶板破坏切应力；σm0为岩石和土体产生持力层跨中下缘的弯拉应力；σm1为桩受力传递至跨中下缘的弯拉应力；μ为荷载分配系数。

溶洞顶板冲切如图3 所示，其中θ为冲切角。θ=45°时，桩端岩层将沿节理裂隙面发生冲切破坏。

关于竖向力导致抗剪强度不足的情况，参考文献［18］中公式进行修改。桩端增加土层自重压力和附加弯矩，推导得出L2计算式为

图3 溶洞顶板冲切

式中：τmt为溶洞顶板抗剪切强度，τmt=（0.05～0.02）σc。

1.5 嵌岩深度计算公式

岩溶区嵌岩桩受到水平力、弯矩和竖向力作用时，桩基嵌岩深度必须既满足水平抗力，又保证溶洞顶板不会失稳。H-Lmax即为最大嵌岩深度。结合式（17），嵌岩深度计算取值方法为

2 实例分析

2.1 工程概况

选取南宁市一项目ZJ1 为研究对象，该端承桩的设计嵌岩深度为1 m，岩层至溶洞顶板的距离为8.16 m。该工程地层自上而下为第四系素填土、冲积成因的淤泥质土、残积成因的粉质黏土，二叠系灰岩等。岩溶桩设计资料见表1，溶洞顶板岩体参数见表2，场地土层参数见表3。

表1 岩溶桩设计资料

表2 溶洞顶板灰岩岩体参数

表3 场地土层参数

2.2 岩溶桩嵌岩深度验证

采用文献［18］、JGJ 79—2012 中溶洞顶板厚度设为本文中Lmax，求出岩溶桩嵌岩深度最大值，见表4。

表4 岩溶桩嵌岩深度最大值 m

由表4 可知，JGJ 79—2012 方法中只考虑竖向力情况，计算结果比文献［18］中的计算方法要小6.9%，本文方法比JGJ 79—2012 方法计算值小17.8%。由于本文考虑了弯矩、水平力、竖向力共同作用，本文方法比JGJ 79—2012、文献［18］方法计算值大，因此本文方法更加安全可靠，同时验证了本文方法的正确性。

对于最小嵌岩深度计算方法，JGJ 79—2012 只能计算弯矩、水平力作用下岩溶桩的嵌岩深度，本文方法与文献［12］方法都考虑了竖向力，运用JTJ 285—2000《港口工程嵌岩桩设计与施工规程》中桩基嵌岩深度计算方法，得到岩溶桩嵌岩深度最小值，见表5。

表5 岩溶桩嵌岩深度最小值 m

由表5 可知，本文方法计算的岩溶桩嵌岩深度最小值为0.826 m，文献［12］方法为0.93 m，JGJ 79—2012 方法为0.83 m，JTJ 285—2000 方法为0.75 m。本文计算的嵌岩深度与文献［12］方法、JGJ 79—2012方法、JTJ 285—2000 方法相比误差为12.59%，0.48%，9.20%。同样考虑弯矩、水平力和竖向力情况下，本文最小嵌岩深度比文献［12］计算值更小，在保证了工程安全性的同时又提高了工程经济性。规范中的计算方法未考虑水平力和弯矩的影响，因此本文计算方法比较安全。

3 影响因素分析

根据式（27）可以看出，嵌岩深度与岩面水平力、弯矩、桩径、竖向承载力等因素有关。为了确定最小嵌岩深度受各参数的影响程度，本文取基准条件为：

D=1 m，GSI=50，j=0.6，σc=44.58 MPa。

敏感系数的计算公式为

式中：△P为桩受力参数变化率；Δhr为嵌岩深度变化率。

桩在弯矩M、水平力V、竖向承载力P作用下，岩溶桩基最小嵌岩深度与基岩顶面处桩身竖向承载力的关系曲线见图4。可知：P与M不变时，最小嵌岩深度随V增加呈非线性增加。P和V不变，最小嵌岩深度随M增加呈非线性增加。M和V不变，当嵌岩深度0～0.85 m 时，最小嵌岩深度随P增大而增大；当嵌岩深度为0.85 m 时，随P的增加最小嵌岩深度保持不变；当嵌岩深度超过0.85 m 时，最小嵌岩深度随P的增加呈非线性减小。这是因为三向荷载作用下平均主应力增加，使得土颗粒间的约束和咬合力增强，岩石被压密，导致嵌岩深度最小值随P的增加先增大后减小。

图4 三向荷载作用下最小嵌岩深度变化规律

三向荷载下最小嵌岩深度敏感性见表6。可知：在D和σc相同条件下，当弯矩变化±50%时，敏感度为33%。当水平力变化±50%时，敏感度为15%。竖向承载力变化±12.5%，当嵌岩深度0～0.85 m 时，竖向承载力的敏感性系数随着弯矩和水平力的增加而减小；当嵌岩深度超过0.85 m 时，弯矩对最小嵌岩深度最敏感。

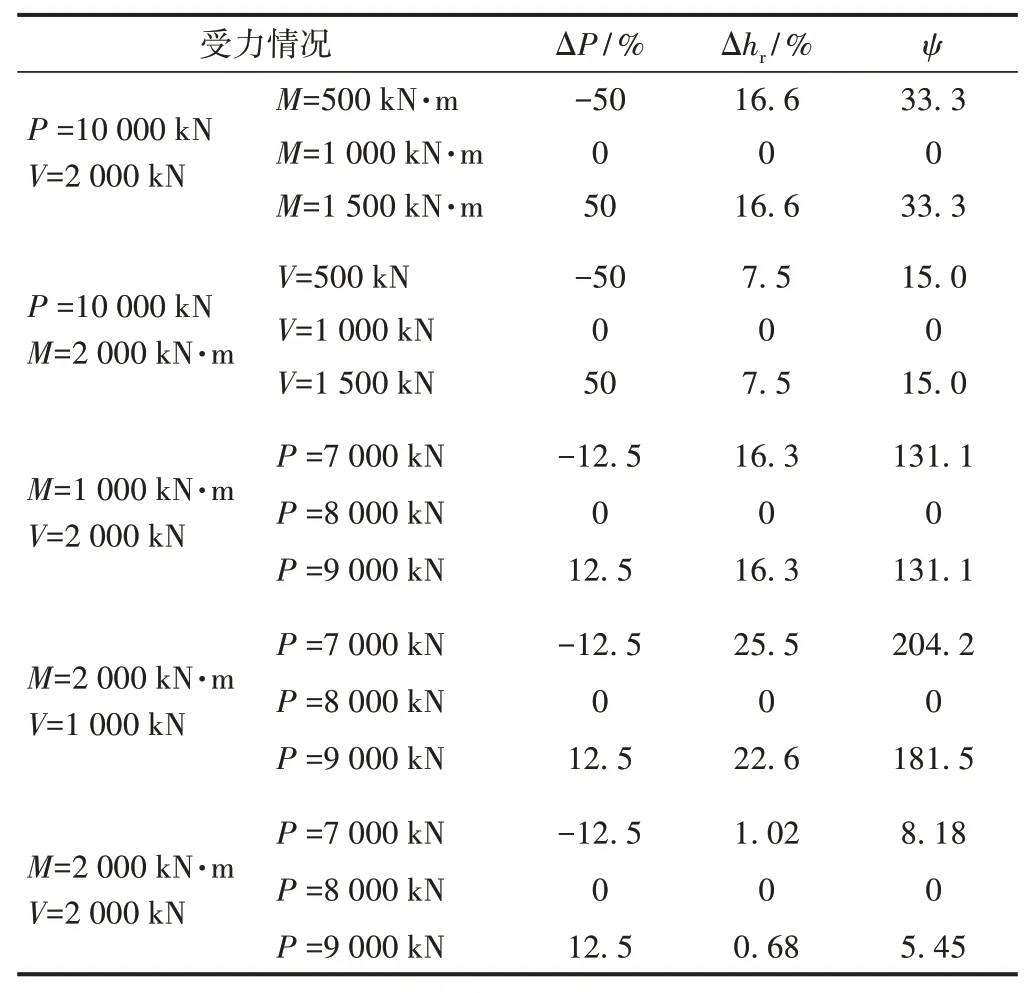
表6 三向荷载作用下最小嵌岩深度敏感性

桩在弯矩M、水平力V、竖向承载力P作用下，岩溶区桩的最大嵌岩深度与基岩顶面处桩身竖向承载力的关系曲线见图5。可知：桩受到M，V不变时，最大嵌岩深度随P增大呈非线性减小；P与M不变时，最大嵌岩深度随基岩顶面处V增大呈非线性减小。P与V不变时，最大嵌岩深度随M增大呈线性减小。

三向荷载作用下最大嵌岩深度敏感性见表7。可知：受力情况对嵌岩深度最大值影响程度存在较大差异。在桩受到三向荷载作用下，竖向荷载对最大嵌岩深度最敏感。

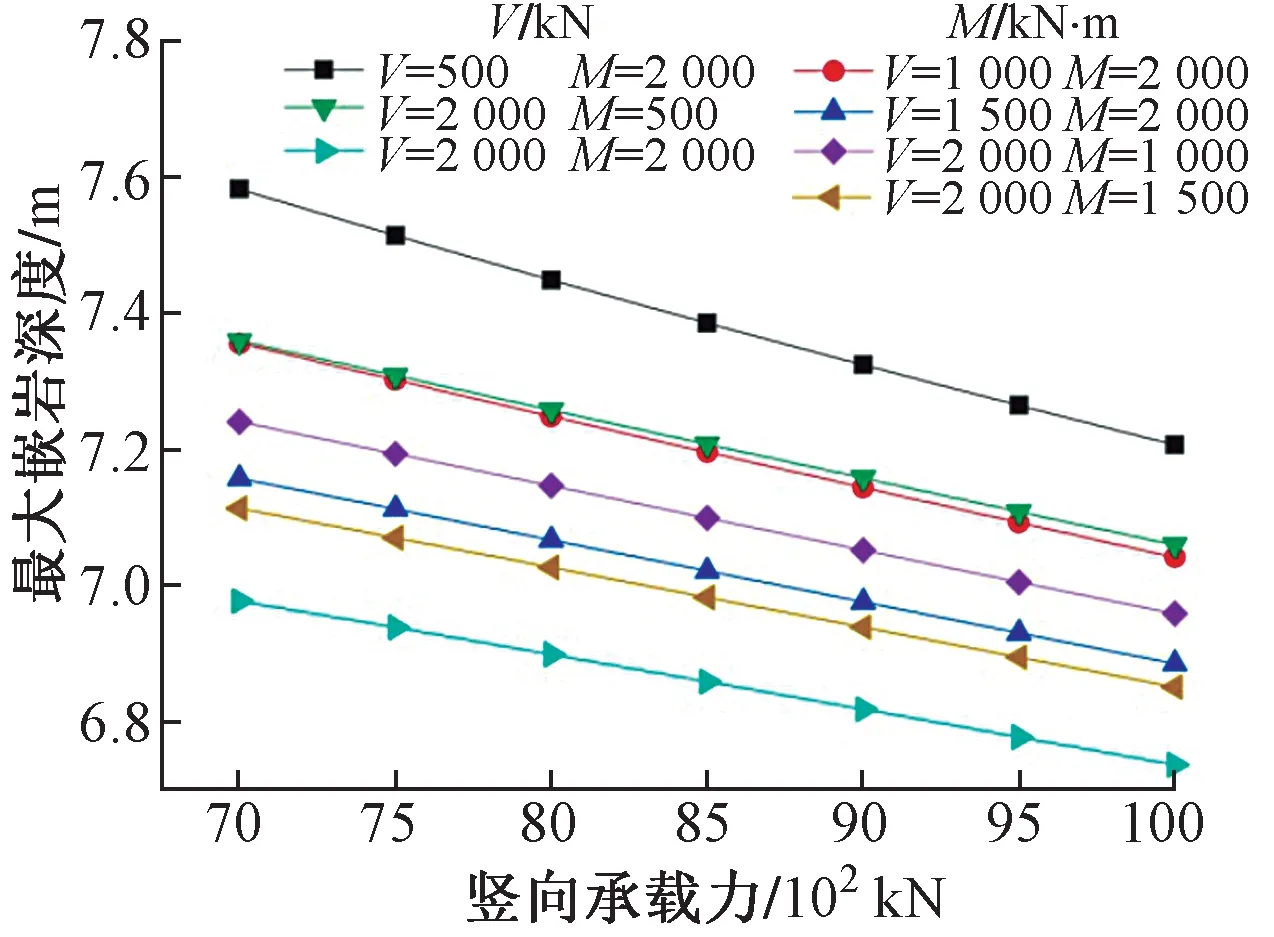
图5 三向荷载作用下最大嵌岩深度变化规律

表7 三向荷载作用下最大嵌岩深度敏感性

竖向承载力、弯矩和水平力越大，桩的最大嵌岩深度越小，溶洞顶板安全厚度越厚。因此，按三向荷载设计桩嵌岩深度时，桩顶竖向承载力越大岩溶区桩的最大嵌岩深度越小，溶洞顶板安全厚度越厚。

4 结论

1）根据Hoek⁃Brown 破坏准则推导出多种荷载下岩溶桩的嵌岩深度解析解。通过引入溶洞破坏准则求得桩端水平力、弯矩和竖向承载力共同作用下冲切破坏的安全厚度、拉弯破坏的安全厚度的理论公式，最后得出水平力、弯矩和竖向承载力共同作用下岩溶区桩的嵌岩深度取值方法。

2）最小嵌岩深度随弯矩、水平力增加呈非线性增大。最小嵌岩深度较小时，先随竖向承载力的增加而增大，当竖向承载力增加到一定值后，最小嵌岩深度随竖向承载力的增加而减小。弯矩对最小嵌岩深度最敏感。

3）在桩受到水平力、弯矩、竖向承载力共同作用时，竖向荷载对最大嵌岩深度最敏感。竖向承载力、弯矩、水平力越大岩溶基桩最大嵌岩深度越小，溶洞顶板安全厚度越厚。