扁平板式吊杆涡振性能及气动优化研究
2020-07-04徐昕宇陈星宇郑晓龙唐浩俊李龙
徐昕宇 陈星宇, 郑晓龙 唐浩俊 李龙
(1.中铁二院工程集团有限责任公司,成都 610031; 2.西南交通大学土木工程学院,成都 610031;3.安徽省交通规划设计研究总院股份有限公司,合肥 230088)
吊杆是中承式、下承式拱桥的主要传力构件,其安全直接关系到桥梁结构的安全性和耐久性。铁路拱桥一般采用刚度大的H 形或矩形断面刚性吊杆。钢吊杆质量轻、阻尼比小,对风的作用较为敏感。尽管涡脱荷载不大,不会使结构发生发散性振动而导致杆件立即破坏,但吊杆本身阻尼较小,在较低风速下易产生一定幅值的共振响应,从而引起吊杆端部连接处的疲劳破坏。
1929 年,美国Tacony Palmyra 桥采用H 形吊杆,通车后不久桥上吊杆出现了风振问题,最后通过加设纵向 抗 风 索 抑 制 了 风 致 振 动[1]。 1973 年,美 国Commodore Barry 钢桁拱桥在建造过程中经历了2 d的风暴后发现9 根H 形吊杆几乎完全断裂,立即采取了节点板连接、在吊杆间设置拉索等措施,而后通过气弹模型试验重现了该桥在18 m∕s风速下的风致振动现象,并在258根桥梁杆件上设置阻尼器,有效地抑制了风致振动,但为此花费了近130 万美元[2]。南京大胜关大桥采用空心矩形钢吊杆的断面形式,经过多次气动优化确定为带倒角的八边形断面,然而在桥梁运营阶段仍出现了吊杆涡振现象,最终通过设置调制阻尼器(Tuned Mass Damper,TMD)抑制了吊杆涡振[3]。
随着桥梁跨度的提高、桥面宽度的加大,拱桥吊杆的长度会进一步加大,而刚性吊杆长细比大、阻尼比小,对风的作用敏感。扁平板式吊杆是一种新型刚性吊杆,仅在欧洲为数不多的几座桥梁上有所应用,国内尚无桥梁应用的实例。扁平板式吊杆的横截面高宽比在1∶4.0~1∶7.5,拱桥最长吊杆在8~32 m[4-5]。
本文针对扁平板式实心吊杆,采用CFD 方法研究不同风向、不同长高比对吊杆断面涡激振动性能的影响,并通过分析流场特征提出2种抑振优化措施。
1 风致涡激振动模型建立与验证
通过流体动力学软件FLUENT,采用Newmark⁃β法编写竖向涡激振动程序,并通过UDF(User⁃defined fuction)在FLUENT 求解器中编译,利用动网格技术实现构件运动的数值模拟。吊杆的运动使流场发生改变,导致作用在吊杆上的力产生变化,从而使吊杆的运动响应发生改变[6-7]。
为验证本文数值模拟计算方法的可靠性,参考已有试验研究[8],采用0.24 m×0.04 m 长方形断面进行CFD 计算分析,结构质量取3.25 kg∕m,频率取5.9 Hz,阻尼比取0.58%,并将计算结果与已有试验结果对比验证。分析采用SSTk-ω湍流模型,此模型结合了适用于近壁面的k-ω模型和适用于远场自由流的k-ε模型的优势[9]。采用SIMPLEC 算法解决N-S(Navier-Strokes)方程中压力和速度的耦合问题。
振幅-风速变化曲线见图1。图中,U为平均风速,m∕s;f为结构自振频率,Hz;D为特征尺寸,m;A为涡振振幅,mm。可知,本文采用的二维数值模拟方法能够模拟断面涡振,涡振的起振风速、涡振最大振幅及其对应的风速均与风洞试验结果(文献[8])吻合。

图1 振幅-风速变化曲线
2 风致涡激振动数值模拟
以高宽比为1∶6的吊杆为研究对象(图2),吊杆网格划分见图3。吊杆模型设置20层四边形正交贴体边界层网格,模型近壁面区域的网格质量细密,计算域内网格总数为31 590。分析时吊杆质量取117.75 kg∕m,结构阻尼比取0.3%。

图2 吊杆短边迎风示意(单位:mm)
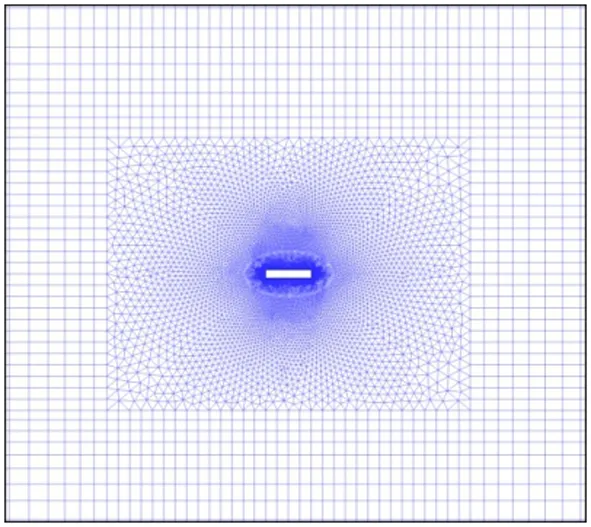
图3 网格划分
由于桥位处风向的不确定性,导致吊杆断面在不同方向上的动力特性有显著差异,风向的改变会引起吊杆的不同振动响应。因此,本文研究长边迎风、短边迎风2种情况。
2.1 长边迎风
吊杆的长度取25 m,其自振频率为2.56 Hz。长边迎风时吊杆涡振数值模拟结果见表1。可知,在来流风速为6.5 m∕s 时涡振振幅最大,其值为35.2 mm。发生最大涡振振幅时升力幅值最大,涡振振动频率与吊杆的自振频率相等。

表1 长边迎风时吊杆涡振数值模拟结果
2.2 短边迎风
由于吊杆截面在2 个方向上刚度差异较大,为使吊杆在2 种迎风工况的频率接近,短边迎风时吊杆长度取10 m,其自振频率为2.54 Hz。通过数值模拟计算,短边迎风时吊杆涡振数值模拟结果见表2。可知,发生涡振时来流风速为1.2 m∕s,涡振振幅为0.4 mm,短边迎风时的涡振振幅远小于长边迎风时的涡振振幅。

表2 短边迎风时吊杆涡振数值模拟结果
3 涡振旋涡脱落规律分析
对长边迎风时的涡脱规律进行重点分析,6.5 m∕s风速下吊杆附近的速度云图见图4。图中0 时刻和2T∕4时刻的位置为平衡位置,1T∕4时刻对应的位置为正向最大位移处,3T∕4时刻对应的位置为负向最大位移处,其中T为1 个涡振周期。可见,在最大涡振振幅对应风速下,由于长边迎风时的挡风面较大,气流受吊杆的阻挡,在上下两端出现明显的旋涡脱落,旋涡的运动范围大,且在吊杆后方产生了巨大空腔。
4 气动措施优化
针对气流在吊杆两侧分离和吊杆后方形成空腔的特点,提出2种气动措施:①在短边两侧增设三角扰流板,扰乱分离后的气流,使旋涡脱落不规律甚至不发生旋涡脱落;②在吊杆上开槽,以抑制吊杆后方产生空腔,扰乱吊杆后方的气流运动。对设置2 种气动优化措施后的吊杆进行长边迎风数值模拟,研究其抑振效果。
4.1 增设扰流板
三角扰流板的截面是边长为70.7 mm 的等边三角形(图5),分布于吊杆两侧,与吊杆短边表面相距50 mm,且沿吊杆纵向每隔一段距离设置连接件,将三角扰流板固定于吊杆上。连接件的设置应保证扰流板与吊杆连接具有足够的刚度,在风荷载的作用下扰流板不会产生较大的自身振动,也不会对吊杆的气动外形产生不利影响。
增设扰流板前后吊杆涡振振幅随风速变化曲线对比见图6。可知:设置扰流板的吊杆仍发生了涡激共振,但涡振锁定区间大幅变小;最大涡振振幅对应风速仍与原始断面的风速基本相同,各风速下涡振振幅均大幅降低,最大涡振振幅由35.2 mm 降低至3.7 mm,振幅减小89.5%。
增设扰流板后吊杆附近的压力云图见图7。对比图4 和图7 可知,设置三角扰流板对吊杆周围流场影响巨大。原始断面后方旋涡稍小,上下侧分离的气流绕过后方贴壁旋涡后就发生脱落。设置三角扰流板后:气流从扰流板与吊杆的缝隙中穿过然后向外流动;吊杆后方很大区域内都形成空腔,旋涡在离吊杆较远的地方才发生脱落;上下侧气流受到扰流板的阻挡同样发生旋涡脱落。

图7 增设扰流板后吊杆附近的速度云图(单位:m∕s)
4.2 吊杆开槽
吊杆竖向开槽位置见图8。竖向开槽前后吊杆涡振振幅随风速变化曲线对比图9。可见,开槽后的吊杆断面在各风速下的竖向位移均接近0,吊杆开槽能够有效抑制涡振的发生。在吊杆上既可通长开槽,也可间断开槽,但设置通长开槽对吊杆的整体性和受力性能会造成一定影响,因此,对吊杆间断开槽可以达到显著减小涡振振幅的效果。

图8 吊杆竖向开槽位置(单位:mm)
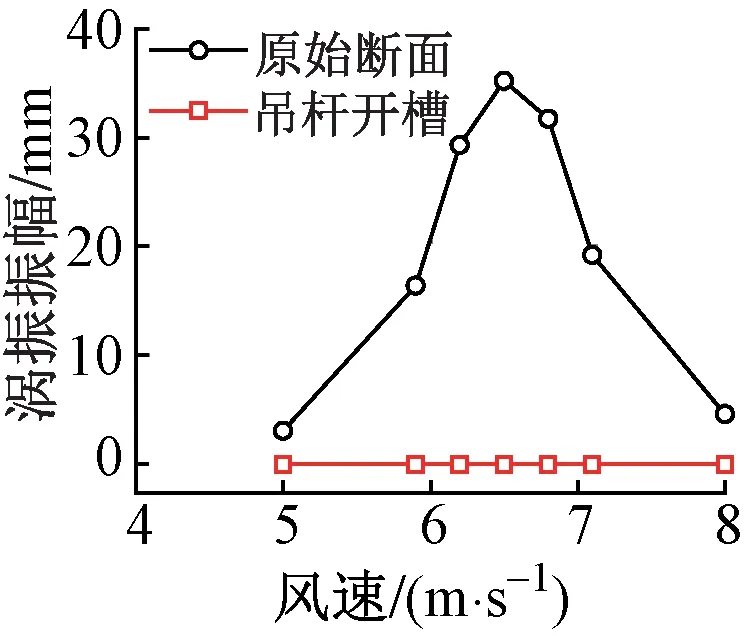
图9 竖向开槽前后吊杆涡振振幅随风速变化曲线对比
开槽后吊杆附近的压力云图见图10。可见,吊杆后方贴壁空腔变小,后方空腔移动至远离吊杆的地方,并在空腔后方发生旋涡脱落,由于距离较远,对吊杆振动影响较小。

图10 开槽后吊杆附近的速度云图(单位:m∕s)
与整体形式吊杆相比,开槽后的吊杆风致涡振性能良好,但中央开槽可能对吊杆的受力产生一定影响,因此在设计吊杆的开槽位置时,应对吊杆应力进行检算。
5 结论
1)建立了风致涡激振动模型并与试验数据对比,验证了数值模拟方法和模型的可靠性。
2)原始扁平板式吊杆断面在长边迎风时,最大涡振振幅为35.2 mm,对应来流风速为6.5 m∕s;在长边迎风时最大涡振振幅为0.4 mm,对应来流风速为1.2 m∕s。发生最大涡振振幅时,涡振振动频率与吊杆的自振频率相等。
3)长边迎风涡振振幅最大时,由于吊杆的挡风面较宽,旋涡的运动范围大,气流在吊杆的上下侧出现明显的来流分离和旋涡脱落,并在吊杆后方产生巨大空腔。长边迎风时,扁平吊杆表现出更明显的钝体特性,吊杆上下侧旋涡的周期性脱落以及吊杆后方的巨大空腔是引起扁平吊杆涡振的重要因素。
4)设置三角扰流板能够明显减小吊杆上下侧脱落旋涡的尺度,吊杆虽然发生了涡激共振,但涡振锁定区间大幅变小,最大涡振振幅对应风速仍与原始断面的风速基本相同;各风速下涡振振幅均大幅降低,最大涡振振幅由35.2 mm 降低至3.7 mm,振幅减小89.5%。
5)吊杆竖向开槽后,吊杆后方的气流较为紊乱,空腔得以大幅度减小,吊杆断面在各风速下的竖向位移均接近0,表明吊杆开槽能够有效抑制涡振的发生。
