改进版拉普拉斯锐化的水下图像增强方法研究

沈建文

(云南昆船电子设备有限公司，云南 昆明650000）

目前，水下图像处理技术已经有着广泛的应用[1]。例如：某研究所研究人员对深水或潜水下生物的研究、军用或部分民用水下特殊搜救、 水下武器系统及水下探测应用等。 由于水本身带有的特殊性质、光学特性以及水中悬浮物的存在，都对水下图像有一定的影响。 如：造成图像的对比度差、图像颜色的失真等问题[2]，这使得水下图像后期处理中的图像进行增强越来越受到重视[3]。

本文提出了一种改进版拉普拉斯锐化的水下图像增强方法。 利用拉普拉斯锐化能够锐化图像、清晰图像边缘的特点，在拉普拉斯算子上利用直方图均衡化灰度等级拉伸的思想，设置增强率，提高图像对比度；最后，利用对比实验进行验证，实验表明本文算法很好的综合了成像质量与运行时间实现了对图像的增强。

1 基本原理

1.1 水下图像问题分析

水下图像处理问题的关键点在于：

1.1.1 由于海水中悬浮物使图像的分辨率受到影响，导致图像模糊，细节分辨较差，辨识度不高；

1.1.2 海水的吸收作用，会使图像各通道的衰减程度各异而导致色彩失真，当光照条件不好，会产生图像对比度下降，部分受影响的图像细节将更差。 对于上述的一些难点， 需要采用图像增强技术处理一些图像的细节问题和对比度。

这些问题对图像进行特殊处理均有非常大的影响， 如对采集的水下图像进行分割处理、水下特殊目标识别等，这使得水下图像后期处理中的图像进行增强越来越受到重视。

1.2 拉普拉斯图像锐化简介

拉普拉斯图像锐化方法，原理可以描述为：当邻域中心像素灰度（ 以X 表示）低于它所在的领域内其它像素的平均灰度（ 以Y 表示）时，降低中心像素灰度；当X 高于Y 时，提高中心像素灰度，此方法可实现水下图像的锐化处理。

2 改进后的拉普拉斯锐化的水下图像增强方法

借鉴直方图均衡化灰度等级拉伸的思想， 以拉普拉斯变换为载体，提出改进版拉普拉斯锐化法，对水下图像进行处理。

拉普拉斯锐化，计算如式(1)所示。

由公式（ 1）经过离散化处理并通过一阶差分公式得到：

公式取反和变形后可得到4 邻域和8 邻域的拉普拉斯卷积核，分别为：

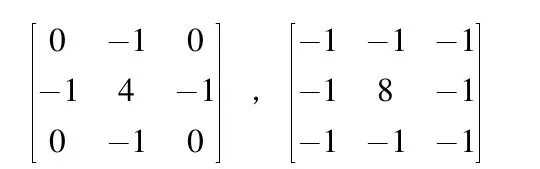
对原图像的边缘进行了锐化处理。

处理卷积核：

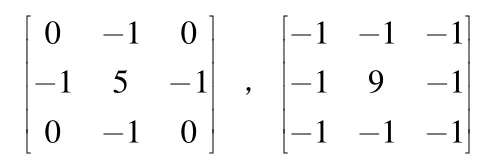
采用8 邻域为卷积核对图像进行锐化处理，如式（ 3）所计算：

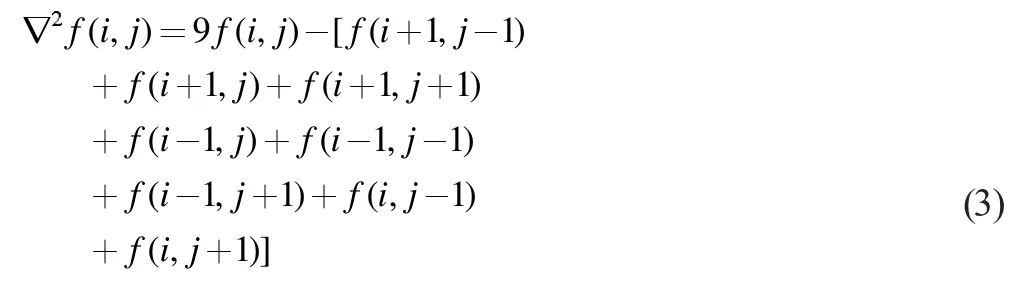
将上述的思想，改为如下形式：

在此增强率用 α表示，从上述公式可得出，通过调节 α，能将所求的中心像素得到增强， 起到和直方图均衡化相同的作用，使图像的对比度得到提升。

算法中的增强率 α的取值取决于所处的环境，环境越亮，α的值越小，反之则越大，具体的场景决定之后， α会被赋予一个初值，以目标的检测结果为导向，当目标无法检测到时，通过循环迭代 α来不断提高增强率。 再通过设定一个阈值来限制 α的迭代，此时仍然检测不到，则目标检测失败。

3 对比实验

如图1，选取三种不同天气，不同时间拍摄的三种场景来表示光线强度的三个不同等级， 图1 中，b、c、d 顺序为直方图均衡、Retinex 增强和本文采用算法增强的效果图。 通过分析，用一个正比于所有熵的定义的公式进行分析讨论，具体见式4。

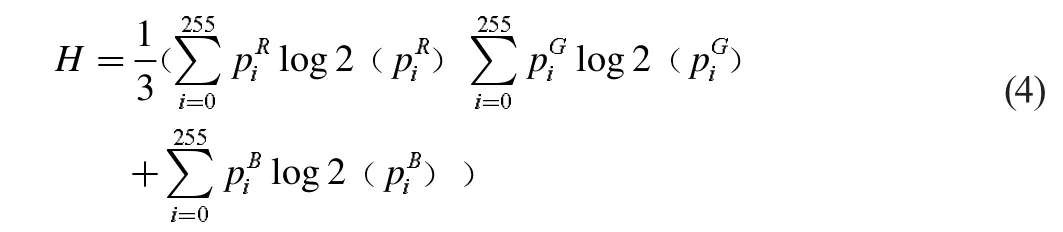
式中，

R——红色通道表示。

由（ 4）式可得，对于彩色图像，需要对它的各个通道分别求取图像熵，采用加权来得到结果。

图1 算法对比

式中，

δ( i , j)——灰度差：相邻像素间；

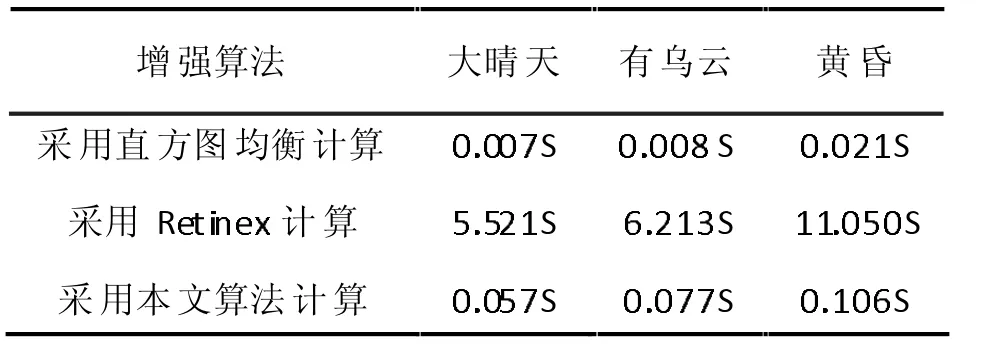
表1 对比平均运行时间

对表1 分析可知，图像越暗，算法需要处理的时间则越长。其中采用Retinex 最耗时，效果不错，但是不能满足实时刷新的要求；采用直方图均衡最快；本文采用算法运行时间是直方图均衡的10 倍左右，为Retinex 算法的1/100 左右，处理时间0.1s左右。 本文算法较直方图均衡化、Retinex 综合效果更好。

4 结论

本篇文章提出了一种改进版拉普拉斯锐化的水下图像增强算法，使对不同环境的图像在保证细节边缘的同时，结合直方图均衡化对图像整体对比度增强明显的特点，使得水下图像得到合理的增强；同时 α随外界光照条件进行自适应调节，提升了算法的使用范围。通过将其与直方图均衡化和Retinex 算法进行对比分析，发现综合成像质量与运行时间，本文算法水下图像增强效果更好。