基于冻结磁导率法的内置式永磁同步电机的转矩精确的分离
2020-07-03杨庆凤
杨庆凤
(金陵科技学院机电工程学院, 南京 211169)
0 引 言
内置式永磁电机的转矩有两个来源,一是由永磁体和电枢作用产生的永磁转矩,另一个则是由于电机和转子凸机引起的磁阻转矩。从电机设计的角度来说,增大磁阻转矩可以有效地提升电机的转矩密度和过载能力,同时可以扩宽电机的弱磁恒功率运行范围。因此,对内置式永磁电机来说,如何准确的分析其磁阻转矩显得尤为重要[1]。
现有文献已提出多种分离磁阻转矩的分析模型,其中包括恒定永磁磁链[2-3]、永磁磁链仅随q轴电流变化[4-5]、冻结磁导率法的引入[6-7]。前两种方法无法正确地将永磁磁链从d轴磁链中分离出来,这是因为负载情况下的电机系统是非线性的,叠加原理不再适用。而冻结磁导率法可以适用于非线性情况下的转矩分离。但是目前基于冻结磁导率的转矩分离大都是集中在平均转矩上,并非是瞬态电磁转矩。
因此,本文提出一种利用冻结磁导率的瞬态电磁转矩分解方法。该方法可以考虑不同负载下d轴和q轴磁路的磁饱和,有效地将电磁转矩进行不同转矩分量的瞬态分解。此外还发现,由于定子铁心饱和带来的d轴和q轴的磁阻不同也会产生一部分转矩分量。
1 解析模型
1.1 传统模型
永磁电机的磁饱和随着负载的变化而变化。轻载时电机的磁饱和较弱,d轴和q轴的磁路是相互独立的,相互之间的交叉耦合可以忽略不计。因此,d轴和q轴的磁链方程为
ψd=ψm(id,iq,θ)+Ld(id,iq,θ)idψq=Lq(id,iq,θ)iq
(1)
1.2 本文提出模型
但是,当电机在重载时,d轴和q轴的磁路会严重饱和,此时d轴和q轴的的交叉耦合就必须要考虑。必须指出,式(1)已经可以部分考虑d轴和q轴的磁路交叉耦合,因为ψm,Ld和Lq同时d轴电流和q轴电流相关。但是该模型并没有考虑d轴电流对q轴磁链的贡献和q轴电流对d轴磁链的贡献。通过简单的有限元分析可得:假如给电机施加一个较大的正的d轴电流,保持q轴电流为零,产生的q轴磁链并不为零。为了考虑交叉耦合带来的影响,在磁链数学模型中引入d轴和q轴之间的互感为
ψd=ψmd(id,iq,θ)+Ld(id,iq,θ)id+Mdq(id,iq,θ)iqψq=ψmq(id,iq,θ)+Mqd(id,iq,θ)iq+Lq(id,iq,θ)iq
(2)
电磁转矩的计算通常有两种方法,麦克斯韦应力张量法和能量法。由于麦克斯韦应力张量法对网格剖分和积分面的选取比较敏感,本文选择能量法来计算电磁转矩。
dq轴坐标系下,永磁电机的转矩表达式如式(3)所示。将式(2)代入式(3),可得式(4)。可以看出电磁转矩由多个转矩分量叠加而成。
(3)
(4)
但是式(4)并不能直接用于冻结磁导率进行转矩分量的分离,因为式(4)没有考虑到由于冻结磁导率下磁共能引起的转矩。为了能够精确分离各个转矩分量,本文提出一种新的转矩模型:
(5)
式中,Tmr为由于定子铁心饱和带来的d轴和q轴磁阻差异与转子永磁磁场相互作用产生的转矩分量。图1给出的是内置式永磁电机在额定负载下转子位置为0°和7.5°时的相对磁导率分布图,明显可以看出两幅图中在定子铁心上d轴的相对磁导率要大于q轴。d轴和q轴的磁阻不等会和转子永磁磁场相互作用产生转矩,即便电枢绕组不施加电流。这体现在式(5)中的Tmr。本文所研究的对象是一台24槽4极的内置式永磁电机,相应的电机参数如表1中所示。
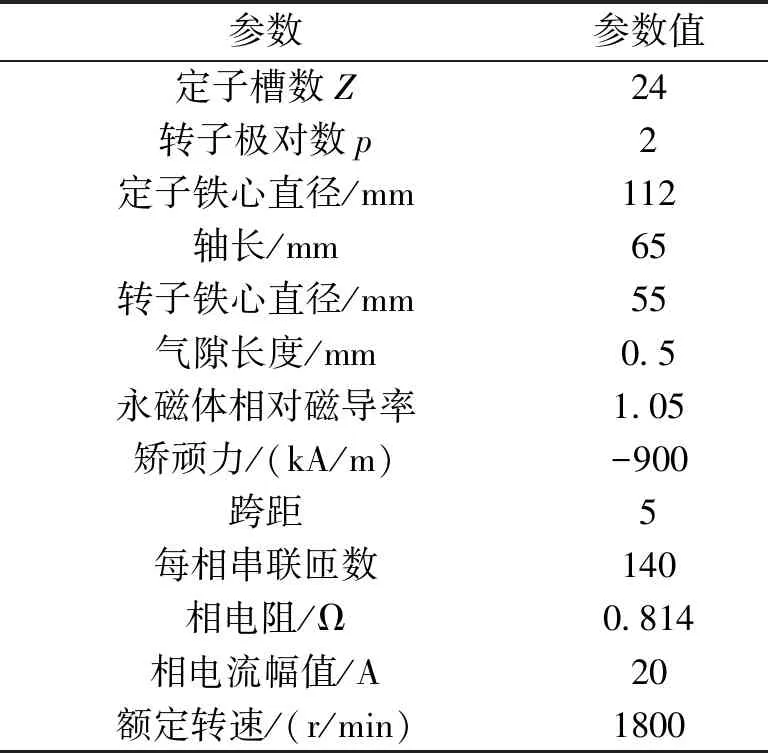
表1 内置式永磁电机参数表

图1 永磁电机在额定负载下不同转子位置下的冻结磁导率
2 基于冻结磁导率法的转矩精确分离
2.1 冻结磁导率法
冻结磁导率法可以用图2所示的B-H曲线来进行说明,其中下标“PM”、“i”、“combined”分别表示永磁体励磁、电枢电流励磁、二者同时励磁。二者同时励磁时的磁力Hcombined是永磁磁力HPM和电枢磁力Hi的线性叠加。永磁体励磁、电枢励磁和永磁电枢同时励磁时的在B-H曲线上工作点分别用“a”、“b”、“c”来进行表示,对应的磁密用BPM、Bi和Bcombined分别表示。明显可以看出BPM+Bi>Bcombined,这表明永磁和电枢的合成磁场并不是永磁磁场和电枢磁场的线性叠加。
利用冻结磁导率法可以将永磁和电枢共同作用时的冻结磁导率固定在μcombined。也就是说冻结磁导率下电机的B-H曲线不再是非线性的,而是一直斜率为μcombined的直线。此时永磁体和电枢作用时的工作点分别由“d”、“e”表示,此时的磁密分别为BPM_FP、Bi_FP。可以看出,此时合成磁场Bcombined等于BPM_FP和Bi_FP的和。因此在冻结磁导率下,线性叠加原理仍然是适用的。

图2 冻结磁导率法示意图
2.2 基于冻结磁导率法的不同激励下转矩的计算
利用冻结磁导率法,通过在一个电周期中进行一系列同激励下的转矩计算,可以将各个转矩分量从式(5)进行分离。具体的实施的过程如图3所示。

图3 基于冻结磁导率法的转矩计算流程
首先,在有限元里计算电机在某一工况下的一个电周期里的磁场。在这一个电周期里,每一个转子位置下,电机定子和转子铁心的每一处的相对磁导率都会被保存下来。因此,再施加电流进行仿真时,此时的定转子铁心材料的每一处的B和H的关系将有保存得到的相对磁导率决定。因此,为了得到式(4)的各个转矩分量,电机的激励源根据表2的分为6种。那第一种激励情况来说,为了得到此时的转矩,将永磁体的剩磁设为0同时保持电枢电流不变来进行有限元计算。在表2的6种激励情况下电机的转矩都计算完毕后,将进行下一个转子位置的计算,而定转子铁心的相对磁导率也会根据之前所保存的数据进行更新,直到一个电周期计算完毕为止。

表2 不同激励源下的转矩分量
2.3 转矩分量的分离
额定工况下,表2所示的内置式电机的各个转矩分量的瞬时值如图4所示。表3给出了各个转矩分量的平均值。可以看出转矩分量“B”对平均转矩的贡献最大,因为其包含了永磁转矩分量。转矩分量“A”对平均转矩的贡献也很大,因为其包含了磁阻转矩分量。由于d轴和q轴交叉耦合引起的转矩分量“C”和“E”相对较小。同时必须指出由于转子永磁体和定子铁心饱和导致的凸极相互作用产生的转矩是负值。
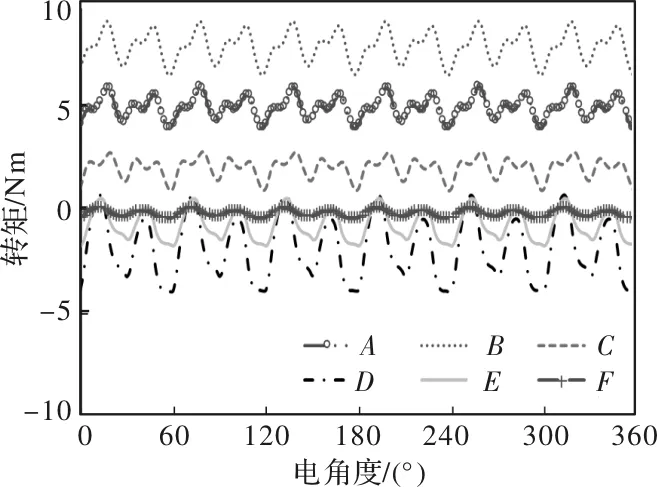
图4 各个转矩分量瞬时值随转子位置变化图
表3 各个转矩分量的平均值
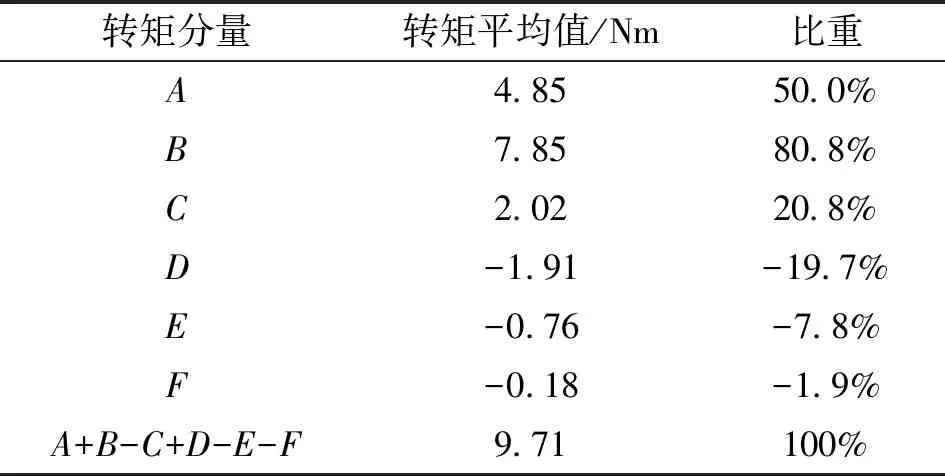
转矩分量转矩平均值/Nm比重A4.8550.0%B7.8580.8%C2.0220.8%D-1.91-19.7%E-0.76-7.8%F-0.18-1.9%A+B-C+D-E-F9.71100%
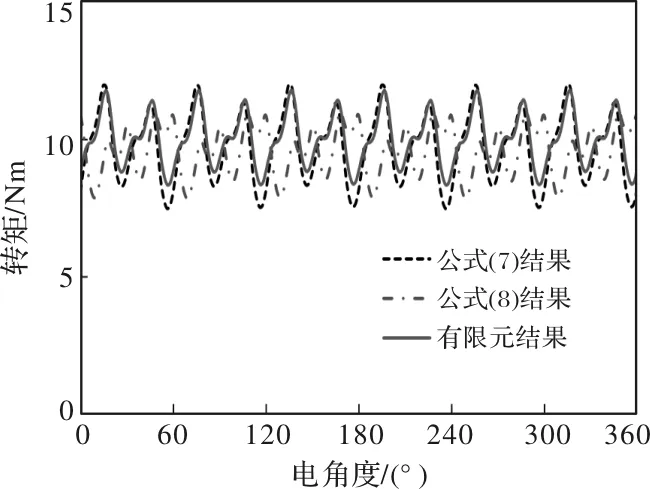
图5 各个转矩分量瞬时值随转子位置变化图
由式(5)和各个转矩分量的关系可知,电磁转矩可以表示为式(6):
Tem=A+B-C+D-E-F
(6)
为了验证所提出的转矩分离方法的正确性,将由式(6)所计算得到的电磁转矩和由有限元仿真得到的转矩进行比较,如图5所示。可以看出所提出各个转矩分量的叠加和仿真得到的结果十分吻合,验证了式(5)的正确性。
(7)
另一方面,传统的转矩计算方法,如式(7),也可以通过表2的各个转矩分量叠加得到。但是由式(7)计算得到的转矩存在较大的误差,如图5所示。这是由于该方法没有考虑到磁路饱和下d轴和q轴的交叉耦合。
3 磁阻转矩的分离
在这一小节,将会对磁阻转矩的分离基于传统转矩公式和本文所提出的转矩公式进行比较。
由传统转矩模型计算的磁阻转矩为
(8)
基于本文所提出的模型的磁阻转矩为
(9)
图6为由式(8)的传统模型和式(9)的本文提出模型仿真得到的磁阻转矩波形。表4列出了磁阻转矩的平均值和所占转矩比重。可以看出传统模型计算得到的磁阻转矩的平均值小于本文提出的模型计算的结果。这是由于传统模型忽略了由于d轴和q轴交叉耦合引起的转矩分量“C”和“E”。

图6 磁阻转矩波形的比较
表4 磁阻转矩的比较

磁阻转矩传统方法本文方法平均值/Nm3.594.85比重37%50%
4 结 论
本文提出了一种电磁转矩的分解方法,通过该方法,结合冻结磁导率可以有效地进行转矩分量的分离。该方法可以实现任何负载下电磁转矩的再现,和传统的磁阻转矩分离方法相比较,本文的方法能够更精确地评估内置式永磁电机的磁阻转矩分量。
