基于混沌粒子群算法的铜转子异步电机优化

胡 堃，庄海军，魏 蜜，廉国明

(中国矿业大学 电气与动力工程学院，江苏 徐州 221116)

0 引 言

近年来能源日益匮乏、环境污染日益严重，进一步的节能减排以及环境保护刻不容缓，异步电机在各行各业应用广泛，这也要求异步电机朝着超高效和超超高效率的方向发展。异步电机采用铜转子结构，可以在原有的设计上，大大提高电机效率，达到IE4的标准，但是铜转子电机也带来很多问题，因此对铜转子电机进行优化设计具有一定的理论意义和工程价值。

目前，在工艺上解决了铜转子铸造的问题，使得异步电机普遍采用铜转子成为可能。相比常规异步电机，铜转子异步电机具有低损耗、高效率、低温、高可靠性、振动小、噪音小等优点，但是采用铜转子也带了很多问题，比如起动转矩变小、起动电流变大。文献[1]提出了铜转子起动的问题，并重新设计齿槽来满足起动要求，提出了深槽、窄口型的齿槽能很大程度上提高起动转矩和降低起动电流；文献[2-3]从优化定、转子齿槽的角度来改善起动问题；文献[4-5]提出田口算法，从转子槽众多尺寸里合理选择优化的参数；文献[6-7]提出响应面来代替有限元仿真，将目标拟合成曲面，节约优化时间；文献[8-9]提出遗传算法来进行多目标优化；文献[10-11]提出粒子群算法来进行多目标优化。上述文献提出的全局算法求极值，局部收敛效果较差，收敛时间比较小。

结合上述研究的观点，本文提出混沌粒子群算法，在基本粒子群的基础上，加入混沌理论和权重因子，加快收敛时间。利用田口算法来确定优化参数，将优化目标利用响应面法拟合成曲线，对铜转子异步电机进行多目标优化。旨在满足电机其他性能指标的前提下，改善电机起动性能。

1 利用田口算法来确定电机优化参数

1.1 田口算法的基本理论

田口算法是由日本专家田口玄一提出的，这是一种基于正交实验和信号比的局部优化算法，其最大的优点在于利用最少的实验次数来达到确定参数的目的。

1.2 电机的基本参数

基于22kW、4极的三相异步电机，电机参数如表1所示,其剖面图如图1所示。

表1 三相电机的参数

图1 铜转子异步电机的剖面图

1.3 参数的水平值

起动电流的公式：

(1)

起动转矩的公式：

(2)

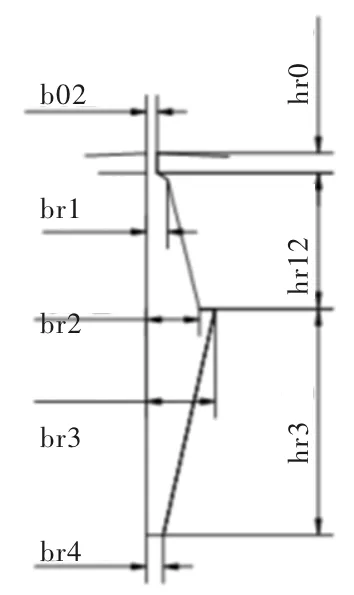
图2 转子槽的槽形

图2为凸型槽，这种槽型槽口小、槽深，会增强电流的肌肤效应，使转子导体电阻增加、槽漏抗减少；最终会促使起动转矩增大，改善起动性能。为了进一步分析转子槽结构参数的改变对电机性能指标的影响，将b02、br2、br3、hr0、hr12、hr3作为参数因子。参数因子的水平值的具体选择如表2所示。

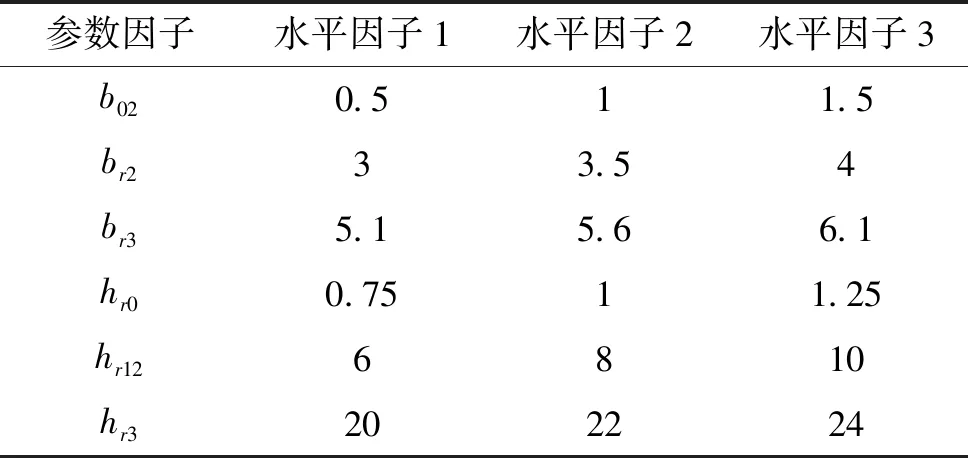
表2 参数因子及水平值

1.4 田口算法的实验结果

在传统的电机设计优化中，若是进行参数化扫描，参数每更改一次就需要重新进行一次有限元计算。若本次设计采用传统方法，则需要进行36次；利用田口算法建立正交表，只需要27次实验，大大减少了计算量，提高了优化的效率。正交实验结果如表3所示。

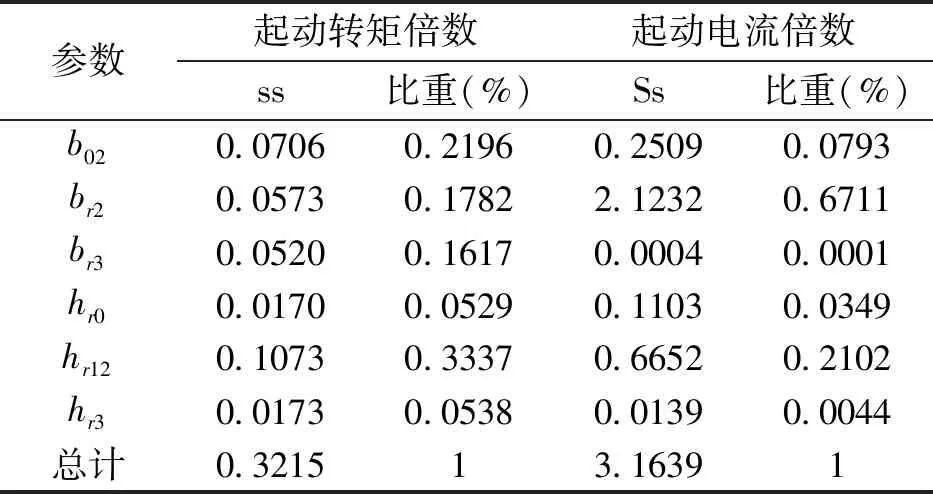
表3 各个参数对性能指标影响所占的比重

通过计算与分析，可以获得转子槽变量对电机起动转矩倍数和起动电流倍数的影响权重比，由上表3，我们可以看出b02,br2,hr12对电机优化目标的影响比较大，因此选择这几个结构变量来作为下一步多目标优化的参数。

2 利用响应面构造目标函数

2.1 响应面的原理及函数的选择

响应面[10]的基本思路：在假象的函数形式上，将有限元计算得到的若干样本点拟合成结果曲线，并使实验结果与所假设的函数误差最小。

在建立响应面模型的过程中，必须选择函数y的具体函数形式使拟合后的函数能够使拟合结果更精确。

在经典响应面算法中，通常选择全区域线性或二次多项式的形式:

线性型：

(3)

不含交叉项的二次项：

(4)

含交叉项的二次型：

(5)

在本次实验中，响应面有弯曲的趋势，所以采用交叉项的二阶模型。

2.2 响应面的参数水平

对于存在曲率的响应面，一般采用中心复合设计和Box-Behnken。在本次实验中，采用的是Box-Behnken方法能够利用较少的试验次数拟合出准确的响应面，Box-Behnken方法采用三水平设计，其参数设计水平如表4所示。

表4 响应面参数的水平值

2.3 响应面的结果

令b02为X(1),br2为X(2),hr12为X(3),目标函数起动转矩倍数为Kst、起动电流倍数为Ist，其式(6)～式(7)如下，拟合曲线如图3～图4所示。

Kst=-0.39364+0.40461*X(1)+1.03215*X(2)+0.008356*X(3)-0.00116*X(1)*X(2)+0.00356*X(1)*X(3)-0.01125*X(2)*X(3)-0.93285*X(1)2-0.092595*X(2)2+0.005438*X(3)2

(6)

Ist=5.68831+0.76751*X(1)+2.0782*X(2)-0.56926*X(3)+0.02148*X(1)*X(2)-0.003112*X(1)*X(3)+0.06114*X(2)*X(3)-0.18965*X(1)2-0.19098*X(2)2+0.01913*X(3)2

(7)

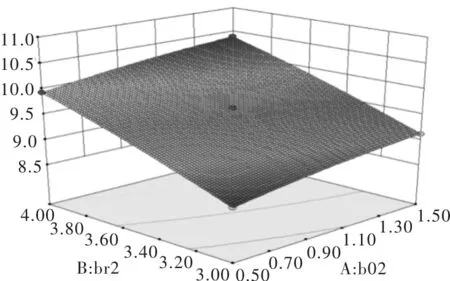
图3 起动转矩倍数拟合曲线

图4 起动电流倍数拟合曲线

3 混沌粒子群算法

3.1 基本粒子群的原理

粒子群优化(PSO)算法[11]是模仿鸟类的觅食行为，将问题的搜索空间比于鸟类的飞行空间，将每只鸟抽象为一个无质量无体积的微粒，用以表示问题的一个候选解，优化所需要寻找的最优解则等同于鸟寻找的食物。该算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。

在基本微粒算法中，微粒的飞行速度直接影响着算法的全局收敛性。速度过大，能保证各微粒很快飞行全局最优解的区域。但当逼近最优解时，由于微粒飞行缺乏有效的控制与约束，很容易飞跃最优解，转去其他区域，从而很难收敛到全局最优。所以，算法的速度缺乏有效的控制时，不具备较强的局部搜索能力。为有效控制微粒飞行速度，Shi和Eberhart在算法模型中引入了惯性权重系数w,以实现对微粒飞行速度的有效控制与调整。微粒的速度和位置表达式变为

vi,j(t+1)=wvi.j(t)+c1r1[pi,j-(t) ]+r2[pg,j-xi,j(t)]

(8)

xi,j(t+1)=xi,j(t)+vi,j(t+1),j=1,…,d

(9)

针对PSO算法容易早熟以及算法后期易在全局最优解附近产生震荡现象，可以采用线性变化权重，让惯性权重从最大值wmax线性减少到最小值wmin。随算法的迭代次数的变化公式为

(10)

式中，wmax,wmin分别为w的最大值和最小值，t为当前迭代步数，tmax为最大迭代步数。

3.2 混沌优化算法的原理

混沌是存在非线性系统中的一种较为普遍的现象。混沌并不是一片混沌，而是有着精致内在结构的一类现象。混沌运动具有遍历性、随机性、规律性等特点，能在一定范围内按其自身的规律不重复地便利所有地状态。最重要的是，混沌地遍历性特点可被用来进行优化搜索而且能避免陷入局部最小，这与全局搜索算法存在明显区别，无疑会比随机算法更具优越性。

混沌的定义：

设V是一个紧的度量空间，连续映射f:v-v如果满足下列三个条件：

(1)对初值敏感依赖：存在δ>0和任意x,在x的ε邻域内存在y和自然数n，使得d(fn(x),fn(y) )>δ。

(2)拓扑传递性：对于V上的任意一对开集X、Y,存在k>0,使fk(x)∩Y≠Ø。

(3)F的周期点集在V中稠密，则称f是在Devaney意义下V上的混沌映射或混沌运动。

3.3 混沌粒子群算法

当粒子群算法处于早熟，可以由多种方法解决这个问题，其中一中方法就是混沌搜索，即采用混沌粒子群优化算法。

混沌粒子群是在基本粒子群算法上的改进：

(1)对初始化种群进行混沌优化，并选出性能较好的种群规模的粒子作为初始种群。

(2)对个体最优或全局最优位置进行混沌优化，当搜索出个体最优或全局最优后，采用混沌迭代的方式，保留性能最好的个体随机取代当前群体中的个体。

(3)引入线性变化权重因子，解决算法后期的震荡现象。

3.4 粒子群与混沌粒子群算法的对比

为了比较两种算法的优越性，用两种算法对同一曲线求极值，以此来说明混沌粒子群的优势。

例如对于下列对象：

(11)

分别用两种算法进行求解极值，其中粒子数取40，c1=c2=2,wmax=0.9,wmin=0.4,混沌迭代次数取20，粒子群迭代次数取100，适应度-迭代次数曲线如图5所示。

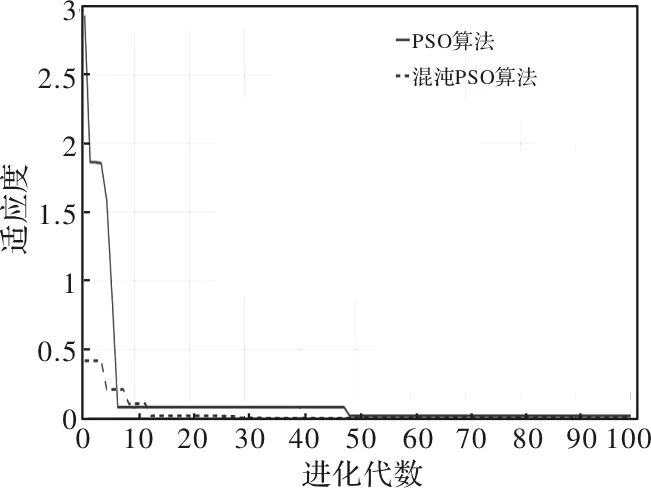
图5 两种算法的适应度曲线

可以看出，混沌粒子群与基本粒子群相比，在收敛速度上有明显的优势。

3.5 混沌粒子群的优化

在多目标规划问题时，常用的方法有约束法、评价函数法、功效系数法，其中最常用的是评价函数法，评价函数法又分为理想点法、平方和加权法、线性加权和法、乘除法、极大极小法。在本次实验中，由于起动转矩倍数求最大值，起动电流倍数求最小值，是两种极值问题，所以我们选择线性加权和法来构造多目标函数。

(12)

然后构造评价函数：

(13)

一般情况下，权系数的值由各目标函数fi(x)的重要程度给出。

在本次设计中，起动转矩倍数要最大，起动电流倍数要最小。由响应面求取的起动转矩倍数和起动电流倍数，先求取相应的下届，因为起动转矩倍数要最大，所以 将起动转矩倍数取倒数求极小值，在取倒数求得最大值。

Kstmax=2.87,Istmin=8.63

权重系数w1=w2=1,构造下面的目标函数：

minf(x)=(kst-2.87)2+(Ist-8.63)2

(14)

基于混沌粒子群搜索算法实现铜转子异步电机多目标优化，从图6可以看出，经过130次迭代达到最优；其参数和性能结果如表5～表6所示，可以看出优化之后的电机性能完全满足国家标准且性能提高明显。

表5 电机参数优化前后比较

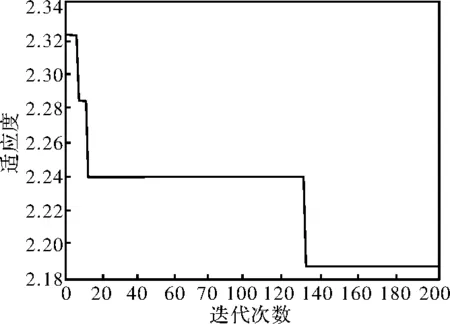
图6 混沌粒子群的适应度曲线

表6 电机优化前后性能比较

性能参数标准限制优化前优化后起动转矩倍数≫1.872.520292.61154起动电流倍数≪9.369.632859.08201

图7和图8分别是优化前后起动转矩和电流的曲线对比，实线为优化前，虚线为优化后。可以明显的看出，起动转矩升高，起动电流明显降低。大的起动电流会造成较大的线路压降，影响接在同一变压器上的其他负载的正常运行；对于频繁起动的电机，大的起动电流也会造成电机内部发热过多而损坏电机 ，经过优化之后，降低了起动电流，延长电机使用寿命且不会影响其他负载的正常运行。

图7 优化前后起动转矩比较

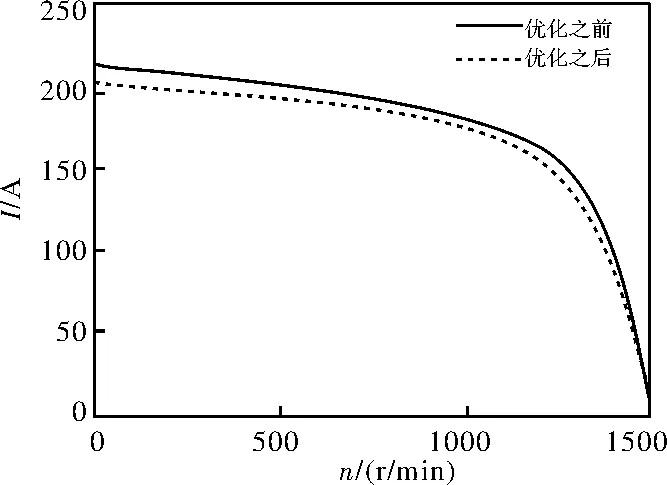
图8 优化前后起动电流比较

图9为电机在稳态运行时的磁密分布，从图中我们可以看出，稳态时齿部和轭部磁密都未超过此硅钢片的饱和值，所以此次优化设计是符合电机设计的要求。

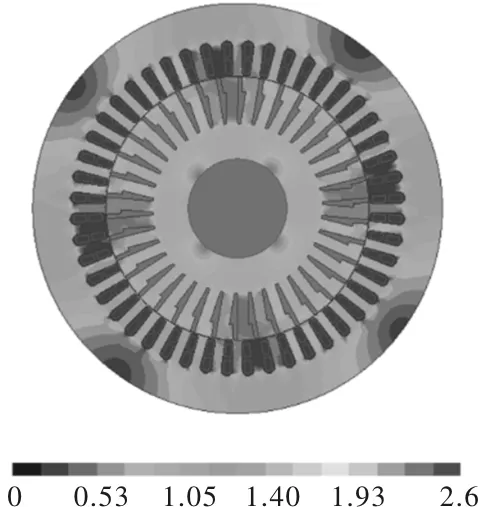
图9 电机稳态的磁密分布

4 结 语

本文针对铜转子异步电机，带来的起动转矩变低、起动电流升高的问题，提出混沌粒子群算法从电机结构上进行优化，来改善电机的起动性能。首先利用田口算法从转子槽众多尺寸中选择对性能影响比较大的参数作为优化参数，再利用响应面将目标函数拟合成曲线，最后利用混沌粒子群算法对目标曲线求极值，得到优化之后的电机参数。混沌粒子群算法在收敛速度上明显比基本粒子群算法要快，并且能很好的解决多目标函数的极值问题。优化之后的电机，在其他性能指标符合国家标准的基础上，起动性能得到改善，对改善铜转子电机起动性能的研究，具有一定的参考价值。