主从机械手遥操作双边自适应阻抗控制策略
2020-07-03张建军吴中华刘群坡王红旗刘卫东
张建军, 吴中华, 刘群坡, 王红旗, 刘卫东
(1. 河南理工大学 电气工程与自动化学院,河南 焦作 454000; 2. 西北工业大学 航海学院, 西安 710072)
主从机械手遥操作双边系统解决了因距离限制使操作者直接处于危险区域的问题,实现了人机智能交互[1].从机械手位于工作区域直接与操作对象交互,跟踪主机械手的运动信号并将与环境交互力信号传送至本地主机械手,使操作者在操作本地主机械手的同时能够感知从机械手传送至本地的力信息[2].然而,主从机械手具有非线性特征、参数的不确定性[3]、关节摩擦[4]、外部干扰以及通讯时延问题[5].此外,操作者和远端环境分别与主从机械手交互影响机械手数学模型.远端从机械手运动过程受到阻力等不确定扰动,难以获得机器人数学模型,且无法通过线性系统的伺服控制理论设计控制器.不确定遥操作控制在保证整体系统稳定性的前提下,提高透明性及鲁棒性,将位置、力信号同步地在主、从机械手上复现,依然是整体控制目标[6].
假设操作者与被操作对象无源,主从遥操作系统可以看作外环、实现主手(全文主手即主机械手)力跟踪、内环从手位置跟踪的双闭环控制系统.其控制主要有基于力反馈[7]以及位置反馈[8]两种反馈方式,实现主手与从手(全文从手即从机械手)力和位置的协同一致.为了解决遥操作控制中存在的模型不确定及外部干扰等问题,国内外很多学者提出了不同的控制方法[9-10].针对机械手双边遥操作系统从手不确定干扰问题,Park等[11-12]提出了从手阻抗控制与积分滑模消除从手不确定干扰问题并实现了力位移跟踪,但未考虑主手关节摩擦以及外部不确定问题.郭语等[13]针对主手的不确定问题,提出了主手端扰动观测器的双边阻抗控制下的自适应控制.然而其控制律设计以质量-阻尼线性系统为基础,对于二维竖直平面受到重力影响存在控制不确定性.Sharifi等[14-15]在主从机器人考虑非线性动力学模型,针对关节摩擦引起的模型不确定问题,提出了自适应双边控制方法并应用到康复训练遥操作过程中,但是没考虑外部干扰引起的不确定问题.针对速度不可测以及不确定动态方程问题,Yang[16]提出了基于速度观测器的神经网络不确定补偿的鲁棒滑模控制,实现了主从手力位置同步.
通讯时延是影响遥操作控制性能的关键问题,很多学者对固定时延以及可变时延做了深入研究.然而,对于如排雷排爆、水下遥操作、核辐射区遥操作等双边遥操作系统,由于距离较近通讯时延影响可以忽略不计,此时模型不确定性以及外部干扰引起的问题更为明显.本文针对主从机械手双边遥操作过程中动态模型不确定及外部干扰问题,提出了双边自适应阻抗控制策略.通过建立线性二阶微分方程的参考阻抗模型,将主从手参考阻抗模型的动态响应期望位置作为主从机械手末端的操作空间下的位置跟踪目标,并且设计了主从手控制律.通过自适应调节补偿参数的不确定性,针对外部干扰,设计了自适应上界估计率,利用基于滑模控制的自适应律来抑制不确定误差及外部干扰作用,实现了模型不确定性及外部干扰下的鲁棒性能.所设计的控制律无需获知双机械手的准确数学模型以及主从机械手的不确定干扰上界,只需要保证主从手力测量的准确性,主从机械手位置和关节长度的准确测量,即可实现主从手力位移跟踪渐进收敛特征.
1 数学模型及基本属性
n自由度主从机械手关节空间非线性动力学模型为[17]
(1)
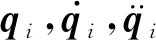
(2)
式中:Ωi(qi)为关节空间下关节位置qi与操作空间下末端位置xi的函数关系.设xi与qi同维,即设机械手为非冗余,Ji(qi)=dΩi(qi)/dqi为非奇异矩阵.将式(2)代入式(1),整理可得机械手在操作空间的动力学方程:
(3)
结合式(1)与(3)可得:
(4)
上述非线性机械手系统具有以下属性[18-19]:
属性1机械手惯性矩阵Mi(qi)与Mxi(qi)正定,且有上下界.
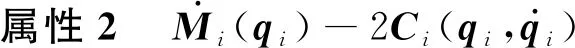

属性4根据未知参数不同,机械手动力学模型可以线性化为
(5)

2 整体控制策略
本文提出的基于参考阻抗模型的自适应双边控制框图如图1所示.ximm,xims分别为主、从机械手阻抗模型输出的期望位置.为了实现主机械手上的人机交互以及从机械手目标抓取过程交互,设计了两种阻抗模型.在该控制方案中,主手通过操作者作用力与环境力建立阻抗模型获取期望的主手位置,通过鲁棒自适应控制律及外部误差上界估计实现基于阻抗模型的期望位置跟踪.从手通过环境力与主手位置建立期望的阻抗模型,通过鲁棒自适应调节控制律及自适应上界估计实现从手对从手期望阻抗位置跟踪.基于阻抗模型的参考自适应阻抗控制的目标是基于关节摩擦及外部干扰等引起数学模型不确定的前提下,保证主从手力-位置跟踪的稳定性及收敛性.

图1 遥操作双边自适应阻抗控制结构图
3 控制器设计
阻抗控制通过调节用户设定的目标阻抗模型使机器人末端实现柔顺性运动,将阻抗控制加入自适应特征,使在外界不确定条件下主机械手触觉力跟踪从手触觉力信号具有鲁棒性能.在自适应阻抗控制实现过程中,将设计的阻抗控制模型作为参考模型,通过设计控制器和自适应律使被控对象闭环动态模型逼近参考模型.在提出的阻抗遥操作系统中,定义了两种阻抗模型根据主手上与人的交互以及从手与环境的交互过程,主从机械手期望阻抗模型设计如下[20]:
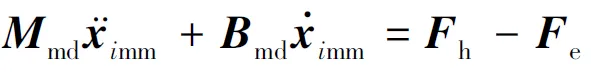
(6)
(7)




(10)
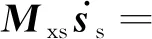
(11)

(12)
(13)
证明:选取李雅普诺夫函数为
(14)
由于Mxm、Mxs正定,很显然V0>0.对式(14)求V0关于时间的一阶导数,将式(10)、(11)及相应控制律(12)、(13)代入,可得

(15)
定理1证明完毕.然而,实际应用中主从机械手控制器无法保证动态方程参数以及外部干扰信号全部已知,基于τmeq、τseq设计不确定条件下的主从手操作空间控制律为
(16)
(17)


(18)

(19)
(20)
(21)


(22)
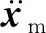
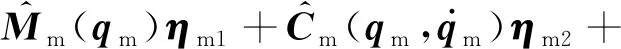
(23)

(24)

(25)
(26)
主从机械手的自适应律设计为
(27)
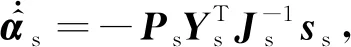
(28)
式中:Pm、Ps为正定对角矩阵.
4 稳定性证明

证明:选取李雅普诺夫函数为
V1=Vm+Vs
(29)
(30)
(31)

(32)

(33)

(34)

(35)
由式(33)、(35)与(29)可得
(36)
对式(36)不等式两端积分可得


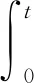
(37)

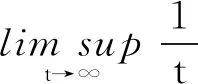

(38)

5 仿真与验证
从机械手跟踪主机械手运动过程中,分为自由空间运动以及与环境接触约束运动[24,25].建立从机械手抓取目标的受力模型,只考虑运动位置对Fe的影响,从机械手在与环境接触时,环境受力看成无源的线性弹簧,一维空间下,接触力Fe可以表示为
(39)
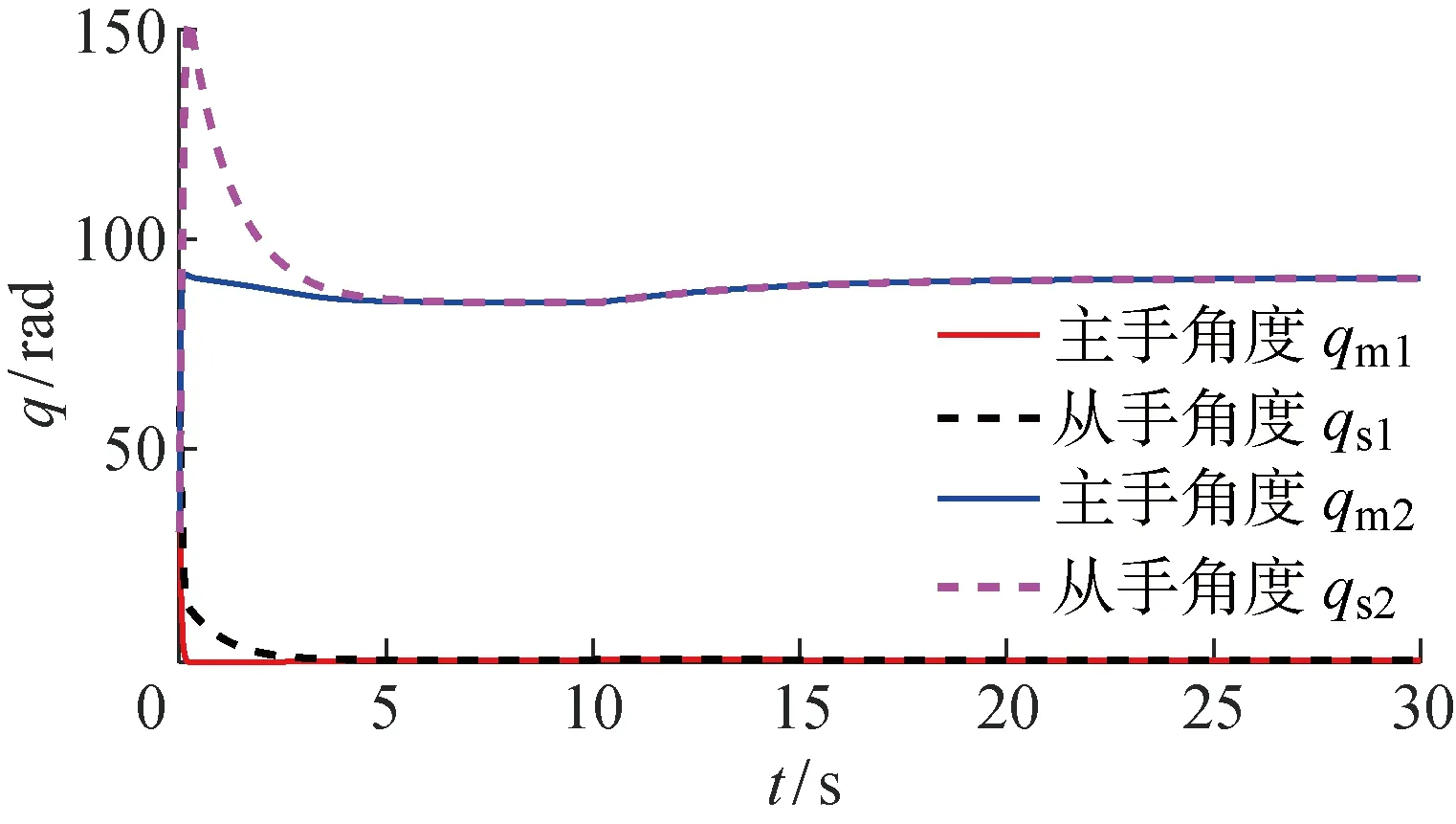
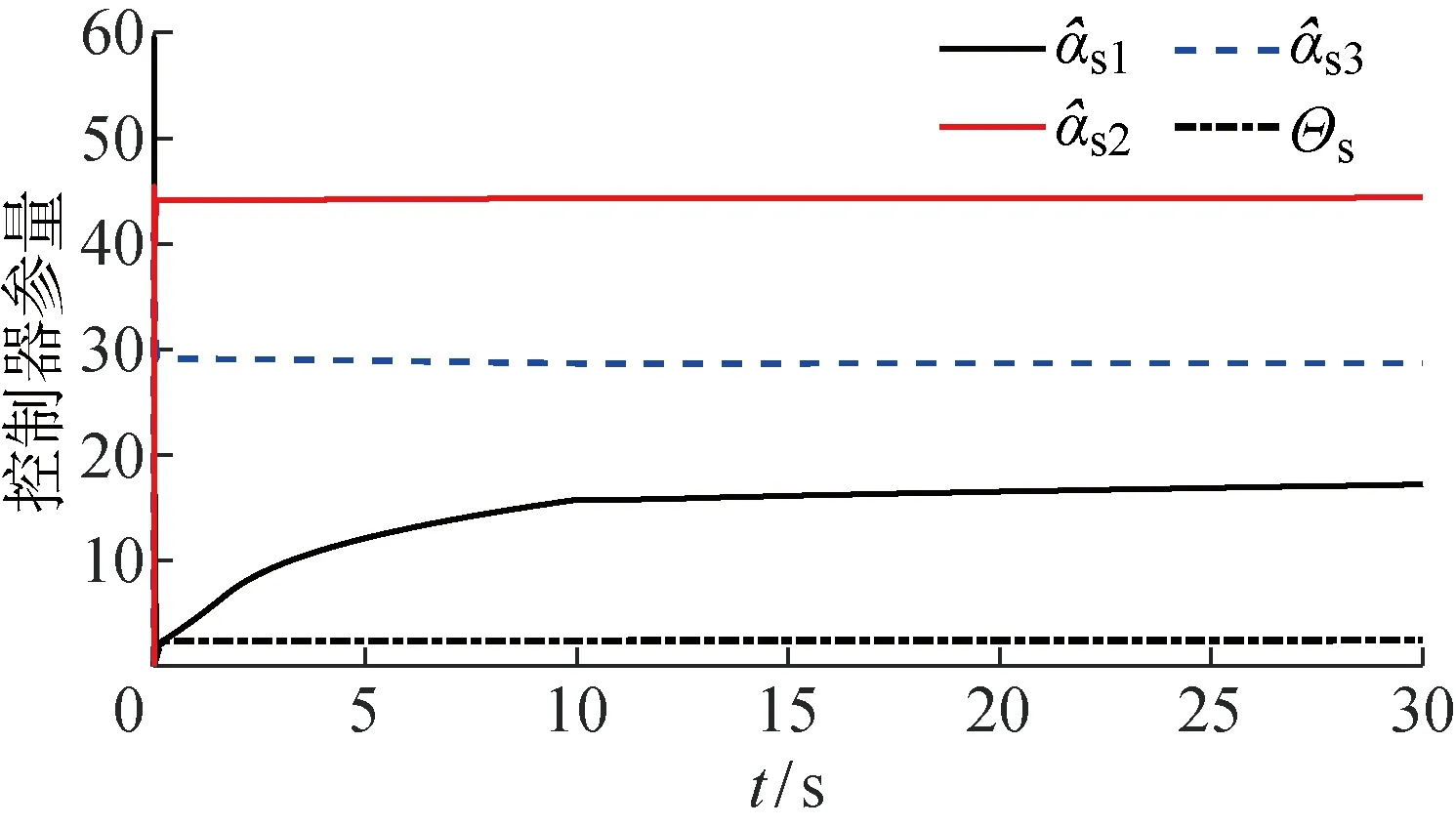
式中:xe为一维空间下,从机械手与接触环境的位置;ke为抓取目标的刚度系数.xs 图2 遥操作机械手结构示意图 设操作者只在操作空间x轴方向施加作用力,x轴方向刚度系数ke=100 N/m,y轴方向不施加作用力.从机械手在x轴方向xe=0.1 m处与抓取目标接触.仿真时间设为30 s,前10 s在主机械手上施加10 N的作用力,然后将作用力设为0 N.即在机械手上施加10 N作用力持续10 s,然后不再施加力,持续20 s,观察机械手的力-位移跟踪状态. 图3~5中f为作用力,qi1、qi2为qi的元素.从手、主手操作空间位置实现对主从机械手设定阻抗模型期望位置跟踪,同理实现从手对主手的关节位置跟踪,在主手上操作者施加力与从手和环境中之间交互力一致协调相等.从手初始位置位于与抓取目标不接触的自由位置,跟踪主机械手位置运动到0.1 m时实现于抓取目标交互,此时从手依然实现对主手的位置跟踪,此时主手上开始感受到从手的反馈力以致到主手力信号与从手力信号误差渐进收敛于0. 图3 遥操作机械手力跟踪曲线图 图4 主从机械手参考位置与位置跟踪曲线图 图5 遥操作主从手关节角度跟踪曲线图 图6 主手自适应律曲线图 图7 从手自适应律曲线图 在系统模型不确定以及外部干扰条件下,整体系统仍然保证从手对主手的力跟踪以及从手对主手的位置跟踪.主手内部不确定自适应律以及外部干扰上界不确定自适应律对外部干扰以及自身模型不定性的补偿,满足了鲁棒稳定性特征. 为了验证所设计控制器的先进性与优越性,所设计的控制器(新控制器)与文献[1]的模型参考自适应控制和文献[2]的PD+like控制器做了相应比对.针对式(1)所示包含关节摩擦及外部干扰的机械手模型,在主手x方向加10 N的力信号,3种控制器的力跟踪与位移跟踪曲线如图8和9所示. 由图8和9可知,所提出的控制方法跟踪过程具有快速性及无静态误差的特点,避免了由于外部干扰引起的震荡特点. 图8 不同控制器条件下主、从手力跟踪曲线图 图9 不同控制器条件下主、从手位置曲线图 提出了基于阻抗参考模型的自适应控制方法实现主手、从手力位移信号的同步.通过建立线性二阶微分方程的参考阻抗模型,将主从手参考阻抗模型的动态响应期望位置作为主从机械手末端的操作空间下的位置跟踪目标.对机械手动态参数不确定在线学习估计,对外界干扰作不确定上界估计,并且设计了滑模控制项消除内部干扰与外部不确定干扰,保证了主从机械手闭环动态方程与参考阻抗模型动态方程相一致,实现了主从机械手末端对参考阻抗模型输出的期望位置误差渐进收敛于0.利用李雅普诺函数证明了系统的稳定性及透明性,在MATLAB/Simulink上进行仿真实验验证了控制系统的鲁棒性及自适应能力.
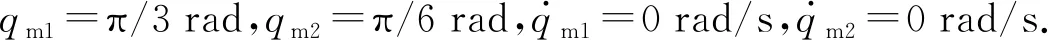
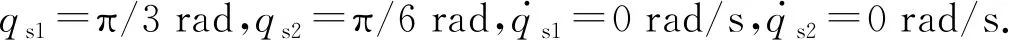






6 结语
