无线携能通信中基于时间反演的能量效率优化

陈善学， 刘祚粮， 李方伟

(重庆邮电大学 重庆移动通信工程研究中心， 重庆 400065)

近年来，随着能源革命的进行，人们的聚焦点不再局限于石油、热能等传统能源，而是依托于先进的科学技术探索出了风能、热能等新兴的可再生能源.存在于自然环境中的无线射频信号由于具有既能传输信号又能传输功率等优点，很快成为了新的研究热点[1-2].

无线携能通信(SWIPT)能够在信息解码的同时对设备进行无线充能，其概念最早由Varshney提出[3]，并在整个通信行业取得了较大发展.但已有的SWIPT文献大都是针对吞吐量最大化、总信息速率最大化以及频谱效率最大化的研究[4-6]，对能量效率(EE)最大化的研究很少，而随着数据业务量的增长和能耗的加大，未来的无线网络将会追求一个能效利用率更高的通信方式[7-8].在满足各自约束的条件下，文献[9-12]分别研究了广播信道、多址接入、中继网以及无线传感网等中的SWIPT最大化EE算法.这些优化算法虽然提高了系统的能量利用率，但是需要在特定的条件下对优化目标进行理论建模.时间反演(TR)是一种利用多径效应创造空时聚焦效果的信号处理技术，能够极大地增强接收端的信号强度，简化接收机结构[13-15].文献[16]中，研究者将TR引入SWIPT的窃听系统，提出一种新型的物理层安全传输方案，极大地改善了系统的传输安全性.因此，为了追求一种新的优化方向，可以考虑利用TR来提高系统的可实现信息速率和收集到的能量，然后再进行算法优化.

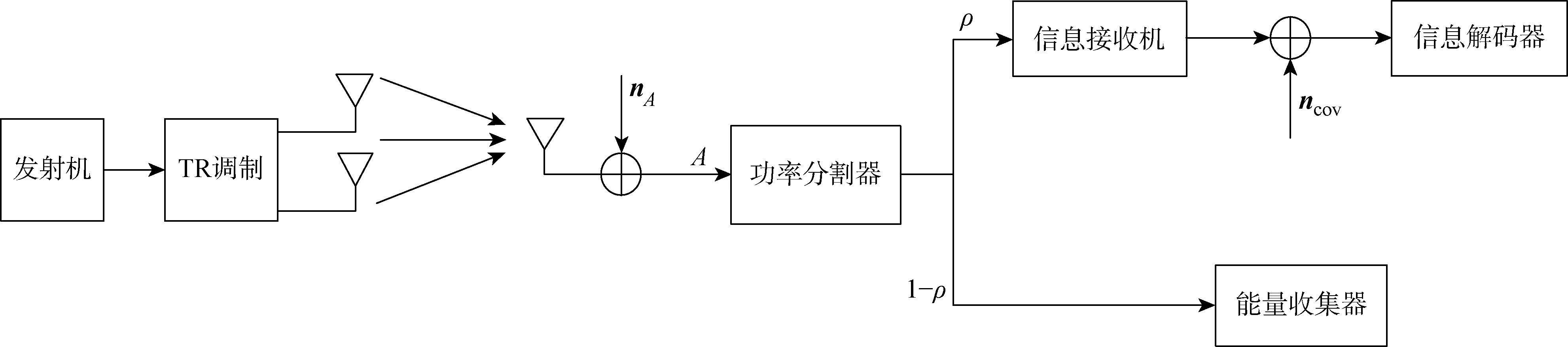
图1 TR-SWIPT系统模型

本文将TR引入SWIPT中，利用TR的时空聚焦特性来提高接收到的信号强度，并提出一个联合天线发射功率和功率分割比例的EE优化问题.该问题的目标函数是一个二维的非线性非凸规划问题，可以通过目标函数的变换转化为线性凸优化问题，然后用Dinkelbach的一维搜索算法和CVX求出最优解.在仿真部分，分别对天线数量、多径数量、搜索精度、最大发射功率以及整流噪声功率对能量效率的影响做了相关分析，并对传统SWIPT[1]、未优化的TR-SWIPT[16]以及优化后的TR-SWIPT三种传输方案的性能进行了对比.

1 系统模型

考虑点到点传输的TR-SWIPT系统，该系统只有1个发射端和1个接收端，其中，发射端配有M根发射天线，接收端配有1根天线.为了方便，功率分割器(PS)采用分离式结构以及动态功率分割方式，系统的信道状态信息在1次完整的通信过程中保持不变，即从信道探索阶段到信号再发射阶段不变.此外，完美的信道状态信息已经被系统获知.

系统模型如图1所示，在频率选择衰落信道上的TR-SWIPT通信过程可分为3步进行：

(1) TR调制器对发射机发送的符号进行调制后，用M根发射天线向目标接收机传输信号；

(2) 由于TR的时空聚焦特性，被发送的信号将在目标接收机处形成聚焦，然后被接收机接收；

分析上述通信过程，待发送的数据符号用s表示，满足均值E[|s|2]=1，则在A点接收到的信号yA∈C2L-1可以写作：

(1)

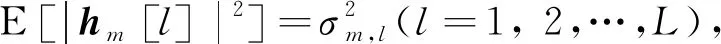
(2)

式中：hm[L+1-l]是hm[l]为复数时的反转共轭操作；gm[l]已进行归一化操作.

A点的信号功率为

(3)

式中：psig为理想信号功率，将功率的ρ部分传给ID，其余(1-ρ)部分传给EH，所得信号功率表达式分别为

(4)

pEH=(1-ρ)pA=

(5)

对于经过时间反演调制后传输的信号，由文献[17]可知，信号功率在传输过程中损耗较小，大部分功率都聚集在中心抽头，即第L个抽头，所以只需要在第L个抽头取1次值，就可以得到理想信号的功率.

2 问题规划和算法设计

2.1 问题规划

根据上节推导出的pID和pEH，可得到以P和ρ为自变量的信噪比(SNR)、可达信息速率(R)及收集到的能量(Q)，分别为

(6)

R(P,ρ)=

(7)

(8)

式中：B为功率转化；ζ表示能量的转化效率(不是本文关注的重点)，为了不失一般性，设ζ=0.8，即线性能量收集.需注意的是，以上性能指标都是指单位时间内数值.

再假设传输过程中的数模转换器、模数转换器、频率合成器等固定消耗的能量为PC(不包括天线的发射功率)，收集到的能量作为整个系统能量消耗的补偿，则整个系统实际消耗的能量可以表示为

Qt(P,ρ)=PC+P-Q(P,ρ)=

PC+P-ζ(1-ρ)

(9)

因此，系统的能量效率可以表示为

(10)

式(10)中，无论是增大R(P,ρ)，还是减少Qt(P,ρ)，都可以在一定程度上增大ηe.但是考虑到实际的原因，系统必须在满足一定大小R(P,ρ)和Qt(P,ρ)约束的前提下，才能通过变量P和ρ的调整来使ηe达到最大.针对上述情况，提出规划问题P1：

(11)

s.t.R(ρ,P)≥Rmin

(12)

Q(ρ,P)≥Qmin

(13)

0≤P≤Pmax

(14)

0≤ρ≤1

(15)

式中：Rmin为系统的最小可达信息速率，以保证系统的通信服务质量；Qmin为最小收集到的能量，以维持设备的正常工作时长；Pmax为天线的最大发射功率.

2.2 算法设计

对问题P1进行数学分析，发现目标函数是R(ρ,P)和Qt(P,ρ)的比，所以P1是1个二维的分式非线性规划问题，并由目标函数的Hessian矩阵可知，P1还是1个非凸问题[18].

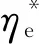
(16)

当F(ηe)=0时，R(ρ,P)和Qt(P,ρ)取得最优值ρ*和P*，此时式(16)的最优解就是问题P1的最优解，在定理1中进行了证明.

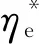
证明：因为

0≤ρ≤1， 0≤P≤Pmax

且

即

所以ρ*和P*是问题P1的最优解，证明完毕.

通过上述分析可以将问题P1转化为问题P2：

(17)

s.t.R(ρ,P)≥Rmin

(18)

Q(ρ,P)≥Qmin

(19)

0≤P≤Pmax

(20)

0≤ρ≤1

(21)

继续对问题P2进行分析，发现目标函数，即式(17)对P偏导的Hessian矩阵不大于0，即

(22)

这说明，对于在[0,1]内任意取值的ρ，目标函数都是凹函数.同理可知，式(18)是凹约束.此外,式(19)～(20)均为线性不等式，则P2为1个一维的线性凹规划问题，可以用任意凸优化方法得出最优解.

考虑一维搜索，在给定功率分割比ρ1∈[0,1]的条件下，问题P2的Lagrange函数为

L(P,α,β,λ)=(1+α)R(ρ1,P)-

ηeQt(ρ1,P)-αRmin+

βQ(ρ1,P)-βQmin+λ(P-Pmax)

(23)

式中：α、β及λ为Lagrange乘子.又根据一阶库恩塔克条件，令

可以求得P的解如下,然后再对ρ进行搜索.

(24)

为了仿真方便，本文采用CVX对问题P2进行求解，构建对于EE的优化算法.CVX是一种用于构造和求解凸优化的建模系统，能够使用标准的MATLAB语法表达具体的约束函数和目标函数，从而快速构建包含凸优化的算法原型，并进行相应的求解.算法如下：

(1) 将一个任意小的正数δ作为算法的结束门限.

(3) Loopρ=0∶k∶1

If 问题P2可行，则

(a) 用CVX求得最优值(G*,ρ*,p*).

(b) 将最优值(G*,ρ*,p*)加入矩阵S的第n行中.

Else

继续循环.

End if

End loop

(4) 从矩阵S第1列中选择G值最大的1行 [G(n)ρ(n)p(n)].

(5) IfR(ρn,Pn)-ηeQt(ρn,Pn)>δ(δ为暂停算法的阈值)，则

(b)n=n+1,矩阵S重新设为0矩阵.

(c) 返回步骤(3).

Else

(a) 问题解决.

(b) 结束算法.

End if

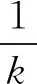
(25)

3 数值仿真和分析

本节对提出的优化算法进行仿真和分析，研究搜索精度、最大发射功率、整流噪声功率及信噪比变化对能量效率造成的影响，并对不同的SWIPT传输方案进行性能对比.仿真参数设置见表1.此外，由于本节仿真的横轴和竖轴都是信噪比和能量效率，所以只在图中2分析信噪比变化对系统能量效率造成的影响.

图2为Rmin=100 kb/s，Pmax=30 dBm，Pcov=-10 dBm时，能量效率随着发射精度和信噪比增大的变化趋势.从图中可以看到，信噪比随着能量效率的增大而增大.由于系统的可达信息速率增大时，实际消耗的能量减少，所以R(ρ,P)与Qt(ρ,P)的比值增大，能量效率增加.此外，信噪比较小时，搜索精度对能量效率的影响较小；而当信噪比大于一定值时，PS端信号功率变大，搜索精度的增大会提高能量效率.这是因为最优解可能隐藏在那些未被取到的ρ值上，所以当搜索的ρ值越全面时，最后得到的解的值就可能越大.

表1 仿真参数

图2 信噪比、搜索精度变化对能量效率的影响

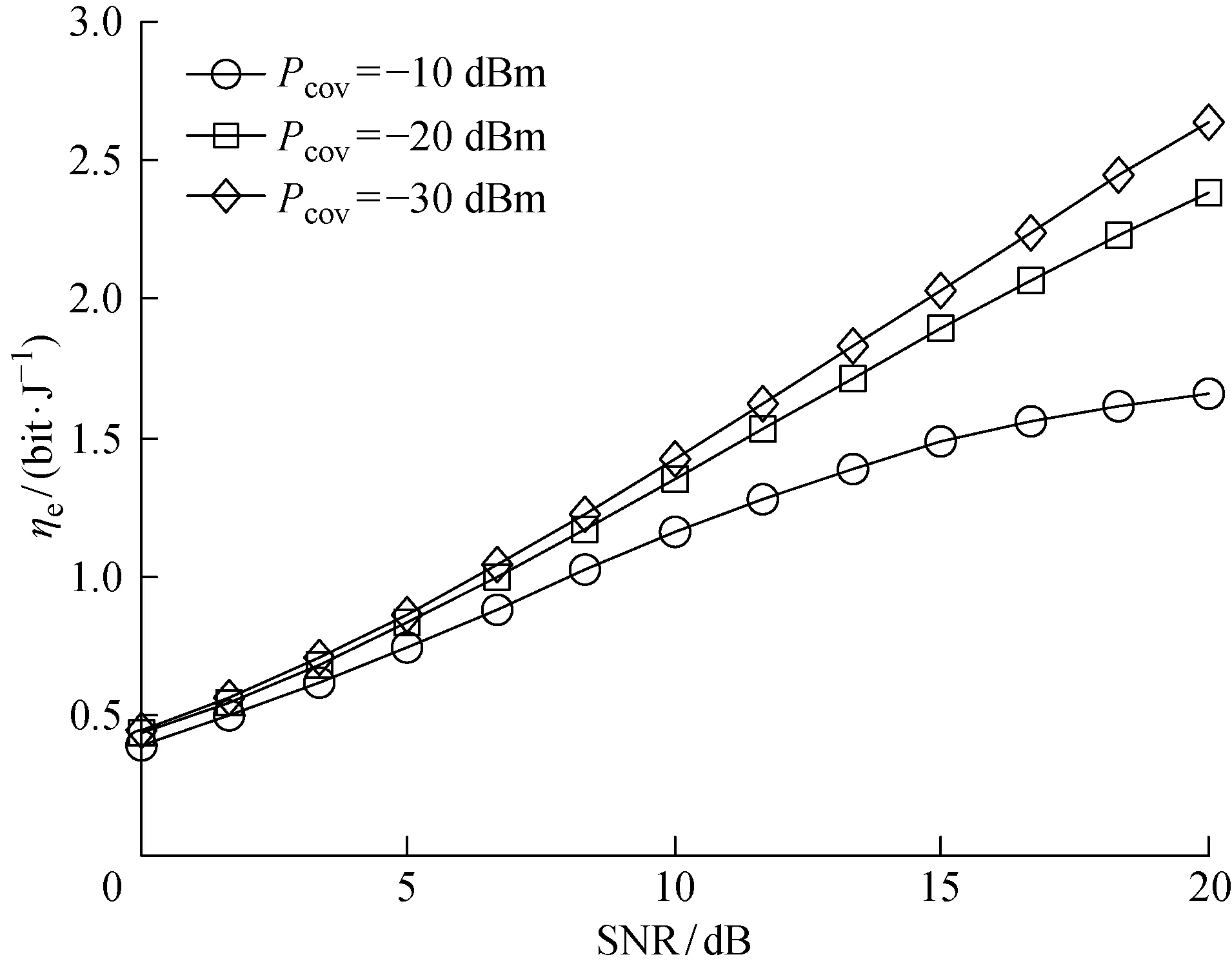
图3 解码噪声变化对能量效率的影响

图3为k=0.10，Rmin=100 kb/s，Pmax=30 dBm时，能量效率随解码噪声和信噪比变化而变化的趋势.从图中可以看到，解码噪声功率为 -10 dBm时，系统的能量效率在整个信噪比的变化区间内均为最小；而解码噪声功率为 -30 dBm时，能量效率的值处最大.由于解码噪声功率主要影响可达信息速率的大小而不影响系统的实际能量消耗.所以，随着解码噪声功率的增大，系统的能量效率开始降低.而当解码噪声功率减小时，可达信息速率变大，R(ρ,P)与Qt(ρ,P)的比值变小.

图4为k=0.10，Rmin=100 kb/s，Pcov=-10 dBm时，能量效率随最大发射功率和信噪比变化而变化的趋势.从图中可以看到，Pmax=10 W时的能量效率最大，Pmax=1 W时得到的能量效率最小，而Pmax=5 W时，能量效率则处在最大和最小中间.这说明，在满足给定约束的条件下，随着最大发射功率的增大，系统的能量效率也逐渐增加.由于最大发射功率对可达信息速率的影响大，对实际消耗能量的影响小，所以影响了R(ρ,P)与Qt(ρ,P)的比值.

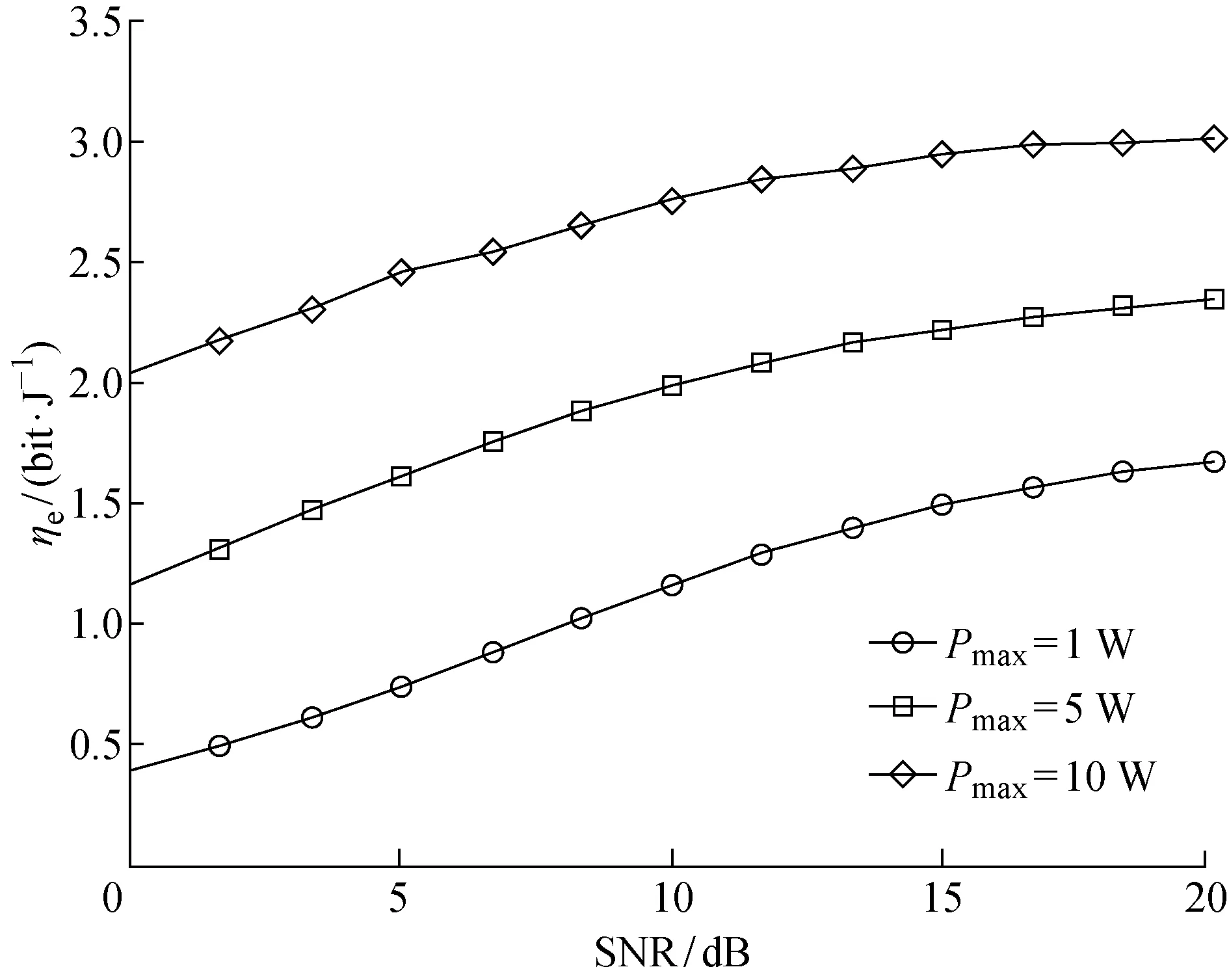
图4 最大发射功率变化对能量效率的影响

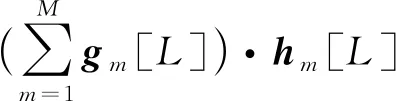
图5 天线数量和多径数量对能量效率的影响

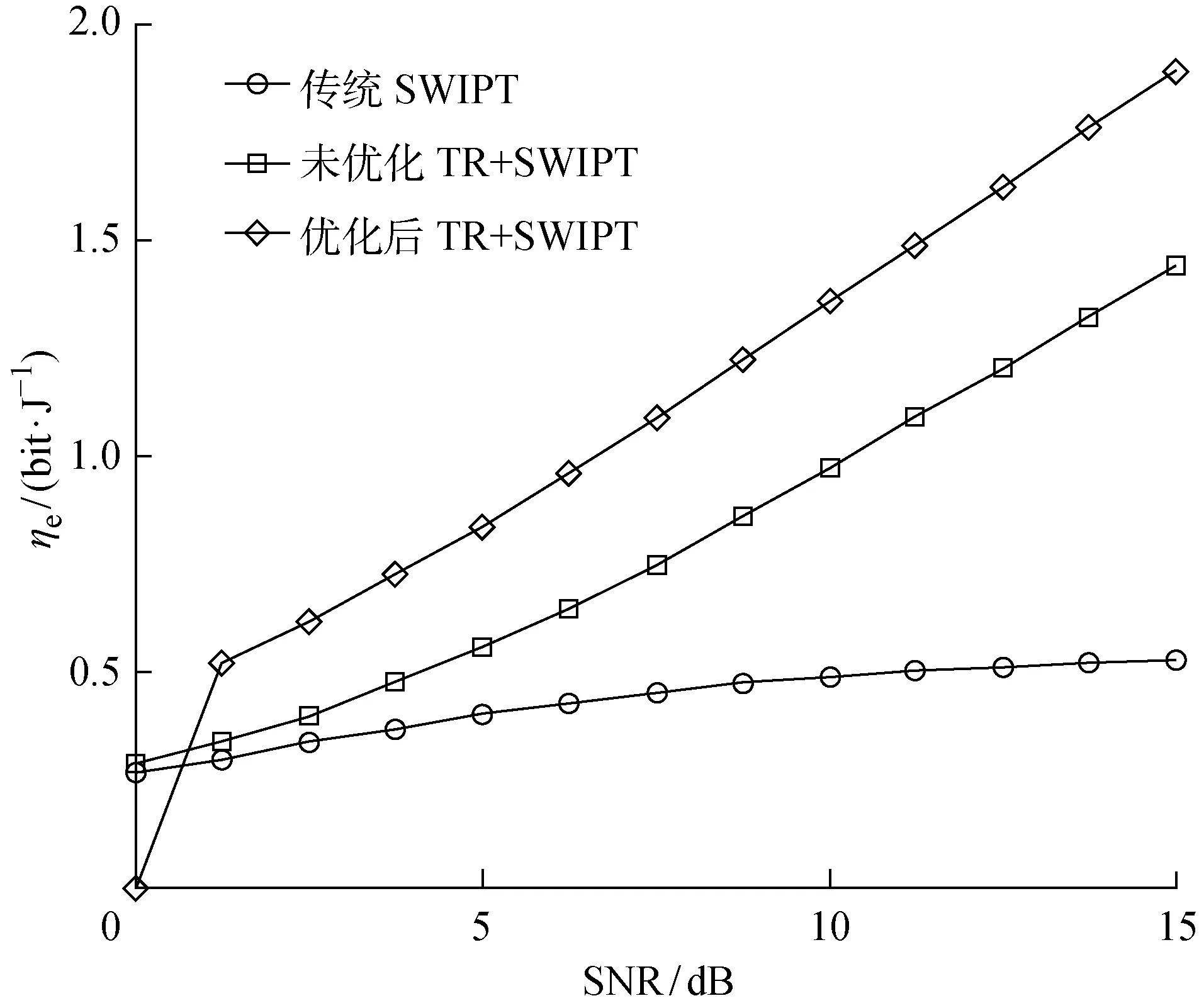
图6 不同传输方案的能量效率对比

图6为k=0.10，Rmin=120 kb/s，Pmax=30 dBm，Pcov=-20 dBm时，分别对传统SWIPT[1]、未优化的TR-SWIPT[16]及优化后的TR-SWIPT 3种传输方案进行的性能对比.可以看出，信噪比为0时，即理想信号功率等于噪声功率时，问题P2不可行(不满足约束条件)，则能量效率为0.在3种传输方案中，当优化后的TR-SWIPT满足P2约束条件时，系统得到的能量效率大于其他两种传输方案得到的能量效率，且其他两种传输方案没有约束条件.值得注意的是，无论信噪比变化如何，相较于SWIPT，未优化的TR-SWIPT 的能量效率均较大，说明TR具有良好的优化性能.

4 结论

对SWIPT进行能量效率优化，将TR加入SWIPT的能量效率优化中，考虑点到点传输的TR-SWIPT新型传输优化问题，并推导了能量效率的闭合表达式.主要结论为：

(1) 当信噪比、最大发射功率、天线数量及多径数量增加时，能量效率增大；

(2) 信噪比较小时，搜索精度对能量效率的影响较小，而当信噪比较大时，搜索精度越大，能量效率越大；

(3) TR能够改善SWIPT的能量效率，而本文提出的基于时间反演的优化算法提升的性能更大.