一种NoisyRounds 保护的白盒AES 实现及其差分故障分析*

孙 涛, 唐国俊, 吴昕锴, 毛振宁, 龚 征

华南师范大学计算机学院, 广州510631

1 研究背景

在移动互联网与物联网终端及其软硬件技术交替演进当中, 可信计算、身份认证、密码算法等网络与信息安全关键要素已得到充分重视. 绝大多数产品在理论上遵照密码学广泛采用的Kerckhoffs 原则(即一个密码系统的安全性仅依赖于密钥的安全性). 因此工业界也陆续制定了TPM、Trustzone、SGX、TEE、SE 等一系列技术用于保护密钥存储与运算中的完整性与机密性. 在保护密钥安全的基础上, 通过各种标准密码算法或安全协议对数据、身份和隐私信息进行安全加固. 在实际中, 由于移动互联网、物联网硬件资源往往受到限制, 在软件上又需要考虑设备兼容性等问题, 采取基于硬件安全(TEE、SE) 保护密钥的应用解决方案在总体上还仅占很小比例, 绝大多数应用仍然通过传统软件加固的方式(代码混淆、程序加壳、内存防dump) 来保护应用安全方案中的密钥. 但相关软件加固技术往往依赖于厂家自身的设计与分析, 缺乏理论安全性验证. 在CCS 2018 会议上, 李卷儒等人通过分析密码算法与密钥在二进制代码存储与运算中的特征, 设计并实现了一种通用的二进制代码密钥恢复工具(K-HUNT)[1]. 针对OpenSSL、mbedTLS 等著名开源密码算法库及一些私有密码算法相关软件的实验结果表明K-HUNT 均能对二进制代码中的密钥进行恢复攻击. 上述攻击案例表明传统软件加固方式作为密钥保护技术还远远不够, 攻击者往往能通过静态代码逆向分析、动态程序跟踪等方式直接获取密钥. 在物联网、移动互联网等资源受限应用场景下, 由于分组密码算法(block cipher) 在性能与效率上的优势, 因此在数据加解密、消息认证码与数字版权管理方案的构造中往往起着重要作用. 在此背景下, 越来越多的厂商在应用中引入了白盒分组密码算法(white-box block cipher) 来构建软件环境下的密钥安全保护机制, 由此也进一步提高了学术界与工业界对白盒分组密码算法的研究与关注度.

白盒密码学(white-box cryptography) 由Chow 等人[2]在SAC 2002 年会上首次提出, 其核心思想是通过白盒密码实现技术, 使得密码算法的软件实现与运行环境在对攻击者完全开放的前提下, 密码算法所使用的用户密钥仍然不能被攻击者所获取. 在提出白盒密码学概念的同时, Chow 等人也针对国际分组密码算法标准AES 和DES 给出了相应的白盒实现方案[2,3]. 由于白盒分组密码算法仅依赖于软件实现,具有良好的兼容性和可维护性, 目前已得到了密码学界和工业界的广泛研究与关注. 在防火墙、无人机、APP 等应用中, 白盒分组密码算法已作为软件完整性保护、身份认证、密钥管理与分发等功能的关键信息安全保护技术加以实际应用.

在Chow 等人提出基于查找表的AES 标准分组加密算法的白盒实现后[2], 从矩阵、仿射变换分析入手进行白盒方案破解的工作也伴随而来. Billet 等人于2004 年提出了基于矩阵求逆方法的白盒密钥恢复攻击技术(简称BGE 攻击)[4], 该技术能以232左右的计算复杂度对Chow 等人所提出的AES 白盒实现及其类似构造的白盒分组密码算法进行密钥恢复. 针对Chow 等人提出的DES 白盒实现, Wyseur 等人也提出了类似破解方法[5]. 在BGE 攻击方法提出后, 陆续也有新的白盒AES 实现方案提出, 在此基础上, 针对Chow 类型的白盒AES 实现的分析方法也不断改进. Bringer 等人在2006 年提出了一种白盒AES 实现方案[6], 但在2010 年De Mulder 等人给出了相应的攻击方法[7]. 2009 年肖雅莹和来学嘉提出了一种改进内部编码方式的AES 白盒实现方案[8], 该实现在2012 年被De Mulder 等人以232的计算复杂度破解[9]. 在2010 年, Karroumi 基于dual cipher 的思想提出了一种新的白盒AES 实现方案[10], 但2013 年Lepoint 和Rivain 提出的新分析方法, 将攻击Chow 等人和Karroumi 提出的白盒AES 方案及其类似变种的计算复杂度均降低至222[11]. 2016 年Baek 等人提出内部状态(internal state) 的大小决定了白盒实现的安全强度, 并基于此理念, 通过编码连接两个AES 实例的方式提高内部状态的大小, 给出了一个新的白盒AES 实现方案[12]. 在Eurocrypt 2018 上, Dinur 通过改进的仿射变换等价变换方法, 将m 比特S 盒的仿射查找表变换的最优攻击复杂度提高到O(m32m)[13]. 随后在CHES 2018 上, Derbez等人[14]指出Dinur 算法[13]的不足之处, 给出了针对SPN 结构+ 仿射变换的白盒分组密码算法的高效通用分析方法. 针对Baek 等人提出的白盒AES 实现方案[11], Derbez 等人在该高效通用分析方法的基础上给出了计算复杂度为231的破解方案[14]. 在上述分析方法的影响下, CHES 2016/2017 连续两年举办的AES 白盒实现竞赛均无方案能抵抗密钥恢复攻击[15].

在理论上, 白盒安全模型在算法运行状态下对攻击者并无秘密可言, 但在实际中, 存在一类研究方向, 即对白盒算法设计与实现提出秘密组件(secret components) 的前提条件, 其中具有代表性的就是Biryukov 等人提出的ASASA 框架[16]. 该类工作往往假设分组加密算法的S 盒或扩散层采用了秘密参数加以实现, 该秘密参数对攻击者并不公开. 由于该秘密参数的存在, 使得白盒模型下的攻击者进行密钥恢复攻击的难度大大增加. Chow 等人所提出的白盒分组密码实现中, 外部编码(external encoding) 由于也是对攻击者保密, 因此也可以看作是算法白盒实现的秘密组件. 针对上述设计方案, Bos 等人提出了基于差分计算分析(differential computation analysis, 以下简称DCA) 和差分故障分析(differential fault analysis, 以下简称DFA) 的侧信道分析方法[17], 能将设计方案中的隐藏S 盒或其他组件加以恢复, 从而最终实现白盒算法的密钥恢复攻击. 上述侧信道分析方法一经提出, 在AES 白盒实现的破解上也取得了很好的实际破解效果. 在分析CHES 2017 AES 白盒实现竞赛中各种参赛方案的基础上, Goubin 等人归纳出linear decoding analysis (LDA) 方法, 该方法能有效解决代码混淆后的白盒分组密码的秘密组件分析问题[18]. Lee 等人提出在轮函数线性变换到非线性变换之间增加随机掩码的方式, 能有效提升白盒实现抵抗DCA 攻击的安全性[19]. 在2019 年Journal of Cryptology 上, Bock 等人在Bos 等人DCA 和DFA 工作的基础上, 提出了dynamic binary instrumentation (DBI) 安全框架用于白盒模型下密码算法的侧信道分析[20]. 在SAC 2019 上, Amadori 等人通过结合BGE 攻击技术, 使得DFA 攻击能对增加了8 比特输出外部编码的白盒AES 方案进行攻击, 该方法的密钥恢复攻击复杂度为O(232)[21].

由于在资源受限环境下, 在分组密码算法设计上增加侧信道保护还需要考虑其实现代价. Zhou 等人的探索性工作表明, 轻量级分组密码算法也可以采用查找表或仿射变换的形式进行白盒实现[22]. Xu 等人提出增加轮函数冗余和查找表变换的方式来模糊轮函数边界, 进而达到增大AES、SM4 等基于S 盒-线性扩散类型分组密码白盒实现的分析难度[23]. 如何在实现分组密码算法白盒安全性的基础上, 能够抵御各种侧信道分析方式对算法实现秘密参数或组件的恢复攻击, 并不是简单的技术叠加. 同时, 算法增加侧信道保护技术后能否与白盒实现有机整合, 尽可能地降低白盒实现的性能与资源开销, 这也是决定白盒分组密码算法能否具有实用性的关键问题之一.

在LATINCRYPT 2012 年会上, Gierlichs 等人提出了DummyRounds 技术[24]. 该技术通过巧妙利用分组密码轮函数存在不动点的特性, 通过增加随机等效轮的方式来实现密码算法硬件实现的抗故障攻击. 在CRYPTO 2016 年会上, Schneider 等人提出将奇偶校验码(parity code) 和门限化实现(threshold implementation) 的ParTI 方案, 并针对PRESENT 分组密码算法实现了抗差分能量攻击和故障攻击的一体化保护[25]. 虽然DummyRounds 技术和ParTI 方案均有效地抵抗了故障注入攻击, 但DummyRounds 技术要求算法密钥不能预先固定, 这与白盒分组密码算法的密钥由白盒密钥表预计算完成并分配的实用方式不符. 同时DummyRounds 技术和ParTI 方案仅适用于硬件实现下的侧信道防护,如果在白盒实现中直接采用上述技术, 攻击者可以简单的旁路掉DummyRounds 或ParTI 方法中的保护测试部分, 使得故障注入还是能取得预期效果. 与DummyRounds 技术类似的是, 韩国KAIST 的学者Lee 和Kim 也提出了基于Table Redundancy 的方式来抵抗DFA 分析[26]. Table redundancy 方法主要原理是通过并行MixColumns 步骤, 将计算结果进行对比, 如果白盒实现遭受到DFA 攻击, 那么并行MixColumns 步骤会导致输出结果无法用于进一步的DFA 分析.

在上述工作的基础上, 本文针对一类添加了内/外部掩码的随机冗余轮函数保护的白盒AES[15](由于此类保护方式与DummyRounds 具有相似性, 我们将该方法命名为NoisyRounds), 给出了在各种内、外部编码与冗余轮函数条件下的DFA 分析. 从我们基于Deadpool 工具[27]改进后的自动化DFA 分析结果来看, 如果仅仅在AES 轮函数中增加n 轮DummyRounds, 那么DFA 攻击者只需线性增大获取错误密文数量即可成功恢复密钥. 在添加n 组NoisyRounds 保护后, 密钥恢复难度为NoisyRounds 组数n的(n+1)4计算复杂度. 在带外部编码的情况下, NoisyRounds 与现有保护方案一样能抵抗DFA 工具的分析. 虽然外部编码能够抵抗DFA 分析, 但算法加解密结果也将带上相应的编码, 与标准加解密结果不能一致, 将失去在不同系统间的兼容性. 因此实际白盒AES 应用中，如何在不添加外部编码的前提下抵抗DFA 攻击也非常重要. 上述分析结果对于研究灰盒模型下常用的随机冗余轮技术在白盒模型下的安全性具有参考意义.

2 背景知识

2.1 Chow 等人的白盒AES 实现

分组密码算法AES-128 共10 轮[28],轮函数包括SubBytes、ShiftRows、MixColumns 和AddRound-Key 四个组成部分. 首轮之前, 先做一次AddRoundKey, 末轮没有MixColumns. Chow 等人针对AES-128 设计的白盒密码方案[2](以下简称: Chow-WBAES) 的思路是调整加密顺序, 改变算法每一轮的边界,构成轮函数加密依次如下顺序: ShiftRows, AddRoundKey, SubBytes 和MixColumns 的轮结构, 如再将AddRoundKey 与SubBytes 组合成查表操作, 即建立8 比特输入到8 比特输出的查找表, 称为T-box,从而将密钥隐藏在查找表中. 需要指出的是, 由于AES 的轮状态可用4×4 单元表示, 除ShiftRows 以外, 其余操作均在当列操作, 所以在AES 的白盒实现中可以列单位进行白盒查找表的建立与加密运算. 本文在部分描述中, 将以第1 列为例介绍Chow-WBAES.

对于一个字节的输入x , T-box 如下表示:

其中i = 0,··· ,15,r = 1,··· ,9, kr为第r 轮轮密钥, k0为第一轮之前的AddRoundKey 密钥. ˆkr[i] 表示kr经过ShiftRows 变换后的第i 个字节, i=0,1,··· ,15,r =0,1,··· ,10.

因MixColumns 每次作用在一列, 可由32×32 的矩阵MC 乘32 比特的列向量表示, 在白盒实现中加密时的MixColumns 与解密时的MixColumns 逆操作都可通过四个较小规模的8 比特输入到32 比特输出的查找表操作后再通过异或的方式完成. 加密时的查找表称为Tyi, 解密时的查找表称为invTyi,i=0,1,2,3. 构造如下表示:

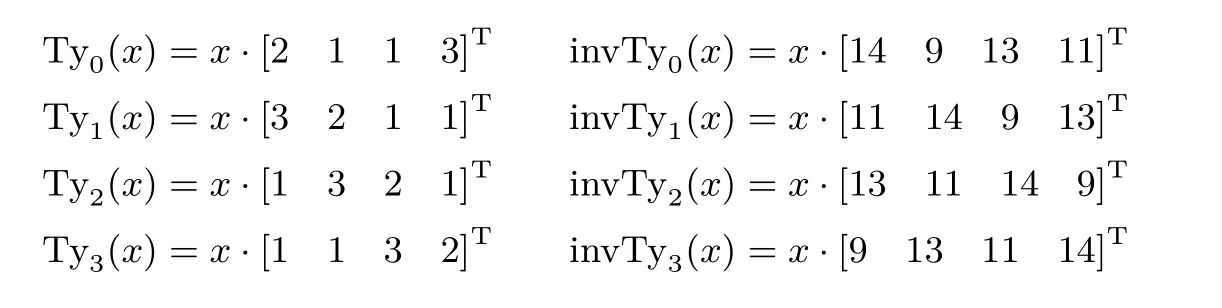
32 比特的列向量(x0,x1,x2,x3) 进行MixColumns 或MixColumns 逆操作可表示为4 次查表和3 次异或:

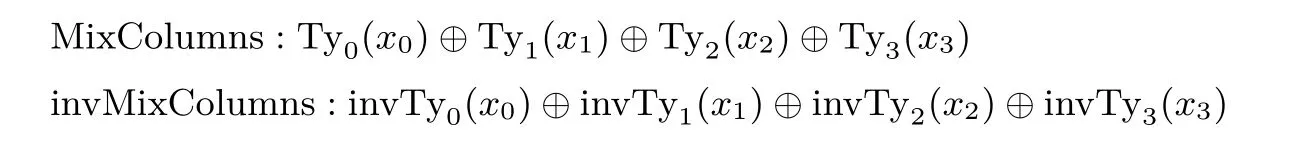
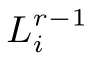
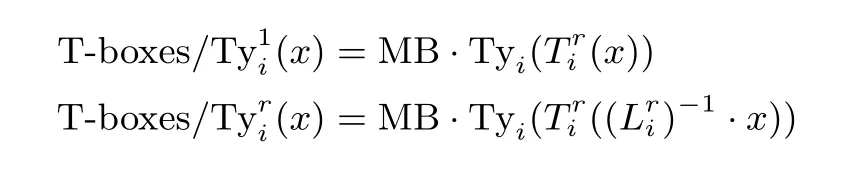
其中, i=0,··· ,3, r =2,··· ,9. 因此需要额外的查找表操作来抵消MB 的影响以及添加r+1 轮的输入置换, 所以构造8 比特输入到32 比特输出的查找表BijBox. 对于一个字节的输入x, 第1 列的BijBox有如下表示:

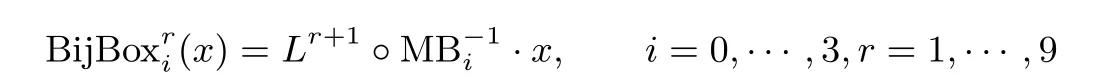
结合查找表, 原AES-128 算法加密操作便可转换为查表操作, 对于128 比特的明文plaintext, 其AES-128 加密有如下表示:

考虑到code lifting 攻击, 需要对白盒解密程序的输入密文和输出明文做编码来改变加密算法的明文与密文的映射关系, 防止攻击者在不还原密钥的情况下直接通过白盒解密装置解密密文, 得到原始的明文,而对加解密程序的输入输出添加的编码称为外部编码(external encodings). 用Dk表示AES-128 解密,F 表示外部输入编码, G 表示外部输出编码, 增加外部编码的解密程序如下表示:

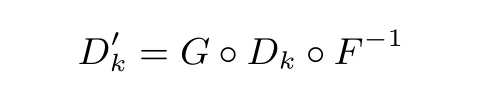
外部编码实现目前主要有线性和非线性编码, Chow 等人建议的是选择128 比特到128 比特的置换编码,并且将该置换转换成16 个8 比特到128 比特的查找表结合异或实现, 即在首轮之前, 添加额外的16 个8比特到128 比特的查找表和对应的480 个异或表来实现, 同样的在第10 轮之后, 也需要额外的查找表和异或表来实现G (也可与第10 轮的T-boxes 结合, 构成新的8 比特到128 比特的查找表). 再通过查异或表的形式合并. 如图1 的Type I 所示. 而在Muir[29]等人提出一种非线性编码方式, 使用16 个随机的8 比特的级联编码组成128 比特的非线性编码, 其构成如下:

这种编码方式可无需额外的查找表, F−1与第1 轮的T-box 输入结合, G 与最后一轮T-box 输出结合.

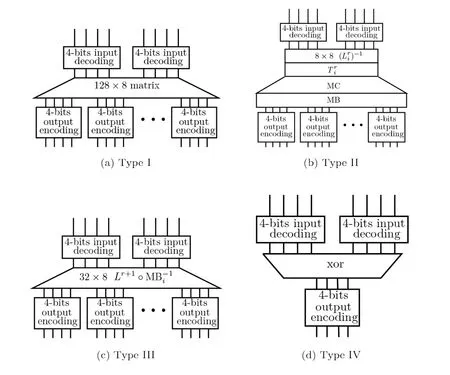
图1 Chow-WBAES 的四类查找表Figure 1 Four types of lookup tables of Chow-WBAES

2.2 针对Chow-WBAES 的差分故障分析

在本小节, 我们首先简要概述AES 差分故障攻击方法, 随后对Chow-WBAES 的差分故障攻击的基本原理与方法进行说明.

2.2.1 差分故障分析

在1997 年Crypto 会议上,Biham 和Shamir 提出了差分故障分析(differential fault analysis,DFA)这一概念, 并将其用于攻击DES 算法[30]. DFA 攻击的核心思想是通过对分组密码算法运行过程的中间值注入错误, 从而诱导出错误密文并加以收集, 将错误密文与正确的密文进行分析, 最终恢复出相应的轮密钥. 由于分组密码算法的密钥扩展函数大多具有可逆性, 因此在通过DFA 攻击方式获取分组密码算法的轮密钥后, 可以根据对应算法的密钥扩展函数逆推出相应的主密钥. 例如在AES-128 中, 攻击者获取最后一轮的轮密钥即可恢复主密钥, AES-192 和AES-256 则需要最后两轮的轮密钥才能恢复主密钥.

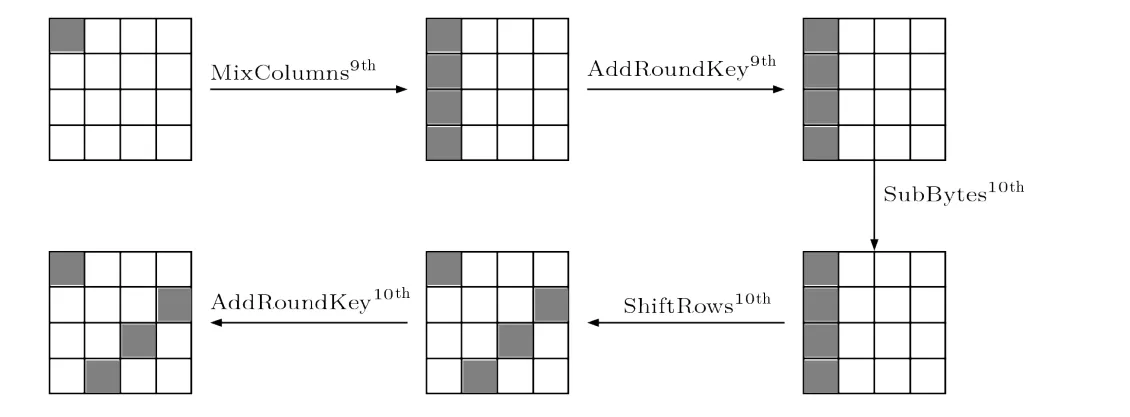
图2 Dusart 等人对第九轮AES 的差分故障攻击示意图Figure 2 Illustration of Dusart et al.’s DFA from 9th round AES

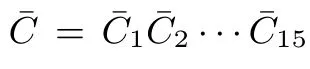
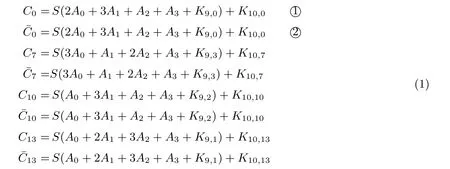
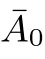
将公式(2)中的3○4○式相加可得:

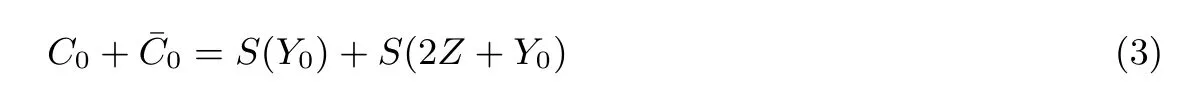
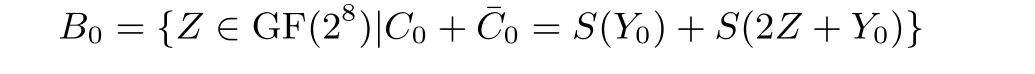
2.2.2 对Chow 等人的白盒AES 实现的差分错误分析实例

本小节将介绍针对Chow-WBAES 的DFA 攻击实例. 一般情况下, 攻击者在对白盒实现实施差分故障攻击时, 首先运行正常的加密程序得到正确的密文并记录, 然后在加密程序的二进制流或白盒查找表中注入错误, 最终筛选合适的错误密文用于计算可能的轮密钥候选值. 在Bos 等人开创性的白盒分组密码DFA 攻击方法[17]后, 陆续有基于DFA 自动化分析工具[27]破解白盒AES 的实际案例[32]. 此外,Teuwen 等人[33]也提出了使用Deadpool[27]工具成功分析Karroumi[10]和SECCON 2016[34]中的白盒AES 实现方案. 2019 年Bock 等人[20]详细提出了若干种能在软件环境下对密码算法进行注入错误的方法, 有以下5 种:

(1) 通过code lifting 将白盒加密程序转换成高级语言(例如C/C++), 这样就可以将注入错误的代码插入到白盒加密的过程当中.

(2) 将白盒程序运行在二进制动态插桩分析(dynamic binary instrumentation, DBI) 的框架下(例如intel PIN[35]或Valgrind[36]) 并插入诱导错误的代码.

(3) 使用支持脚本的程序调试器(例如gdb) 对白盒程序进行调试, 通过脚本自动化地去对注入错误以及收集对应的密文.

(4) 将程序运行在Unicorn Engine[37]或PANDA[38]等模拟器当中, 则可以随时改变数据的值或插入代码, 从而达到对密码程序注入错误的目的.

(5) 在某些特定的情况下(例如白盒查找表或程序缺乏完整性检测机制) 向白盒查找表或程序注入错误, 使其输出错误的密文并对错误密文进行筛选.

当加密或解密程序进行安全加固后, 前4 种方法将难以实现, 本文所使用的分析工具Deadpool[27]采用了上述的方法(5) 的策略, 将错误注入到白盒程序中. Teuwen 和Hubain 中对Deadpool 的工作原理进行了阐述[33], 首先提出了两个基本的要求:

(1) 白盒加密程序所产生的密文不应该带有外部输出编码(external encoding), 因为使用外部输出编码时攻击者无法直接地分析出注入错误对密文的影响.

(2) 加密程序能多次运行, 确保能获得多对错误密文.接下来对Deadpool 平台的DFA 攻击进行描述:

(1) Deadpool 首先导入白盒查找表T 并运行加密程序E 得到正确密文C 并记录.

(2) Deadpool 尝试遍历T(使用优化算法降低遍历空间) 和并产生随机错误注入到T (通过对二进制中的某段地址异或一串随机值), 得到错误密文, 对比错误密文与正确密文, 符合要求的错误密文将被分类记录, 按列分为4 类.

(3) 遍历完成后,运用第2.2.1 节的方法,针对获取到的错误密文分别破解第10 轮轮密钥K10,0,K10,7,K10,10,K10,13.

(4) 根据K10逆推回主密钥.

Deadpool 系列攻击工具的开源, 引起了白盒密码界的广泛关注, 其对目前多个公开发表的白盒实现进行了DFA 攻击, 表1 展示了部分白盒AES 实现在DFA 攻击下的实际抵抗效果.

表1 部分白盒AES 实现在DFA 攻击下的实际抵抗效果Table 1 Actual status of partial AES white-box implementations against DFA attack

3 一种NoisyRounds 保护的AES 白盒实现

在本节中, 我们将提出一种可有效抵抗DFA 攻击的AES 白盒实现方案NoisyRounds-WBAES. 首先介绍NoisyRounds-WBAES 的原理及其实现, 然后通过Deadpool 平台的DFA 分析工具[27]的攻击实验, 我们给出在NoisyRounds 保护下的白盒AES 实现抵抗DFA 攻击的有效性.

3.1 NoisyRounds-WBAES 原理说明与分析

虽然Tao Xu 等人的轮边界混淆工作[23]被Yeom 等人采用积分攻击和BGE 攻击相结合的方式破解[39], 但特定结构的随机冗余轮函数(DummyRounds) 是否能抵抗侧信道攻击, 特别是DFA 攻击仍然有待详细研究. 因此本文基于Chow-WBAES 方案, 提出了一种针对白盒AES 实现的NoisyRounds 保护方案, 该方案结合了在灰盒模型中证明有效的DummyRounds 技术, 同时根据DFA 攻击的特点来设计冗余轮函数的结构. 以下将该方案简称为NoisyRounds-WBAES.

在CHES 2016 上, Bos 等人[17]提出了针对AES 白盒应用DFA 攻击的方案, 该方案选择AES白盒实现的最后两轮进行攻击, 该方案主要有以下两个特点: (1) 无需知道注入故障的具体值; (2) 无需跟踪寄存器和内存信息, 错误密文可直接输出. 该方案将单个字节的错误注入到MixColumns8th与MixColumns9th之间, 经过MixColumns9th以及第10 轮运算后, 最终得到与正确密文相比存在4 个错误字节的错误密文(该4 个错误字节分布符合ShiftRows 规律). 我们将MixColumns9th及第10 轮整轮称为“DFA 分析轮组”. 本文在Chow-WBAES 的基础上, 通过在实际的第10 轮后添加与DFA 分析轮组的结构一致的轮组来混淆DFA 攻击, 这样的轮组称为“NoisyRounds”, 而相对应的, 需要增加能够抵消新增的NoisyRounds 的轮结构已保证白盒实现的正确性. 在应用上述Deadpool 平台的DFA 分析工具攻击NoisyRounds-WBAES 时, NoisyRounds 与DFA 分析轮组都有可能被注入错误并输出错误密文,并且根据密文无法区分其来自二者中的哪一个. 又因为NoisyRounds 的查找表T-box 所使用的密钥是随机生成的, 与实际密钥没有任何关联, 如此DFA 分析工具提取出的密钥为实际密钥与NoisyRounds 的密钥的集合, 若要区分, 攻击者需将集合内密钥遍历, 而遍历空间与添加的NoisyRounds 组数n 成正相关.

3.2 NoisyRounds-WBAES 的设计与实现

NoisyRounds-WBAES 在Chow-WBAES 方案的基础上, 改变原第10 轮, 并添加若干组的Noisy-Rounds. 每组NoisyRounds 包含3 轮, 其中第2-3 轮和Chow-WBAES 的DFA 分析轮组在结构上是一致的, 并且NoisyRounds 使用的轮密钥是随机的. 为更好的描述NoisyRounds-WBAES 实现, 首先假定NoisyRounds 的组数为n, NoisyRounds-WBAES 的算法描述如算法1 所示. 将NoisyRounds-WBAES分为3 个阶段描述.

算法1 NoisyRounds-WBAES Input: P,ki,ˆki for i ∈0,··· ,10,rki for i ∈0,··· ,n, 其中P 为明文, n 为NoisyRounds 组数, ki 为主密钥K 的子密钥, ˆki 为ki 的ShiftRows 以后的结果, rki 为随机生成的轮密钥.Output: C = AES(P,K).1 State: R ←P; r ←1;2 while r ≤9 do 3 R = ShiftRows(R);4 R = AddRoundKey(R,ˆkr−1);5 R = SubBytes(R);6 ss R = MixColumns(R)7 end 8 R = ShiftRows(R);9 R = AddRoundKey(R,ˆk9);10 R = SubBytes(R);11 R = AddRoundKey(R,k10);12 r ←1;13 while r ≤n do 14 R = AddRoundKey(R,rkr−1);15 R = invSubBytes(R);16 R = AddRoundKey(R,rkr);17 R = invShiftRows(R);18 R = invMixColumns(R);19 R = MixColumns(R);20 R = ShiftRows(R);21 R = AddRoundKey(R,rkr);22 R = SubBytes(R);23 R = AddRoundKey(R,rkr−1);24 end 25 return R

· 1-10 轮: NoisyRounds-WBAES 的第1-10 轮和Chow-WBAES 的第1-10 轮的运算是一致的, 需要说明的是, NoisyRounds-WBAES 第10 轮在Chow-WBAES 的第10 轮基础上增加了AddRoundKey 和invSubBytes 步骤, 具体在NoisyRounds 抵消部分在描述.

其中i=0,1,··· ,15, invS 为AES-128 中S 盒的逆操作, rkr为随机生成的密钥.

对于一个字节的输入x, NoisyRounds-WBAES 中每轮的第1 列的TM-table 构造如下:

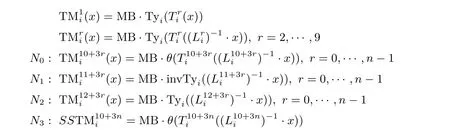
其中i=0,1,2,3. θ 为位扩展操作, 将8 位的输入转换为32 位的输出, θi(x) 有如下表示:

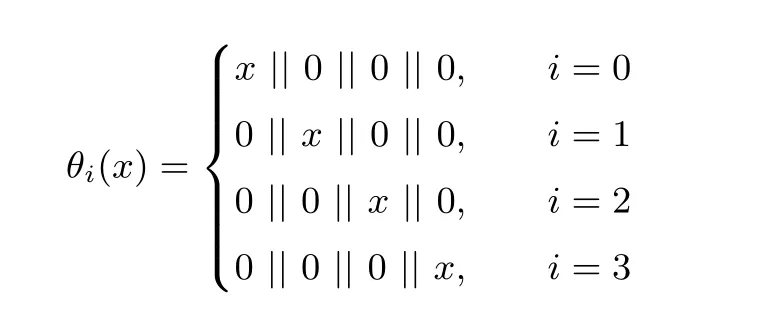
同样的, 需要额外的查找表操作来抵消MB 的影响以及添加r+1 轮的输入置换, 所以构造8 比特输入到32 比特输出的查找表BijBox. 对于一个字节的输入x, BijBox 有如下表示:

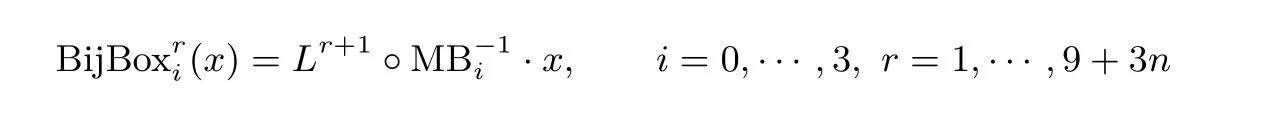
最终, NoisyRounds-WBAES 在应用了内部线性和非线性编码以后, 在NoisyRounds 组数为n 时,所需查找表数量如表2 所示, 共需存储开销168n+508 KB, 与Chow-WBAES 的存储开销相比, 每添加一组NoisyRounds, 存储开销增加30%, 而将故障注入正确位置的概率降低50%. 图3 展示了错误注入NoisyRounds 的N2和N3时的情况, 注入N2和N3时得到的错误密文与注入到实际第8 轮和第9 轮之间的到的错误密文与正确的密文相比, 都是存在4 个错误字节且这4 个字节有同样的排列规律, 这对于攻击者来说是不可区分的.

表2 NoisyRounds-WBAES 存储开销Table 2 Total storage requirement of NoisyRounds-WBAES

3.3 实验与安全性分析

在系统版本为Ubuntu16.4, GCC 版本为5.4.0, 内存大小16 G, CPU 型号为Intel(R) Core(TM) i7-7700 CPU@3.60 GHz 的实验环境中,运用Deadpool 工具对Chow-WBAES 与NoisyRounds-WBAES,包括两种算法增加非线性/线性的外部编码的情况进行DFA 实验.

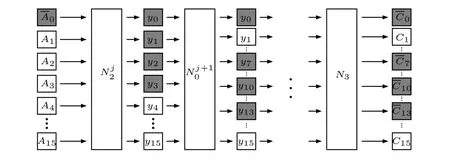
图3 针对NoisyRounds 的错误注入示意图Figure 3 Illustration of DFA attack to NoisyRounds

实验结果表3 展示了NoisyRounds 组数为1 的白盒AES 实现与Chow-WBAES 的对比结果, 结合表1, 我们发现有如下现象:

· NoisyRounds-WBAES 在一次遍历所需次数上小于Chow-WBAES, 这是因为Chow-WBAES 的查找表为实现为724 KB,可注入范围为bijBox8th和xor_table8th的部分空间,大小为160 Bytes,所以获得错误密文的概率为0.22%,而添加1 组NoisyRounds 后,可注入范围被扩大到320 Bytes,而查找表大小扩充到964 KB, 所以获得错误密文概率增大到0.32%, 从而破坏了Deadpool 分析工具的遍历优化算法. 图4 展示了在Deadpool 工具下有效错误密文、混淆错误密文以及无效错误密文随NoisyRounds 组数的关系, 其中无效错误密文是错误注入到了MB 置换造成符合规律的错误密文, 混淆错误密文是错误注入到NoisyRounds 后得到的错误密文, 而有效错误密文才是包含实际密钥信息的错误密文.

· 外部编码对DFA 攻击有抵抗作用. 通过实验发现, 外部编码对DFA 的抵抗作用主要为外部输出编码的影响, 因为外部输出编码可看成加密算法的秘密套件, 外部输出编码对于攻击者是未知的,并且外部输出编码不会在加密算法内部抵消, 所以攻击者无法绕过外部编码的影响. 现对带外部编码的WBAES 进行DFA 注入分析:

(1) 非线性外部输出编码: 假设明文Ai通过密钥K 加密得到经G 编码的密文, 再通过在A0注入一个字节的错误, 得到错误密文, 根据章节2.2.1 的推算方法可得:

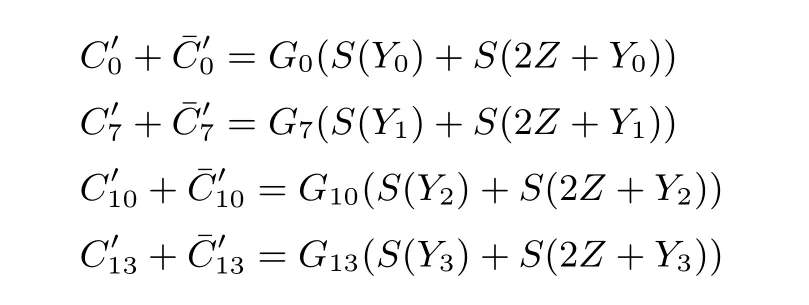
由于G0,G1,G2,G3未知, 无法确定Z 的集合, 所以该攻击平台不适用增加外部输出编码的白盒实现.

(2) 线性外部输出编码: 线性外部输出编码可以看作是对输出密文的128 比特到128 比特的置换,密文经过置换后一个错误的字节将影响大于等于个字节, 而四个字节将影响大于等于4 个字节, 被编码的密文最终不能够被分析工具当作错误密文收集并且无法分析, 所以无法应用此类方法还原密钥.

尽管NoisyRounds 使得Deadpool 平台的DFA 工具的遍历优化算法失效从而导致不能提取密钥, 但攻击者仍可以对白盒查找表进行全遍历注入, 进而获取所有的错误密文, 其中所有的无效错误密文, 混淆错误密文以及有效错误密文. 对于无外部编码的Chow-WBAES, 其查找表大小为508 KB, 逐个字节注入错误仅需2 小时即可完成. 因此我们假设攻击者已经通过全遍历注入获取到所有的错误密文, 由于加密程序和白盒查找表经过混淆以后, DFA 分析轮组对应的查找表在整个白盒表中的位置是未知的, 攻击者通过分析所有错误密文得到的密钥为所有NoisyRounds 的随机密钥以及真实密钥的集合.

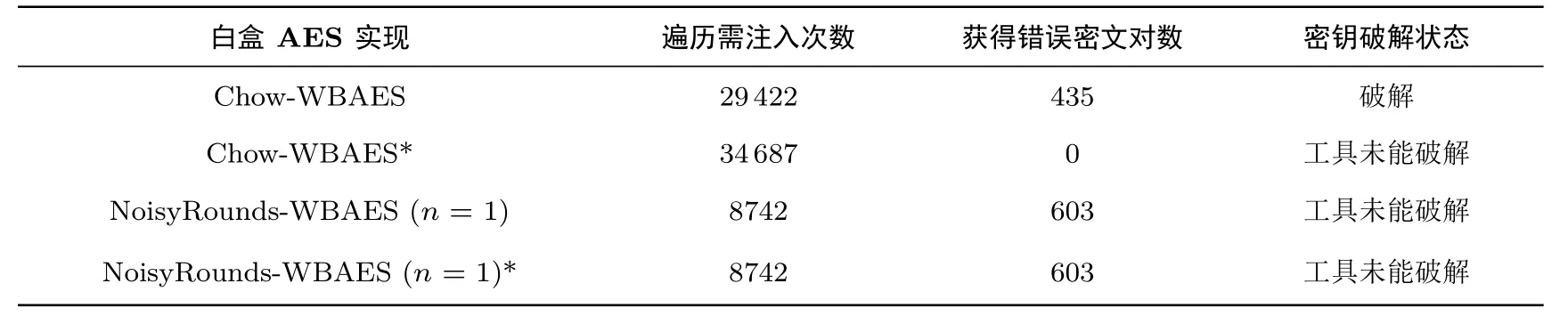
表3 基于Deadpool 工具的DFA 攻击结果Table 3 Result of DFA attack against multiple algorithms

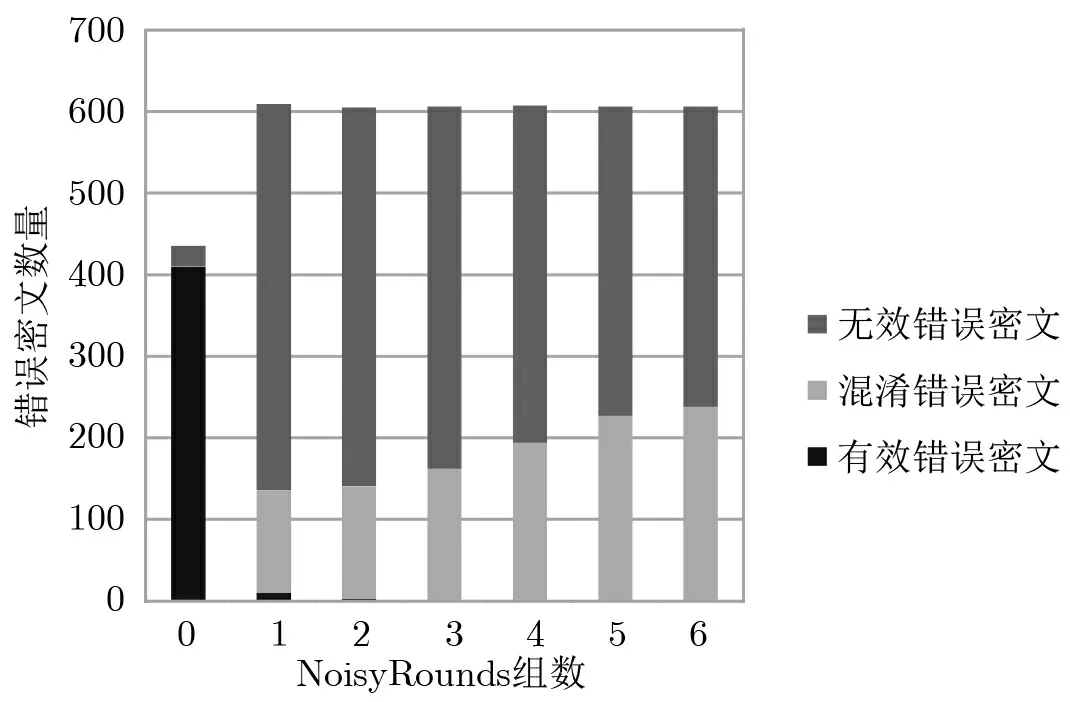
图4 错误密文对占比情况与NoisyRounds 组数关系图Figure 4 Distribution of fault ciphertext pairs

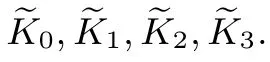
(1) 随机选择明文P, 运行白盒AES 加密程序E 得到密文C.

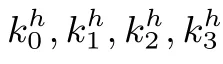
不难发现, 此种攻击模型下, 攻击者需要遍历候选密钥并执行加密程序(n+1)4次, 才能够提取出真实密钥, 而白盒查找表的大小随n 的变化呈正相关. 图5 展示了提取真实密钥所需遍历次数和白盒查找表大小随NoisyRounds 组数n 的变化关系.

4 结束语

虽然Chow 等人的白盒AES 实现方案存在多种破解手段, 但由于其实现代价小, 因此在实际中通过增加代码混淆等软件加固手段仍然得到广泛应用. 本文提出了一种基于NoisyRounds 保护的白盒AES实现方案, 该方案通过改变Chow 等人的白盒AES 算法的第10 轮结构, 并在其后增加能够混淆DFA 攻击分析的轮组来抵抗DFA 攻击. 实验与安全性分析表明, 该方案能够以计算复杂度为O(n4) 增大DFA针对白盒AES 攻击的难度, 而存储开销以线性大小增加. 如果在NoisyRounds 保护的基础上增加外部编码保护, 在外部编码未知的前提下，攻击者将不能通过DFA 分析来进行密钥恢复攻击. 本文工作对于提升Chow 类型白盒AES 的抗DFA 分析能力具有参考意义. 未来我们将尝试肖雅莹和来学嘉提出的16比特的内部编码的白盒AES 方案的DFA 分析和进一步研究NoisyRounds 技术对基于仿射变换的白盒SM4 实现的抗DFA 保护方案.

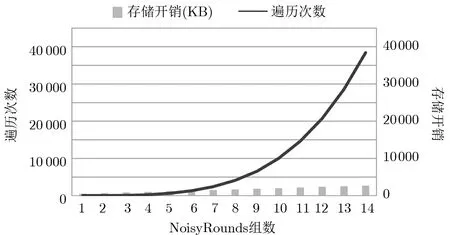
图5 遍历子密钥次数和存储开销与n 的变化关系图Figure 5 Relation between number of exhaustive search and storage cost