大规模监视下安全性定义再分析*

李 耕, 刘建伟, 张宗洋

1. 北京航空航天大学 网络空间安全学院, 北京100083

2. 空天网络安全工业和信息化部重点实验室, 北京100083

1 引言

2013 年的“棱镜门” 事件震惊全球, 美国前中央情报局职员爱德华· 斯诺登(Edword Snowden) 披露的信息以及其他证据显示, 美国国家安全局(National Security Agency, NSA) 等情报机构通过潜入各大网络巨头的服务器, 对全球网络进行大规模监视, 窃取美国本土及世界范围内的公民隐私信息以及重要领域通信信息[1,2]. 2020 年2 月, 美国、德国和瑞士媒体联合调查发现[3], 瑞士加密设备制造商Crypto 曾经由美国和德国情报机构秘密所有, 两家情报机构能够通过故意植入的漏洞破解使用该公司生产的加密设备传输的秘密文件, 而且, 此监控计划已经持续了数十年. 目前对于此事件的进一步调查正在进行中.

在此类事件中, 部分国家使用的一些窃密手段跳脱了传统密码学的考虑范畴, 一些在传统分析方法下被认为是安全的密码体制在新的环境下不再安全. 某些国家的情报机构可以通过对密码算法植入后门, 或在其执行中加入不安全因素, 以损害密码体制的安全性, 窃取用户敏感信息. 此类对密码体制的执行过程进行攻击的手段具有理论上的隐蔽性, 在相当长的时间内无法通过技术手段被发现. 例如, NSA 设计并强行通过了Dual_EC_DRBG[4]作为伪随机数生成器, 在Dual_EC_DRBG 相关标准推荐的参数里, 后门的拥有者可以在获取一定长度的随机数生成器的输出后, 预测后续输出[2]; 而对于不持有后门的实体,其输出可以达到一个伪随机数生成器的安全性.

新的安全威胁受到了密码学理论界的持续关注, 研究人员对大规模监视的攻击手段进行重新分析, 逐步建立了后斯诺密码学框架. 与传统密码学的重要不同在于, 后斯诺密码学刻画了敌手对密码算法进行“颠覆” 的过程, 即, 敌手可根据算法说明(specification), 通过嵌入后门等手段, 给出颠覆后的算法执行(implementation). 而算法执行对于使用者而言被建模为黑盒, 使用者无法获取其内部的运算过程, 只能通过输入输出来判断其是否诚实地按照算法说明执行. 早在“棱镜门” 事件发生之前, Young 等人[5]就已建立了kleptography 模型以刻画颠覆攻击, 并给出了相应安全性定义. Russel 等人[6]在Bellare 等人[7]和Degabriele 等人[8]研究的基础上, 给出了cliptography (改进的kleptography) 模型. 这些安全模型与相关的一系列研究普遍认为, 颠覆威胁下的密码体制需要达到这样的安全性: 除了本身能够实现传统密码学所定义的安全性外, 对于任何敌手给出的执行, 要么从用户角度能够区分其输出与算法说明的输出, 要么敌手自身也无法区分其输出与算法说明的输出. Russel 等人[6]将这种思想形式化表示为无隐写性(stego-freeness).

大规模监视背景下敌手的较强能力, 给安全密码体制的设计带来了很大挑战. 为了设计抗颠覆的密码体制, 在无隐写性即类似安全目标下, 研究人员提出了一系列针对颠覆攻击的防御方法, 主要可分为以下几类:

(1) 回归确定性算法: 如Bellare 等人[7]提出的“唯一密文(unique ciphertexts) 体制”.

(2) 基于可信元素: 如Mironov 等人[9]提出的密码反向防火墙(基于可信模块),和Fischlin 等人[10]提出的自守卫体制(基于可信阶段) 等.

(3) 基于随机喻言模型: 如Russel 等人[11]提出的基于“分割-融合模型” 的安全密码体制设计等.

(4) 基于(可信) 公开随机源: Ateniese 等人[12]提出的基于(可信) 公开的随机源的防御方法.

(5) 基于多源算法: Li 等人[13]提出的通过采用多个不同来源的算法构建抗颠覆密码体制的方法.

然而, 由于当前提出的这些防御方法存在各种各样的问题, 比如应用对象极其有限(确定性算法), 通过特定假设绕过了颠覆威胁下的关键问题(可信随机数产生), 需要借助于强假设(随机喻言), 需要复杂的工程实现方法及额外的成本开销(多源算法) 等, 在现实中的可行性均存在限制, 不适合于广泛应用. 虽然针对相关防御方法的研究已经有很多, 但仍缺少较好的解决方案, 本文重新审视了颠覆威胁下的安全模型和安全目标, 在拟合现实安全需求的前提下提出一种相对较弱的安全定义, 为设计可行性更强的防御方法提供方向和思路.

1.1 本文贡献

1.1.1 抗颠覆职能安全

本文从现实应用角度出发, 总结以往相关研究[8,12,14], 提出了抗颠覆安全保留性. 在实际中, 不同的应用场景对其中的密码体制有相应的安全要求(如语义安全, CPA 安全, CCA 安全等), 本文将其称为目标安全. 抗颠覆安全保留性的定义思想为, 在黑盒测试的保护下, 一个密码体制如果在遭到颠覆攻击时, 仍然能够实现特定场景下的目标安全, 则称其满足抗颠覆安全保留性. 抗颠覆安全保留性不再追求以无隐写性为代表的安全定义所要求的颠覆执行与算法说明不可区分, 而仅要求密码体制在颠覆环境下仍然能实现某种具体的安全性, 是一种较为直观的定义思路, 但契合了现实中对密码体制最直接的需求.

本文形式化分析了抗颠覆安全保留性与无隐写性之间的关系. 证明了所有同时满足目标安全和无隐写性的密码体制均满足抗颠覆安全保留性, 同时, 又通过构造安全性介于无隐写性和抗颠覆安全保留性之间的密码体制, 证明了抗颠覆安全保留性弱于无隐写性. 由此得出了图1 所示的逻辑关系. 由于抗颠覆安全保留性是最为直接的现实需求, 说明在逻辑上无隐写性定义过强. 在之前的研究中, 研究人员始终在图1 中的A 区, 即安全性达到无隐写性的区域构造抗颠覆密码体制, 而没有研究B 区中的密码体制. 目前在A 区并未得到可行性较高的抗颠覆防御策略, 因此抗颠覆安全保留性的提出, 对于拓宽抗颠覆密码体制设计思路, 探索防御方法具有一定现实意义.

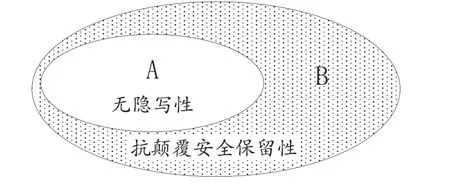
图1 无隐写性与抗颠覆安全保留性关系示意图Figure 1 Relationship between stego-freeness and security-preservation against subversion

1.1.2 算法隔离运行与抗颠覆密码体制设计

本文基于Russel 等人[6]提出的“分割-融合模型”, 探索在图1 中B 区设计密码体制的方法. 首先, 本文将密码系统中用户的输入信息, 如密钥, 明文等, 定义为业务数据, 并证明了在所有颠覆算法均能够获取业务数据(全知悉) 的条件下, 无隐写性与抗颠覆安全保留性的等价性, 由此为设计B 区的密码体制提供了方向, 即, 需要限制部分颠覆算法的知悉范围.

本文提出了算法隔离运行的概念. 算法隔离运行, 即在“分割-融合模型” 的框架下, 将部分分割后的子算法置于一个与用户业务数据“隔离” 的环境下运行. 算法隔离运行具有较强的现实可行性, 其简单的实现方法之一为在业务数据产生之前, 先运行被隔离的算法产生输出, 从而达到隔离的效果. 算法隔离运行排除了以“拒绝-采样攻击” 为代表的一类攻击方法成功的可能性.

基于算法隔离运行, 本文分别在部分颠覆模型和完全颠覆模型下设计了满足抗颠覆安全保留性的对称加密体制. 针对部分颠覆模型, 即密钥生成算法能够被安全执行, 但加解密算法处于颠覆威胁下的情况, 引入了带密钥的伪随机置换算法. 所设计的方案将随机数生成器和伪随机置换算法置于隔离运行状态, 以用户密钥作为伪随机置换的密钥, 对随机数生成器的输出进行置换并与明文进行异或, 将异或结果与置换前的随机数一同作为密文. 此设计没有达到无隐写性的安全性, 但是满足抗颠覆安全保留性, 且具有较强的可行性.

针对完全颠覆模型, 本文设计了两种方案. 方案一通过随机单比特生成器获取与均匀随机字串不可区分的随机字串, 继续采用上述框架构造安全体制. 方案二通过引入计算强提取器, 在密钥仅能保证一定的最小熵的情况下获取安全的随机字串, 与明文异或产生输出. 以上两种方案虽然采用了Russel 等人[11]设计的使用单比特随机源的方法, 但特点在于不需要保证密钥和加密过程中使用的随机数二者同时对于敌手计算上均匀随机, 这有利于降低密码体制的构建成本并提高算法执行效率.

1.2 相关研究

1.2.1 颠覆威胁下的安全模型研究

早在“棱镜门” 事件发生之前, Young 等人[5,15-17]就已对密码体制执行遭受敌手篡改的情况进行过研究, 他们将此类攻击方法概括为通用保护的内嵌后门(secretly embedded trapdoor with universal protection, SETUP), 并提出了kleptography 安全模型的概念. Young 等人[5]将SETUP 攻击区分为强SETUP、一般SETUP 和弱SETUP, 分别使用6 条规则概括其性质. 其后Young 等人[17]又通过游戏的方式形式化定义了强SETUP. Young 等人[5,15]针对常用的密码体制, 如RSA、El-Gamal、DSA、Kerberos 协议等设计了攻击方法并证明了其有效性.

Bellare 等人[7]提出了基于“检测-监视游戏” 的安全模型. 通过设计敌手参与的监视游戏和使用者参与的检测游戏, 定义密码体制在颠覆威胁下的安全性. 在文献[7] 的定义中, 如果监视优势可忽略或检测优势不可忽略, 则认为密码体制安全. Bellare 等人[7]假设颠覆的加密体制仍需要满足可解密性①所有由颠覆的加密算法产生的密文均可由纯净的解密算法正确解密要求, 在此基础上证明了唯一密文体制在颠覆威胁下的安全性. Degabriele 等人[8]认为文献[7] 中对于敌手的限制过强, 在不默认可解密性的前提下, 提出了输入触发攻击, 从而否定了确定性算法在颠覆攻击下的安全性.Degabriele 等人[8]在此基础上提出了改进的“检测-监视游戏” 的模型, 在此模型中, 检测者并不关注算法是否被篡改, 而仅关注敌手是否通过被颠覆的算法获取敏感信息. 在新定义的检测游戏中, 检测者可以获取监视游戏中的交互副本. Bellare 等人[18]参考Degabriele 等人[8]的观点, 改进了文献[7] 中的模型,对敌手提出了更高的要求, 要求其在监视游戏中能够返回完整的用户密钥.

Russel 等人[6]总结了文献[5,7,8] 等研究中安全性定义的思想, 提出了改进的kleptography 并命名为cliptography. cliptography 模型将检测算法抽象为一个概念-看门狗(watchdog). 根据强度不同, 看门狗分为离线看门狗(oラine watchdog), 在线看门狗(online watchdog) 和全知看门狗(omniscient 看门狗). Russel 等人[6]提出了无隐写性的安全目标, 即, 对于某密码体制以及其所有的执行, 要么不存在能够区分该执行的输出与算法说明的输出的PPT 敌手, 要么存在可以区分该执行与算法说明的看门狗.

Ateniese 等人[12]在对颠覆攻击的分析中引入了公开随机源, 并提出了相应的安全模型. 根据公开随机源性质的不同, Ateniese 等人将安全模型分为半私人、公共和透明三类. 在定义安全性时, Ateniese 等人将看门狗的检测优势与使用颠覆算法情况下在传统游戏中敌手的优势相比较, 如看门狗的优势始终大于敌手优势的常数倍, 则认为该密码体制安全. 此外, Ateniese 等人[12]把所有游戏分为约束性游戏和非约束性游戏, 以此决定在分析中选用离线看门狗还是在线看门狗.

此外, Ateniese 等人[19]、Dodis 等人[20]、Russell 等人[21]分别提出了针对颠覆威胁下签名体制、伪随机数生成器和随机喻言机的形式化安全模型.

1.2.2 颠覆威胁下的防御方法研究

Bellare 等人[7]将所有明文最多只对应唯一合法密文的加密体制定义为唯一密文体制, 并证明了唯一密文体制在“检测-监视游戏” 中的安全性.

Mironov 等人[9]提出了密码反向防火墙(cryptographic reverse fire, CRF) 的概念. CRF 是部署于用户密码系统与外部之间的设备, 对所有用户与外界交互的信息进行处理. CRF 的特殊性在于, 一方面其被假设为是不可颠覆的, 即一定能够诚实地执行相应算法; 另一方面, CRF 又被假设为公共设备, 不可获取用户的隐私信息(如密钥等). Mironov 等人[9]通过功能保留性, 安全保留性与抗泄露性对CRF 进行了形式化定义. Dodis 等人[22]继续针对CRF 定义了检测可失败的概念, 并利用再随机化加密体制为消息传输协议中的双方设计了CRF 的通用构造方法. Chen 等人[23]在平滑映射哈希函数[24]概念的基础上提出了可延展平滑映射哈希函数, 并基于此设计了CRF 的通用构造方法.

Fischlin 等人[10]提出了自守卫密码体制. 其安全性基于一个假设可信的运行阶段, 称为“安全启动阶段”. 在安全启动阶段中使用者可运行可信的算法获取部分随机元素, 在其后的运行阶段这些随机元素可被调用. Fischlin 等人[10]对El-Gamal 等常用密码体制设计了自守卫密码体制的构造方法.

Russel 等人[11]设计了“分割-融合模型”, 将一个完整的密码算法分割为若干个子模块, 所有子模块融合在一起实现原算法的功能. Russel 等人在cliptography 模型下, 通过引入随机喻言模型, 设计了具有无隐写性的密码体制的通用构造方法. 此外, Russel 等人还在子模块个数可以不为常数的前提下, 设计了无需随机喻言机的无隐写密码体制.

Horel 等人[25]在抗颠覆防御方法的设计中引入了隐写体制的思想. 他们利用颠覆的加密算法对于除监视者本身以外的实体仍需要满足特定安全性的性质, 设计了一种消息传输协议, 将真正需要传输的消息嵌入到密文中, 从而在通信双方之间建立“潜信道”. Horel 等人的方案实现了当监视者能够对密文进行解密的情况下, 被嵌入了消息的副本仍然与正常执行颠覆算法产生的副本计算上不可区分.

Ateniese 等人[12]设计了通过引入一个公开的随机源实现防御的方法. 分别在公开随机源产生的随机数: (1) 可信但可被敌手获知; (2) 可信但可被敌手和颠覆算法获知; (3) 不可信的情况下, 设计了颠覆威胁下安全密码体制的通用构造方法.

Li 等人[13,26]设计了通过采用来源于不同监视者的算法执行构造抗颠覆的密码体制的方法. 在不同敌手完全隔绝的情况下, Li 等人[13]设计了一种安全的消息传输协议, 能够实现协议的副本对于所有敌手,要么与算法说明的输出不可区分, 要么与诚实地执行该敌手给出的颠覆执行产生的副本不可区分. 在不同敌手之间可通过不同形式进行有限交流的情况下, Li 等人[26]分别基于“分割-融合模型” 设计了满足无隐写性的对称密码体制的构造方法.

1.3 本文组织结构

第2 节介绍了本文中使用的主要表示方法即相关预备知识. 第3 节提出了抗颠覆安全保留性的概念,并形式化分析了其与无隐写性定义之间的关系. 第4 节提出了算法隔离运行的概念, 并论证了其在特定条件下的必要性. 第5 节分别在部分颠覆模型与完全颠覆模型下, 基于算法隔离运行的方法设计了满足抗颠覆安全保留性的对称加密体制.

2 预备知识

2.1 表示方法定义

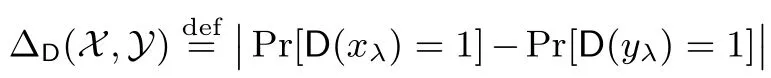
2.2 随机数生成器

定义1 给出了随机数生成器的形式化定义方法. 为了合理简化分析, 本文忽略了除安全参数以外的随机数生成器的其他输入.

定义1令随机数生成器Rg 的输入为安全参数λ, 输出为ℓ 比特随机字串. 如果对于所有的PPT 敌手A, r ←Rg(λ), 有

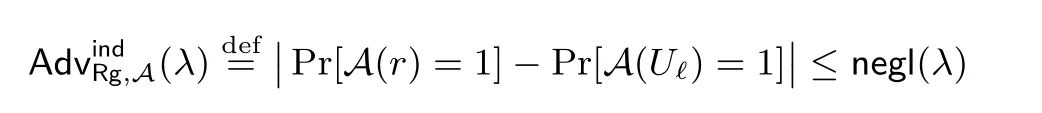
则称Rg 满足不可识别性.

2.3 伪随机置换

本文使用了文献[27] 中对于伪随机置换算法的定义.

定义2[27]令PER={Pers} (s ∈S) 为{0,1}ℓ上带有密钥的置换, Πℓ代表{0,1}ℓ上所有置换的集合. 如果对于所有的PPT 敌手A,

则称PER 为伪随机置换.

2.4 无隐写性

Russel 等人[11]定义了密码算法在颠覆威胁下无隐写性的概念, 本文使用其通用形式, 具体地,

定义3[11]考虑算法说明为Fspec的算法F, 如果存在看门狗算法W, 对于所有参与如图2 中游戏的PPT 敌手A, 其中Fimpl为对应于算法说明Fspec的执行, IG 为算法应用的输入变量生成器.

其中

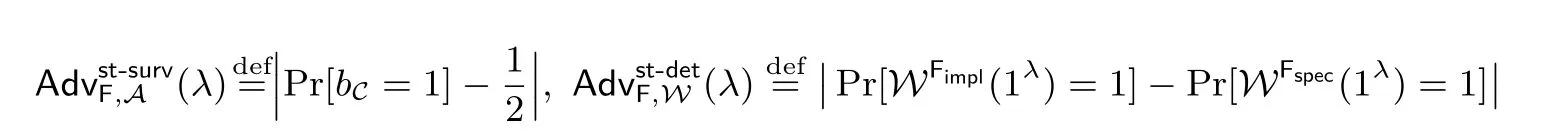
则称Fspec满足无隐写性.

2.5 IND-CPA 安全

定义对称密码体制的IND-CPA 安全性如下:

定义4记对称加密体制SE={K,E,D}, 其中K:1λ→K 为密钥生成算法, E:K×M →C 为加密算法, D:K×C →M 为解密算法. 定义

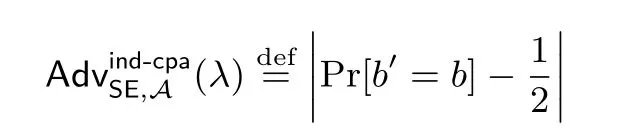
其中, 游戏IND-CPA 如图3 所示, 则称密码体制SE 满足IND-CPA 安全.

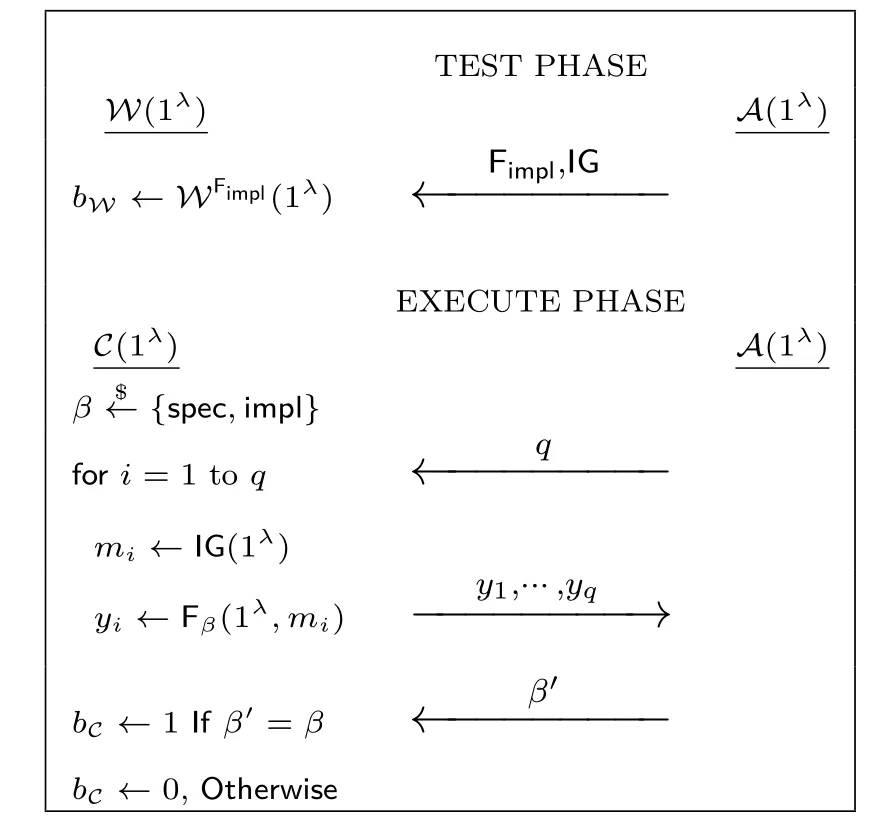
图2 无隐写性游戏(通用形式)Figure 2 Game for stego-freeness (general form)

图3 IND-CPA 游戏Figure 3 Game for IND-CPA

3 密码体制的抗颠覆安全保留性

相对于当前普遍使用的刻画颠覆威胁下密码体制安全性的无隐写定义, 本节结合相关研究, 提出了抗颠覆安全保留性. 第3.1 节给出了抗颠覆安全保留性的形式化定义, 第3.2 节分析了其与无隐写性之间的关系, 并证明了满足抗颠覆安全保留性的密码体制要多于满足无隐写性的密码体制.

3.1 密码体制的抗颠覆安全保留性

为了刻画颠覆威胁下密码算法的安全性, 本节形式化定义了密码体制的抗颠覆安全保留性. 安全保留性的定义思想较为直观, 相对于Russel 等人在文献[6] 中提出的密码体制的无隐写性(详见定义3), 其不再要求被颠覆的密码执行的输出与纯净算法的输出计算上不可区分, 而仅仅要求密码体制即使在被颠覆的情况下仍能实现原体制的具体安全性. 实际上, 在Degabriele 等人[8]、Ateniese 等人[12]和Chow 等人[14]对于颠覆威胁下密码体制的安全分析中, 也使用了此种思路定义了若干种具体的安全性, 本文所提出的抗颠覆安全保留性可视为对此类安全定义的通用形式表达.

为了涵盖现实中各种不同权限的监视者,本模型兼顾部分颠覆和完全颠覆两种情况②如果监视者能够颠覆密码体制中的所有算法, 则称为完全颠覆; 如果监视者仅能够颠覆密码体制中的部分算法(例如在加密体制中能够颠覆加解密算法, 而不能颠覆密钥生成算法), 则称为部分颠覆.,并使用了“分割-融合模型”[11]中的分析思路. 设密码体制Π 在执行中被拆分为若干个模块{I1,I2,··· ,In,S1,S2,··· ,Sn},其中, Ii为暴露于颠覆威胁下的模块(若考虑完全颠覆, 则无Si). 本模型仍然使用Bellare 等人[7]监视游戏加检测游戏的框架, 具体的:

监视游戏:由挑战者和监视者参与. 其中监视者根据其行为被划分成两个阶段, 第一阶段的监视者用A1表示, A1根据相关算法的说明, 产生对应的颠覆执行. 第二阶段的监视者用A2表示, A2与挑战者运行一般的安全定义游戏, 游戏中挑战者访问的是经过颠覆后的密码体制, 这一过程用A2(·)G⇆C^F(·)(·) 简化表示, 其中为经颠覆的算法执行. 具体的, 定义监视者的监视优势:

其中监视游戏SURV 如图4 所示, γ 为常数.

检测游戏:安全保留性的定义沿用了Russel 等人[6]cliptography 模型中在线看门狗的概念. 检测游戏由挑战者和看门狗参与, 看门狗试图在游戏中判断挑战者给出的黑盒算法是纯净的算法还是经监视者颠覆的算法. 具体的, 定义看门狗的检测优势:

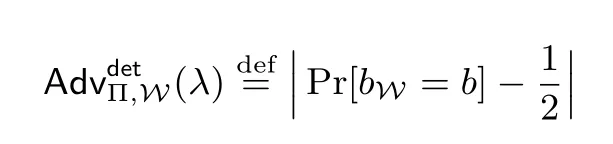
其中检测游戏DET 如图4 所示.

图4 抗颠覆安全保留性定义游戏Figure 4 Games for definition of security-preservation against subversion

基于监视优势和检测优势, 定义密码体制的抗颠覆安全保留性:

3.2 安全保留性与无隐写性的关系

从定义形式上看, 无隐写性强调颠覆执行与算法说明之间的对比, 以二者对敌手的不可区分来定义颠覆威胁下的安全性. 其定义过程并不体现密码体制要实现的具体安全目标. 安全保留性则从密码体制旨在实现的具体安全性出发, 仅对颠覆执行进行分析. 鉴于在颠覆攻击发生的情况下, 用户信息的安全性取决于颠覆执行的安全性, 因此抗颠覆安全保留性是一种更为直观的定义方式, 直接刻画了现实安全需求.

cliptography 主要关注密码体制被不诚实执行时的安全性, 因此相关研究都默认作为研究对象的密码体制被诚实执行时是安全的. 在此前提下, Russel 等人[6]定义的无隐写性不弱于3.1 节中密码体制的安全保留性. 详细定理描述如下.

定理1如果密码体制Π 的说明是(G,γ) 安全的, 且其能够满足无隐写性, 则其一定满足抗颠覆-(G,γ)-安全保留性.

证明:假设Π 不满足抗颠覆-(G,γ)-安全保留性, 即存在PPT 敌手A = (A1,A2), 对于所有PPT算法W, 有则可以构造PPT 敌手A′= (A′1,A′2), 其调用敌手A 以攻破密码体制Π 的无隐写性. A′具体可采取以下策略:

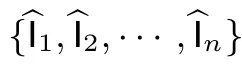
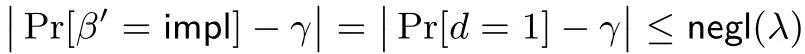
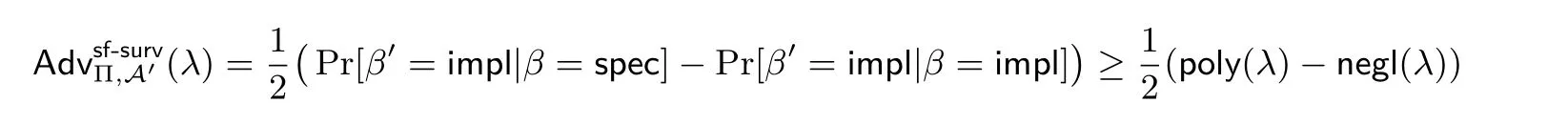
因此, Π 也不满足无隐写性, 定理1 得证.

另一方面, 如果某密码体制不满足无隐写性, 则必定存在这样的颠覆执行, 能够通过其输出向监视者至少泄露一比特信息. 在此类情况下, 如果密码体制中所有的颠覆算法都能够掌握用户的关键隐私信息,则密码体制显然亦不满足抗颠覆安全保留性(相关证明详见第4.1 节). 然而, 如果在密码系统的工程实现过程中采取一定措施, 以限制算法执行的信息知悉范围, 则有可能实现不满足无隐写性但满足抗颠覆安全保留性的体制, 具体的定义及设计详见第5 节. 因此, 综合本文论据, 密码体制无隐写性的安全性要高于抗颠覆安全保留性, 此方面具体讨论见第6 节.

4 算法隔离运行

本节提出了算法隔离运行的防御方法. 第4.1 节证明了在所有颠覆算法都能够获取全部用户数据的情况下, 不满足无隐写性的密码体制也不满足抗颠覆安全保留性, 此否定性结论表明了限制部分颠覆执行知悉范围对于设计可行性更强的抗颠覆防御方法的是非常必要的. 第4.2 节给出了算法隔离运行的形式化表示方法.

4.1 颠覆算法全知悉条件下的否定性结论

本文的主要目的之一在于重新审视cliptography 模型[6]中算法无隐写性安全目标的现实合理性, 试图在保证算法实际安全的前提下, 适当下调颠覆威胁下的安全目标, 为设计更加实用的抗颠覆防御策略提供理论基础. 第3.1 节提出了抗颠覆安全保留性的概念, 并形式化证明了抗颠覆安全保留性是算法无隐写性的必要条件. 然而, 在密码算法的实现过程缺少特定限制的情况下, 难以保证抗颠覆安全保留性真正弱于无隐写性, 而体现其实际意义.

本节以对称加密算法为例. 记对称加密体制SE={K,E,D} 的目标安全为IND-CPA(详见定义4), 其中K:1λ→{0,1}κ为密钥生成算法, E:{0,1}κ×{0,1}ℓ→{0,1}n为加密算法, D:{0,1}κ×{0,1}n→{0,1}ℓ为解密算法. 为了使结论更具一般性, 考虑部分颠覆, 即仅加密算法E 处于颠覆威胁下的情况(全颠覆模型亦包含此种情况). 针对加密算法E, 我们将密钥k 与消息m 记为业务数据. E 在“分割-融合模型” 下被分割为若干子算法{Sub-Ei}. 可以证明在所有子算法均可获取业务数据时, 如果SE 不满足无隐写性, 则其亦不满足抗颠覆安全保留性. 因为此时可以利用攻破无隐写性的颠覆执行, 逐比特泄露用户的密钥. 详细定理描述如下.

定理2对于目标安全为IND-CPA 的对称加密体制SE, 如果加密算法E 的所有子算法{Sub-Ei} 的执行均可获取业务数据(k,m), 则如果SE 不满足无隐写性, 其亦不满足抗颠覆-(IND-CPA,1/2)-安全保留性.

证明:假设存在PPT 敌手A, 能够破坏SE 的无隐写性, 则可构造PPT 敌手A′, 其模拟挑战者与A 运行无隐写游戏, 破坏SE 的抗颠覆-(IND-CPA,1/2)-安全保留性. A′具体执行以下策略:

由定理2 及定理1 可知, 在颠覆算法对用户业务数据全知悉的情况下, 不可能构造安全性介于无隐写性与抗颠覆安全保留性之间的密码体制. 因此对颠覆执行的知悉范围进行限制, 是构造实用性更强的抗颠覆攻击防御方法的思路之一.

4.2 算法隔离运行模型

为了设计更加实用的抗颠覆防御策略, 构造属于图1 中B 区的密码体制, 本节在“分割-融合模型” 的基础上, 提出算法隔离运行的密码体制工程实现方法. 其基本思想为在对密码算法进行分割后, 将部分子算法的执行置于一个与用户业务数据“隔离” 的环境下运行, 即, 使之无法接触用户的密钥、消息等关键信息.

关于如何实现算法隔离运行, 较为简单的思路之一为对相关算法进行预先运行, 即, 在用户私钥、明文产生之前, 先运行被隔离的算法获取其输出, 此举实际上避免了相关算法得到用户敏感信息. 此外, 通过密码系统内部硬件隔离、控制被隔离算法可读取的信息列表等方法也能够实现算法隔离运行的效果, 相关具体工程实现手段超出了本文讨论的范畴, 在此不做具体讨论.

5 基于算法隔离运行的抗颠覆安全保留的对称密码体制

本节基于算法隔离运行思想, 通过引入伪随机置换、计算强提取器等工具, 在第5.1节和第5.3节中分别在部分颠覆模型和完全颠覆模型下设计了抗颠覆安全保留的对称加密体制, 并在第5.2节和第5.4节中给出了相应的安全性分析.

5.1 部分颠覆模型下基于隔离运行的对称密码体制设计

本节考虑部分颠覆模型下的对称密码体制设计. 其中假设密钥生成算法可以被诚实执行, 而加密算法和解密算法处于颠覆威胁下. 在本方案的设计中引入了第2.3 节中定义的伪随机置换. 加密算法E 被分割为以下两个部分:

- Rg:1λ→{0,1}ℓ, 随机数生成器, 其算法说明满足定义1中的不可识别性.

图5 算法隔离运行Figure 5 Isolated operation of cryptographic scheme

- Per : {0,1}κ× {0,1}ℓ→{0,1}ℓ, 伪随机置换算法, 其算法说明满足定义2 中的安全性. 其中{0,1}κ为密钥空间.

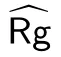
图6 部分颠覆模型下基于隔离运行的对称加密算法和解密算法Figure 6 Symmetric encryption algorithm based on isolated operation in partial subversion

5.2 安全性分析

在隔离运行假设的基础上, 图6 中的加密体制仍能在颠覆威胁下保证IND-CPA 安全性. 详细定理描述如下.

定理3图6 中的加密体制在部分颠覆模型下满足抗颠覆-(IND-CPA,1/2)-安全保留性.

证明:假设定理3 不成立, 即, 存在PPT 敌手A, 对于任何的PPT 看门狗W, 使得

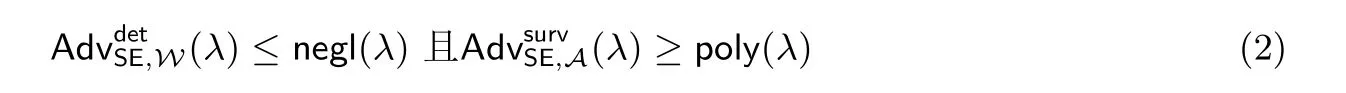
其与式(2) 矛盾, 命题得证.

5.3 完全颠覆模型下基于隔离运行的对称密码体制设计

本节继续讨论在完全颠覆模型下基于隔离运行的对称密码体制的构造. 完全颠覆指密码体制中包括密钥生成算法在内的所有算法均处于颠覆风险下, 这给抗颠覆密码体制的设计带来了更大的难度.

为了在缺少可信随机源的情况下获取计算上均匀随机的字符串, Russel 等人[11]设计了使用非常数个随机单比特生成器产生随机字符串的方法, 即, 无状态的单比特随机源每次仅输出一个随机比特, 将多次输出串联, 可得到一个与均匀随机字符串统计不可区分的随机串. 详细描述如引理1,

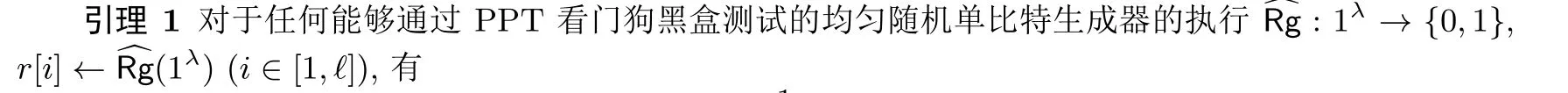
其中ϵ 为λ 的可忽略函数.

引理1 的证明详见文献[11] 附录D, 本文中不再重复. Russel 等人[11]基于引理1 中的方法获取计算上均匀随机的密钥和随机数, 构造了抗颠覆安全的加密体制. 本节设计的方法与Russel 等人设计的方案有类似之处, 但重要区别之一在于, 本节的方案不需要保证密钥和加密过程中产生的随机数二者同时计算上均匀随机, 而只需要保证其中一个与均匀随机字串不可区分, 另一个满足高熵值的条件即可. 相比于Russel 等人的设计, 这样有效减少了单比特随机源的使用数量, 降低了密码体制的实现成本和运行效率.

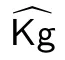
图7 完全颠覆模型下基于隔离运行的对称加密算法和解密算法Figure 7 Symmetric encryption/decryption algorithm based on isolated operation in complete-subversion

由此, 基于定理3 和引理1, 能够直接给出定理4.

定理4图7 中的加密体制在完全颠覆模型下满足抗颠覆-(IND-CPA,1/2)-安全保留性.

此外, 本节设计了另一种满足抗颠覆安全保留性的对称密钥体制构造方法, 其中用户的对称密钥不再与均匀随机字串计算上不可区分,而只能保证a-bit 的最小熵. 本节针对此情况下的设计,参考了Ateniese等人在文献[12] 中引入计算提取器(computational extractor) 的思想.

定义6[12]如果对于所有最小熵为a 的随机变量X ∈{0,1}n, 和所有运行时间为t 的识别算法D,哈希族H:{hs:{0,1}n→{0,1}m}s∈{0,1}ℓ满足

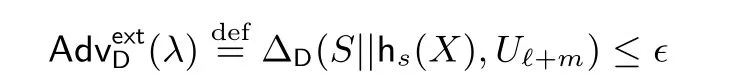
其中ϵ 为λ 的可忽略函数, 则称其为(n,m,a,t,ϵ)-计算强提取器族.

Guruswami 等人[28]证明了计算强提取器族的存在性并给出了其具体构造.

加密体制被分割为以下若干模块:

- Kgen:1λ→{0,1}n/a, 密钥生成子算法, 产生n/a-bit 的均匀随机字符串.

- Rg:1λ→{0,1}, 单比特随机数生成器, 其算法说明满足第2.2 节中定义的不可识别性.

- hr:{0,1}n→{0,1}m, (r ∈{0,1}ℓ), (n,m,a,t,ϵ)-计算强提取器.

图8 完全颠覆模型下基于隔离运行的对称加密体制Figure 8 Symmetric encryption algorithm based on isolated operation in complete-subversion

5.4 安全性分析

在隔离运行假设的基础上, 图8 中的加密体制仍能在颠覆威胁下保证IND-CPA 安全性. 详细定理描述如下.

定理5图8 中的加密体制在部分颠覆模型下满足抗颠覆-(IND-CPA,1/2)-安全保留性.

证明:假设定理5 不成立, 即, 存在PPT 敌手A, 对于任何PPT 的看门狗W, 使得

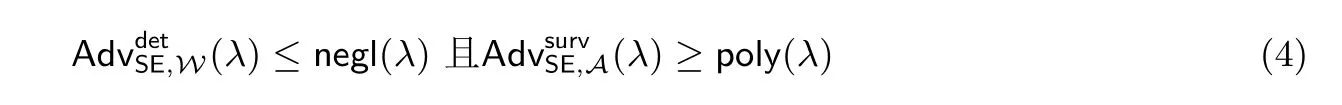
其与式(4) 矛盾, 命题得证.

采用第5.2 节中描述的基于“采样-拒绝” 的攻击方法, 同样可以证明图7 和图8 中的加密方案并不满足无隐写性. 因此第5.3 节中两种方案的安全性也介于抗颠覆安全保留性与无隐写性之间.

6 结论

为了分析颠覆威胁下密码体制的安全性, 本文提出了抗颠覆安全保留性的概念. 抗颠覆安全保留性要求所有能通过黑盒测试的颠覆执行均能实现原定的目标安全性. 相比于当前普遍使用的用于分析颠覆攻击的无隐写性, 抗颠覆安全保留性从定义形式上更加直接地反映了现实需求.

一方面, 本文形式化证明了所有满足无隐写性的密码体制均满足抗颠覆安全保留性. 另一方面, 本文通过设计算法隔离运行的防御策略, 构造了安全性介于无隐写性与安全保留性之间的密码体制, 证明了无隐写性集合是抗颠覆安全保留性集合的真子集. 综合以上论据, 可以得出如图1 所示的逻辑关系.

在现有针对于大规模监视的研究中, 研究人员始终试图在A 区构造密码体制, 而忽略了B 区的存在.鉴于当前针对A 区缺少可行性较高的防御方法, 而以算法隔离运行为代表的针对B 区的防御方法具有较强的现实可操作性, 因此抗颠覆安全保留性的提出, 对于重新审视并调整颠覆威胁下的安全目标, 构建更加实用的抗颠覆密码体制, 具有重要的意义.