倍点运算的白盒化实现及应用*

潘文伦, 张立廷

摩石实验室, 成都卫士通信息产业股份有限公司, 北京100070

1 引言

密码算法的运行环境对其安全性有重要影响. 传统的密码设备需要在安全可信环境中运行, 算法的内部状态必须绝对保密, 不能够被外部获知, 这通常被称作黑盒模型. 随着密码技术应用的多样化, 密码产品特别是密码软件产品所处的运行环境越来越不可控, 在极端环境下, 攻击者甚至具有完全控制算法运行过程、监控干扰算法运行、提取运算中间信息等能力, 例如在数字版权保护等应用场景中, 恶意用户在手机、电脑等终端使用运营商提供的数字资源服务时, 可能监控数字资源在终端的解密过程, 恢复密钥进而获取受版权保护的资源, 此类极端环境被称为白盒攻击环境[1]. 在白盒攻击环境中, 传统实现的密码算法毫无安全性可言, 攻击者通过控制算法运行过程, 提取算法中间运算信息等, 可以轻易恢复出完整的密钥, 彻底破坏算法的安全性.

2002 年, Chow 等提出白盒攻击环境概念时, 设计了首个AES、DES 白盒实现方案[1,2], 其主要思想是利用分组密码迭代运算的特点, 将密码算法运算过程进行分解, 将其中部分运算结合起来转换成查找表,以查表的方式完成计算, 将轮密钥嵌入到查找表中并通过随机映射保护查找表, 以实现保护每一轮轮密钥.基于Chow 等的白盒设计思想, 人们提出了一系列标准密码算法如AES、DES、SM4[3-7]等的白盒实现方案. 然而, 这些方案都在提出不久后就被攻破[8-10], 且大多性能低下, 难以满足实际应用需求. 基于白盒攻击环境的特点, 人们也设计了一些新型白盒密码算法, 如基于ASASA 结构[11]、SPACE-Hardness 问题[12]、白盒密钥[13]等的白盒算法, 相比于对标准算法的白盒实现, 这些新型算法在效率、安全性方面具有一定优势, 但缺乏实际应用.

目前, 公钥密码在白盒环境中的密钥防护成果相对较少. 2014 年, 林璟锵等采用多方安全计算的思想,设计了SM2 签名算法的“云加端” 方案[14]. 在该方案中, 用户端和云端分别独立产生部分私钥信息, 通过设计的交互协议协同生成公钥, 两方联合完成SM2 签名、解密运算, 却无法获取对方的私钥信息, 从而达到保护私钥的目的. 之后, 人们基于该思想构造了系列密钥分割方案, 对通信量、效率等进行优化[15],还有针对不同应用场景的扩展方案[16]. 2018 年, 候红霞等构造了安全的两方协作SM2 签名方案[17], 该方案采用零知识证明技术认证双方身份, 用承诺技术保证输出完整签名的正确性, 用同态加密技术、时戳机制等确保只有在特定条件下才能输出正确的完整的签名, 具有更高的安全性, 可在通信信道不安全的环境中使用. 2020 年, Yudi Zhang 等提出了基于同态加密的SM2 协同签名算法[18], 可实现在不恢复签名私钥的情况下完成SM2 签名, 并给出了可证明安全保障. 对于单一主机上公钥密码白盒实现研究, 2018年, 谷大武等提出了SM2 白盒签名方案[19], 通过构造参数表、组合产生随机数等方式保护私钥安全, 但该方案不支持标准SM2 签名输入输出接口, 且需要额外的辅助信息才能完成验签过程. 一些商业公司如爱迪德[20]等宣称开发了ECC、RSA 等公钥密码白盒产品, 但作为商业秘密并未对外公开技术细节.

本文针对公钥密码算法中的常见运算-椭圆曲线倍点运算, 构造了白盒实现方案, 以保护倍数(私钥等秘密) 信息. 我们的主要策略是: 首先将倍数信息展开成特定的表达形式, 然后对展开后的每个分量分别构造查找表, 以保护每一分量信息, 然后通过网络化查表的方式消除每个查找表的编码信息, 最后实现最终结果的正确计算, 整个过程不泄露分量信息, 进而实现对倍数信息的保护. 进一步, 我们使用余数系统嵌套分解大数运算, 以实现查找表的分解, 从而降低查找表的规模, 使白盒方案所需存储空间满足实际应用需求. 最后, 我们基于此构造了SM2/9 白盒解密方案, 并将此思想推广到模幂运算的白盒实现, 进一步应用到RSA 等算法的白盒实现.

2 符号约定

3 基本思路

倍点运算Q = [d]C 是椭圆曲线公钥密码算法中的常见运算, 算法的安全性通常依赖于密钥的保密,椭圆曲线倍点运算的单向性为此提供了基本保障, 即给定点Q,C, 恢复倍数信息d 在计算上不可行. 为完成该计算过程, 现实中人们通常将该运算过程分解成多个点加运算, 如先将d 展开

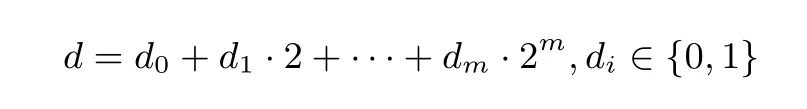
然后依次计算

从而可通过依次计算两点相加, 完成点C 的d 倍点运算, 其中, Qm=[dm]C,Q=Q0.

当倍点运算运行在不可信平台上时, 攻击者具有监控甚至干扰整个计算过程的能力, 因此可根据上述运算过程轻易依次获取每个di, 进而恢复d. 为保护倍数信息d, 我们可以将运算过程Q=[d]C 制作成查找表, 即预先将点C 的每个取值按顺序遍历, 依次存储其倍数Q, 构成一张查找表Lookup_Table, 然后当输入信息C 时, 根据C 的取值查询Lookup_Table, 即可得到其倍点Q. 在白盒攻击环境下, 攻击者只能获取到查找表Lookup_Table 的信息, 由于倍点运算的单向性, 攻击者无法据此恢复d, 从而实现对d的保护. 该方法虽然简单有效, 但由于点C 的取值范围很大, 如若C = (x,y,z) ∈E(Fq), 当E(Fq) 的阶为N 时, 查找表Lookup_Table 的规模将达到3q·2N比特, 无法在实际中存储该查找表, 因此, 将倍点运算白盒化实现的首要目标是研究如何分解上述查找表以降低存储规模.

Chow 等提出的AES、DES 白盒实现方案有以下三点主要思想: (1) 利用分组密码迭代结构特点将算法分解, 并将分解后每一块计算过程转换成查找表, 以查表的方式完成计算; (2) 将轮密钥嵌入查找表, 并使用随机置换保护查找表, 以保护每一轮的轮密钥; (3) 使用小规模置换(如4 比特置换) 级联组合成较大规模的置换(如32 比特置换), 以实现对查找表的分解, 降低存储规模.

我们借鉴该思想来构造倍点运算的白盒实现方案: 首先将倍数信息分解, 以实现对倍点运算的分解,然后将分解后的每一块转换成查找表; 其次, 将倍数分解后的每块信息嵌入到查找表中, 并使用随机置换保护查找表, 以保护倍数信息分解后的每个分量的信息; 最后, 采用小规模置换实现对每个查找表的分解,使所需存储空间降低至现实可用的范围.

若我们按如下方式分解倍数信息d

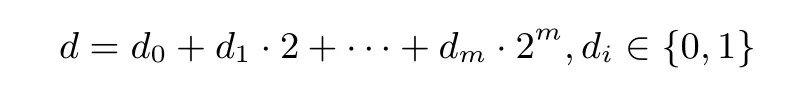
并将点加运算Qi−1=[di−1]C+[2]Qi中含有信息di−1的运算部分转换成查找表并编码保护

其中, F 为随机置换. 此时, 由于di−1∈{0,1}, 攻击者选择两组((x0,y0,z0),(x1,y1,z1)) 查询该查找表,根据查询结果是否变化就可判断出di−1的值, 因此我们不能将倍数d 简单地按上述形式展开.

考虑到倍点运算和点加运算的复杂性, 为使查找表Lookup_Table 不泄露di−1的值, 我们将d 表示成±1 的形式, 即di−1∈{1,−1}. 此时, 由于[di−1](x,y,z) = (x,di−1y,z), 对任意由函数F 与di−1生成的查找表Lookup_Table, 均存在随机置换F′与−di−1可以生成相同的查找表, 从而攻击者无法根据给定的查找表区分出di−1的取值. 因此, 我们首先将倍数d 展开成如下形式

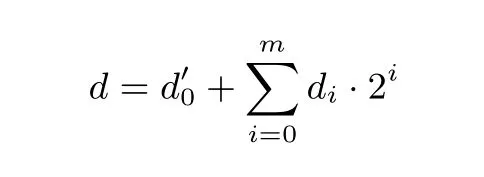
算法1 Expand(d)Input: d Output: {d′0,d0,d1,··· ,dm}1 tag = d % 4;2 switch tag do 3 Case 0:4 d′0 = 1,d0 = 1,d1 = −1;5 Case 1:6 d′0 = 2,d0 = 1,d1 = −1;7 Case 2:8 d′0 = 1,d0 = −1,d1 = 1;9 Case 3:10 d′0 = 2,d0 = −1,d1 = 1;11 end 12 for i = 2 to m do 13 if (d ≫i) % 2 == 0 then 14 if di−1 == 1 then 15 di−1 = −1,di = 1;16 end 17 else 18 di−1 = 1,di = −1;19 end 20 end 21 else 22 di = 1;23 end 24 end

算法2 Mul_Point(C)Input: C Output: Q,Q = ∑m−1 i=0 [di ·2i]C 1 R0 = [d0]C;2 Q0 = R0;3 for i = 1 to m −1 do 4 Ri = [2didi−1]Ri−1;5 Qi = Qi−1 +Ri;6 end 7 Q = Qm−1;

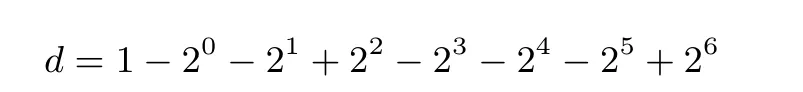
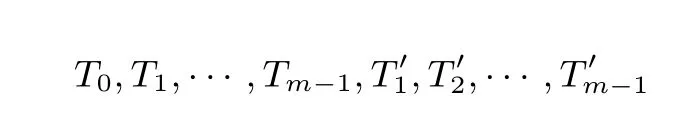
其中

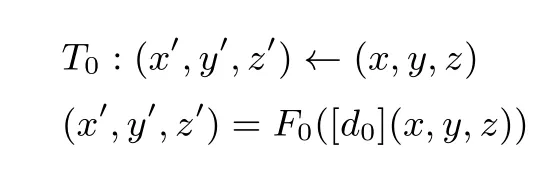
对i=1,2,··· ,m −1

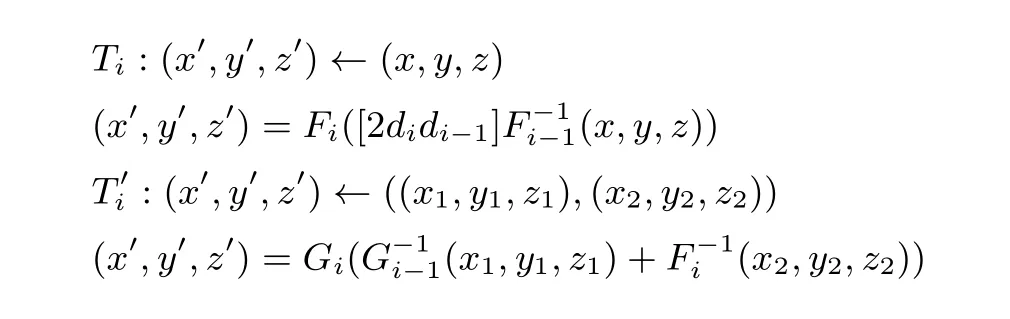
且G0=F0,Gm−1=I.

由以上分析, 我们可得倍点运算白盒初始化过程如算法3. 在初始化过程中, 输入倍数信息d, 然后将其展开成±1 表达形式, 再根据每个分量构造系列查找表, 输出查找表, 删除其它信息以完成初始化. 每个查找表的具体构造过程我们将在下一节中介绍.

算法3 Inital_WB(d)Input: d Output: d′0,T0,T1,··· ,Tm−1,T′1,T′2,··· ,T′m−1 1 {d′0,d0,d1,··· ,dm} = Expand(d);2 Gen(F0) ;3 T0 : (x′,y′,z′) = F0([d0](x,y,z));4 for i = 1 to m −1 do 5 Gen(Fi);6 Gen(Gi);7 Ti : (x′,y′,z′) =Fi([2didi−1]F−1 i−1(x,y,z));8 T′i : (x′,y′,z′) =Gi(G−1 i−1(x1,y1,z1)+F−1 i (x2,y2,z2));9 end

算法4 WB_Mul_Point(C)Input: C Output: Q 1 R0 = T0(C);2 Q′0 = R0;3 for i = 1 to m −1 do 4 Ri = Ti(Ri−1);5 Q′i = T′i(Q′i−1,Ri);6 end 7 Q = [d′0]C +Q′m−1 +[2m]C;

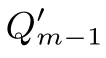
以下简要说明倍点运算白盒计算过程的正确性. 由算法3 中查找表的构造过程, 易知, 当算法4 输入点C 时, 有

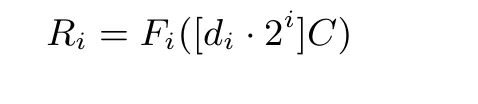
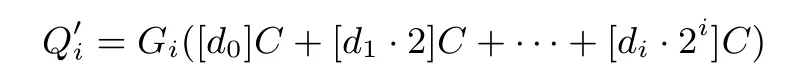
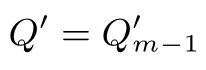
4 具体构造

4.1 查找表的构造过程

本节我们逐一介绍查找表T0,T1,··· ,Tm−1,T′1,T′2,··· ,T′m−1的构造过程.

首先考虑T0. 因[d0](x,y,z) = (x,d0·y,z), 我们只需对分量y 进行编码保护, T0的构造过程如算法5, 对输入信息(x,y,z) 查询T0的过程如算法6.

算法5 T0 =Initial_T0(d0)Input: d0 Output: T0 1 Gen(g0);2 T0 : y = g0(d0 ·x);

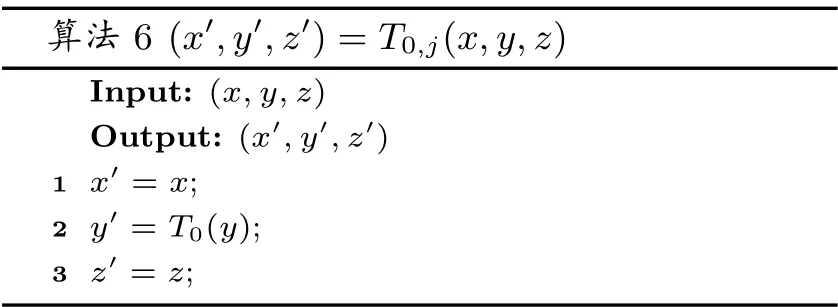
算法6 (x′,y′,z′)=T0,j(x,y,z)Input: (x,y,z)Output: (x′,y′,z′)1 x′ = x;2 y′ = T0(y);3 z′ = z;

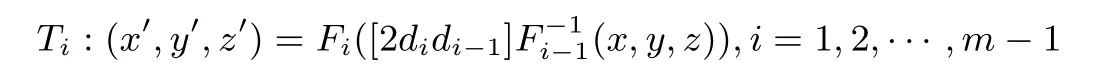
查找表

表示输入点(x1,y1,z1),(x2,y2,z2), 然后对此两点解码后的真实点作加法运算, 最后对运算结果使用随机置换Gi编码保护. 由第3 节的分析可知, 当白盒方案正常运行时, 点(x1,y1,z1),(x2,y2,z2) 解码后对应的真实点为

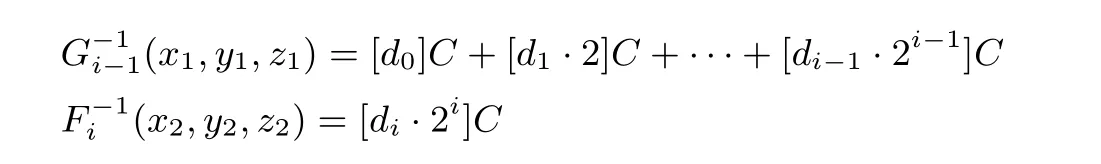
易知, 当C ̸=0 时,

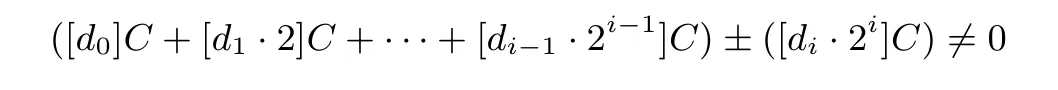
在标准射影坐标系下, 椭圆曲线上的非零点P1= (x1,y1,z1),P2= (x2,y2,z2) 的加法运算P3=(x3,y3,z3)=P1+P2̸=0 如下[21-23].

· 若P1=P2, 则

· 若P1̸=P2, 则

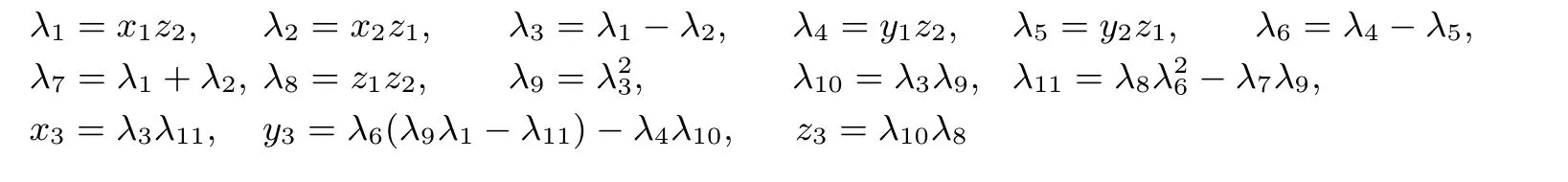
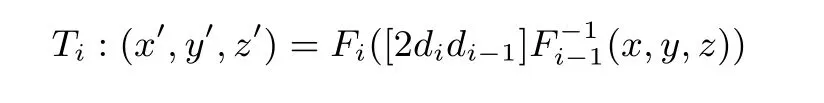
输入信息为经随机置换Fi−1编码保护后的点(x,y,z), 输出信息使用函数Fi编码保护. 记Fj(x,y,z) =(fj(x),gj(y),hj(z)),j =0,1,··· ,m −1, 则可构造以下查找表

即查找表Ti由上述系列查找表组合构成, 其中u1,u2,··· ,u6为随机置换, f0,h0为恒等置换. 当输入信息(x,y,z) 时, 查询Ti即依次查询Table1,Table2,··· ,Table9的过程如下

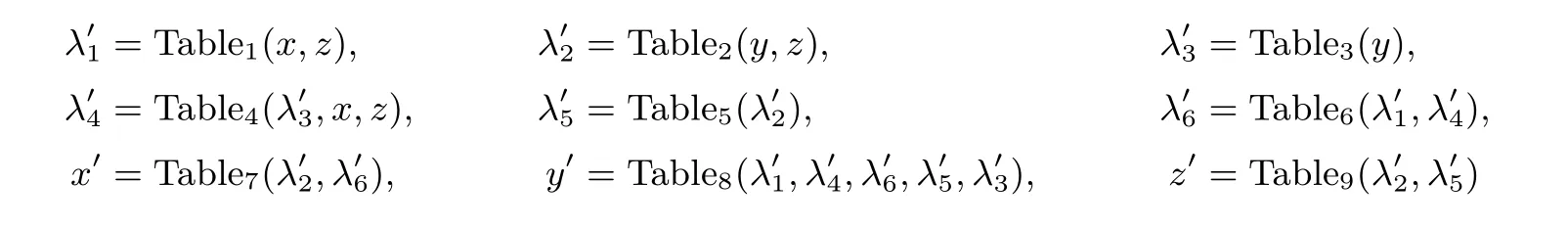
从而得到Ti的输出信息(x′,y′,z′). 由查找表T7,T8,T9的构造过程知, (x′,y′,z′) 由随机置换Fi编码保护.

4.2 余数系统与查找表的分解

由于倍点运算均在Fq上计算, 若构造查找表所选择的随机置换在Fq上选取, 查找表的规模将无法接受. 例如, 查找表Table1: y ←(x1,x2),y,x1,x2∈Fq, 若所选择的置换为Fq上的随机置换, 则查找表的规模为q2·log q 比特, 由于q 较大, 该查找表的规模难以满足实际应用. 为降低查找表的规模, 我们首先将含有多个运算的查找表进行分解, 使每个查找表只包含一种运算. 例如, 将查找表

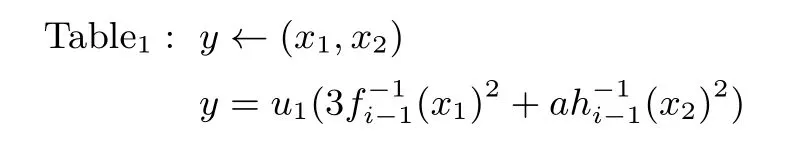
分解为

其中, v1,v2为随机生成的置换. Table1由此三个查找表组合构成, 查询Table1由依次查询此三个查找表实现. 在标准射影坐标系下, 椭圆曲线上点的加法运算只涉及模乘、模加运算, 因此对查找表进行分解后,所有查找表均可归为以下两类

分别称为模乘查找表与模加查找表, 其中, 完成平方运算的查找表可看作模乘查找表的一种特殊情况. 以下我们首先说明可以采用余数系统理论将Fq上的模乘、模加运算转化为余数系统上的运算, 从而实现对运算过程的分解, 进而实现对此两类查找表的分解.

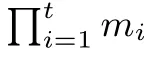
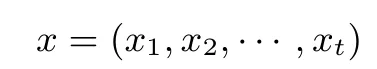
其中, x ≡ximod mi,i = 1,2,··· ,t. 对任意给定的余数表示(x1,x2,··· ,xt), 由中国剩余定理可恢复[0,M) 内的元素

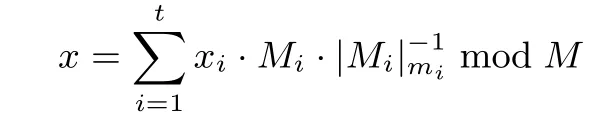
其中, Mi= M/mi,i = 1,2,··· ,t. 由余数系统的性质, 对任意x,y ∈ZM, 若x = (x1,x2,··· ,xt),y =(y1,y2,··· ,yt), 则

其中, ⊙表示模乘、模加运算. 即ZM上的模乘、模加运算可转化为余数系统上的模乘、模加运算.

余数系统下的蒙哥马利乘法[24,25],通过使用两个余数系统实现计算X·Y mod q,其中0 ≤X,Y ＜q.文献[25] 中Algorithm 1 介绍了该过程, 我们对该算法整理如下:

算法7 R=RNS_Mul(X,Y)参数设置:选取余数系统B : {m1,m2,··· ,mn}, 其中M = ∏n i=1 mi,0 ＜2q ＜M;选取余数系统B′ : {m′1,m′2,··· ,m′n′}, 其中M′ = ∏n′i=1 m′i,gcd(M,M′) = 1,M ＜M′;Input: X,Y Output: R, 满足R ≡XY M−1 mod q, 且R ＜2q 1 Q ←(−X ×B Y)×B |q|−1M ;2 将Q 在余数系统B 中的表示转换为在余数系统B′ 中的表示;3 R ←(X ×B′ Y +B′ Q×B′ q)×B′ |M|−1 M′;4 将R 在余数系统B′ 中的表示转换为在余数系统B 中的表示;5 使用中国剩余定理恢复R;

由算法7知, 我们首先输入(X,Y) 得到R = XY M−1mod q, 再次输入(R,M2) 调用该算法就可得XY mod q 的值, 即

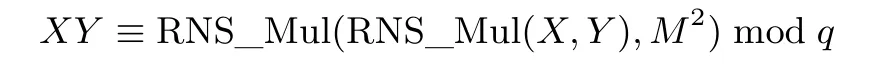
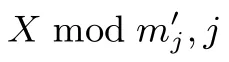
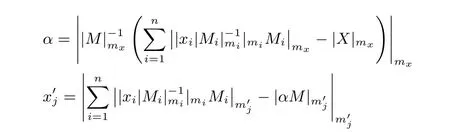
其中, mx≥n 为辅助模数. 显然, X +Y mod N 也可按类似的方式完成, 因此, Fq上的模乘、模加运算可转化为余数系统B 与余数系统B′上的运算, 据此, 我们可将模乘查找表

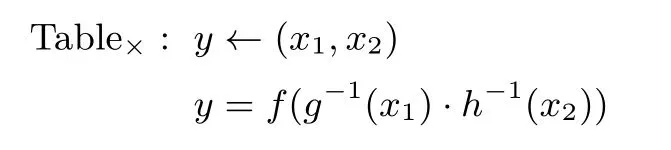
中的随机置换f,g,h 改为分别从余数系统B,B′上选取, 即

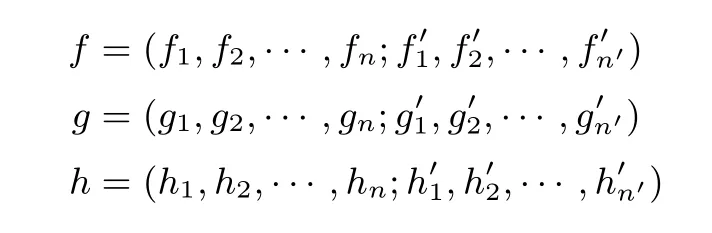
然后, 以编码保护的方式实现算法7, 即实现

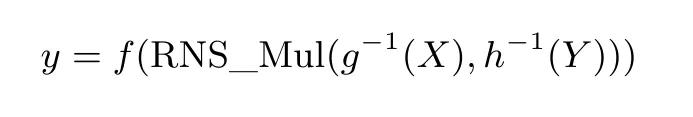
与上一节中对椭圆曲线上点的加法运算构造查找表类似, 我们将算法7 中每一步运算转换为查找表, 例如,我们将运算

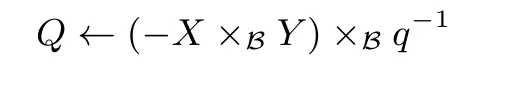
中的运算X ×BY 转化为查找表

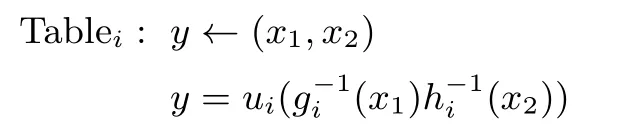
其中, i=1,2,··· ,t.

以查表的方式完成算法7 需要1 次B 中的运算, 2 次B′中的运算, 以及两个余数系统之间的转换各1 次, 构造查找表所需存储空间为

注, 我们取B 与B′规模接近, 相互转换所需存储空间相近, 常数项参与的运算可预置到存储表中.

进一步, 我们采用嵌套分解的方式, 将Fq上的元素运算转换到特定的余数系统中的运算. 给定余数系统

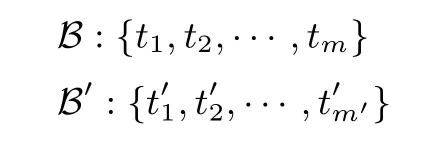
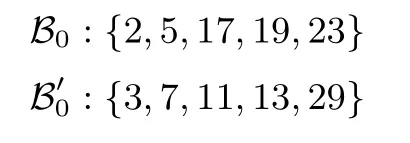
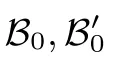
远小于未分解之前的规模.

5 安全性分析

白盒密码应用通常分为两个阶段: 初始化阶段与计算阶段. 在初始化阶段, 算法根据密钥等敏感信息,随机选取一些置换等, 生成一系列查找表或随机参数, 然后删除敏感信息, 输出这些查找表与随机参数. 该阶段涉及对敏感信息的直接处理, 需要在安全服务器、可信芯片等设备完成. 在计算阶段, 用户根据初始化结束后查找表或随机参数等, 对输入信息完成运算处理过程.

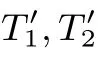
当前, 基于Chow 等白盒思想构造的AES、DES、SM4 等系列白盒方案, 均存在安全性不高等问题,主要原因在于, 这些方案受限于分组密码迭代结构, 攻击者可通过组合查找表消除一些用于保护查找表的较大规模的随机置换, 或通过仿射等价关系获取轮密钥信息, 如BGE 攻击等[8]. 本方案中, 椭圆曲线倍点运算的计算过程与分组密码迭代结构差异巨大, 我们采用一种新型的实现策略, 将所有运算均转换到较小的有限域上进行运算, 余数系统不同模数之间的关联性较弱, 攻击者即使猜测确定部分模数上的查找表所使用的编码置换, 也难以据此推出其它模数上的随机置换, 因此, 现有对基于Chow 等白盒思想的对称密码白盒方案的攻击难以直接应用到对本方案的攻击.

6 应用

6.1 SM2 解密算法白盒实现方案

SM2 密码算法是基于椭圆曲线的公钥算法, 由国家密码管理局于2010 年12 月发布, 2012 年成为我国密码行业标准GM/T 0003[21], 并于2016 年成为国家标准GB/T 32918[22]. 在SM2 解密算法中, 私钥dA只参与运算(x2,y2) = [dA]C1, 其中C1是输入的密文信息. 因此, 我们只需将SM2 解密算法中的这一运算过程采用本文所构造的倍点运算白盒实现方式实现, 即可得到SM2 解密算法白盒实现方案.

我们按算法1 将dA展开成特定的表达形式, 由于SM2 解密算法的私钥dA＜2256, 我们取m=256.此时, 由算法5 将SM2 解密算法白盒初始化后, 生成查找表

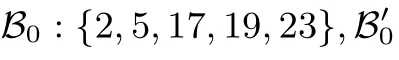
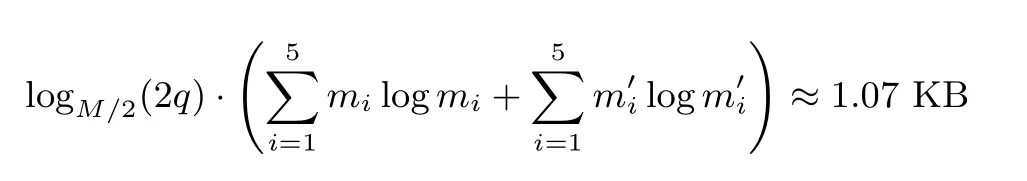
查找表Ti,i=1,2,··· ,255 的规模为

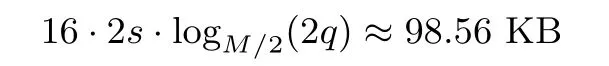
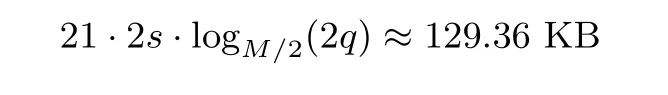
因此,基于上述余数基的SM2 倍点运算白盒实现相比于SM2 标准实现需要额外增多存储空间约为1.07+(98.56+129.36)·255 ≈56.76 MB, 完成该运算需2 次点加运算、2 次余数系统转换运算及1+255·(16+21)·(3+10)=122 656 次查表运算(注, 每次256 比特数据并行查表算作1 次查表). 我们可通过调整余数基与用于嵌套分解的余数基, 实现存储空间与查表次数之间的平衡, 以满足实际应用需求.

6.2 SM9 解密算法白盒实现方案

SM9 标识密码算法是一种基于双线性对的标识密码算法, 由国家密码管理局于2016 年3 月发布为密码行业标准GM/T 0044[23]. 对于SM9 解密算法, 私钥deB参与双线性对运算w′=e(C1,deB), 我们基于双线性对的性质, 将私钥参与的上述运算进行如下变换

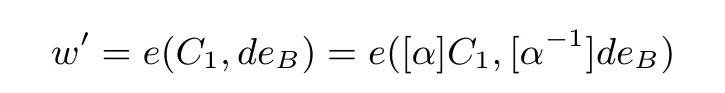
其中, α 为预先选定的随机数. 我们公开[α−1]deB, 并将[α]C1的计算过程采用本文所构造的方案白盒化实现, 即得到了SM9 解密算法的白盒实现方案, 方案所需额外的存储空间及运行效率与SM2 解密算法白盒方案相仿.

7 推广

7.1 模幂运算白盒实现

RSA 算法是目前使用最广泛的公钥密码体制之一[27]. 在RSA 解密或签名运算中, 私钥参与的运算均为模幂运算y = xdmod N. 模幂运算与倍点运算均为公钥密码算法中常见的运算, 本节将倍点运算白盒实现方法推广到模幂运算白盒实现, 并构造RSA 算法白盒实现方案.

类似地, 我们首先将模幂运算y =xdmod N 中的指数d 展开成如下形式

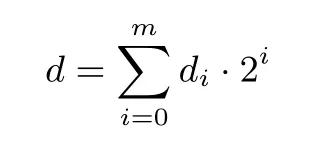
其中, d0∈{1,3,5},di∈{1,3},i=1,2,··· ,m −1,dm=1. 具体展开过程如算法8. 易知, 对任意的奇数d, 均可展开成上述表达形式. 例如, d=13=(1101)2可按算法8 展开为

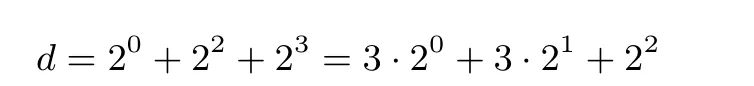
与倍点运算白盒化处理过程类似, 将模幂运算的指数按上述形式展开后, 将模幂运算进行分解, 然后采用查找表网络完成模幂运算过程. 模幂运算白盒方案初始化过程如算法9, 网络化查表计算过程如算法10, 同样的, 模幂运算白盒实现方案中的查找表可采用余数系统进行分解.

算法8 Expand(d)Input: d Output: (dm,dm−1,··· ,d0)1 设d = d′m+1d′m···d′0,d′m+1 = 1,di ∈{0,1};2 令(dm,dm−1,··· ,d1,d0) = (d′m−1 +1,··· ,d′1 +1,d′0 +2);3 tag = 1;4 for i = m to 0 do m +1,d′5 if di == 2 then 6 if tag == 1 then 7(di,di−1,··· ,d0) = (di −1,di−1 +1,··· ,d1 +1,d0 +2);8 tag = 3;end 10 else 9 11 (di,di−1,··· ,d0) = (di +1,di−1 −1,··· ,d1 −1,d0 −2);12 tag = 1;13 end 14 end 15 end

算法9 Inital_WB(d)Input: d Output: T0,T1,··· ,Tm−1,T′1,T′2,··· ,T′m−1 1 (dm,dm−1,··· ,d0) = Expand(d);2 Gen(f0) ;3 T0 : y = f0(xd0);4 for i = 1 to m −1 do 5 Gen(fi);6 Gen(f′i);7 Ti : z = fi((f−1 i−1(x))2did−1i−1);8 T′i : z = f′i(f′−1i−1(x)·f−1 i (y));9 end

8 总结

算法10 WB_Mod_Exp(x)Input: x Output: y 1 X0 = T0(x);2 Y0 = X0;3 for i = 1 to m −1 do 4 Xi = Ti(Xi−1);5 Yi = T′i(Yi−1,Xi);6 end 7 y = Ym−1 ·x2m;

公钥密码算法的运行大多依赖于较大规模的数学计算, 若简单采用传统的表格化白盒实现思路, 其存储规模远远超过实际密码系统的承受能力. 本文在研究公钥算法数学特征的基础上, 从算法底层提出了针对倍点运算、模乘运算的白盒实现策略, 可应用于SM2/9、RSA 等多种标准公钥算法. 目前公钥算法白盒化的成果很少, 希望本文的设计思路有所助益。针对具体业务场景, 我们可以通过调整实现参数, 在安全-性能-代价之间得到较好的平衡, 以此增强对此类算法的私钥保护.