喀斯特流域径流对植被和气候变化的多尺度响应
2020-07-02朱靖轩李振炜李笑含张志慧徐宪立
朱靖轩,刘 雯,*,李振炜,李笑含,张志慧,徐宪立
1 湖南师范大学资源与环境科学学院,长沙 410081 2 湖南师范大学地理空间大数据挖掘与应用湖南省重点实验室,长沙 410081 3 中国科学院亚热带农业生态研究所,长沙 410125
径流是人类生产生活用水的主要来源之一,对径流的研究是对水资源进行有效开发利用和管理的基础[1]。过去几十年中,全球气候变化促使水循环加快,改变了降水的时空变化,极端水文事件发生更加频繁[2- 3],导致我国南方地区的洪涝灾害在不断增加,水生态环境在不断恶化[4- 6]。喀斯特地区在全球分布十分广泛,约占地球陆地面积的7%—12%,供应了全球约25%人口的水源[7]。我国是全球喀斯特面积最大、分布最为广泛的国家之一,尤其是在西南地区,喀斯特连片分布面积多达54万km2[7- 8]。由于碳酸盐岩的广泛分布,喀斯特地貌具有土层浅薄、土壤入渗能力强和地形复杂等特点[9- 10]。因此,喀斯特地表持水能力较弱,水资源有效利用较为困难;同时,喀斯特地区局部地下管网通畅性差,极易发生洪涝灾害。喀斯特地区旱涝频发,严重限制了当地社会经济可持续发展。因此,研究喀斯特流域径流变化特征,以及其对气候和植被变化的响应,对合理配置喀斯特流域水资源,促进流域社会经济和生态环境保护可持续发展,具有十分重要的现实意义。
径流的变化规律错综复杂,其具有非线性、随机性和突变性等复杂特点,主导了自然界中整个水文系统的变化[11]。其受到了气候、植被、土壤、地形和人类活动的共同影响,其中植被和气候变化是引起径流变化的重要因素[12]。植被通过地上部分的林冠截留对降水进行再分配,以及通过地表枯落物和地下根系增加土壤的入渗能力等改变径流的产生机制[13- 14]。归一化植被指数(Normalized Difference Vegetation Index,NDVI)与植被覆盖度、生长状况、生物量和光合作用强度有着密切的关系,被广泛应用于植被动态监测[15]。已有研究表明,在年内变化上,NDVI与径流呈显著正相关,但年际变化上,关系相对复杂,不具有明显相关性[16]。气候因素包括降水、潜在蒸散发以及气温等,降水是引起径流变化最敏感的因子[17]。气候变化直接导致降水的空间分布、时间变异以及地表蒸发等的变化来影响流域的径流量[18- 19]。流域径流与气象要素相关性研究表明,径流下降的主要原因是人类活动引起了流域内蒸发量增加,而且导致径流对降水的响应程度下降[20]。很多学者仍采用线性趋势法、Man-Kendall趋势检验、滑动平均和多元回归分析等方法研究气候水文变化趋势[21- 24]。然而,气候和水文系统是一个复杂的非线性系统[25],这些因子的长期变化过程大多数是非线性、非平稳的变化过程,而且通常伴随着多尺度或者周期性振荡。所以,线性方法并不能准确地揭示出植被、气候和水文系统的非线性特征。因此,一些研究者采用了小波分析和集合经验模态分解等非线性方法。柏玲等[6]利用集合经验模态分解方法对开都河长时间径流序列进行了多尺度分析;董喆等[26]利用小波分析方法研究了在不同周期下,降水与植被对径流的调节作用;吴创收等[27]通过小波分解方法,揭示了珠江流域径流周期变化特征,同时得出径流的变化周期与降水的变化周期具有较好的相关性。但是,集合经验模态的参数设置没有特定的方法和规则,针对不同的信号缺乏自适应性,且应用于多元数据分析时存在分解的本征模函数的数量不一致问题。小波分析虽然具有时频分辨功能,但是其作用的对象是单一序列的,只能反映不同时频域上的径流变化规律,无法反映植被和气候因素对径流的影响[20]。同时,小波分解的小波基和分解层的数量需要人为的设定,自适应性较差[6],使得其在水文领域的应用具有一定的局限性。
随着信号检测手段的不断进步,有关于信号处理的方法在不断出现。多元经验模态分解(multivariate empirical mode decomposition,MEMD)是一种与小波分析相对应的另外一种多尺度分析方法,是经验模态分解(Empirical Mode Decomposition,EMD)在多元空间上的扩展[28]。它可以依据数据自身的尺度特征,经验性地将多元数据分解成多个表征尺度,有效解决了线性和平稳性假设的问题[28]。EMD和EEMD在处理多元数据时,存在分解的本征模函数的数量不一致问题,而MEMD可以将多元数据分解成具有相同个数的多元本征模函数分量。虽然 MEMD方法具有很多明显的优点,但是在地质结构背景复杂的喀斯特地区径流研究中尚未得到应用。因此,本文利用MEMD方法,基于1982—2015年植被、气象和水文数据,分析喀斯特流域径流及其影响因子的非线性变化特征,研究径流在不同时间尺度对这些因子的响应,进而揭示径流对植被、气象因子变化的响应过程,并对径流深进行预测,为喀斯特流域复杂地质背景下径流相关研究提供帮助。
1 研究区概况
西江是华南地区最长河流,发源于云南省曲靖市乌蒙山余脉马雄山的东麓,先后流经云南、贵州、广西和广东等省份(图1)。西江全长2214 km,流域(21°36′17″—27°00′21″N, 102°16′52″—113°23′51″E)总面积约为3.53×105km2,地形以高原、山地和平原为主,最低和最高海拔为2 m和2888 m,西部海拔高于东部。气候为典型的亚热带和热带季风湿润气候,多年平均气温约为18 ℃,多年平均降水量约为1470 mm,主要集中在每年的5月至10月份,流域的降水由东南向西北逐渐减少。土地利用以林地为主,约占流域面积的62%。流域内喀斯特地貌分布较为广泛,约占流域面积的45%。研究区内选择郁江、红水河、浔江和梧州4个典型喀斯特流域(图1),其喀斯特地貌面积占比分别为42%、64%、51%和47%。

图1 研究区域位置图Fig.1 Location map of research area
2 数据与方法
2.1 数据来源与处理
(1)径流数据:1982—2015年西江流域4个水文站(南宁、迁江、大湟江口、梧州)的年径流数据,来自水利部编制的水文年鉴。
(2)NDVI数据:采用1982—2015年GIMMS NDVI数据,该数据是由美国国家航天航空局(NASA)推出的全球植被变化数据。时间分辨率为15d,空间分辨率为8 km×8 km[29]。利用最大值合成法(Maximum Value Composite,MVC)生成年NDVI最大值,可以有效地减少因为云、阴影、气溶胶、太阳高度角及视角等带来的影响[30]。
(3)1982—2015年西江流域36个气象站的降水、气温等数据。来自中国气象科学数据共享服务网。通过空间插值方法获得流域面气象数据。此外,1982—2015年的潜在蒸散发数据是根据研究区内气象站点的观测资料数据,利用联合国粮农组织修正的Penman-Monteith公式[31]计算得到。
2.2 研究方法
2.2.1Mann-Kendall趋势检验
Mann-Kendall 趋势检验是研究水文变化趋势研究的良好方法[32- 33],其主要的原理如下:
(1)
其中:
(2)

(3)
(4)
式中,Xi代表第i年的数值,Xj代表第j年的数值。当i
2.2.2MEMD
MEMD是对标准经验模态分解(Empirical mode decomposition,EMD)的多元扩展,是通过多维空间超球面的方向向量求均值包络,从而实现不同频率尺度下不同变量的共同模式分解[28,34]。自然界中的各种事物的整体变化受到不同过程影响,而且在不同尺度下以不同的强度发生[35]。在同一个尺度下发生的过程可以分解成为相同的本征模函数(Intrinsic mode function,IMF)。每个变量分解出的本征模函数(IMF)数量相同,每层的IMF频率相同,IMF频率高低由分解的次序所决定,先分解的频率高,后分解的频率低。不同变量对应的IMF按尺度对齐,组成多元IMF。

(1)获取n维空间向量集X;
(2)计算时间序列V(s)沿着给定方向Xθk的投影pθk(s);
(5)利用以下公式计算包络线的均值M(s);
(5)
(6)通过D(s)=V(s)-M(s)得到本征模函数D(s)。假如D(s)满足多元IMF的判断标准,则将D(s)=V(s)-M(s)的结果作为步骤(2)的输入变量。如果不满足,则将D(s)作为步骤(2)的输入变量,继续进行迭代运算。
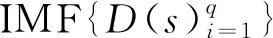
3 结果与分析
3.1 径流深及其影响因子的变化趋势
4个流域中,年均径流深最小的为红水河流域,最大的为梧州流域(表1)。4个流域间年均NDVI、降水量、潜在蒸散发和气温之间差异均较小。流域的径流深和降水量的变异系数均呈中等程度变异(10% < Cv < 100%),而NDVI、潜在蒸散发和气温均呈弱变异(Cv < 10%)。在4个流域中,径流深与降雨量呈显著正相关(P<0.01),与潜在蒸散发呈显著负相关(P<0.01),而与NDVI和气温无显著相关性(P>0.05)(图2)。

表1 径流深及其影响因子平均值及变化趋势
NDVI: Normalized Difference Vegetation Index

图2 径流深及其影响因子相关性矩阵图Fig.2 Correlative Matrix plot of runoff and its influencing factorsRF:径流深 Runoff;NDVI:归一化植被指数Normalized difference vegetation index;PRE:降水 Precipitation;PT:潜在蒸散发 Potential evaporation; T:气温 Temperature; R:相关系数Correlation coefficient;P:显著性水平 Significance level
通过Mann-Kendall趋势检验,发现流域的NDVI和气温均表现为显著增加的趋势(P<0.05;表1)。流域的径流深和降水均表现为下降的趋势,但只有红水河流域的径流深通过了0.05信度检验。流域的潜在蒸散发均表现为增加趋势,但仅郁江流域通过了0.05信度检验,呈显著增加趋势,其余流域增加趋势不显著。
3.2 径流深及其影响因子的多尺度关系
利用MEMD方法将4个流域的径流深及其影响因子的多元数据分解成4个本征模函数IMF和1个残差(图3)。与EMD方法相似,各变量的震荡周期随着IMF增大而增大。对于一组经过分解的多元数据,在相同IMF中,不同的变量通常具有相同的震荡数量,所以具有相似的震荡频率[36]。本文使用Hilbert 变换来计算不同IMF之间的瞬时频率,得到不同的尺度。

图3 基于多元经验模态分解的径流深及其影响因子的本征模函数和残差Fig.3 Intrinsic mode function (IMF) and residues of runoff and its influencing factors based on multivariate empirical mode decomposition
每个流域不同因子的IMF对应的时间尺度的平均值代表该IMF对应的特征尺度(表2)。郁江流域IMF1、IMF2、IMF3和IMF4对应的特征尺度为2.9、5.0、8.7、19.5年;红水河流域IMF1、IMF2、IMF3和IMF4对应的特征尺度为3.1、5.0、9.6、22.4年;浔江流域IMF1、IMF2、IMF3和IMF4对应的特征尺度为3.0、5.6、10.0、21.5年;梧州流域IMF1、IMF2、IMF3和IMF4对应的特征尺度为3.0、5.4、10.0、22.4年。除郁江流域外,其他3个流域各因子的IMF4所对应尺度的变异系数较大,表明该尺度下无可以代表径流深与其影响因子的共同尺度。4个流域中,4个本征模函数IMF对应的平均时间尺度比较接近,而且径流深的尺度也比较相似,该结果表明控制径流的过程发生在相似的尺度。

表2 径流深及其影响因子本征模函数(IMF)的尺度
IMF:本征模函数 Intrinsic mode function;括号中的数字代表径流深及其影响因子本征模函数所对应尺度的变异系数(%)
各流域径流深及其影响因子的IMF所表征的尺度方差贡献率不同(表3)。郁江流域径流深方差贡献率主要分布在IMF1和IMF2处(32%和36%),所对应尺度为3年和5年。红水河流域径流深方差贡献率主要分布在IMF3和IMF4处(26%和28%),对应的尺度约为10年和22年。浔江和梧州流域径流深方差贡献率主要分布在IMF1和IMF4处(35%和31%、36%和34%),对应尺度约为3年和22年。从其余影响因子的IMF方差贡献率可以看出,NDVI除了红水河流域主要分布在IMF1和IMF4处,且其残差值较小(2.4%),其余流域主要分布在IMF1和IMF4及残差部分。郁江和红水河流域降水的主要表征尺度分别分布在IMF1和 IMF2、IMF1和IMF3处(43%和21%、51%和16%),浔江、梧州流域主要分布在IMF1和IMF4处(50.1%和18.6%、50.6%和20.4%)。郁江和红水河流域的潜在蒸散发的表征尺度主要分布在IMF1和IMF2处,对应的特征尺度约为3年和5年;浔江和梧州流域主要分布在IMF1和IMF4处,对应的特征尺度约为3年和22年。4个流域的气温表征尺度主要在IMF1和IMF2处,即主要分布在年际尺度上。
径流深及其影响因子多尺度相关性如图4所示。每个流域降水量和潜在蒸散发与径流深的多尺度关系最显著,在所有表征尺度均呈显著相关。径流深与NDVI和气温在一个表征尺度上呈显著正或负相关,而在另外一个尺度上呈显著负或正相关。这主要是因为在一个表征尺度上呈现正或负相关,会降低在另外一个表征尺度上的负或正相关程度,同时导致了径流深与NDVI和气温在年尺度上相关性不显著。在郁江流域,NDVI与径流的相关性主要表现在IMF1、IMF2、IMF4和残差处;红水河流域为IMF1、IMF3、IMF4和残差;浔江流域为IMF2、IMF3、IMF4和残差;梧州流域为IMF2、IMF4和残差。郁江流域的气温与径流深的相关性主要体现在IMF3、IMF4和残差处,其余流域主要体现在IMF3和残差处。一般情况下,随着表征尺度的增大,径流与其影响因子之间的相关性有增大的趋势,即这些因子对径流深的影响程度有增大趋势。除此之外,在残差部分,径流深与其影响因子均存在显著相关性(P<0.05),这在一定程度上表明这些影响因子与径流深之间存在一定关联。径流深与NDVI和气温在年尺度上不存在显著相关性,但是径流深与两者通过MEMD分解,在某些表征尺度上呈显著相关,这说明了研究径流深与其影响因子的时间序列多尺度关系可以获得更多的信息。
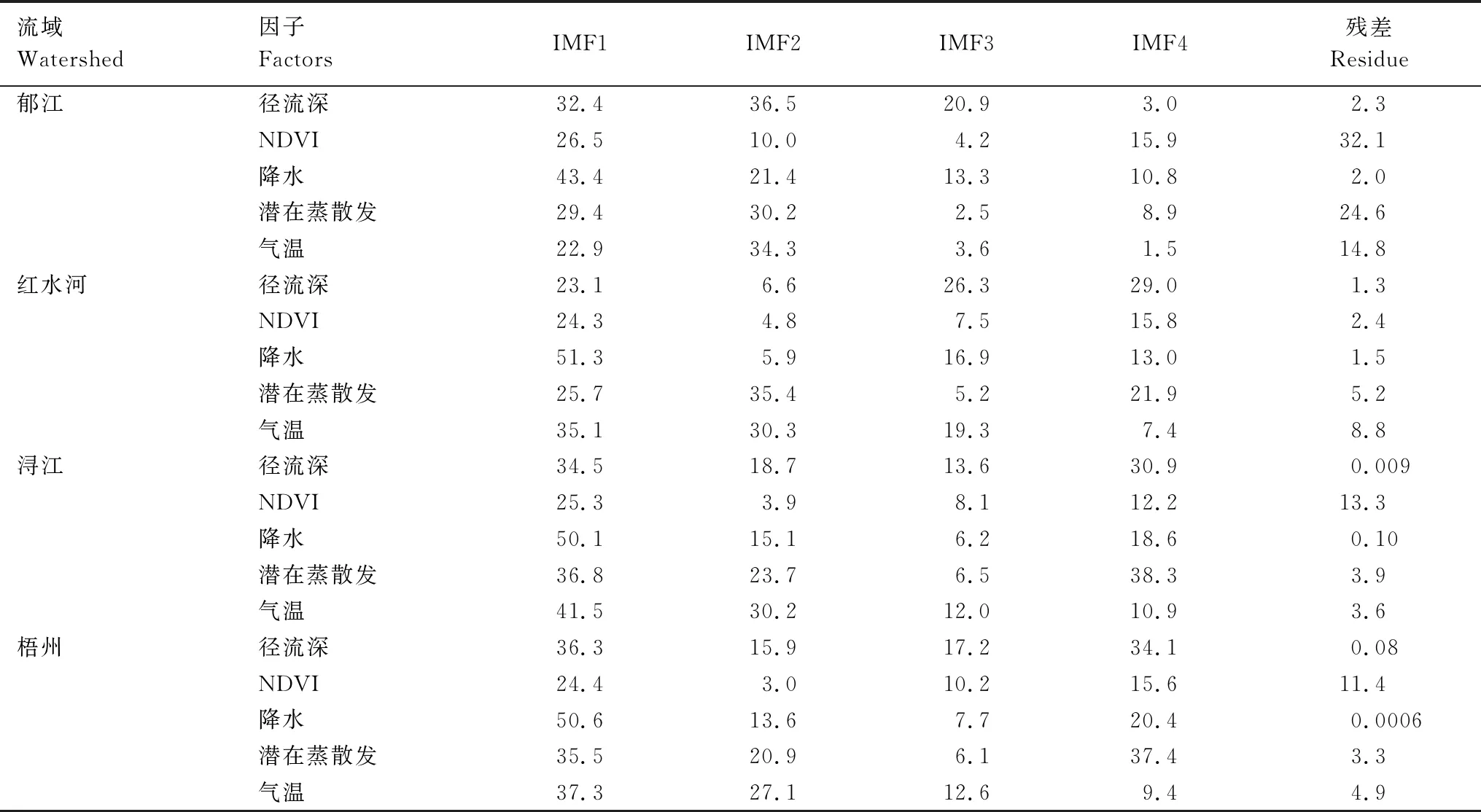
表3 径流深及其影响因子的本征模函数(IMF)和残差占原始数据方差的百分比

图4 基于多元经验模态分解的各本征模函数(IMF)和残差的径流深与其影响因子的相关性分析图Table 4 Figure of correlation coefficients between runoff and its influencing factors for each Intrinsic mode function (IMF) and residue based on multivariate empirical mode decompositionNDVI:归一化植被指数Normalized difference vegetation index;PRE:降水 Precipitation;PT:潜在蒸散发 Potential evaporation;T:气温 Temperature;**表示显著性水平小于0.01;*表示显著性水平小于0.05
此外,利用MEMD方法进行数据分解有两点值得注意。第一,一些变量的残差部分的方差贡献率较大,比如郁江流域的NDVI,残差部分的方差贡献率为32.1%,这可能是因为研究时段较短,更大的表征尺度未被发现;第二,每个变量的方差贡献率相加之和不等于100%,主要是因为每个特征尺度下的生态过程不是独立的,变量的不同IMF缺少完全正交性[36]。
3.3 基于MEMD的径流深预测
利用多元回归模型可以得到每个IMF径流深的预测模型(表4)。从表中可以看出,这些预测模型的可调整R2的范围在0.67到1之间,而且一般随着IMF增大而增大。可以确定,表征尺度越大,对径流深的预测精度越高,并且模型中所选因子对径流深的影响程度更大。基于所有IMF和残差的径流深预测结果,利用多元逐步回归方法进行径流深预测。4个流域径流深预测值和实测值的R2,RMSE,NSE和1∶1线均优于直接利用多元逐步回归拟合的结果(表5;图5)。由此可见,利用MEMD方法对径流深的预测精度要高于利用原始数据直接进行多元逐步回归预测的结果。这进一步说明了在原始时间序列上的简单分析难以解释NDVI、温度与径流之间关系的复杂性。
表4 基于多元模态分解的每个本征模函数和残差的径流深多元逐步回归预测模型及回归统计特征(可调整R2和F值)
Table 4 Predictive modeling and regression statistics (F-value and adjustedR2) for runoff for each intrinsic mode function and residue using stepwise multiple linear regression based on multivariate empirical mode decomposition

流域WatershedIMF公式FunctionR2F郁江IMF1-3.587+0.581(0.801)PRE-74.669(-0.235)T-13.443(-0.201)NDVI0.7941.79IMF2-6.785+0.63(0.575)PRE-2.888(-0.816)PT+159.869(0.581)T0.8773.34IMF33.104+0.601(0.57)PRE-302.788(-0.471)T0.88122.04IMF4-2.091+0.386(0.871)PRE+247.387(0.661)T+13.458(0.513)ND-VI0.92126.74残差951.909-1.309(-1.345)PT+67.625(0.65)T-4.882(-0.305)ND-VI1.0756358原始数据-363.473+0.702(0.836)PRE0.6974.23红水河IMF1-0.13+0.289(0.614)PRE-1.063(-0.398)PT+40.846(0.219)T0.8251.58IMF20.142+0.604(0.815)PRE-22.39(-0.209)T0.7448.34IMF31.4+0.669(0.766)PRE-64.934(-0.242)T0.6735.04IMF4-0.398+0.593(0.568)PRE-1.589(-0.491)PT+85.17(0.187)T1.02393.07残差2228.644-1.914(-1.35)PT+3.889(0.35)NDVI1.02927483原始数据575.359+0.509(0.726)PRE-0.653(-0.232)PT0.7345.00浔江IMF10.573+0.543(0.847)PRE0.7180.93IMF2-0.219+0.676(0.783)PRE+30.041(0.249)NDVI0.8593.73IMF32.009+0.632(0.55)PRE-1.711(-0.376)PT+17.616(0.245)NDVI0.90103.72IMF4-2.934+0.993(0.992)PRE0.981880.85残差-2140.752+1.479(6.295)PRE+0.813(5.441)PT1.0106793原始数据-273.478+0.688(0.885)PRE0.78115.66梧州IMF1-0.717+0.574(0.845)PRE0.7179.79IMF2-1.885+0.624(0.719)PRE+42.341(0.3)NDVI+40.873(0.192)T0.8044.10IMF30.871+1.05(0.874)PRE-0.804(-0.146)PT0.94257.17IMF4-0.92+1.09(1.051)PRE+0.19(0.061)PT1.06412残差-1320.21+32.976(0.92)T+1.052(0.112)P1.0613063296原始数据-287.998+0.711(0.887)PRE0.78117.66
NDVI:归一化植被指数Normalized difference vegetation index;PRE:降水 Precipitation;PT:潜在蒸散发Potential evaporation;T:气温 Temperature;括号中的数字代表标准偏回归系数

表5 多元模态分解与多元逐步回归预测径流深效果
R2:决定系数 Coefficient of determination;RMSE:均方根误差 Root mean squared error;NSE:纳什效率系数 Nash-Sutcliffe efficiency coefficient

图5 多元经验模态分解前后多元逐步回归预测径流与实际径流对比Fig.5 Observed vs. estimated runoff using stepwise multiple linear regression models before and after multivariate empirical mode decomposition

图6 径流深预测值与单个本征模函数或残差处预测值的决定系数Fig.6 Coefficient of determination between runoff predicted value and predicted IMFs (residue)
径流深的预测值与每个IMF或者残差处的预测值的决定系数如图6所示。从该图中可以看出每个IMF和残差对于径流深预测值的重要性程度。郁江流域主要贡献者为IMF2;红水河、浔江和梧州流域主要贡献者为IMF4。即郁江流域的年际尺度上对径流预测起主要作用,而红水河、浔江和梧州流域的年代际尺度上对径流预测起主要作用。
4 讨论
多元经验模态分解量化了流域径流深与植被和气候因子在不同尺度上的相关性,可以从复杂的角度初步理解喀斯特流域径流与其影响因子的内在作用机制,加深对此区域径流变化以及驱动因子的研究。运用传统的线性分析方法,无法揭示径流与其影响因子在不同尺度上的相关性,所以,以往的研究中,有些学者运用了小波分析和集合经验模态分解(EEMD)等方法。李宝富等[37]运用了EEMD方法研究了沂河流域径流对气候变化的响应,得出了在不同尺度上气候因子对于径流的影响机制存在明显不同,在较大尺度上往往与径流的关系更加密切。凌红波等[38]通过小波分析方法,揭示了天山地区径流和气象因子之间存在明显的多时间尺度相关关系。这些研究与本文研究结果较为一致,为区域水资源合理利用提供了重要的理论支撑。
径流深与降水和潜在蒸散发在不同的时间尺度始终呈显著相关(P<0.05),而与NDVI和气温在某些尺度上并不显著。说明与降水和潜在蒸散相比,气温和植被对于径流的影响机制相对复杂。在短时间尺度内,气温主要通过影响蒸散发等因素间接影响径流的变化。对于降水补给型河流来说,径流主要受到降水量的影响,气温的影响较小。但在较长的时间尺度上,气温变化会对气候系统产生长期影响,进而通过影响降水的时空分配格局引起流域径流变化。植被对于径流影响机制存在复杂性,主要原因是植被一方面可以减少表面径流,提高蒸散发;另一方面,气温和降水可以通过影响植被覆盖间接影响径流[39]。喀斯特流域由于复杂的双层水文地质结构,可能更加剧了上述影响机制的复杂性。
从预测的效果来看,经过多元模态分解后的数据进行径流预测精度高于原始数据直接预测径流深,主要原因在于多元经验模态方法在某些特征尺度上可以获得相关因子对径流的影响程度。该方法在土壤水分含量[36,40]预测上取得较好的效果。由于多元经验模态分解的理论基础建立时间相对较短,所以在径流领域的应用并不多见。
5 结论
本文主要分析了4个喀斯特流域径流及其影响因子1982—2015年的变化趋势,以及径流对这些因子变化的多尺度响应。主要结论如下:
(1)通过Mann-Kendall趋势检验方法,表明4个流域的气温和NDVI均呈显著增加的趋势;除红水河流域的径流深呈显著下降趋势外,其余流域的下降趋势并不显著;同时4个流域降水的下降趋势也不显著。
(2)利用MEMD将4个流域的径流深及其影响因子的多元数据分解成4个本征模函数IMF和1个残差,发现郁江流域径流深方差贡献率主要分布在3年和5年尺度上;而红水河流域径流深方差贡献率主要分布在10年和22年尺度上;浔江和梧州流域径流深方差贡献率主要分布在3年和22年尺度上。
(3)径流深与其影响因子在不同时间尺度上的相关性与原始数据相关性不同,随着尺度的不同而存在差异性。在不同尺度下,4个流域降水量和潜在蒸散发均与径流深之间存在显著相关性,而与NDVI和气温在原始时间序列上不存在显著相关性,但是其与两者的时间多尺度关系在某些表征尺度上存在显著相关性。
(4)利用MEMD方法对径流深进行预测,发现4个流域径流深的预测精度均优于直接利用多元逐步回归拟合的结果,因此该方法可用于西南喀斯特区径流量的预测。
