Hilbert空间上投影算子的Birkhoff-James正交性

李珊珊， 孟 庆

(曲阜师范大学 数学科学学院, 山东 曲阜 273165)

1 引言与预备知识

Hilbert空间与Banach空间的主要区别在于Hilbert空间中有几何结构,这种几何结构使我们对Hilbert空间有了更清晰的认识.由于缺少相应的几何结构,Banach空间的结构就显得十分复杂.为研究Banach空间的结构,很多学者在Banach空间中建立几何结构,其核心概念是向量的正交性.其中最引人注目的是Birkhoff-James正交性[1].近年来,Birkhoff-James正交性引起了部分学者的关注,并取得了一系列重要的研究成果[1-6].本文主要讨论有限维Hilbert空间上投影算子的Birkhoff-James正交性.

本研究需要以下定义:

定义1[1，5]设X为复赋范线性空间,x,y∈X.

(1) 若对任意λ∈,有‖x+λy‖≥‖x‖,则称x与yBirkhoff-James正交,记为x⊥By；

(2) 若对任意λ∈{0},有‖x+λy‖>‖x‖,则称x与y强Birkhoff-James正交, 记为

定义2[7]设A是有单位的巴拿赫代数,a∈A.集合σ(a)={α∈C|a-α是不可逆的}称为a的谱,r(a)=sup{|α|∶α∈σ(a)}称为a的谱半径.

定理2[9]设V是C*-代数A上的HilbertC*-模.若x,y∈V,则x⊥By的充要条件是存在φ∈S(A),使得φ(〈x,x〉)=‖x‖2,φ(〈x,y〉)=0.

设H为Hilbert空间,Y1,Y2为H的闭子空间,P,Q分别为H到Y1,Y2的投影算子.若Y1与Y2正交,则称投影P与Q正交,记为P⊥Q.

定理3 设P,Q为Hilbert空间H上的投影算子,则以下论述等价:

(1)P⊥Q;

(2)PQ=0;

(3)P≤I-Q,即P是I-Q的子投影;

(4)PH⊂(QH)⊥;

(5)QH⊂(PH)⊥.

2 主要结果

由定理1,容易证明以下定理:

‖Pξ‖=‖P‖=1,〈Pξ,Qξ〉=0(QPξ=0).

以下定理从值域的角度刻画投影算子的Birkhoff-James正交性.

定理5 设P,Q为有限维Hilbert空间H上的非零投影算子,则P⊥BQ的充要条件是PH∩(QH)⊥≠{0}.

证明(a)必要性. 因为P⊥BQ,所以由定理4可知，存在单位向量ξ∈H,使得

‖Pξ‖=‖P‖=1,〈Pξ,Qξ〉=0.

由于ξ=Pξ+(I-P)ξ,故

1=‖ξ‖2=‖Pξ‖2+‖(I-P)ξ‖2.

因为‖Pξ‖2=‖P‖2=1，所以‖(I-P)ξ‖2=0,从而有Pξ=ξ.又因为

0=〈Pξ,Qξ〉=〈ξ,Qξ〉=〈ξ,Q2ξ〉=〈Qξ,Qξ〉=‖Qξ‖2.

所以Qξ=0,从而存在单位向量ξ∈PH∩(QH)⊥.因此PH∩(QH)⊥≠{0}.

(b)充分性. 因为PH∩(QH)⊥≠{0}，所以存在单位向量ξ∈H,使得Pξ=ξ,Qξ=0.又因为

‖Pξ‖=‖ξ‖=1=‖P‖,〈Pξ,Qξ〉=0，

所以有P⊥BQ.

根据上述结果可得推论1.

推论1 设P,Q为有限维Hilbert空间H上的非零投影算子,则以下论述等价:

(1)P⊥BQ;

(2)PH∩(QH)⊥≠{0};

(3)PH∩kerQ≠{0};

(4)PH∩(I-Q)H≠0;

(5)P∧(I-Q)≠0.

证明由于(QH)⊥=(I-Q)H=kerQ,故根据定理5知(1)(2)(3)(4)是等价的.因为投影P∧(I-Q)的值域为PH∩(I-Q)H,所以(4)与(5)等价.

证明必要性显然.

下面证充分性.

因为P⊥BQ,所以由定理5可知存在单位向量ξ∈H,使得Pξ=ξ，Qξ=0.又因为

‖Pξ‖=‖ξ‖=1=‖P‖,Qξ=0，

注当P是零投影算子、Q是任意非零投影算子时,定理6的结论仍成立;当Q是零投影算子、P是任意非零投影算子时,定理6的结论不成立.

定理7 设P,Q为有限维Hilbert空间H上的非零投影算子.若dim(I-Q)=1,则以下论述等价:

(1)P⊥BQ;

(2)I-Q⊥I-P;

(3) (I-Q)⊥B(I-P).

证明

(1)⟹(2)由于P⊥BQ，故根据推论1的(4)可知PH∩(I-Q)H≠{0}.因为dim(I-Q)=1,所以PH∩(I-Q)H=(I-Q)H,从而(I-Q)H⊂PH,进而I-Q≤P.因为I-Q≤P,所以(I-Q)P=I-Q,从而(I-Q)(I-P)=0.因此由定理3可知I-Q⊥I-P.

(2)⟹(3)因为I-Q⊥I-P,所以根据定理3可知I-Q是P的子投影,从而P∧(I-Q)≠0.因此由推论1可知(I-Q)⊥B(I-P).

(3)⟹(1)因为(I-Q)⊥B(I-P),所以根据推论1的(4)可知(I-Q)H∩PH≠{0},从而P⊥BQ.

定理8 设P,Q为有限维Hilbert空间H上的非零投影算子.若dimP=1,则P⊥BQ的充要条件是P⊥Q.

证明(a)必要性. 由于P⊥BQ,故根据推论1的(4)可知PH∩(I-Q)H≠{0}.因为dimP=1,所以PH∩(I-Q)H=PH,从而PH⊂(I-Q)H,进而P≤I-Q.因为P≤I-Q，所以P(I-Q)=P,从而PQ=0.因此由定理3可知P⊥Q.

(b)充分性. 由于P⊥Q,故根据定理3可知P是I-Q的子投影.因为P也是P的子投影,所以P∧(I-Q)≠0.因此由推论1的(5)可知P⊥BQ.

注当dimP=2时,定理8的结论不成立.下面举例说明.

例设H为三维Hilbert空间,{e1,e2,e3}为一组标准正交基,P,Q为H上的非零投影算子.因为P(H)=span{e1,e3},Q(H)=span{e2,e3},所以

(I-P)(H)=span{e2}, (I-Q)(H)=span{e1}.

从而

P(H)∩(I-Q)(H)=span{e1}≠{0},

Q(H)∩(I-P)(H)=span{e2}≠{0}.

由此可得P⊥BQ且Q⊥BP.又因为P(H)∩Q(H)=span{e3},所以PQ≠0,从而P⊥Q不成立.

定理9 设P为有单位元的C*-代数A中的非零投影,则P⊥BI不成立.

证明用反证法.设P⊥BI,则对任意的λ∈,‖P+λ‖≥‖P‖=1.等价于对任意的λ∈,有:

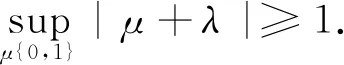
也等价于对任意的λ∈,max{|λ|,|1+λ|}≥1.若取则有：

因此P⊥BI不成立.

对于两个交换的投影, 有以下结论：

定理10 设P，Q为有限维Hilbert空间H上的非零投影算子.若PQ=QP,则以下论述等价:

(1)P⊥BQ；

(2)P(I-Q)≠0；

(3)P∧(I-Q)≠0；

(4)P≠PQ；

(5)P不是Q的子投影.

证明

(1)⟹(2)用反证法.因为P(I-Q)=0,所以P=PQ,从而P≤Q. 在C*-代数A上,非零投影P≤Q.设B=QAQ,则B也是C*-代数,且B的单位元为Q,P∈B.因此根据定理9可知P⊥BQ不成立.

(2)⟹(3)由于PQ=QP,故有P∧Q=PQ.因为P(I-Q)≠0,所以P∧(I-Q)≠0.

(3)⟹(4)由于PQ=QP,故有P∧Q=PQ.因为P∧(I-Q)≠0,所以P(I-Q)≠0，从而P-PQ≠0，进而P≠PQ.

(4)⟹(5)用反证法.因为P是Q的子投影,所以P≤Q,从而P=PQ.由于P≠PQ,故P不是Q的子投影.

(5)⟹(1)用反证法.因为P⊥BQ不成立,所以P(I-Q)=0,从而P=PQ,进而P≤Q.因此P是Q的子投影.由于与条件矛盾,故有P⊥BQ成立.

由以上讨论可知，当P⊥BQ时,一般得不到P⊥Q,因此P+Q不一定是投影.但我们可以考查矩阵代数,且有以下结论：

定理11 设P1，P2，Q1，Q2为有限维Hilbert空间H上的非零投影算子.若P1⊥BQ1,P2⊥BQ2,则有：

证明因为P1⊥BQ1,所以存在φ1∈S(H),使得

φ1(P1)=‖P1‖2=1，φ1(P1Q1)=0.

因为P2⊥BQ2,所以存在φ2∈S(H),使得

φ2(P2)=‖P2‖2=1，φ2(P2Q2)=0.

又因为

所以有：

从而有:

3 结 语

在 Hilbert 空间及C*-代数的研究中,投影是非常重要的概念.投影的正交性是研究投影的核心概念,有着举足轻重的作用.本文研究发现，投影的 Birkhoff-James 正交与普通正交有很大的差别,这为研究 Hilbert 空间和C*-代数提供了新思路.