基于离散元的货舱内铁精矿运动数值研究

李筱航，张建伟，吴文锋，卢金树

(浙江海洋大学船舶与海运学院，浙江舟山 316022)

国际海事组织于2011 年颁布了IMSBC 规则，其将固体散装货物分为A、B、C 三组，其中A 组为易流态化货物。流态化是指散货船在航行过程中遭遇海浪产生摆动与振动，货物内部水分渗出，形成自由液面并发生运动，船舶复原力矩减小而稳性降低，导致事故发生。针对该类问题，周健等[1]采用PFC3D 对散装铁精矿流态化的宏观情况进行了研究。SPANDONIDIS，et al[2]基于分子动力学方法对货舱中固体颗粒的静止角、材料属性与运动特性间的联系进行了研究。宋喜庆等[3]结合离散元与有限元方法，对颗粒运动特性进行了研究。李文颉等[4]通过静倾斜实验得出含水率和库伦摩擦间的关系，并基于离散元法通过改变含水量，提出了船舶稳性数值评估方法。CHEN Wei，et al[5]建立了新的货物临界应力条件模型，为评估货物稳定性提供了一种手段[5]。DE BLASIO[6]通过增大颗粒间作用力来模拟黏性力，在分子动力学基础上建立了一套黏性物质颗粒的流动方法等。

目前，易流态货物在货舱内的运动规律研究日趋深入。为更清晰、直观地展示舱内颗粒货物运动情况及主要影响因素，基于离散元法，设计了共11 种计算工况，研究颗粒间摩擦系数、粒径级配、颗粒碰撞恢复系数、货舱横摇幅值及装载深度等因素对舱内铁精矿颗粒运动的影响，以期为易流态货物海上安全运输提供参考。

1 数值模型建立

1.1 理论模型

根据牛顿第二定律，颗粒i 的运动方程如下：

式中：mi—颗粒i 的质量；Ii—颗粒i 的转动惯量；—颗粒i 的加速度；—颗粒的角加速度；F—颗粒在质心处所受的合力；M—颗粒在质心处所受的合外力矩[7]。

颗粒间接触模型采用Hertz-Mindlin (no slip)接触模型[8]。其中，颗粒间接触法向力Fn可由下式计算：

式中E*为等效弹性模量，R*为当量半径，α 为接触半径。

利用中心差分法对式(1)进行数值积分，可得到两次迭代时间中间点表示的更新速度为：

式中：Δt—时间步长；N—对应的时间t。

对式(3)进行积分，可得到如式(4)所示的位移等式：

将计算得到的位移带入位移-力的关系中可以获得新的作用，然后反复迭代计算，可获取每一时刻颗粒受到的力和所处的位置。计算流程如图1 所示，首先获得初始接触力Fi根据牛顿第二定律求出ui，然后根据位移和力的关系再得出Fi，继而进行迭代计算。

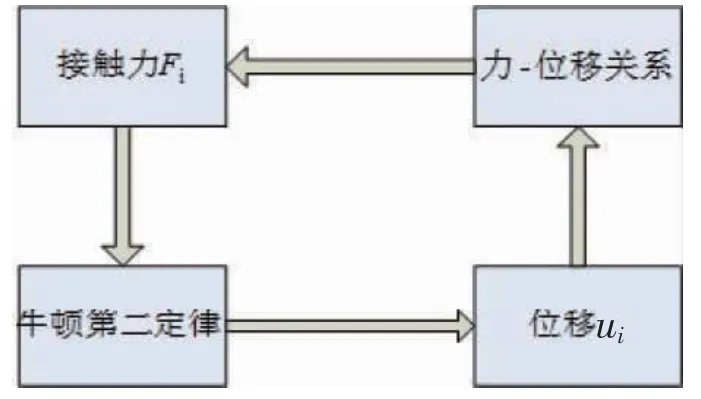
图1 离散元方法流程图Fig.1 Flow chart of discrete element method

1.2 模型验证

基于文献[1]进行本文数值模型验证，仿真参数见表1。三维方箱做x 方向的简谐往复运动，频率1 Hz，振幅60 mm。仿真对比结果如图2 所示，从颗粒整体运动表面轮廓可见，本文数值计算结果与文献结果基本一致。可能的误差在于：颗粒生成方式随机，颗粒的初始状态不能完全一致。

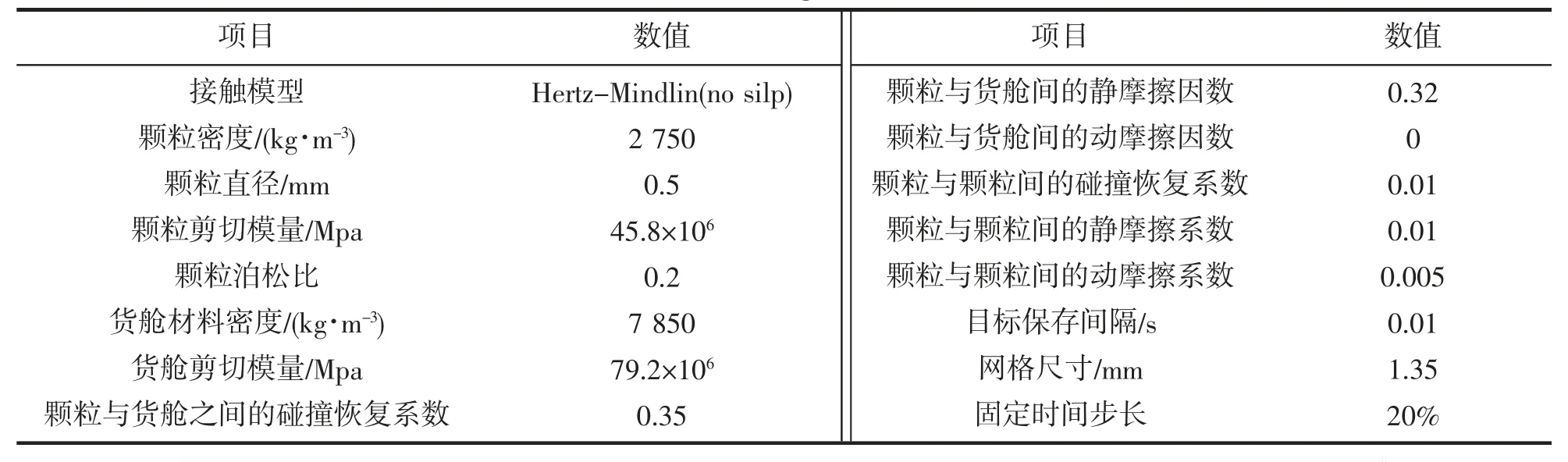
表1 模型验证仿真参数设置Tab.1 Parameter settings of model validation

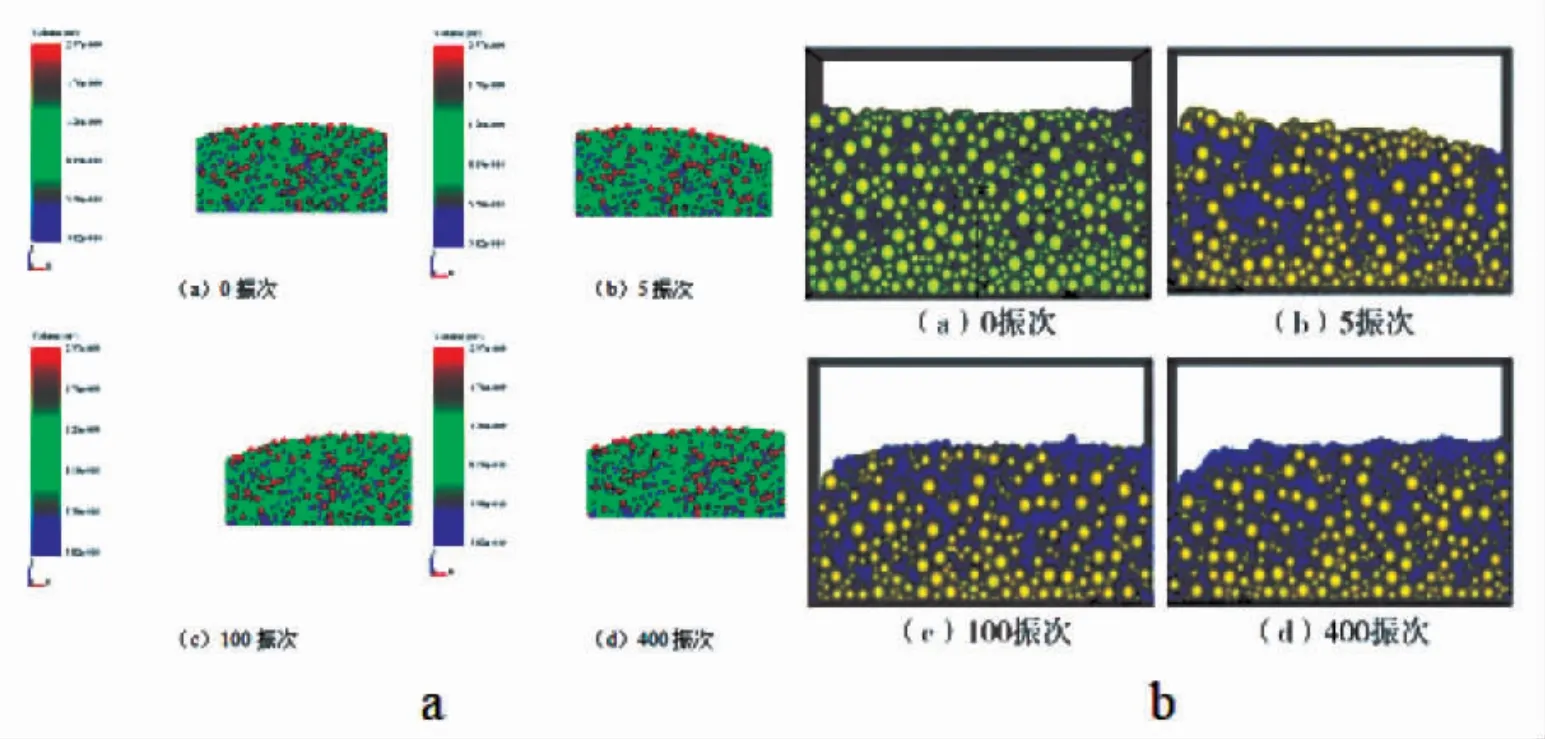
图2 结果对比：(a)本文数值计算结果(b)文献结果[1]Fig.2 Comparison of results：a：the present results b：results from reference[1]

2 研究方案

2.1 物理模型

以57 000 DWT 散货船典型货舱为原型[9]，考虑到数值模拟的局限性，考虑几何缩尺比为1：660，实船货舱及模型尺寸见表2 及图3 所示。

表2 57 000 DWT 散货船典型舱段及计算模型主尺度Tab.2 Typical sections of a 57 000 DWT bulk carrier and main dimensions of calculation model

货舱模型如图3 所示。

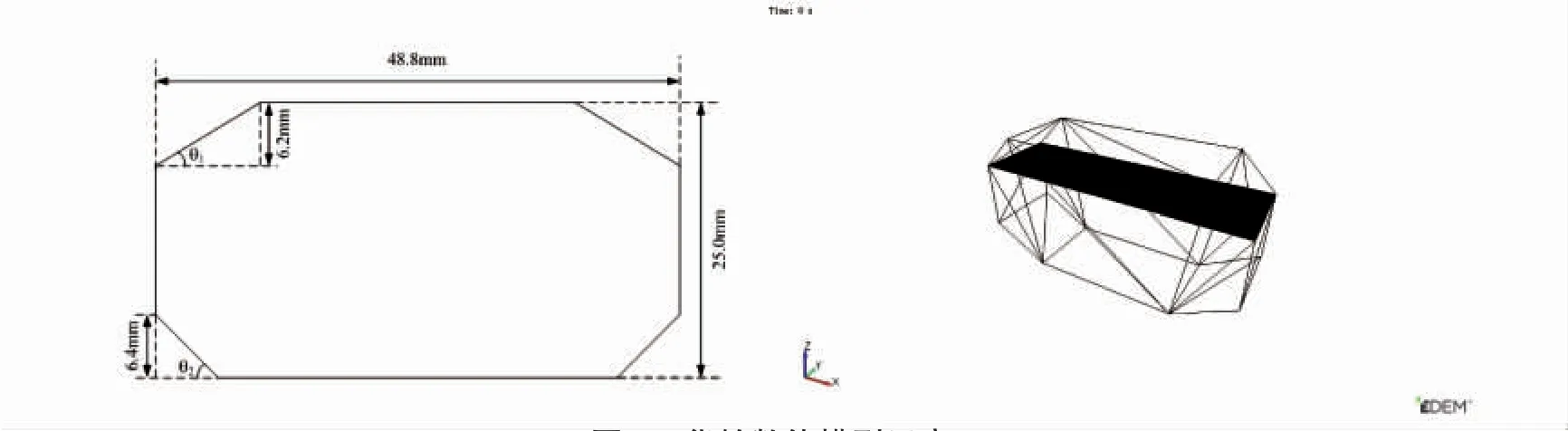
图3 货舱数值模型示意Fig.3 The cargo hold model

2.2 仿真工况

铁精矿是我国主要的进口矿石货种，也是易流态货物海运事故高发货种，与其他A 组货物相比，其具有较高的比重，颗粒具有多层、微孔结构等特点[10]。鉴于数值模型验证的可获得性，研究选取铁精矿作为研究对象，其颗粒属性参数见表1。考虑到易流态化货物的材料属性及船舶在海上运输的外部条件等因素，选取横摇幅值、货物装载情况、摩擦系数、粒径级配及颗粒碰撞恢复系数进行研究。具体参数如表3 所示。

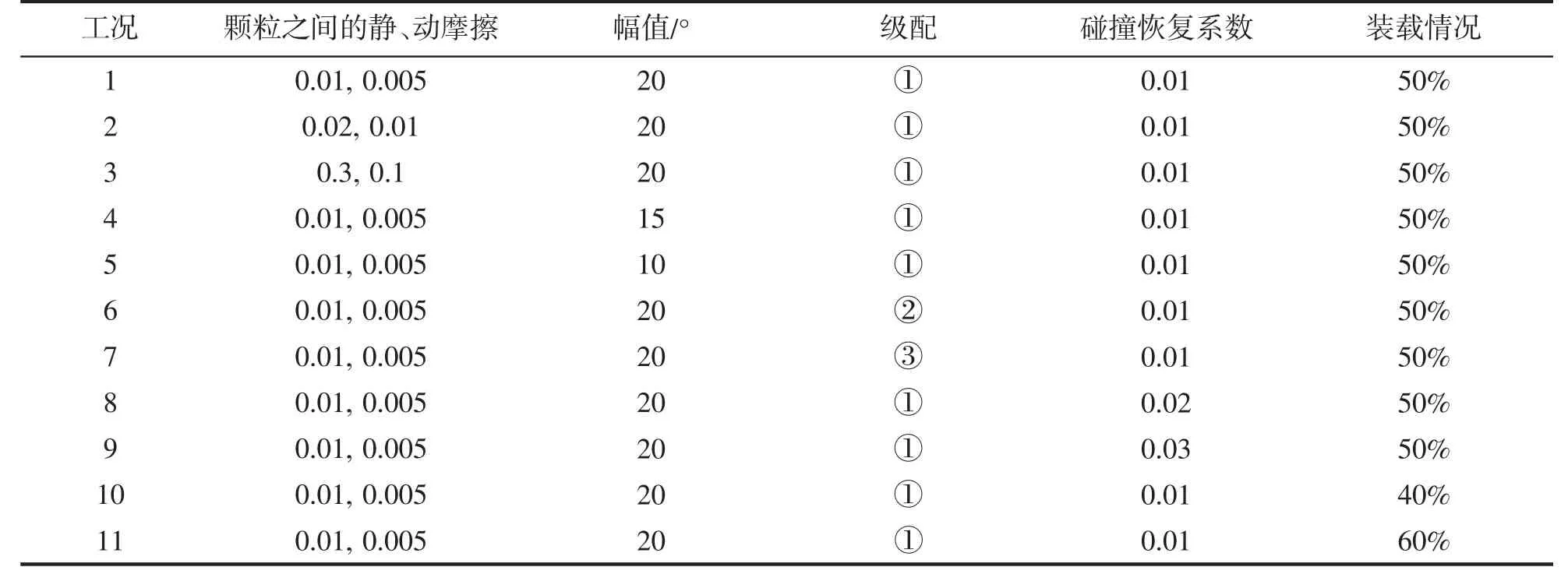
表3 计算条件设置Tab.3 Simulation conditions

利用User Defined 模块配置粒径级配，级配①为0.45 mm (10%)、0.6 mm (70%)、0.85 mm(20%)；级配②为0.45 mm (20%)、0.6 mm (60%)、0.85 mm (10%)；级配③为0.45 mm (10%)、0.6 mm (60%)、0.85 mm (30%)。运动形式为横摇，由于实际运输中颗粒运动比较缓慢，为加速颗粒运动，设定横摇周期为1 s，摇摆中心为形心。时间步长20%，网格大小为颗粒的3 倍最小半径，网格数为101 250 个。

3 结果分析

3.1 摩擦系数对铁精矿颗粒运动的影响

不同摩擦系数下颗粒运动情况如图4，可知工况1 颗粒倾斜程度最大，工况2 次之，工况3 颗粒倾斜程度最小，颗粒几乎没有流动。可见，颗粒库伦摩擦系数越大，颗粒越不易发生流动。

图4 9.75 s 时工况1(左)、2(中)、3(右)的颗粒分布情况Fig.4 Particle distribution of condition 1 (left),2 (middle) and 3 (right) at 9.75 s

颗粒法向接触力为颗粒的法向冲击力，其越大代表颗粒的碰撞次数越多、频率越高、颗粒运动更剧烈，颗粒的动能是衡量颗粒运动速度的重要标志。特殊强调的一点是，当颗粒静止不动时，也就是当时间为0时，在重力作用下，颗粒之间的法向接触力为0.000 88 N。

工况1、2、3 颗粒法向接触力、动能和重心偏移量对比如图5 所示。可知摩擦系数越小，颗粒间的法向接触力越大，颗粒的碰撞更剧烈，颗粒的法向接触力随着摩擦系数的增大而减少。摩擦系数改变后，颗粒的动能随着摩擦系数的增大而减小。随着摩擦力的增大，颗粒的重心偏移量变化越小，且在单个工况下，随着时间的增加，在惯性的作用下颗粒难以返回初始位置，颗粒的行程会越来越大，导致货物整体重心偏移量变大。

图5 工况1、2、3 时法向接触力(左)、颗粒动能(中)和重心偏移量(右)变化曲线Fig.5 Variation of normal contact force (left),particle kinetic energy (middle) and center of gravity deviation (right) under conditions 1,2 and 3

3.2 横摇幅值对铁精矿颗粒运动的影响

工况1、4、5 的仿真结果对比如图6 所示，横摇幅度越大，法向接触力变化越明显，峰值越大。三种工况随着横摇幅值的减小，颗粒动能递减，货物整体重心偏移量明显减小。

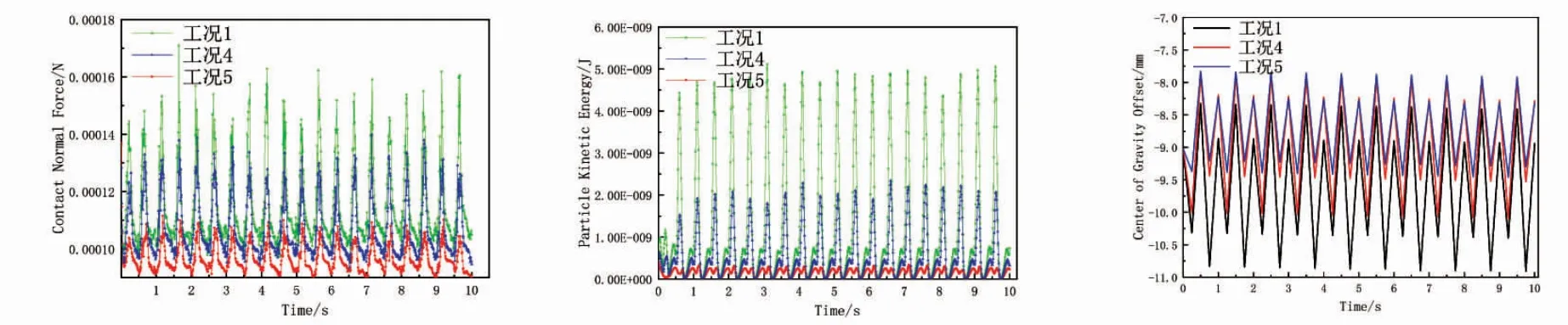
图6 工况1、4、5 时法向接触力(左)、颗粒动能(中)和重心偏移量(右)的变化曲线Fig.6 Variation of normal contact force (left),particle kinetic energy (middle) and center of gravity deviation (right) under conditions 1,4 and 5

3.3 粒径级配对铁精矿颗粒运动的影响

工况1、6、7 的数据对比如图7。半载情况下，工况1、6 和7 分别装载颗粒4 450 个、7 810 个和6 450个。从图7 可以看出颗粒数量与颗粒碰撞程度成反比。工况6 与工况7 的动能峰值相差不大，工况6 的颗粒动能峰值略大，工况1 的颗粒动能峰值远远高于其他两个工况。装载深度相同的情况下，颗粒越多重心越高，但重心偏移量相差不明显。

图7 工况1、6、7 下法向接触力(左)、颗粒动能(中)和重心偏移量(右)的变化曲线Fig.7 Variation of normal contact force (left),particle kinetic energy (middle) and center of gravity deviation (right) under conditions 1,6 and 7

3.4 碰撞恢复系数对铁精矿颗粒运动的影响

工况1、8、9 的数据对比如图8，可知颗粒法向接触力几乎没有差别，并且3 种工况下的颗粒动能变化曲线完全一样。由此可见，不同的碰撞恢复系数对颗粒的法向接触力和动能并没有较大影响。3 种工况的重心偏移量也基本相同。

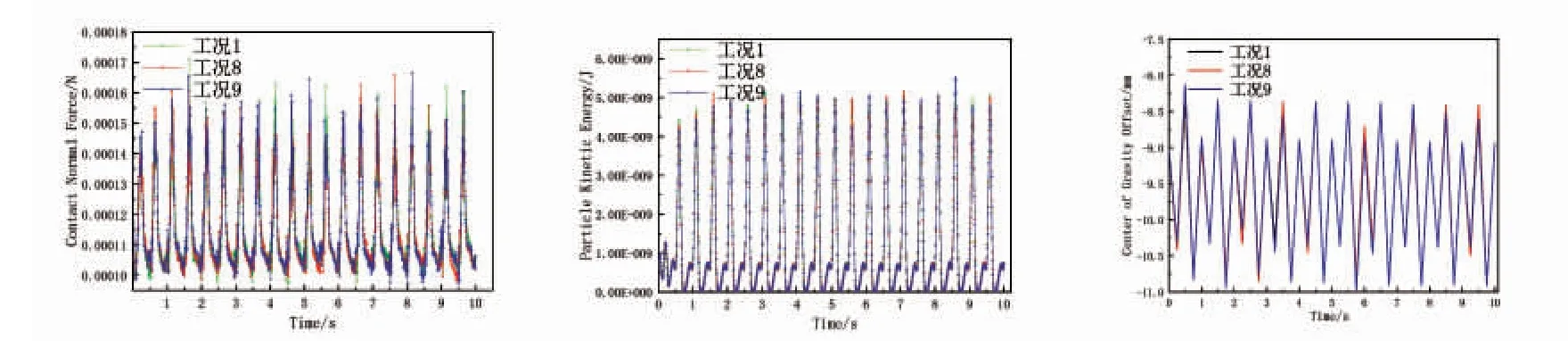
图8 工况1、8、9 时法向接触力(左)、颗粒动能(中)和重心偏移量(右)的变化曲线Fig.8 Variation of normal contact force (left),particle kinetic energy (middle) and center of gravity deviation (right) under conditions 1,8 and 9

3.5 货物装载情况对铁精矿颗粒运动的影响

工况1、10、11 的数据对比如图9，可知货物装载量与颗粒的碰撞程度成正比，工况1 和工况10 的法向接触力峰值基本相同，但工况1 的法向接触力变化幅度大，说明工况10 在高装载率下颗粒碰撞较为剧烈。工况1 和工况10 的颗粒动能几乎一样，工况1 的颗粒动能维持在一个较低的水平。工况11 颗粒的重心偏移量变化幅度更大，工况10 的重心偏移量变化幅度最小。

图9 工况1、10、11 法向接触力(左)、颗粒动能(中)和重心偏移量(右)的变化曲线Fig.9 Variation of normal contact force (left),particle kinetic energy (middle) and center of gravity deviation (right) under working conditions 1,10 and 11

4 结论

本文通过与其他文献结果进行对比验证了模型的正确性，确定了11 种工况，对散货船货舱内的铁矿石颗粒在不同工况下的运动情况进行了数值模拟，通过改变摩擦系数来代替不同含水量的影响，得出以下结论：

(1)本研究通过改变颗粒间摩擦系数来替代含水量的影响具备正确性和可行性，本文构建的铁精矿颗粒舱内运动数值仿真模型能够正确处理颗粒材料在舱内的运动仿真。

(2)颗粒摩擦系数增加即货物含水量增加，则颗粒运动幅度明显降低；单个工况下，由于惯性的作用，颗粒的运动幅度随时间的延长不断增加。横摇幅值的增加会导致颗粒碰撞更加剧烈，颗粒的重心偏移量变化幅度会更大；碰撞恢复系数的改变对颗粒的运动情况几乎没有影响；在装载体积一定的情况下，颗粒越少的粒径级配，颗粒的运动幅度越大；随着颗粒装载的增多，颗粒的法向接触力和动能会维持在一个更高的水平。