ANALYSIS OF AN EPIDEMIC MODEL WITH CROWLEY-MARTIN INCIDENCE RATE AND HOLLING TYPE II TREATMENT∗†

Liuqing YangFengying Wei

(1.College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,Fujian,PR China; 2.Key Laboratory of Operations Research and Control of Universities in Fujian,Fuzhou University,Fuzhou 350108,Fujian,PR China)

Abstract

Keywords epidemic model;Crowley-Martin incidence rate;extinction;persistence

1 Introduction

Spread of infectious diseases normally have showed great impacts upon individuals health and society economy,even upon social panic and extinction for some species.Then in applications,how to prevent and control infectious diseases is a challenge for human being.And in the view of mathematicians,prevention and control of infectious diseases will be a main topic when human beings encounter modified epidemic models,which usually consider the susceptible (S,for short) ,the infected (I,for short) and the recovered (R,for short) to be basic compartments of a total population.For instance,some epidemic models[1–5]described spread mech-anisms and Diffusion approaches for some specific topics.Recent contributions have discussed epidemic models in multiple views.We here mentioned that the interactions between the susceptible and the infected have been paid much attention for several decades.For example,some researchers considered that interaction between susceptible individuals might be restricted by their own density,hence a saturated incidence rate[6,7]was introduced into epidemic models instead of bilinear incidence rateαSI[8],whereαmeans the infection rate andβdenotes the saturation constant which describes the epidemiological spread of infectious diseases.Here,Zhanget al.analyzed an SIR epidemic model with incubation time and saturated incidence ratein[6],in which they showed that if the basic reproduction number satisfiesR0<1,the disease-free equilibrium is globally asymptotically stable and the disease dies out.While for the caseR0>1,the epidemic model admits an endemic equilibrium.Similarly,saturated incidence ratewas also extensively considered by authors,among which the inhibitory effect of infected individuals was more focused,see[9–11]and references therein.And also,several types of incidence rates have been raised,for example,[12,13]involved Beddington-DeAngelis type incidence rate,and Crowley-Martin type with form ofwas considered in[14–17].

Epidemic models with saturated treatment rate were extended by authors in[21–23].Especially,Upadhyayet al.[23]proposed the following SEIR model with Crowley-Martin incidence rate and treatment functionh(I) :

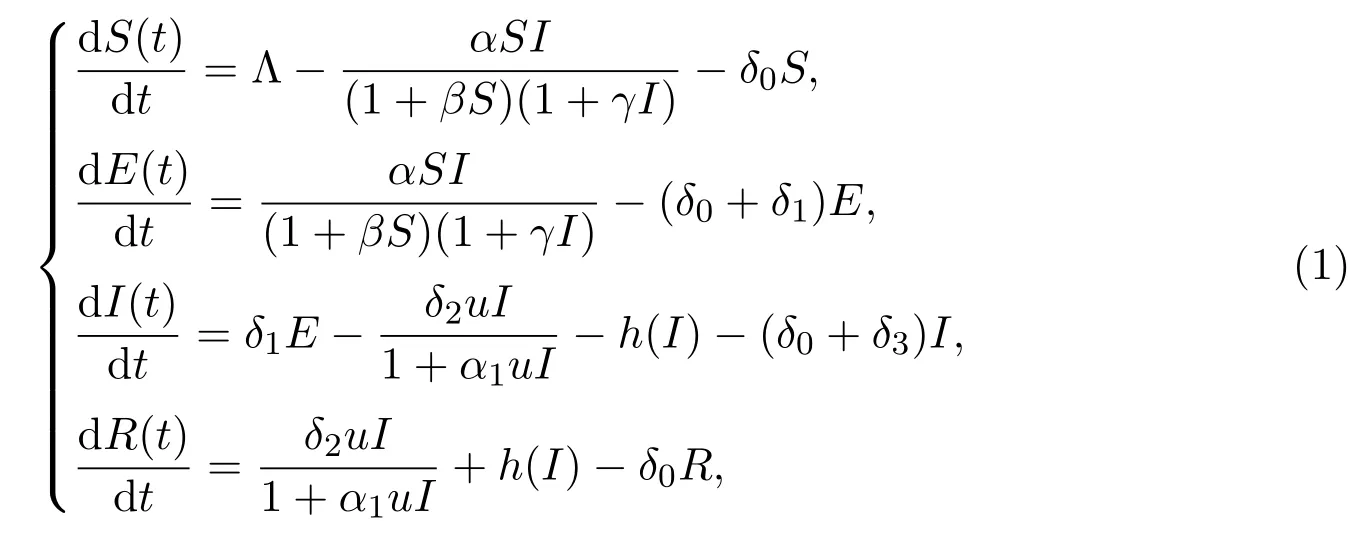
whereE(t) represents the density of exposed individuals at timet,andδ0is the natural death rate,δ1means the transmission rate fromEtoI,andδ3indicates the death rate of disease,uis the treatment control constant,δ2andα1are non-negative.The treatment functionh(I) here is displayed by

or

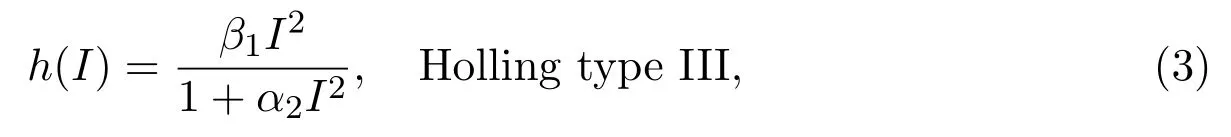
whereα2is the half-saturation constant.

Treatment is a key aspect for the control of diseases,such as measles,tuberculosis and flu.It was turned to be a simple form in Wang and Ruan[18],in which they presented an SIR epidemic model with a piecewise constant treatment function shown below:

whereβ1is the treatment rate.Later,Wang[19]modified (4) ,and extended it into a new form with limited treatment sources:

withm=β1I0,which indicates that the treatment rate is a constant when the capacity of treatment is reached.Further work was established by Eckalbar and Eckalbar in[20]with a quadratic treatment function.

We are inspired by[23]and consider vaccinated compartment and fluctuations within epidemic model (1).Precisely speaking,a new classV(t) is naturally introduced since some diseases can be prevented and controlled to a certain extent with gradual improvement of new drags and vaccines.Another fact in real situations,is that the fluctuated climate and temperature are often encountered,therefore we derive an epidemic model with environmental fluctuations as follows:

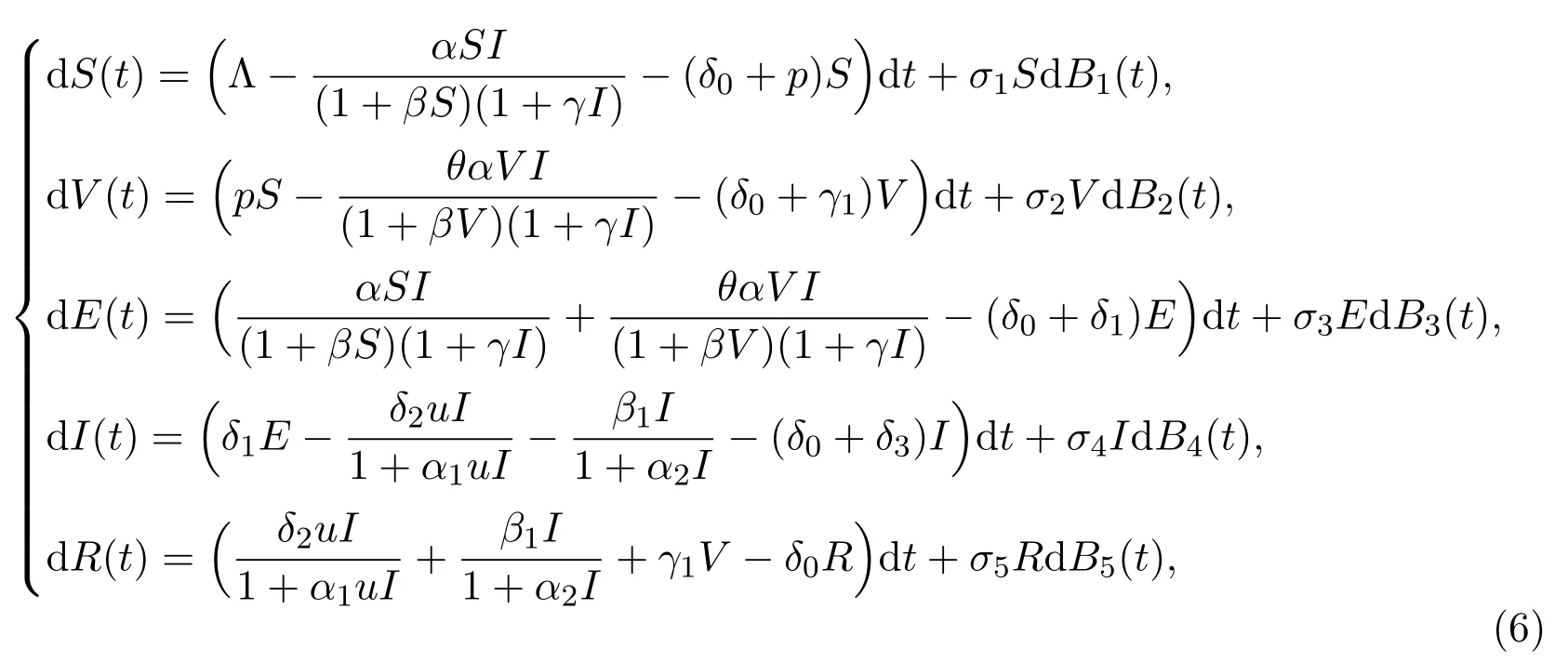
wherepis probability of vaccination,γ1denotes individuals who obtain immunity and move into the recovered,andθαrepresents the average number of effective contacts of a vaccinated individual per unit time.All parameters referred in the epidemic model (6) are positive constants.Andσi>0 (i=1,···,5) are the intensities of white noises,Bi(t) (i=1,···,5) denote standard independent Brownian motions which are defined on a complete probability space (Ω,{Ft}t≥0,P) with its filtration{Ft}t≥0satisfying the usual condition,in other words,it is right continuous andF0contains all P-null sets.

The organization of this paper is composed by three parts.In Section 2,the existence and uniqueness of a global solution to model (6) are verified.Next,we find that disease tends to extinct underR0<1 in Section 3.In Section 4,sufficient conditions for persistence are established by constructing Lyapunov functions.As a consequence,a conclusion part ends this work.

2 Existence and Uniqueness of Positive Solution

In this section,we firstly demonstrate that model (6) admits a unique global positive solution.

Theorem 2.1Model(6)has a unique globalpositivesolutionont≥0for any initial valuein.

ProofCoefficients of model (6) satisfy local Lipschitz condition,so there exists a uniq ue local solutionfor any initial value,whereτeis the explosion time as expressed in[24].Then we just to prove the assertionτe=∞is valid almost surely.To this end,letm0>1 be sufficiently large such that each component oflies within closed interval.For each integerm≥m0,defining the stopping time as cited in[24]

herewith we denote inf∅=∞.Obviously,we find thatτmis increasing asm→∞.Then we set,and have an inequalityτ∞≤τe.Next,we only to demonstrate the assertionτ∞=∞almost surely.If the assertion is false,then there exist a pair of constantsT>0 andε∈(0,1) satisfying P{τ∞≤T}≥ε.Hence there is an integerm1≥m0such that P{τm≤T}≥ε.Define aC2-functionas follows:

whereKis a positive constant.The remaining of proof can be derived by[33].Here we omit it.The proof is complete.

3 Extinction of the Disease

To investigate sufficient conditions for the extinction of infectious diseases.Wefirstly calculate the basic reproduction numberR0of deterministic model (σi=0) by use of next generation matrix (see[25–27]) as follows:

Therefore,we derive the following results

The proof is complete.

4 Persistence in the Mean

On the other hand,the persistence in the mean of disease is also a vital aspect.In this section,we mainly study this property by constructing suitable Lyapunov functions.The result is presented in Theorem 4.1.In order to smooth the proof,we start from Lemma 4.1 by as demonstrated in Lemmas 2.1 and 2.2 in[31,32].

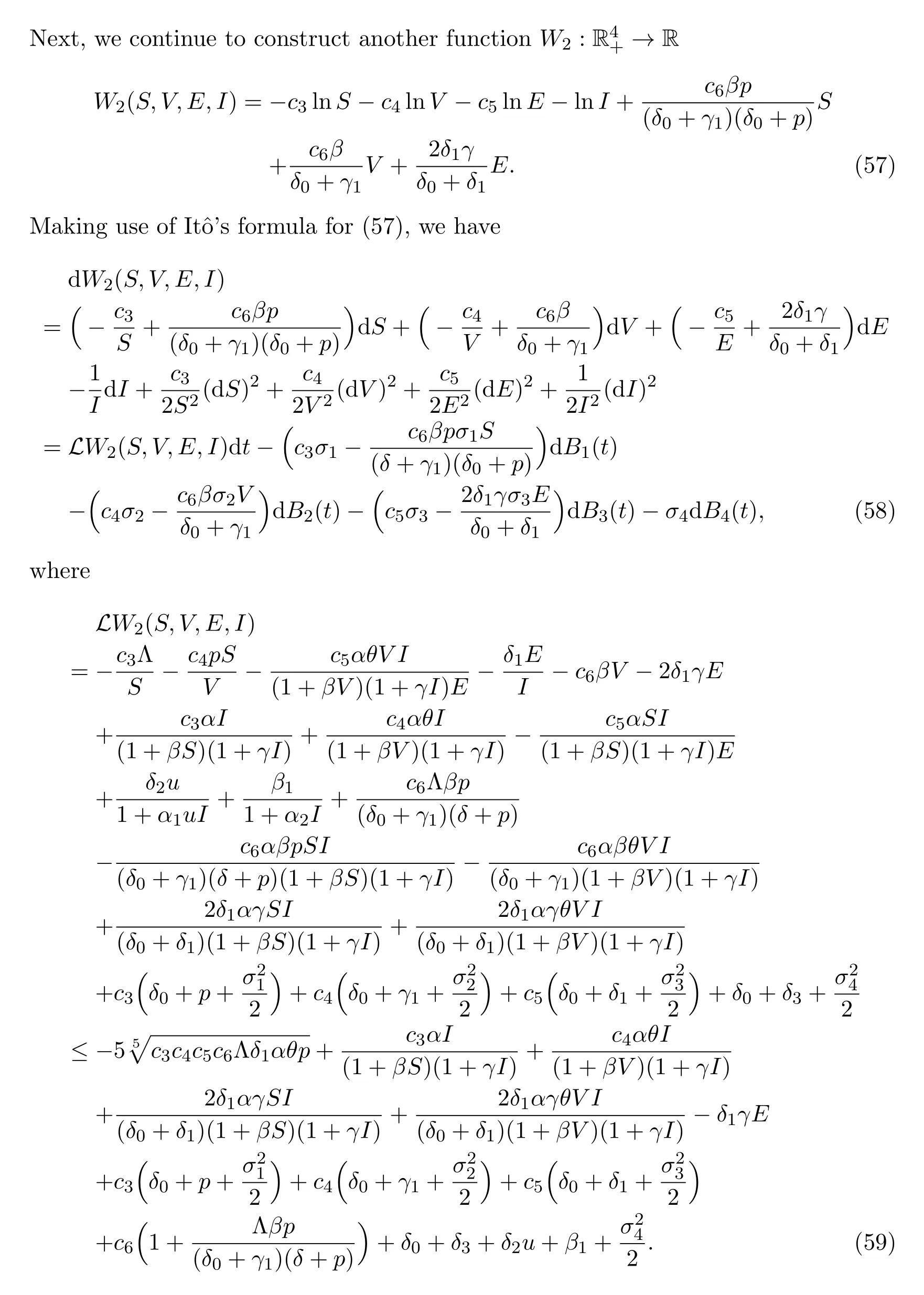
5 Conclusions

In this paper,we fucus on the extinction and persistence of an epidemic model with Crowley-Martin incidence rate and Holling type II treatment by constructing reasonable Lyapunov functions.

We firstly obtain that model (6) admits a unique global positive solution by defining stopping time and It’s formula.And we also figure out,if the basic reproduction number satisfiesR0<1,andandν<0 hold in Theorem 3.1,then diseases will die out in a long run,where the intensitiesσ1,σ2andσ3are key fluctuation coefficients therewith.Further,we also notice that the valveνdecreases when environmental fluctuations increase,and the larger the treatment rateβ1the earlier the infected individuals reach extinction.

In addition,we derive that model (6) keeps solution persistent in the mean,if the threshold value(depends on fluctuation coefficientsσ1,σ2,σ3andσ4) is positive.Moreover,when the intensities of environmental fluctuations increase,the threshold valuebecomes smaller (that is,the time for persistence to infected individuals might decline).Further,the persistence of infected individuals maintains a lower level when the value of treatment rateβ1increases.