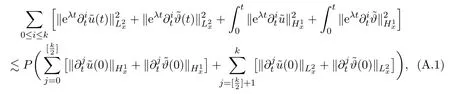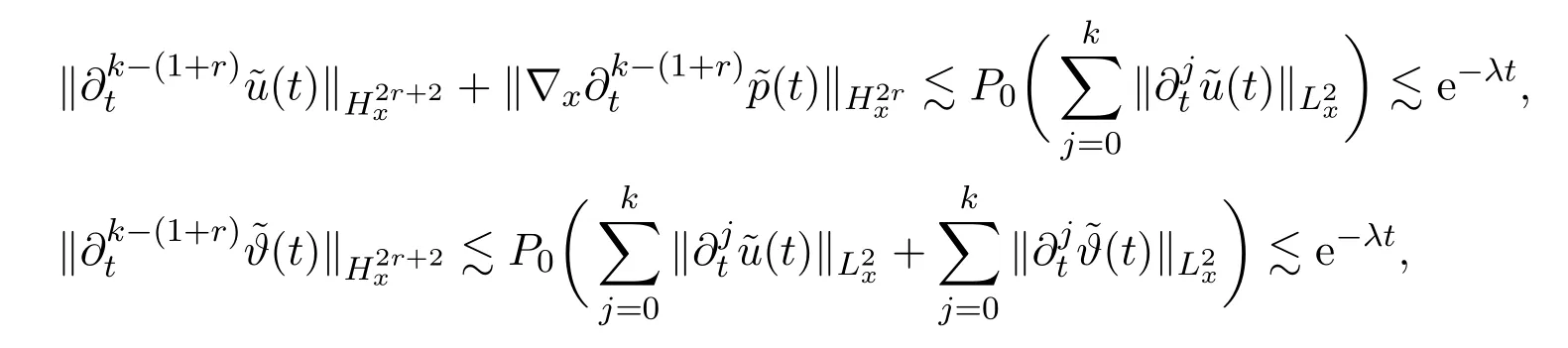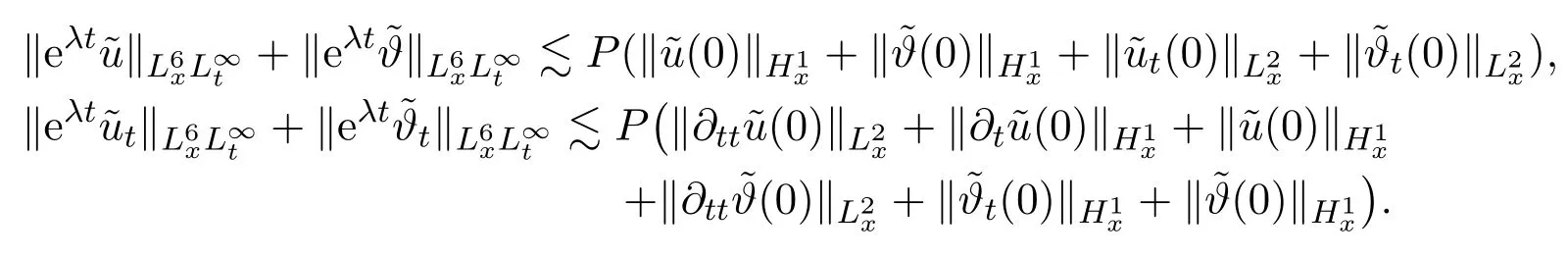DIFFUSIVE LIMITS OF THE BOLTZMANN EQUATION IN BOUNDED DOMAIN∗†
2020-07-02RaffaeleEsposito
Raffaele Esposito
(International Research Center M &MOCS,Univ.dell’Aquila,Cisterna di Latina, (LT) 04012 Italy)
Yan Guo‡
(Division of Applied Mathematics,Brown University,Providence,RI 02812,U.S.A.)
Chanwoo Kim
(Department of Mathematics,University of Wisconsin,Madison,53706-1325 WI,U.S.A.)
Rossana Marra
(Dipartimento di Fisica and Unit INFN,Universit di Roma Tor Vergata,00133 Roma,Italy)
Abstract
Keywords steady and unsteady Boltzmann equation;hydrodynamics limits;boundary effects
1 Introduction
1.1 Hilbert Expansion with No Boundary Layer Approximations
The hydrodynamic limit of the Boltzmann equation has been the subject of many studies since the pioneering work by Hilbert,who introduced his famous expansion in the Knudsen numberεin[37,38],realizing the first example of the program he proposed in the sixth of his famous questions[39].Mathematical results on the closeness of the Hilbert expansion of the Bolzmann equation to the solutions of the compressible Euler equations for small Knudsen numberε,were obtained by Caflisch[14],and Lachowicz[45],while Nishida[47],Asano and Ukai[4]proved this by different methods.
On a longer time scaleε−1,where Diffusion effects become significant,the problem can be faced only in the low Mach numbers regime (Mach number of orderεor smaller) due to the lack of scaling invariance of the compressible Navier-Stokes equations.Hence the Boltzmann solution has been proved to be close to the incompressible Navier-Stokes-Fourier system.Mathematical results were given,among the others,in[11,18,31,33,34]for smooth solutions.For weak solutions (renormalized solutions) ,partial results were given,among the others,in[7–10],and the full result for the convergence of the renormalized solutions has been obtained by Golse and Saint-Raymond[27].
Much less is known about the steady solutions.It is worth to notice that,even for fixed Knudsen numbers,the analog of DiPerna-Lions’renormalized solutions[19]is not available for the steady case,due to lack ofL1and entropy estimates.In[29,30],steady solutions were constructed in convex domains near Maxwellians,and their positivity was left open.The only other results are for special,essentially one dimensional geometry (see[3]for results at fixed Knudsen numbers and[1,2,22,23]for results at small Knudsen numbers in certain special 2D geometry).In a recent paper[20],via a newL2−L∞framework,we have constructed the steady solution to the Boltzmann equation close to Maxwellians,in 3D general domains,for a gas in contact with a boundary with a prescribed temperature profile modeled by the diffuse reflection boundary condition.The question about positivity of these steady solutions was resolved as a consequence of their dynamical stability.As pointed in[25],despite the importance of steady Navier-Stokes-Fourier equations in applications,it has been an outstanding open problem to derive them from the steady Boltzmann theory.
The goal of our paper is to employ theL2−L∞framework developed in[20]to study the hydrodynamical limit of the solutions to the steady Boltzmann equation,in the low Mach numbers regime,in a general domain with boundary where a temperature profile is specified.We refer to[15,16,41–44]for the recent development ofL2−L∞framework in various directions.
Let Ω be a bounded open region of Rdfor eitherd=2 ord=3.We consider the Boltzmann equation for the distribution densityF(t,x,v) witht∈R+:=[0,∞) ,x∈Ω,v∈R3.In the diffusive regime,the time evolution of the gas,subject to the action of a fieldis described by the followingrescaledBoltzmann equation:

where the Boltzmann collision operator is defined as
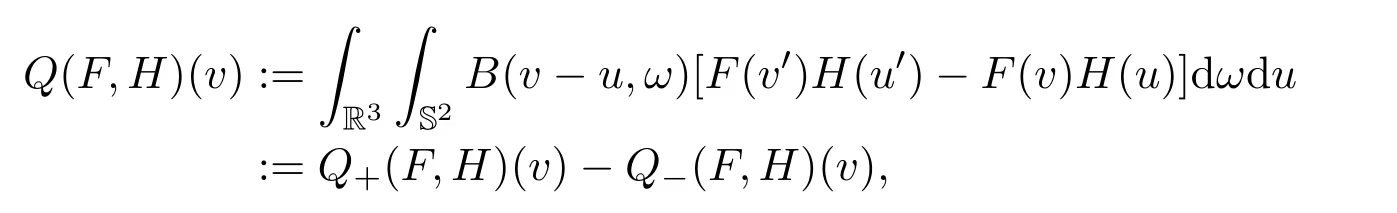
withv′=v−[ (v−u)·ω]ω,u′=v+[ (v−u)·ω]ω.Here,Bis chosen asthe hard spheres cross sectionthroughout this paper,

The interaction of gas with the boundary∂Ω is given by the diffuse reflection boundary condition,defined as follows:Let

be the local Maxwellian with densityρ,mean velocityu,and temperatureT.For a prescribed functionTwon∂Ω,we define

We imposethe diffuse reflection boundary conditionas

where

Here,we denote byn(x) the outward normal to∂Ω atx∈∂Ω and decompose the phase boundaryγ:=∂Ω×R3as
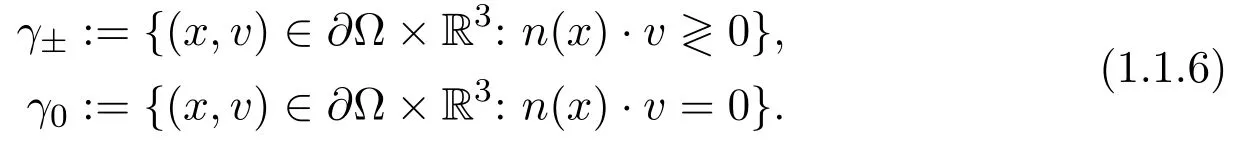
We remind that the boundary condition (1.1.4),(1.1.5) ensures the zero net mass flow at the boundary:

The rescaled Boltzmann equation (1.1.1) is studied under the assumption of low Mach numbers,meaning that the average velocity is small compared to the sound speed.This can be achieved by looking for solutions

withthe global Maxwellian
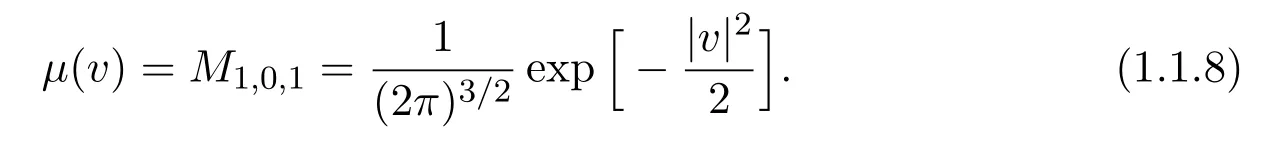
Here,the number M is proportional to the Mach number.The case of M=εcorresponds to the incompressible Navier-Stokes-Fourier limit (INSF) that will be discussed in this paper.The case of M≪εcorresponds to the incompressible Stokes-Fourier limit and the results of this paper also cover this case which will not be discussed explicitly.
The condition (1.1.7) ,once assumed initially,needs to be checked at later times.By multiplying (1.1.1) byvand integrating on velocities,we see that the change of mean velocity is proportional toThus,we need to assume=MΦ with a bounded Φ.Moreover,to make (1.1.7) compatible with the boundary conditions,we need to assume thatTw=1+Mϑw.In particular,for the INSF case,we have

The presence of the boundary represents a major issue in pursuing such a program.The usual approach is based on the representation of the solution by means of an Hilbert-like expansion in the bulk,suitably corrected at the boundary to satisfy the boundary conditions[1,2,22,23]:

Here,the functionsfkare corrections in the bulk,whileare boundary layer corrections which solve Milne-like problems,andR=Rεdenotes the remainder.It is important to choose sufficiently largek≥1 so that the nonlinear collision term can be controlled.The corrections at the boundary are computed by means of a boundary layer expansion which,in a general domain,presents some issues hard to deal with.The usual strategy is to solve thek-th term of the boundary layer expansion by looking at it in terms of the rescaled distance from the boundary (see e.g.[48]).Using of such a variable,the problem looks like a half-space linear problem (Milne problem) [5]with a correction due to the geometry which can be interpreted as an external field of the order of the Knudsen number.The field,due to thek-th term of the boundary layer expansion,is usually included as source term in the equation for the (k+1) -th term[48],but the lack of regularity makes this hard to control.
This strategy has been used in[12]in the much simpler case of the neutron transport equations,but recently in[51]it has been proved that the result in[12]breaks down exactly because of the lack of regularity (see the recent work in the Boltzmann case[50]).Therefore,the geometric field,even if of small size,has to be included in the equation for thek-term of the expansion,as in[2,24]for the case of the gravity and[51]for the geometrical field in the neutron transport equation in a disk:
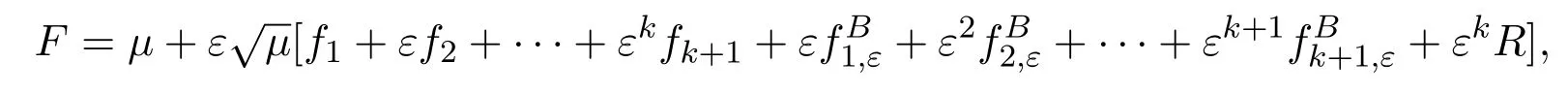
In this paper,weavoidthe boundary layer expansion to cope with a general geometry.This is possible because,in the incompressible regime,the first term of the bulk expansion in (1.1.10) which violates the boundary condition is of orderε2,while the main hydrodynamic contribution,is of orderε.We will discuss more about this in Section 1.3.
1.2 Expansion with Remainder
The Hilbert expansion suggests that the solution can be written as

whereµis the standard Maxwellian in (1.1.8).
To determinef1,f2andRs,we define the linearized collision operator as

and the nonlinear collision operator as

The null space ofL,NullLis a five-dimensional subspace ofL2(R3) spanned by

We denote the orthogonal projection offonto NullLas

and (I−P) the projection on the orthogonal complement of NullL.The inverse operatorL−1is defined as follows:L−1gis the unique solution ofL(L−1g)=g,and P (L−1g)=0.
The first correctionf1is given by

where (ρ,u,ϑ) represents the density,velocity,and temperature fluctuations.The density and the temperature fluctuations satisfy the Boussinesq relation

and the velocity and the temperature fluctuations satisfies the INSF system

where v is the viscosity andκis the heat conductivity.
The second correctionf2is given by
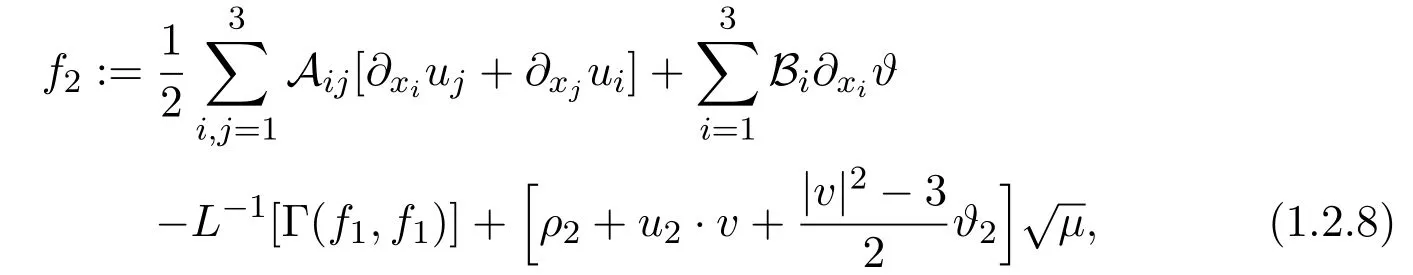
whereAijandBiare given by

Note that the only restriction onρ2,u2andϑ2turns out to be that∇x[ρϑ+ρ2+ϑ2]=∇xp.For simplicity we choose

where

These choices imply

By choosing the reference Maxwellian,we can assume

The equation forRis obtained by plugging (1.2.1) into (1.1.1) :
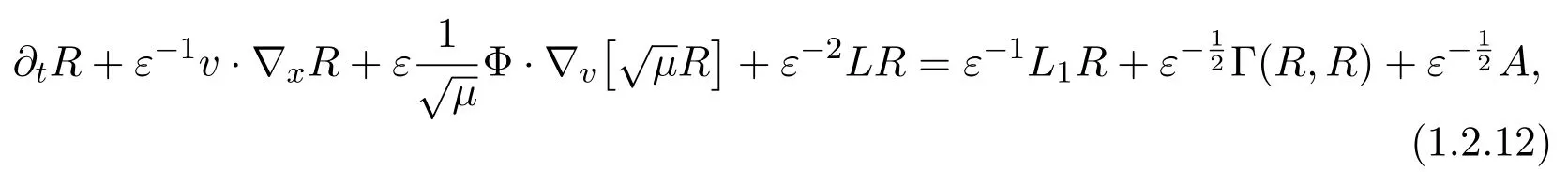
with

and

It is important to observe the fact thatsolves (1.2.7).As a consequence,Ais given by
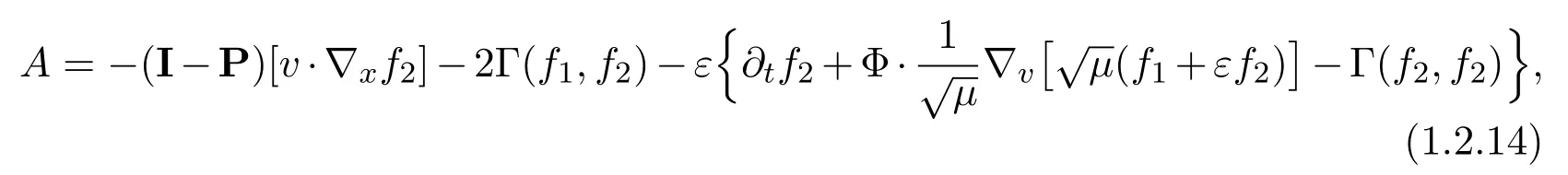
which implies the crucial fact that PA=O(ε).This is the only but essential point of our expansion where the specific hydrodynamic equations play a role.We also remark that,by (1.2.10) ,

It is well-known that (see[17])

where the collision frequency is defined as
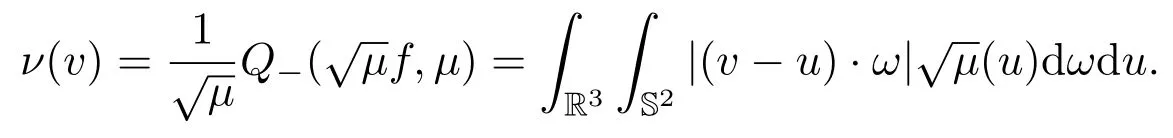
For the hard sphere cross section (1.1.2) ,there are positive numbersC0andC1such that,for

Moreover the compact operatorKis defined as
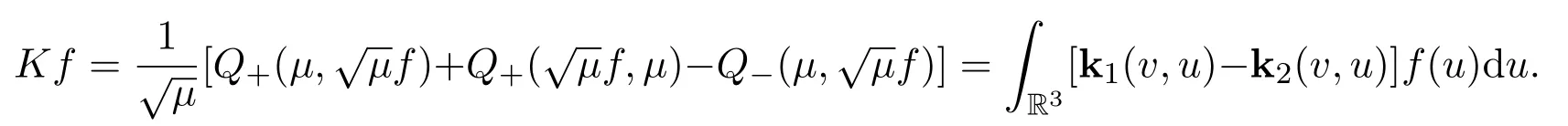
The operatorLis symmetric onL2(R3) : (f,Lg)2=(g,Lf)2where (·,·)2is theL2inner product.
The following spectral inequality holds forL:
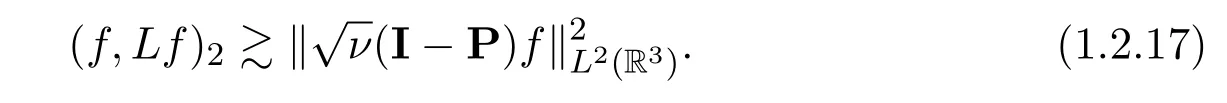
1.3 Boundary Conditions
We assume that (ρ,u,ϑ) satisfies the boundary conditions of (1.2.7) with (1.2.9).As a consequence,forx∈∂Ω,

Moreover,by expandingM1+ερ,εu,1+εϑinε,we get
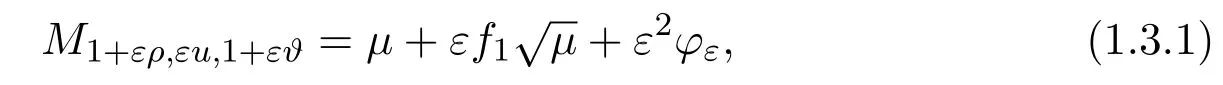


1.4 Main Results
We first focus on the steady case.The following (ps,us,ϑs) is a solution to the steady INSF with Dirichlet boundary conditions and subject to the external field Φ:

Note that,if Φ is a potential field,us≡0 is a solution to the above system.Therefore,in order to have a stationary solution with non vanishing velocity field,we may assume that Φ is not a potential field,such that∇x·Φ=0. (See[25])
The steady solution to the Boltzmann equation is obtained with the same procedure discussed before for the unsteady case:
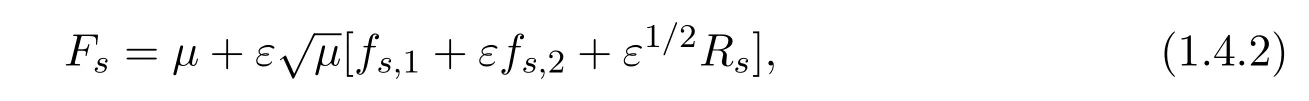
wherefs,1andfs,2are given by (1.2.5) and (1.2.8) withρ,u,ϑ,andpreplaced byρs,ϑs,usandps.The remainder has to satisfy the following equation

with the boundary condition (1.3.7).HereAsis given by (1.2.14) withf1,f2replaced byfs,1,fs,2,and satisfies the mean zero condition (1.2.15).
Theorem 1.1AssumeΩis an open bounded subset ofR3with C3boundary∂Ω.We also assume the hard sphere cross section(1.1.2).
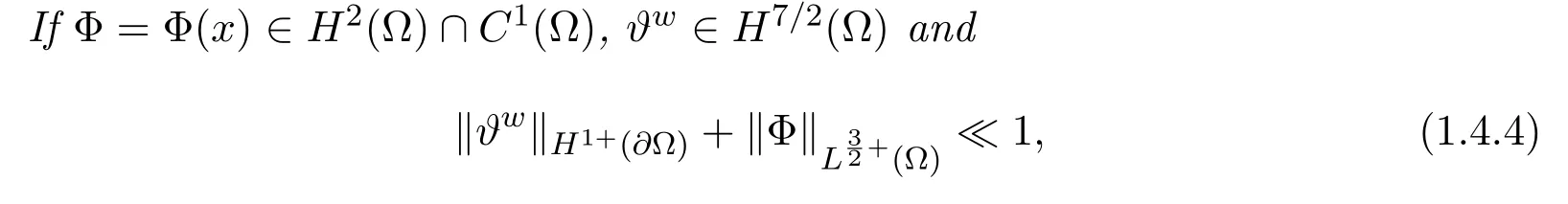
then,for0<ε≪1,there is a unique positive solution Fs≥0,given by(1.4.2)with Rssatisfying(1.4.3)and the boundary condition(1.3.7).Here,f1,sand f2,sare given by(1.2.5)and(1.2.8)where(us,ϑs,ps)solves(1.4.1).
Moreover,

where w(v)=eβ|v|2with0<β≪1.
We remark that in the expansion (1.4.2) ,the remainderεRsis of higher order inLpfor 2≤p<6.On the other hand,is of orderε−1/2inL∞,so the expansionisnotproved to be valid inL∞.It is important to note that the key difficulty in this paper is to control the ‘strong’nonlinear terms,in the absence of boundary layer approximations.The hard spheres cross section is needed to control the termεv·Φfcoming from the external field.
We use the quantitativeL2−L∞approach developed in[20],in the presence ofε.We start with the energy estimates to get

The missing PRscan be estimated by the coercivity estimates in[20],with carefully chosen proper test functions in the weak formulation,such that (Proposition 2.2) :
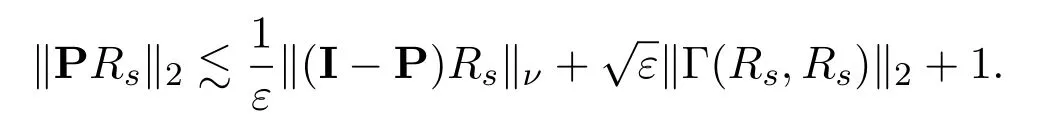
By using a double iteration of the Duhamel formula along the characteristics[20],we may bootstrap suchL2estimates toL∞estimate as

where the dimension isd=3.
We split

Since we expectε−1∥(I−P)Rs∥ν.1,the second part of the nonlinear term is estimated as


which is way out of control to close the estimates.
The key observation is that in ourL∞estimate,higher integrability of PRshelps to reduceεsingularity in the estimate of∥Rs∥∞.Indeed,if we have
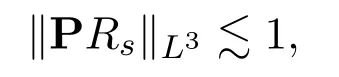
then,ind=3,we are able to improve theL∞estimate as (Proposition 3.3) :
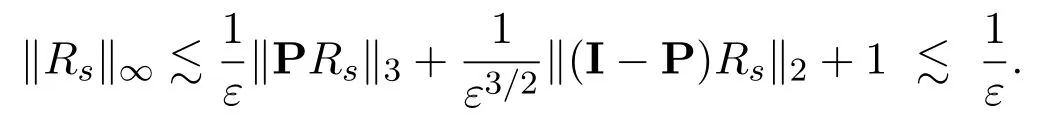
Now with such an improvement,we haveand the nonlinearity isexactlycontrollable:
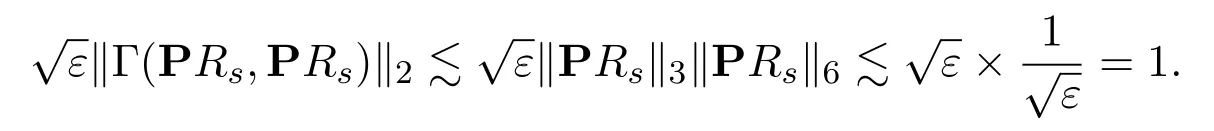
In the absence of the external field and the boundary,Φ≡0 and Ω=R3,such gain of integrability,∥PRs∥L3.1,is well-known from the Averaging Lemma[26]and the sharp Sobolev embeddingH1/2⊂L3(See also the case for a convex bounded domain with Φ≡0 in[26]).We need to extend this estimate properly to case of the bounded domain Ω with the presence of the external field Φ̸0.We first consider an extension ofRsto the whole space,denoted bys,such thats∈L2and

We circumvent this difficulty via an extension lemma,Lemma 2.4,which asserts that,for the function cutoff from the grazing setγ0,
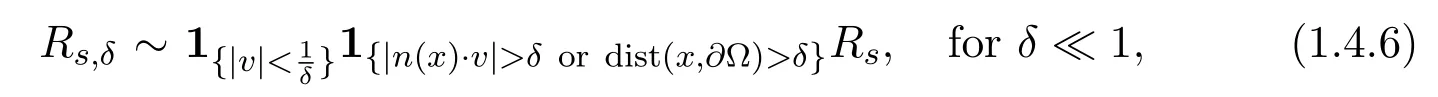
We also remark that in the presence of an external field,even the construction of the solution to the linear problem is delicate.In fact,an extension similar to (1.4.6) must be used again to gain compactness from the averaging lemma.Moreover,as in[20],our construction cannot yield the positivity ofFsdirectly,which is left for the unsteady case.
Next we investigate the stability properties of the stationary solution.To discuss this,we study the unsteady problem.The solution to (1.1.1) is written as

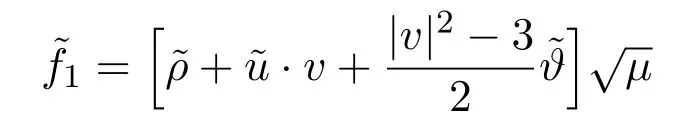

From the choice of (1.2.9) ,we have
Then the equation ofis given by
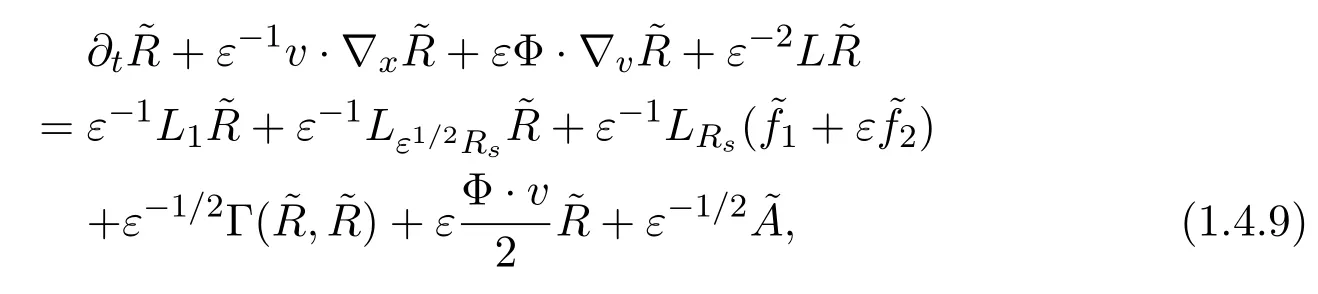

The boundary condition ofis given by

where
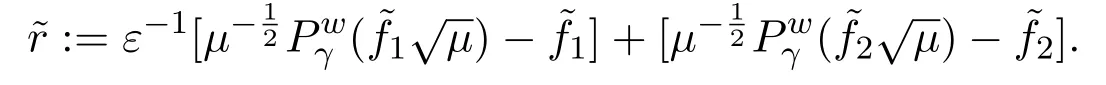
Note that,sinceMwonly depends onϑw,by taking the difference of (1.3.2) ,written for the unsteady and steady solutions respectively,we obtain

We define the energy and the dissipation as

Theorem 1.2We assume the same hypotheses of Theorem1.1.Suppose,andand

and
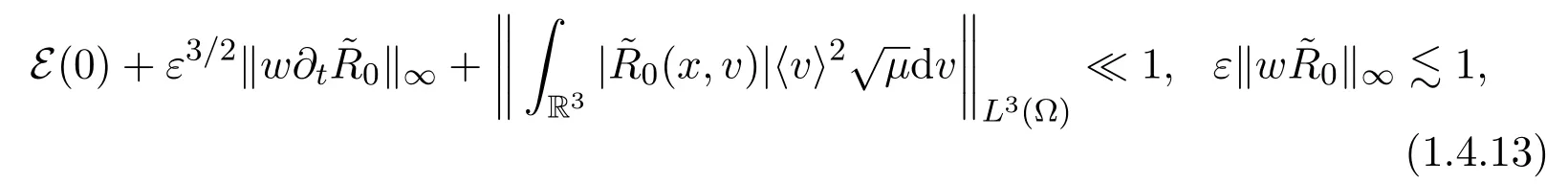
where w (v)=eβ|v|2with 0< β ≪ 1.
Then there exists a unique global solution F≥0 given by (1.4.7) withsolving (1.4.9) and the boundary condition (1.4.11).Here,are given by (1.2.5) and (1.2.8) wheresolves (1.4.8).
Moreover,for some 0<λ≪1,

Here,we recall that the notationmeans.
We remark that such an asymptotical stability implies positivity of steady solutionFs(Section 3.7).Moreover,sincewe conclude that the expansion (1.4.7) is valid in.We use similar ideas as in the steady case,but the analysis is more intricate.
We start with the energy estimates,as the steady case,to get
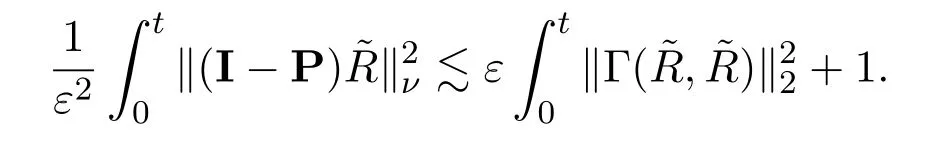
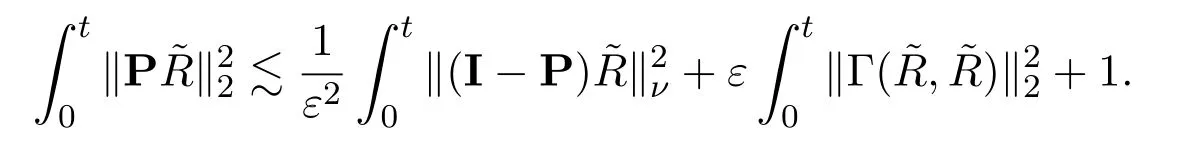
Furthermore,as in the steady case,via a similar extension argument,Lemma 3.3 and Proposition 3.1,we establish a gain of integrability as

Hence,the nonlinearity can be bounded by interpolations:
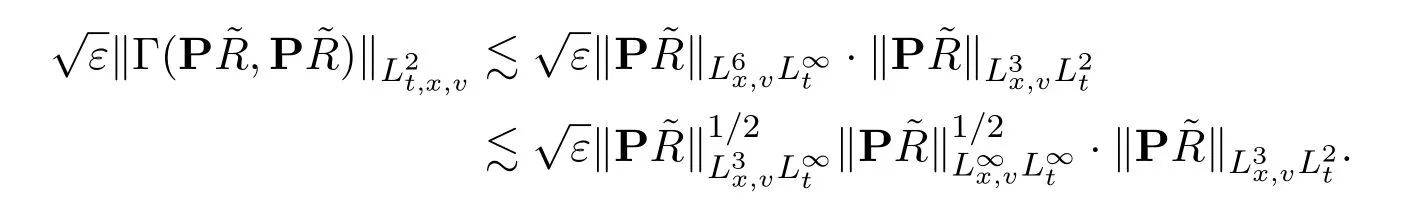

Thanks to the good bound ofε−1∥(I−P)Rs∥2.1 and further by the interpolationL6⊂L2∩L∞,we bound the above by

Similarly to the steady case,by using a double iteration of the Duhamel formula along the characteristics[20],we may bootstrap suchL2estimates to an improvedL∞estimate as
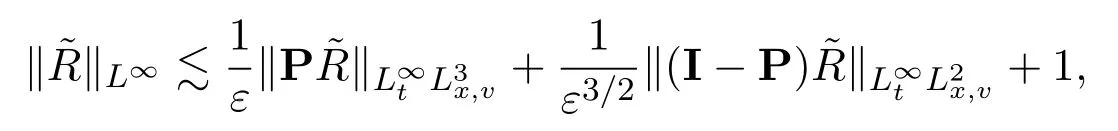
where the dimension isd=3.Clearly,a new difficulty is to estimatewhich is not controllable from (1.4.15).
The key new idea is to repeat energy estimatesestimates for the time derivative

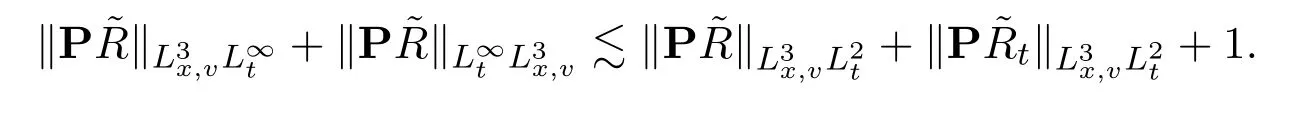
Fortunately,in order to close the estimates,we don’t need to improve,but only need to control the new nonlinear term

which can be exactly closed.
We remark that our method works also for a general 2D domain.Now the gain of integrability is expected as,and it is notcriticaland analysis is much less delicate than the 3D case.
2 Steady Problems
2.1 Domain,Trace,and Green Identity
Assume∂Ω isC3.Then for anyx0∈∂Ω,there exist 0 Assume dist (x,∂Ω)≪1 andx0∈∂Ω such that dist (x,x0)=dist (x,∂Ω).Then there exists anηwhich is a parametrization of∂Ω aroundx0.Clearly On the other hand,if|η(x∥)−x|≪1, Then,by the implicit function theorem,there exists a uniquex∥(x)∈C2satisfying (2.1.1).Moreover, whereη=η(x∥).Then we definex⊥∈C2for dist (x,∂Ω)≪1, Note that dist (x,∂Ω)=|x⊥(x)|if dist (x,∂Ω)≪1. By the compactness of∂Ω,we conclude that if dist (x,∂Ω)<4rfor some 0 Finally we define theC2functionξ:R3→R as where Then Ω={x∈R3:ξ(x)<0}.If|ξ(x)|≪1 thenξ(x)=x⊥(x). We use this new coordinate (2.1.2) to extend Φ on the whole space,and denote Therefore without loss of generality we assume that Φ is defined on the whole space R3. Definition 2.1Assume Φ=Φ (x)∈C1.Consider the steady linear transport equation The equations of the characteristics for (2.1.6) are IfX(τ;t,x,v)∈Ω for allτin betweensandtthen Note that the ODE (2.1.7) is autonomous since Φ is time-independent. Define and Clearly (xb(x,v),vb(x,v))∈γ−and (xf(x,v),vf(x,v))∈γ+. Lemma 2.1For any open subsetΩ⊂R3,B⊂∂Ω,and f∈L1(Ω×R3), and For the proof we refer to Lemma 2.2 in[21].From (2.1.7) ,for∇∈{∇x,∇v}, Next lemma extends the Ukai’s Lemma ([17]) to the case with external fields. Lemma 2.2AssumeΩis an open bounded subset ofR3with∂Ωis C3.We define Then For the proof we refer to Lemma 2.3 in[21]. Lemma 2.3LetΦ∈C1.Assume that f(x,v),g(x,v)∈L2(Ω×R3),{v·∇x+ε2Φ·∇v}f,{v·∇x+ε2Φ·∇v}g∈L2(Ω×R3)and fγ,gγ∈L2(∂Ω×R3).Then ProofIt is easy to check that the proof in Chapter 9 of[17],equation (2.18) ,still holds in the presence ofC1field. In this section,we prove the crucial result on the gain of integrability for velocity averages of the solution to the transport equation. First,we definefδwhich represents either the interior,or the non-grazing parts offnear the boundary. Definition 2.2We define,for (x,v)∈×R3and 0<δ≪1, wheren(x) is defined in (2.1.5). At the boundary (x,v)∈γ=∂Ω×R3, The main goal of this section is the following: Proposition 2.1AssumeΦ=Φ (x)∈C1.Let f(x,v)solve(2.1.6)in the sense of distribution and f(x,v)|γ=fγ(x,v)∈L2(γ).Then where fδis defined in(2.2.1)and(a,b,c)in(1.2.4). Moreover, forwith0<β≪1. Lemma 2.4Let f∈L2(Ω×R3)solve(2.1.6)in the sense of distribution andg∈L2(Ω×R3),and f(x,v)|γ=fγ(x,v)∈L2(γ).Then there exists an,such that.Moreover,in the sense of distributions, where and ProofStep 1Considerfδin (2.2.1).In the sense of distributions on Ω×R3, Note that, This proves the second line of (2.2.8).Since we prove the first line of (2.2.8) directly.The third line of (2.2.8) will be proved in Step 5. Ifv·n(x)≥δ,we takes>0,while ifv·n(x)≤−δthen we takes<0.From (2.1.8) , Fromξ(x)≥0, By the intermediate value theorem,we prove our claim. Step 3We definefE(x,v) for: We check thatfEis well-defined.It suffices to prove the following: The main purpose of this section is to prove the following: Proposition 2.2SupposeΦ∈L∞,g∈L2(Ω×R3),and r∈L2(γ−)such that Then,for sufficiently small ε>0,there exists a unique solution to such that and For the proof we refer to the proof in[21]for the details.As the first step of the proof of Proposition 2.3,we consider the following penalized problem: Lemma 2.6Assume that g∈L2(Ω×R3)and r∈L2(γ−)satisfy(2.3.1).Moreover,letΦ∈L∞(Ω)and λ>0.Then,if ε>0is sufficiently small,the solution to(2.3.5)exists and is unique.Moreover it satisfies the bounds We remark that Lemma 2.6 implies that,forεsufficiently small,the operatorL−1is well-defined and bounded as a map fromL2toL2.For the proof we refer to Lemma 2.10 in[21]. Lemma 2.7For any λ,ε>0,the operator KL−1is compact in L2.Explicitly,if gn∈L2andsupn∥gn∥2<∞then there exist subsequence nksuch that Kfnk→Kf in L2,where fnsolve For the proof we refer to Lemma 2.11 in[21]. Next we prove the essential bound for Pf,wherefsolves We denote Lemma 2.8Assume(2.3.1).Let f be a solution to(2.3.7)in the sense of distribution.Then,for all λ≥0and all θ∈[0,1], and For the proof we refer to Lemma 2.12 in[21]. The main goal of this section is to prove the following lemma. Proposition 2.3Let f satisfy where,forand Then,forwith0<β′≪β, For the proof we refer to the proof in[21]page 27. We define the stochastic cycles for the steady case. Definition 2.3Define,for free variablesvk∈R3,from (2.1.9) The following lemma is a generalized version of Lemma 23 of[32]. Lemma 2.9[32]AssumeΦ=Φ (x)∈C1.For sufficiently large T0>0,there exist constants C1,C2>0,independent of T0,such that for k=C1T05/4, ProofFor 0<δ≪1,we define From|v|>δandxb=x+tbv+O(ε2) (tb)2, For fixedδ>0 andε<ε0≪δ1, Therefore we prove our claim.The rest of proof of (2.4.6) is identical to the proof of Lemma 23 on[32]. Now we are ready to prove the main result of this section: Proof of Proposition 2.3Define,forw(v)=eβ′|v|2, From Lemma 3 of[32],there exists asuch that Then,from (2.4.1) , From (2.4.1) ,on (x,v)∈γ−, The main purpose of this section is to prove Theorem 1.1.We need several estimates before the proof of the main theorem. Lemma 2.10Assume Definition 3.1Assume Φ=Φ (x)∈C1.Consider a unsteady linear transport equation The equations of the characteristics for (3.1.1) are By the uniqueness of ODE where (X,V) is defined in (2.1.7). Define Moreover Lemma 3.1For f∈L1([0,T]×Ω×R3), We refer to the proof of Lemma 3.2 in[21]. Lemma 3.2AssumeΦ∈C1.Assume that f(t,x,v),g(t,x,v)∈L2(R+×Ω×R3),{∂t+ε−1v·∇x+εΦ·∇v}f,{∂t+ε−1v·∇x+εΦ·∇v}g∈L2(R+×Ω×R3)and fγ,gγ∈L2(R+×γ).Then ProofThe proof is from Chapter 9 of[17]with the same modification as Lemma 2.3. Definition 3.2We define,forand for 0<δ≪1, Heren(x) is defined in (2.1.5). We extendfδto the negative time so that we are able to take the time-derivative.Clearly, Note that,at the boundary (x,v)∈γ:=∂Ω×R3, The main goal of this section is the following: Proposition 3.1Assume g∈L2(R+×Ω×R3),f0∈L2(Ω×R3),and fγ∈L2(R+×γ).Let f∈L∞(R+;L2(Ω×R3))solves(3.1.1)in the sense of distribution and satisfies f(t,x,v)=fγ(t,x,v)onR+×γand f(0,x,v)=f0(x,v)onΩ×R3.Then where fδis defined in(3.2.1). Moreover for w=eβ|v|2with0<β≪1. We need several lemmas to prove Proposition 3.1. Lemma 3.3Assume the same hypothesis of Proposition3.1.Then there existanand an extension of fδin(3.2.1),such that Moreover,in the sense of distributions onR×R3×R3, where Clearly,we can conclude the second estimate of (3.2.4). Now we focus on the first estimate of (3.2.4).From Lemma 3.3, From (3.2.15) and (3.2.16) withFinally,from Lemma 3.4 and (3.2.17),(3.2.6) ,we conclude the first estimate in (3.2.4).The proof is completed. The main purpose of this section is to prove the following: Proposition 3.2SupposeΦ=Φ (x)∈C1,g∈L2(R+×Ω×R3),and r∈L2(R+×γ−)such that,for all t>0, Then,for any sufficiently small ε,there exists a unique solution to the problem with f|t=0=f0and f−=Pγf+r onR+× γ−such that Moreover,there is0<λ≪1such that for0≤s≤t, We refer to Proposition 3.8 in[21]. The main goal of this section is to prove the following: Proposition 3.3Let f satisfy Then,for w(v)=eβ′|v|2with0<β′≪β, We define the stochastic cycles for the unsteady case.Note that from (3.1.5), Definition 3.4Define,for free variablesvk∈R3,from (3.1.5) The following lemma is a generalized version of Lemma 23 of[32]. Lemma 3.5[32]AssumeΦ=Φ (x)∈C1.For sufficiently large T0>0,thereexist constants C1,C2>0,independent of T0,such that for, We refer to Lemma 3.12 in[21]for the proof. Now we are ready to prove the main result of this section.We refer to the proof of Proposition 3.10 in[21]in page 80. Lemma 3.6For g(t,x),g(t,x)|t=0=g0(x),for0<δ≪1,and for all T∈[0,∞], Note that this crucial estimate follows essentially by Sobolev imbedding in ProofNote that We prove the first estimate of (3.5.1) :Takingand taking{···}1/2, Now we prove the second estimate of (3.5.1) :From (3.5.2) ,for allt∈[0,T], Taking the integration overxand taking{···}1/p,for allt∈[0,T], Finally takingL∞−norm int∈[0,T], The proof is completed. Lemma 3.7Assume where ai(f)and ai(g)are defined in(2.2.33).Then and ProofFirst we prove (3.5.3).We decompose and|g(t,x,v)|in the same way.We use the same decomposition of (2.5.3) replacing thenorm with thenorm. The first two lines of the RHS of (2.5.3) are bounded by From (2.5.4),(2.5.5),(2.5.6) ,and (2.5.7) ,the third and fourth line of the RHS of (2.5.3) are bounded by The last line of (2.5.3) is bounded by,from, From (3.5.1) , We only need to show∂t[S1f].S1∂tffort≥0.From the Definition of S1f(t,x) in (3.2.3) , Now from the Definition offδin (3.2.1) ,fort≥0 Therefore,fort≥0, All together we prove (3.5.3). Now we prove (3.5.4).Using (3.5.6) ,we again decompose We use the same upper bound as in the proof of (3.5.3) except the first line of RHS in (2.5.3) and the first term of the third and fourth lines of RHS in (2.5.3) : First we focus on the first line of the RHS of (2.5.3).Using the decomposition ofgin (3.5.6) ,these terms are bounded by and From the above estimate and (2.5.4) ,the last two lines of (3.5.7) are bounded by Focus on the first line of (3.5.7).For 0 Now by the change of variables (v,u)↔(v′,u′) for the first term, (v,u)↔(u′,v′) for the third term,the above terms are bounded by Here,for 0 Hence the first line of (3.5.7) is bounded by Therefore,altogether,the first line of RHS of (2.5.3) is bounded by Similarly the first term of the third and fourth lines of RHS in (2.5.3) is bounded as All together we prove (3.5.4). Now we prove (3.5.5).Using the decomposition ofg, The main purpose of this section is to prove Theorem 1.2.To that we need the following: Moreover, ProofFrom (1.3.3),(1.3.4) ,and our choice (1.2.9) , Then from (.1) we conclude (3.6.1). From (1.2.14) and (1.2.9) , By the standard Sobolev embedding and the trace theorem,we prove (3.6.4).The proof is completed. Proof of Theorem 1.2For the construction of the solution and the energy estimate,we considersolving,forℓ∈N, Note that Proposition 3.2 guarantees the solvability of such linear problems (3.6.6) and (3.6.7). Note that from the assumption (1.4.12),(.1) ,and (3.6.1) , For 0<η0≪1 and 0<η1<∞,we assume (induction hypothesis) that In this section,we prove the non-negativity ofFsin the main theorem.The proof is based on the asymptotical stability ofFs(Proposition 3.1) and the non-negativity of unsteady solution. Proof of the non-negativity ofF(t,x,v) in Theorem 1.2 andFs(x,v) in Theorem 1.1 We use the positivity-preserving sequence as in[20,32].SetF0(t,x,v)=F0(x,v)≥0 and forℓ≥0 Appendix A Basic Estimates of the Fluid Equations In this Appendix,to simplify the formulas,we set v=1 andκ=1,since they do not play any role in the estimates. Lemma A.1Let(us,ϑs)be the H2−solution to the steady INSF(1.4.1).Assume(1.4.4).Then If we further assumeandthen. Lemma A.2Let(u,ϑ,p)be Hksolution to(1.2.7).Set,,wheresolves(1.4.8).Assume Then,for any k≥0and for0<λ≪1, whenever the RHS is finite for some polynomial P. Moreover,for some0<λ≪1and polynomial P0with P0(s)=O(s), whenever the RHS of(A.1)is finite and Furthermore,


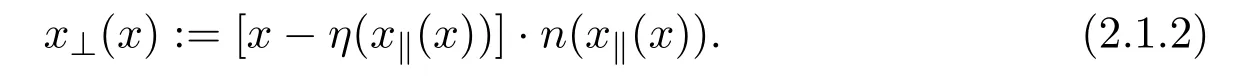
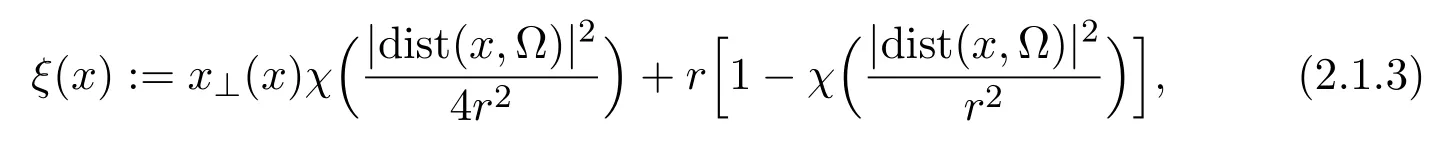

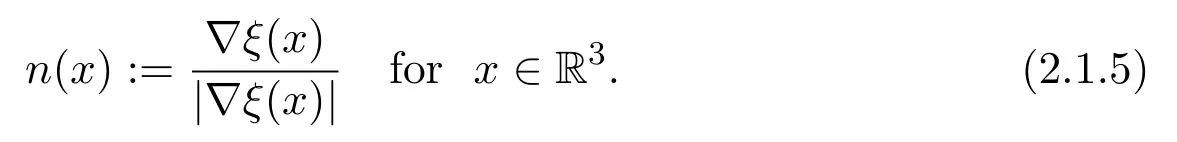
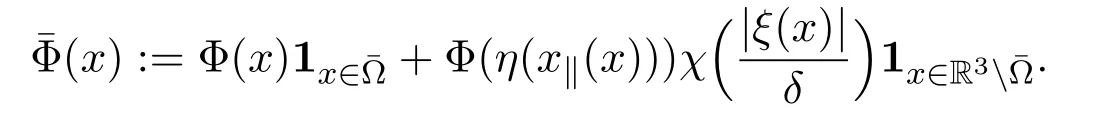
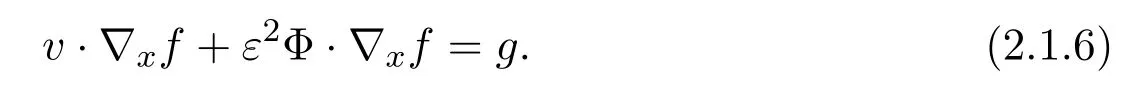






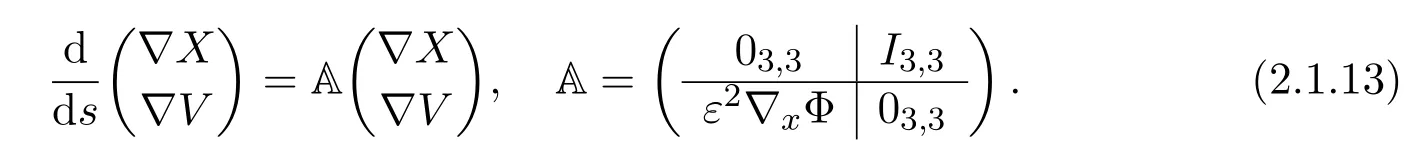
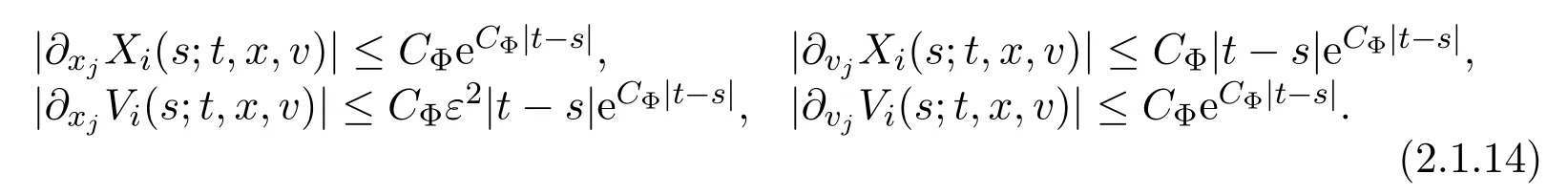

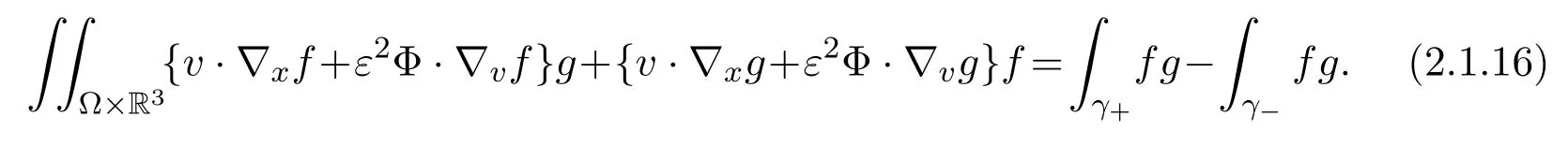
2.2 Gain of Integrability: Estimate
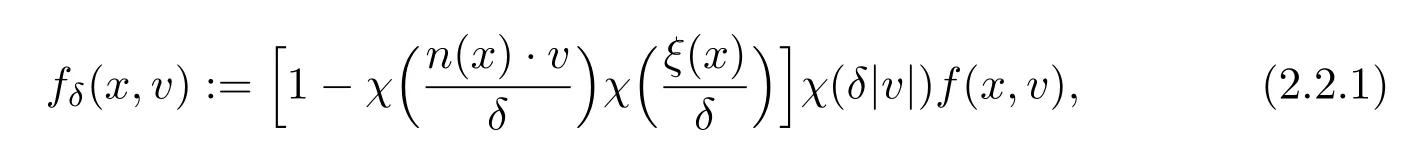



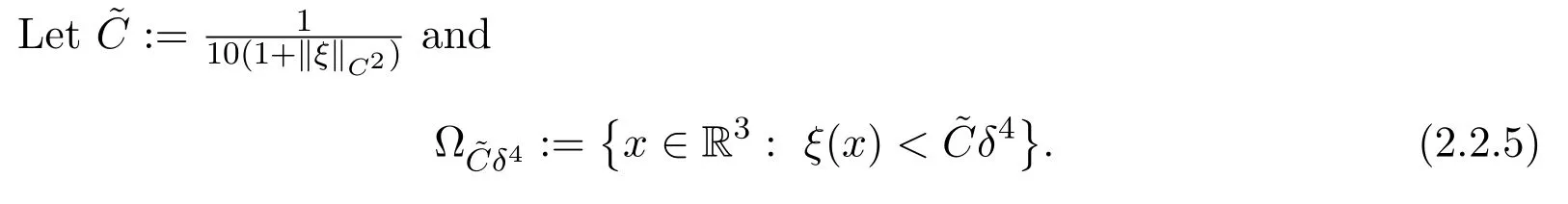
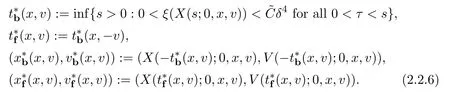


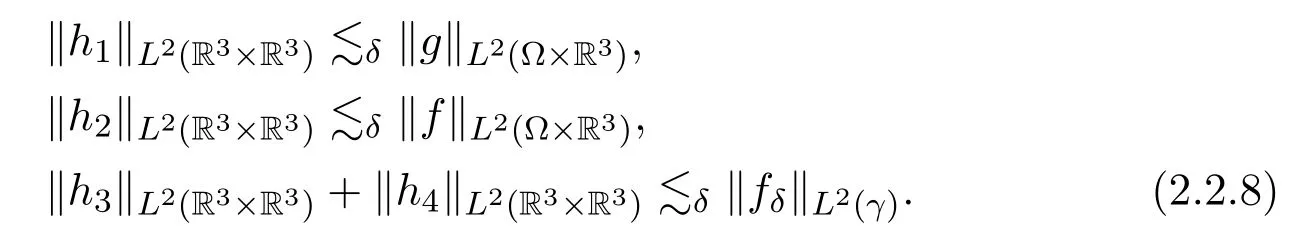
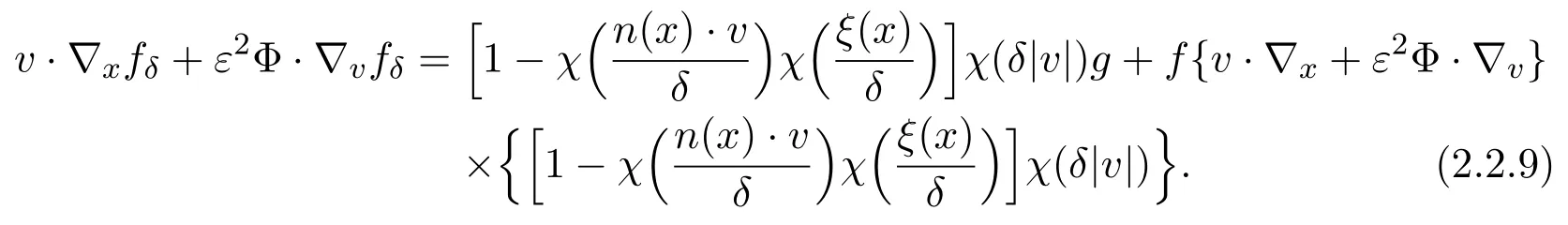


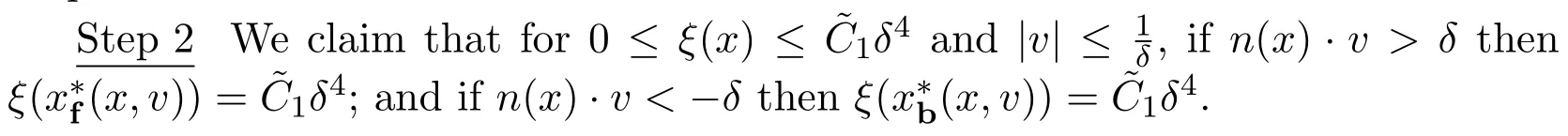

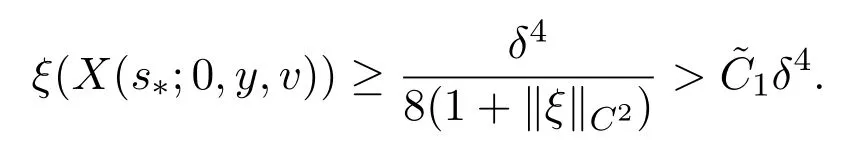






2.3 Steady L2− Coercivity



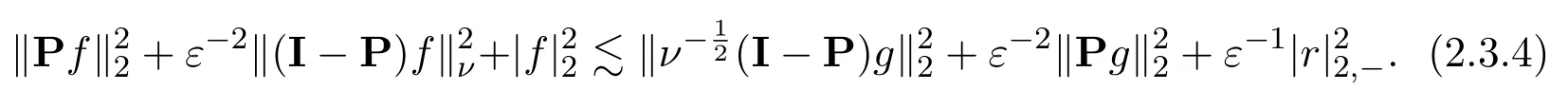
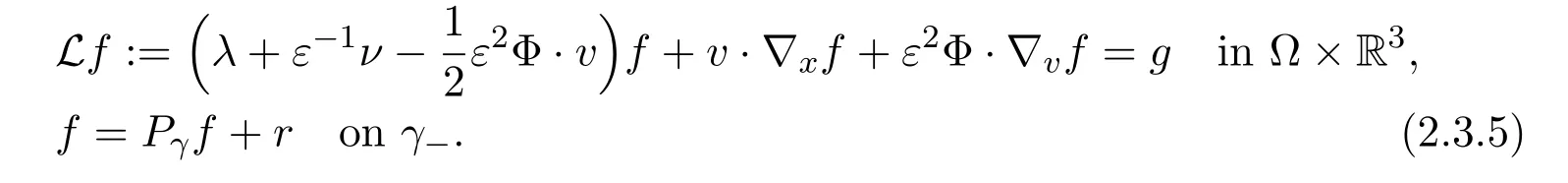



2.4 L∞ Estimate


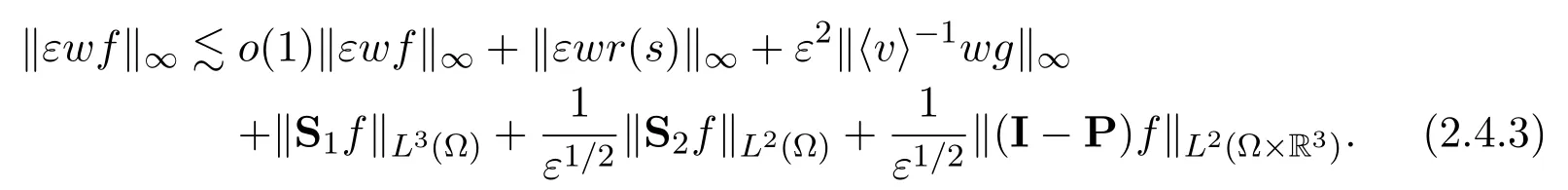
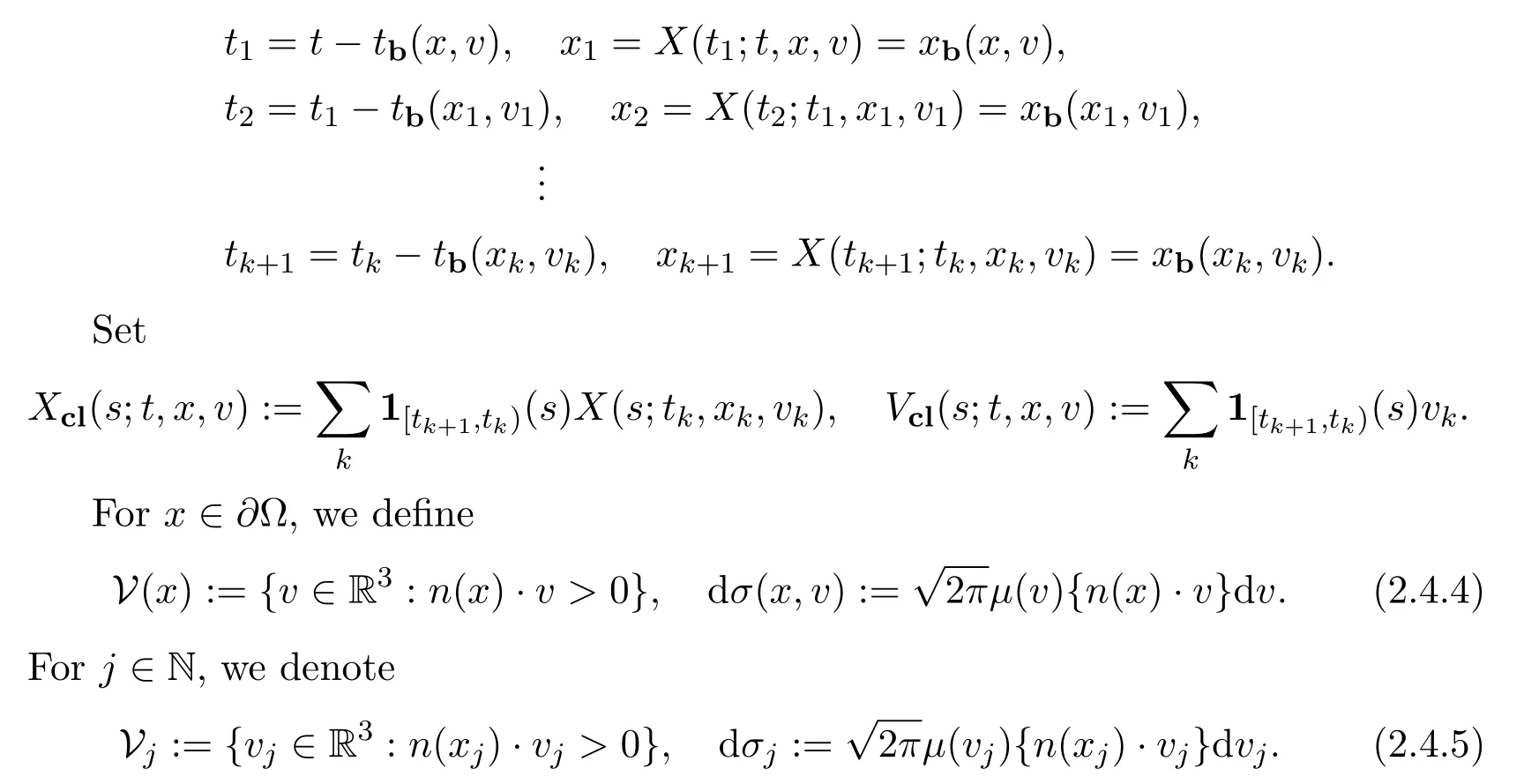



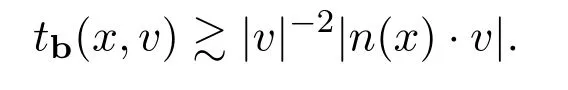






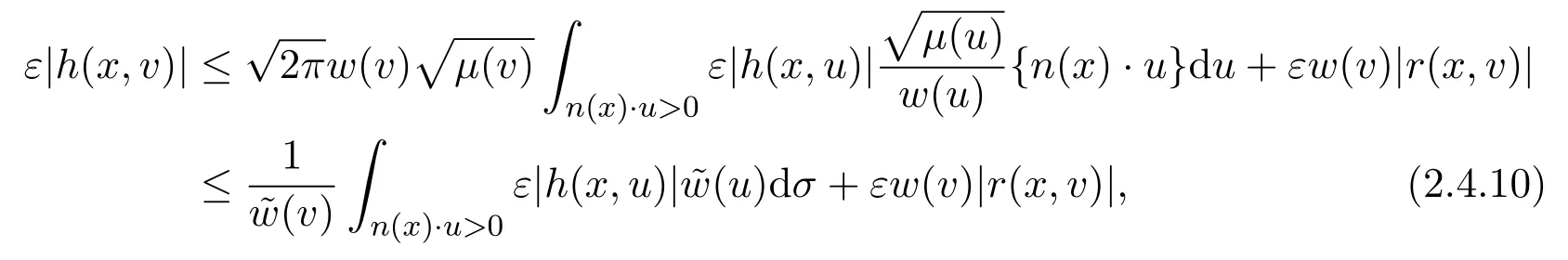




2.5 Validity of the Steady Problem






3 Unsteady Problems
3.1 Trace and Green’s Identity




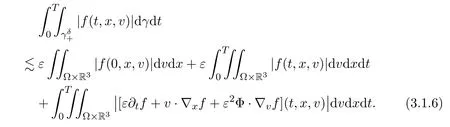
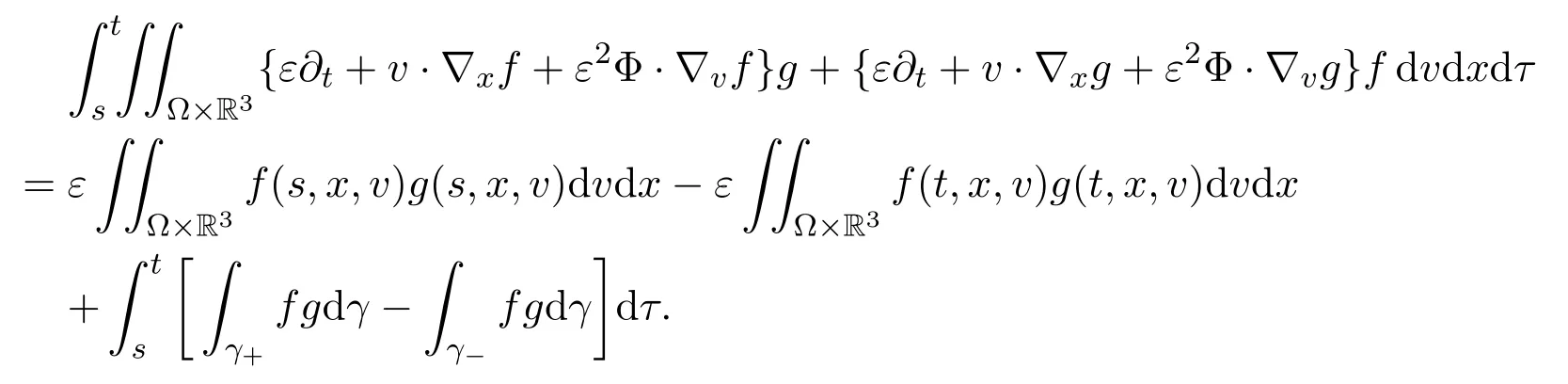
3.2 Gain of Integrability: Estimate
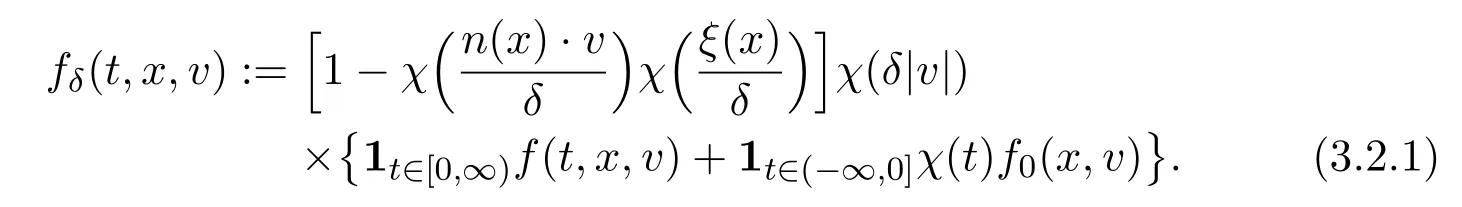


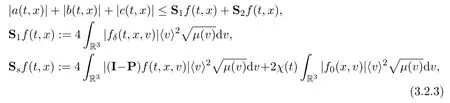
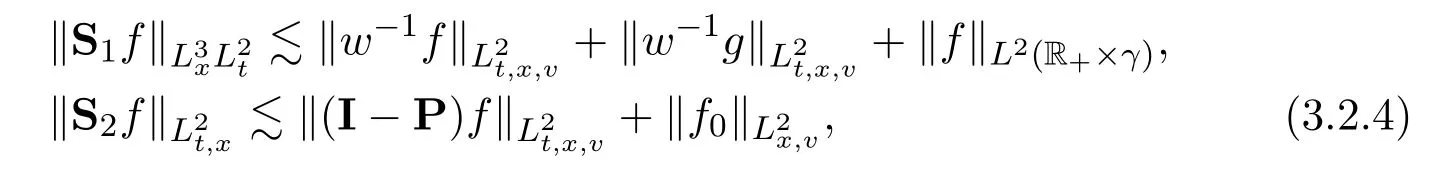











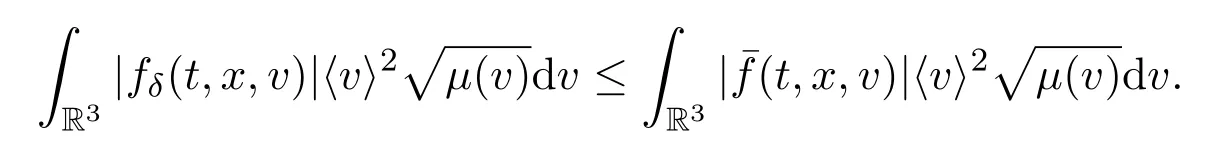
3.3 Unsteady L2− Coercivity Estimate
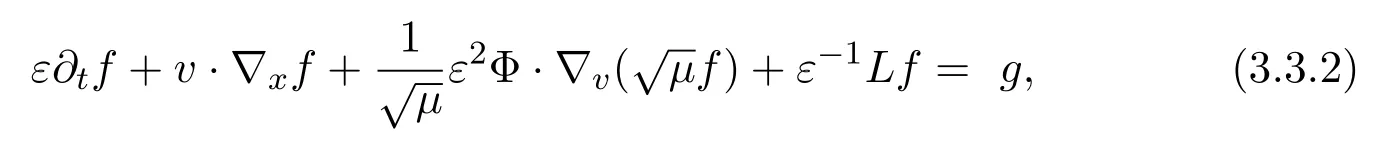


3.4 L∞ Estimate
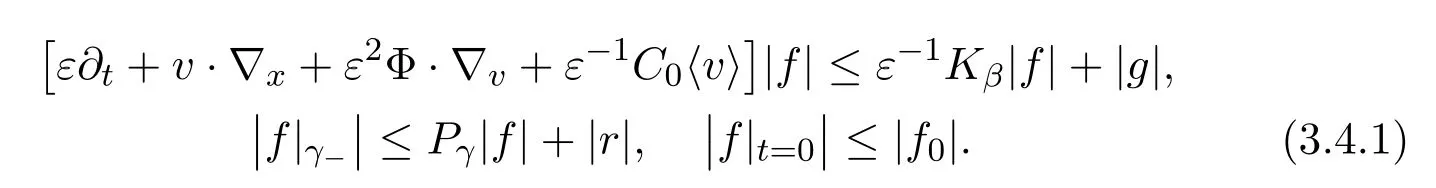

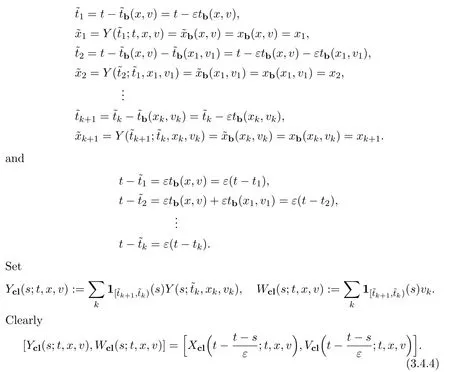
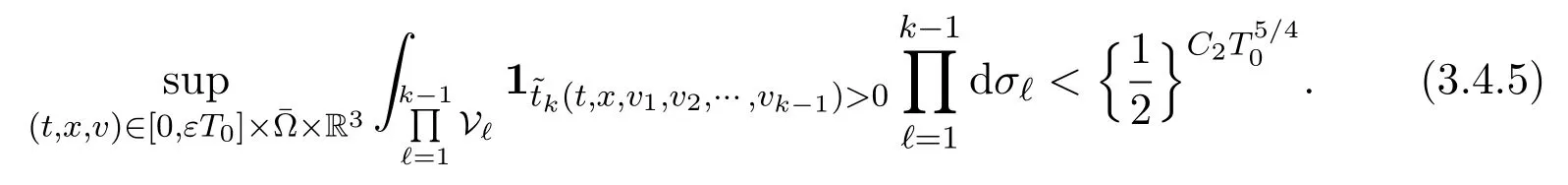

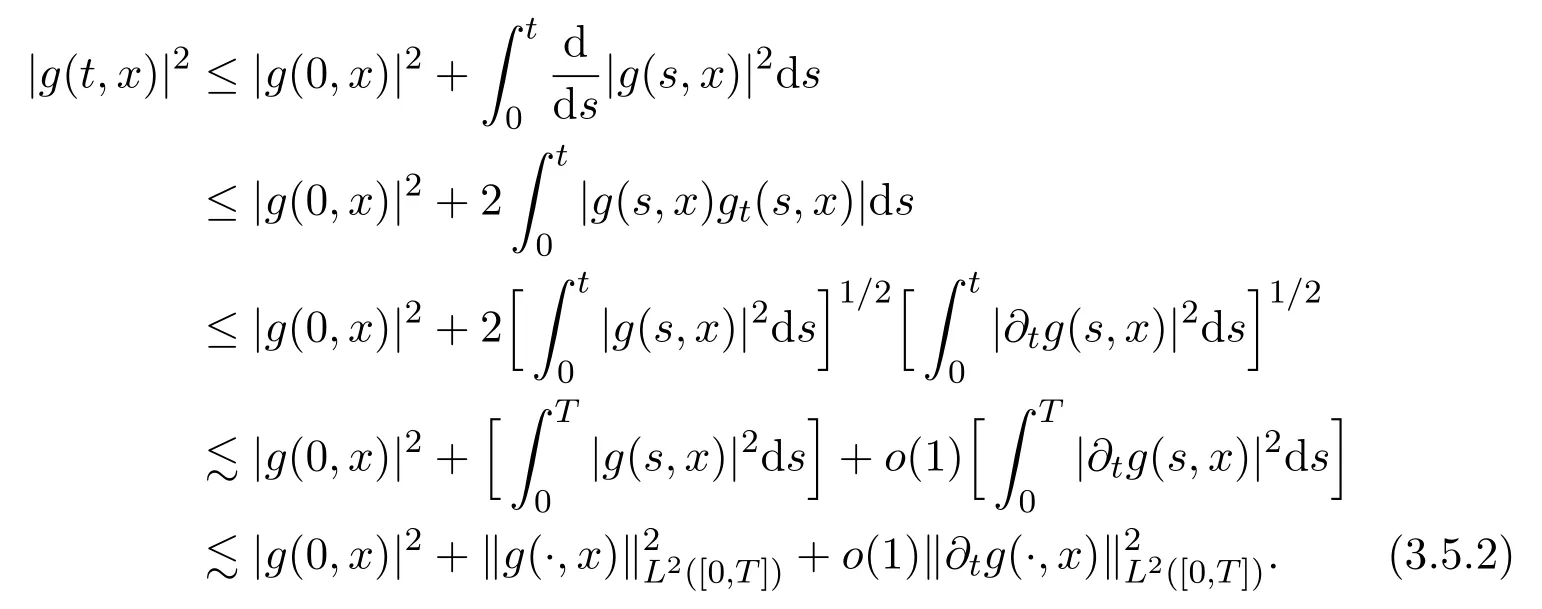



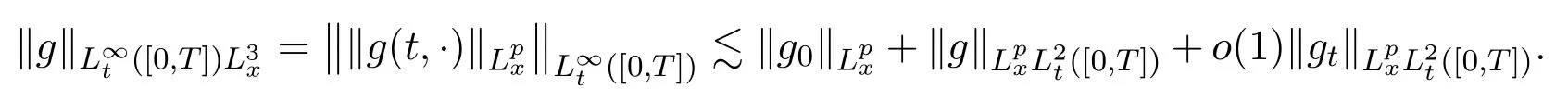
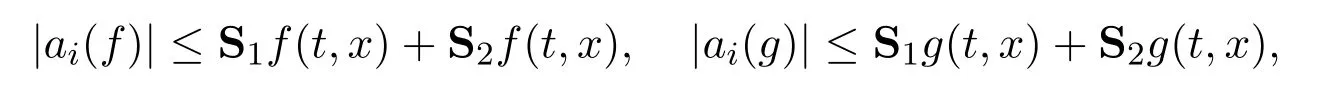
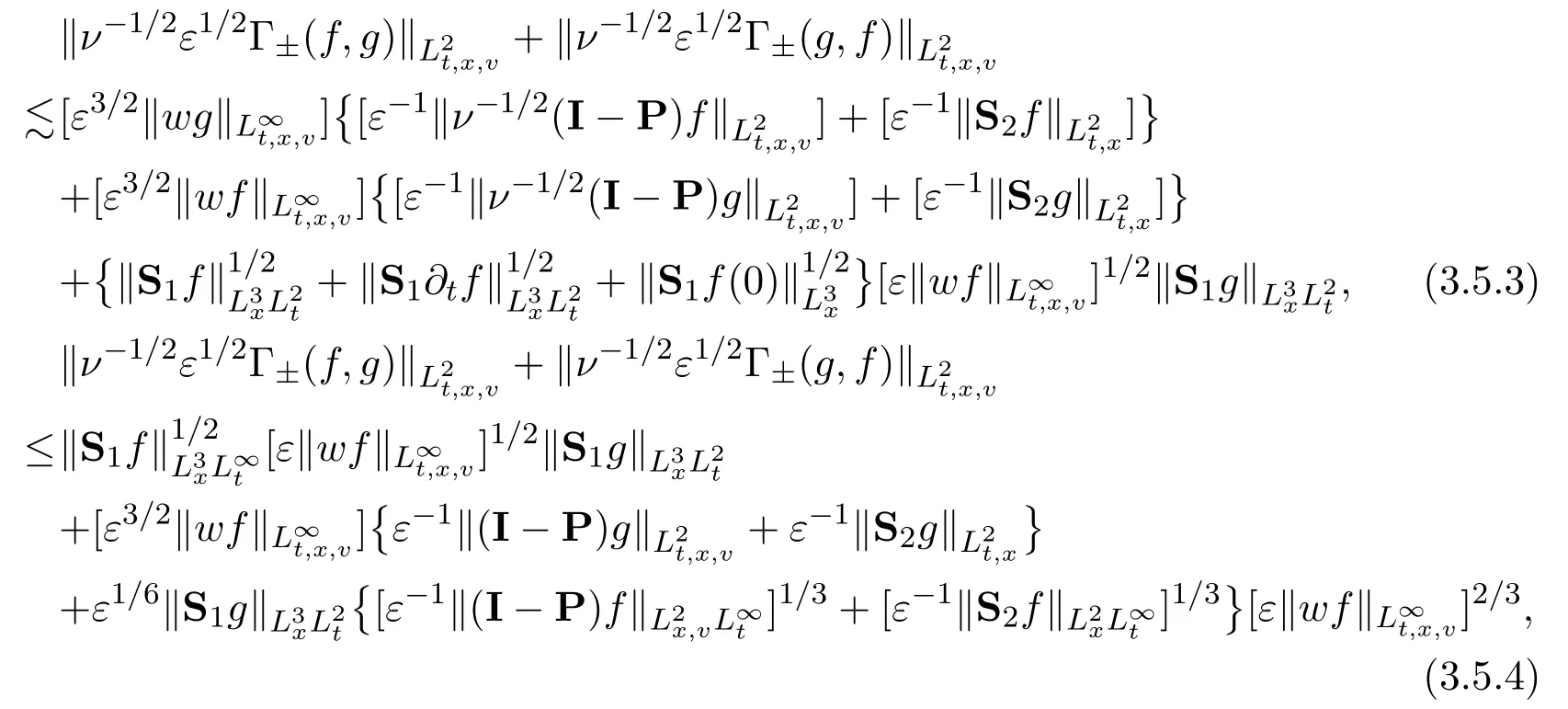
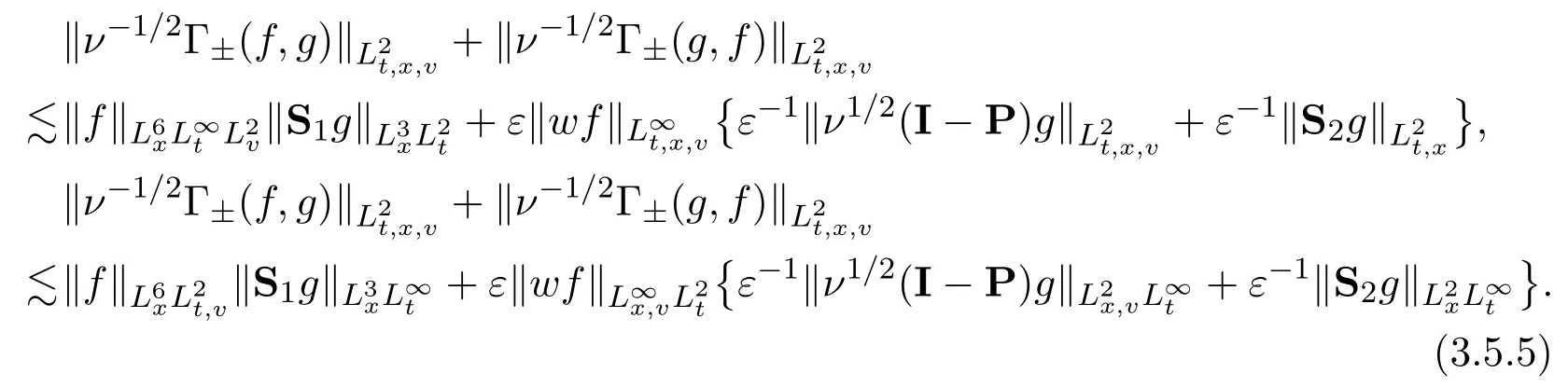



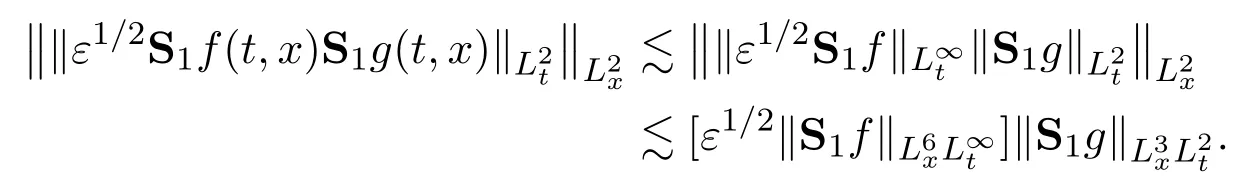

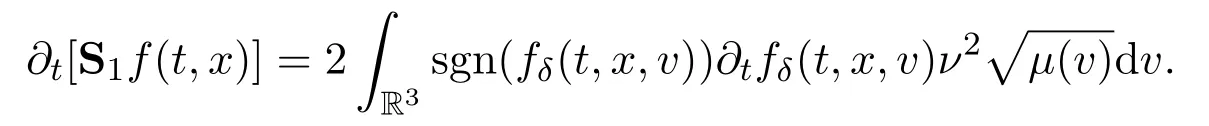
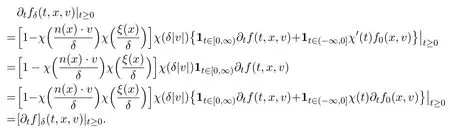
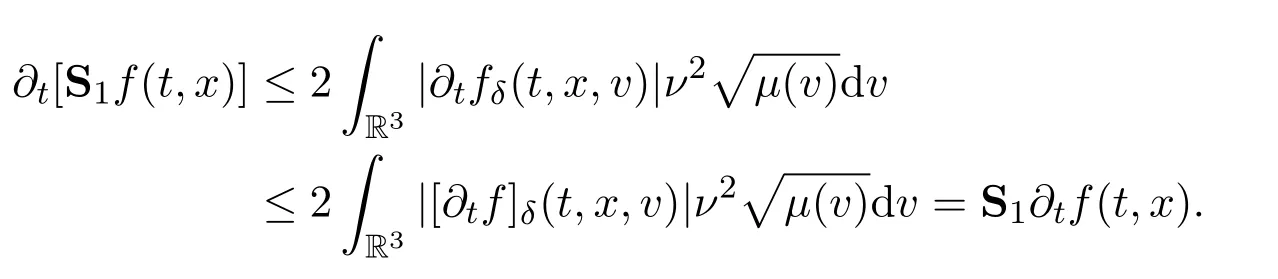




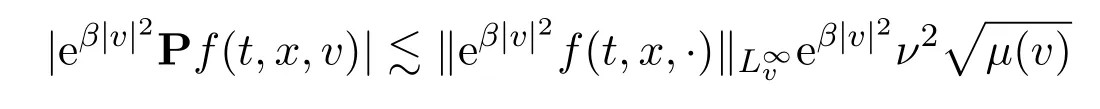
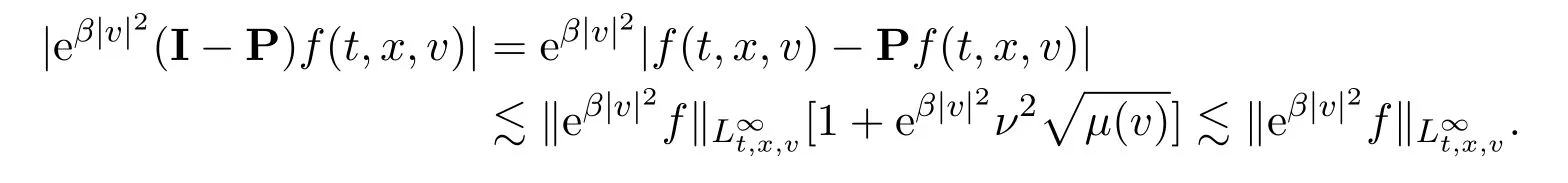
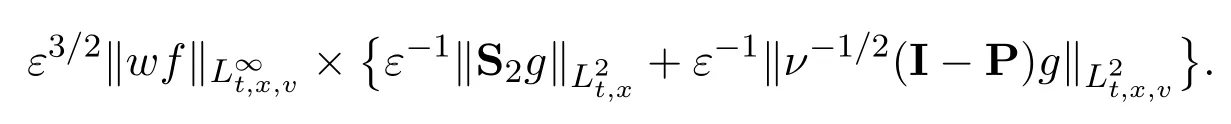
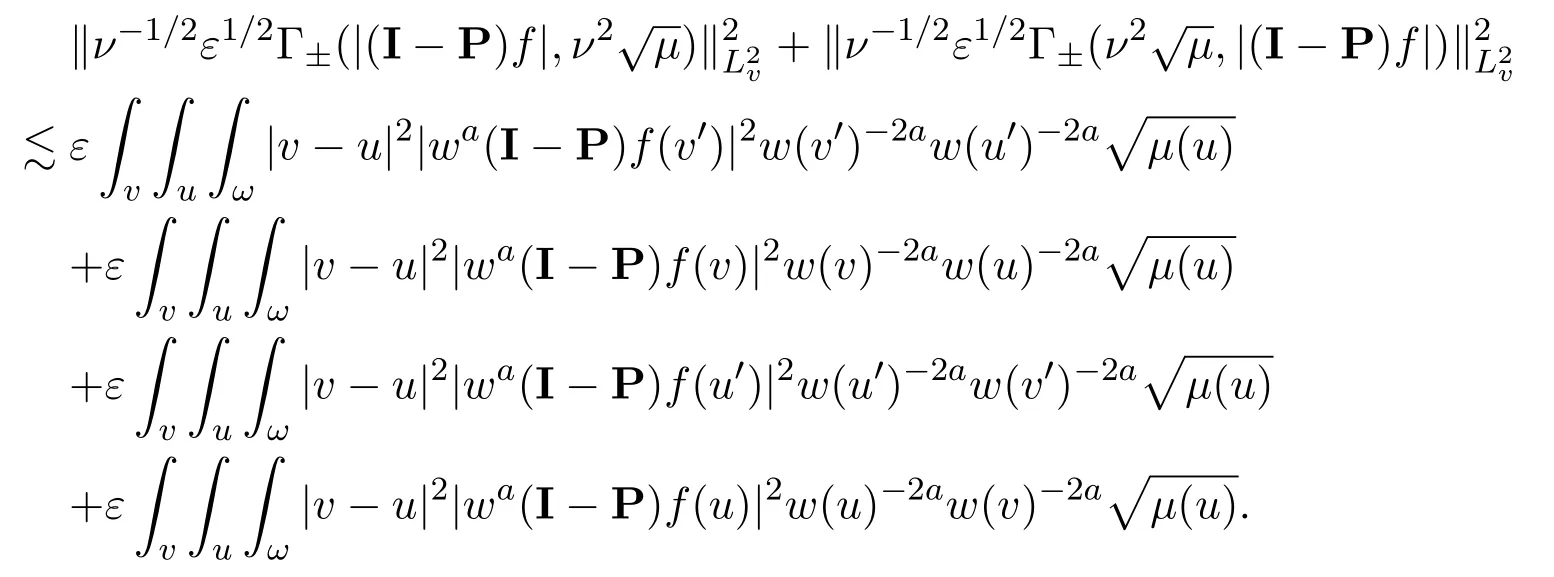

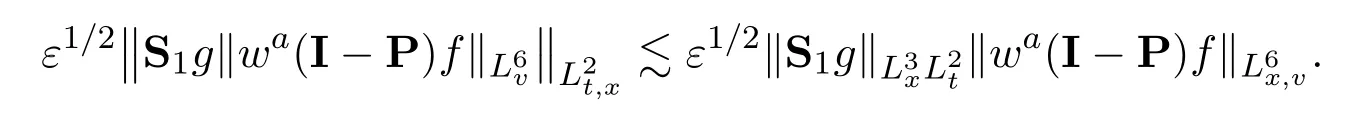
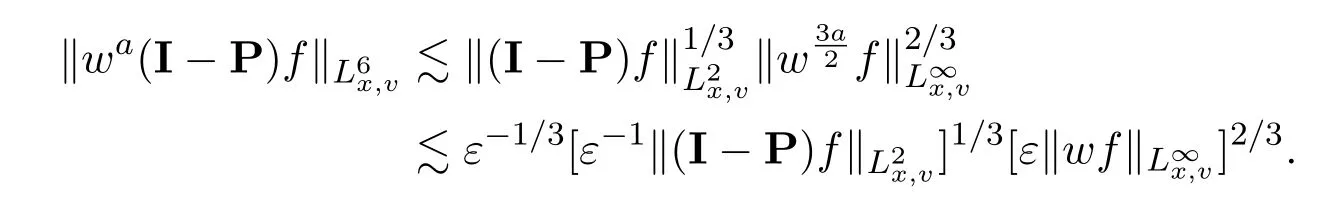




3.6 Global-in-Time Validity
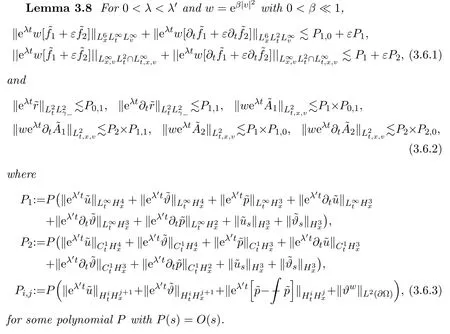
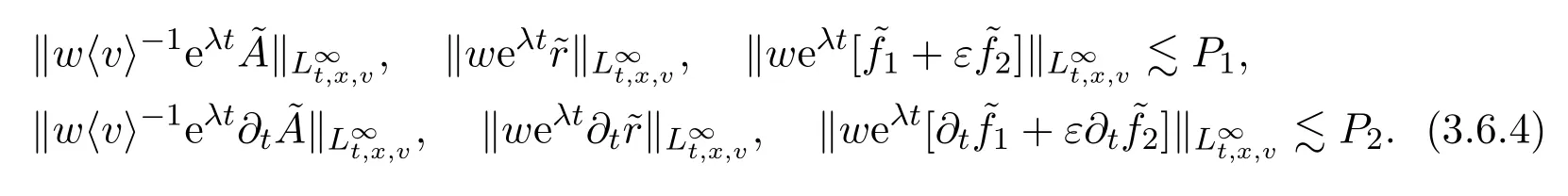


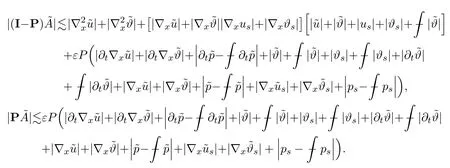
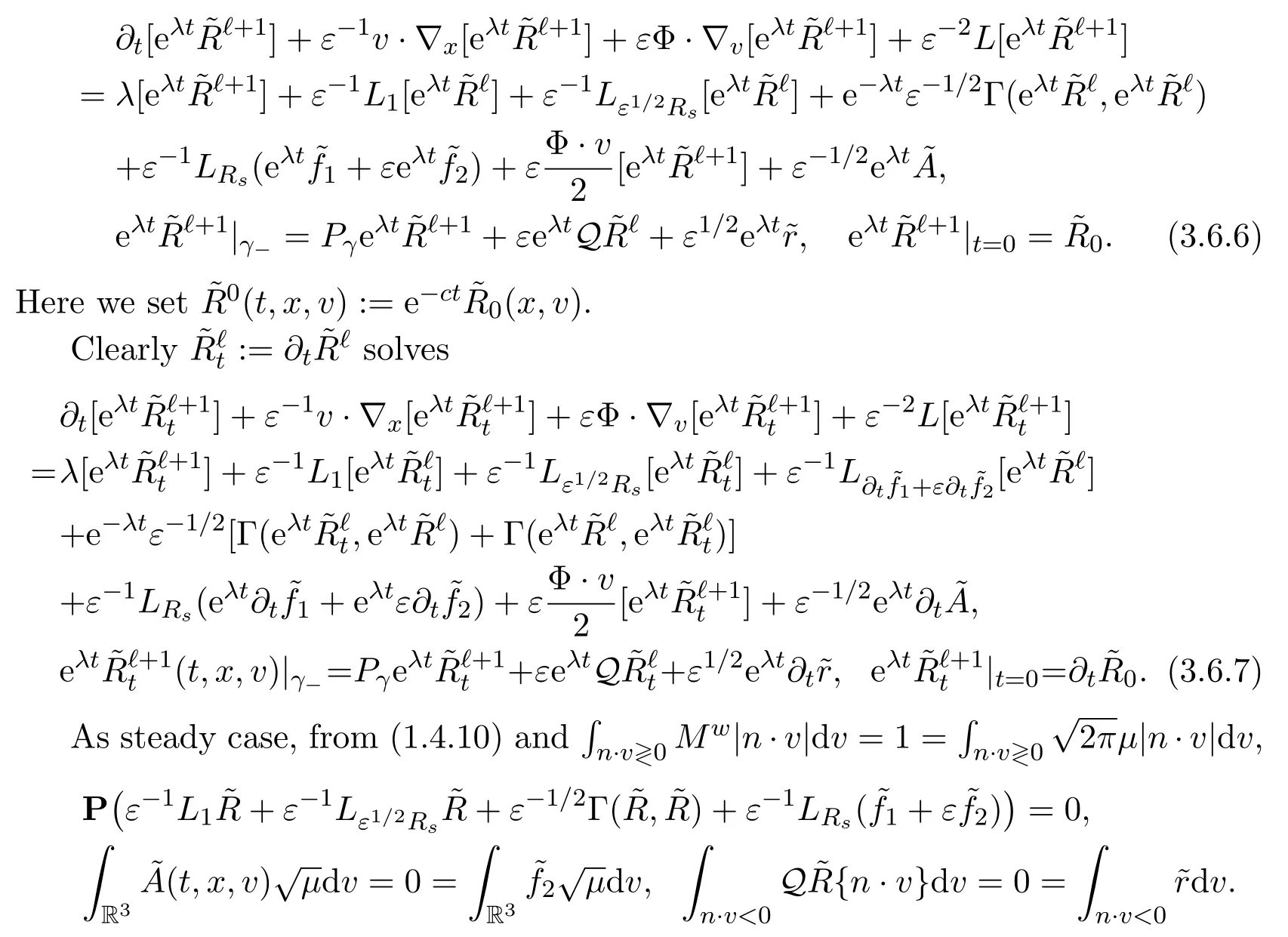






3.7 Positivity of Solutions