A NOTE ON CLINE’S FORMULA FOR TWO SUBCLASSES OF GENERALIZED DRAZIN INVERSES∗†

Kai Yan

(College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,Fujian,PR China)

Abstract

Keywords generalized Drazin inverse;extended g-Drazin inverse;generalized strong Drazin inverse;Cline’s formula

1 Introduction and preliminaries

LetAbe a Banach algebra with identity.Fora∈A,the notationsσ(a) ,accσ(a) andr(a) denote the spectrum,accumulated spectral points and the spectral radius ofa,respectively.The sets of all invertible elements,nilpotent elements and quasinilpotent elements ofAare denoted byAinv,AnilandAqnil,respectively.Set

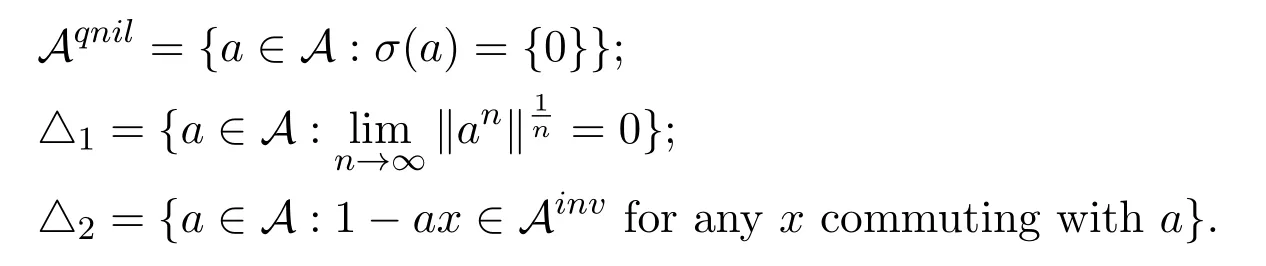
Lemma 1.1[5]Let A be a Banach algebra with identity.Then Aqnil=△1=△2.

In 1958,Drazin[3]introduced a new notion of invertibility,which is now commonly known as Drazin invertibility,in semigroup.The Drazin inverse plays a significant role in operator theory,singular Differential equations,Markov chains,etc.,see[1].Recall that an elementa∈Ais Drazin invertible if there exists an elementx∈Asuch thatax=xa,xax=xanda−a2x∈Anil.The nilpotent index ofa−a2xis called the Drazin index ofa.We useaDto denote the Drazin inverses ofa.By extending nilpotent element to quasinilpotent element,Koliha[6]introduced a concept of generalized Drazin invertibility in Banach algebras.

Definition 1.1[6]An elementa∈Ais generalized Drazin invertible if there exists an elementx∈Asuch that

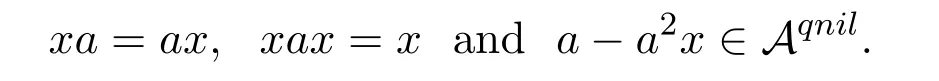
In this case,xis called the generalized Drazin inverse ofaand is denoted byagD.

If suchxexists,it is unique.The notationAgDdenotes the set of all generalized Drazin invertible elements inA.It is easy to see thatAqnil⊆AgD,because the generalized Drazin inverse of a quasinilpotent element is zero.The generalized Drazin spectrum is defined by

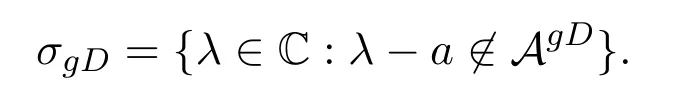
In[6],Koliha proved thata∈AgDif and only if 0accσ(a).This impliesσgD(a)=accσ(a).In order to generalize the ideal of Koliha,Mosi[9]introduced a new type of outer generalized inverse.

Definition 1.2[9]An elementa∈Ais extended g-Drazin invertible (or eg-Drazin invertible) if there exists an elementx∈Asuch that

In this case,xis called the extended g-Drazin inverse ofaand is designated byaed.

Different from generalized Drazin inverse,the eg-Drazin inverse is not unique,see[9,Example 2.1].However,the existence of extended g-Drazin inverse and generalized Drazin inverse are equivalent.We useAedto denote the set of all generalized Drazin invertible elements inA.By Lemma 1.2,we haveAed=AgD.

Lemma 1.2[8]Let a∈A.The following statements are equivalent:

(1)a is eg-Drazin invertible;

(2)a is generalized Drazin invertible;

(3)0σgD(a) (=accσ(a));

(4)there exists an idempotent q∈A such that

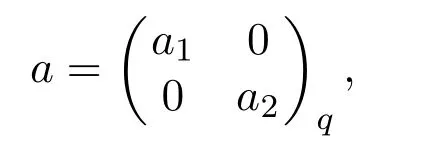
where a1∈(qAa)−1and a2∈AgD.

Motivated by the strong nil-cleanness,the notion of strong Drazin inverse in a ring was introduced and studied in[11]. By extending nilpotent element to quasinilpotent element,the generalized strong Drazin inverse was introduced in Banach algebras.More interesting properties of strong Drazin inverse and generalized strong Drazin inverse can be found in recent paper[8].

Definition 1.3[8]An elementa∈Ais generalized strong Drazin invertible if there exists an elementx∈Asuch that

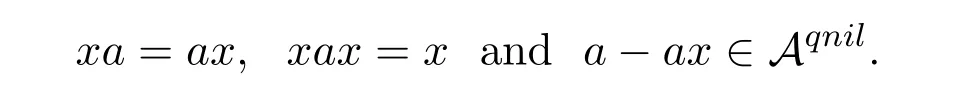
In this case,xis called the generalized strong Drazin inverse ofaand is denoted byagsD.

The notationAgsDdenotes the set of all generalized strong Drazin invertible elements inA.Note thatAgsD⊂AgD.In fact,suppose thata∈AgsDandx=agsD.Thena−a2x=(a−ax) (1−ax) ,so that

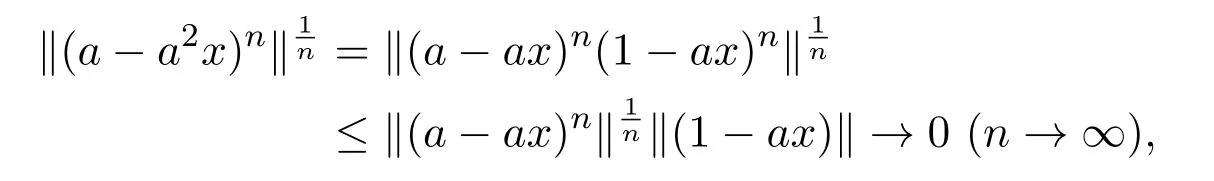
whencex∈Aqnil.Thusx=agD,that isa∈AgD.

The Jacobson’s lemma states that,if 1−acis invertible,so is 1−ca.In a Banach algebraA,Jacobson’s lemma impliesσ(ac){0}=σ(ca){0},and so

We refer the readers to[7,13,16]for some recent research of Jacobson’s lemma.Corresponding to the Jacobson’s lemma,Cline[2]found a fundamental relation between the Drazin inverses ofacand thatca,that is (ac)D=a(ca)Dc.This result is known as Cline’s formula,and its generalizations for different kinds of generalized inverses were presented in[4]and[12].In[15],Zeng et al.established a formula between the Drazin (resp.generalized Drazin) inverses ofacand that ofbdunder the conditionsacd=dbdanddba=aca.Recently,the authors[14]introduced new conditionsbac=bdbandcdb=cac,and investigated the Drazin (resp.generalized Drazin) inverses ofacand that ofbdunder these new conditions.In this paper,we mainly study this new extension of Cline’s formula for two subclasses of generalized Drazin inverses (extended g-Drazin inverses and generalized strong Drazin inverses) in Banach algebras.The connections between the Cline’s formula of these two subclasses of generalized Drazin inverses are given.

2 New Extensions of Cline’s Formula for Two Classes of Generalized Inverses

In this section,some new extensions of Cline’s formula for generalized Drazin inverses,extended g-Drazin inverses and generalized strong Drazin inverses are given.We firstly consider the extended g-Drazin invertible case.

Theorem 2.1Let a,b,c,d∈A satisfy bac=bdb and cdb=cac.Then

In this case,

ProofSuppose thatbd∈Aedandx=(bd)ed.Sety=acdx3b.Then we have

and can conclude the following three conditions:

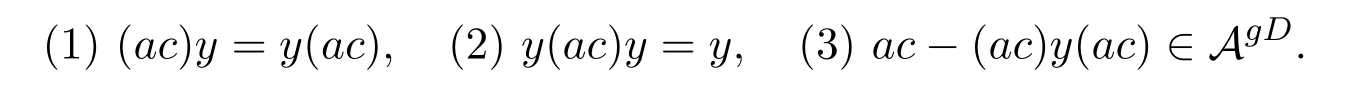
(1) From

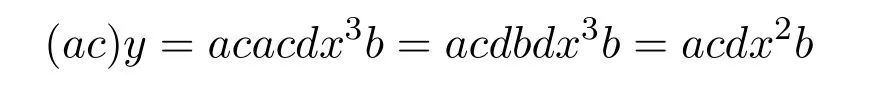
and

it follows that (ac)y=y(ac).

(2)

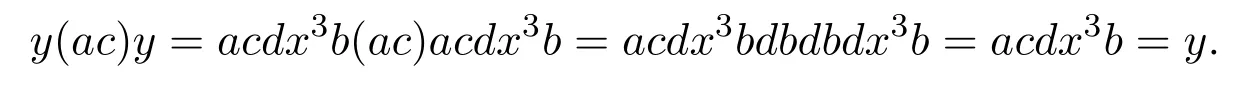
(3) Let

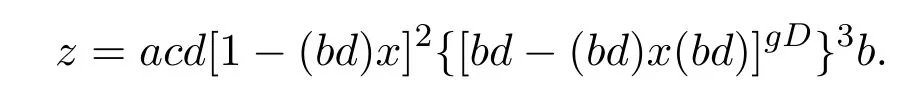
We will show thatz=[ac−(ac)y(ac) ]gD.First,since

there are

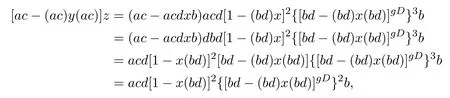
and

Hence[ac−(ac)y(ac) ]z=z[ac−(ac)y(ac) ].Note that

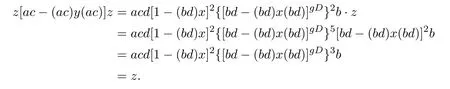
Finally,it only needs to prove that

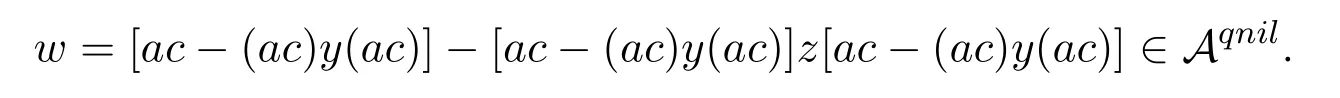
Here

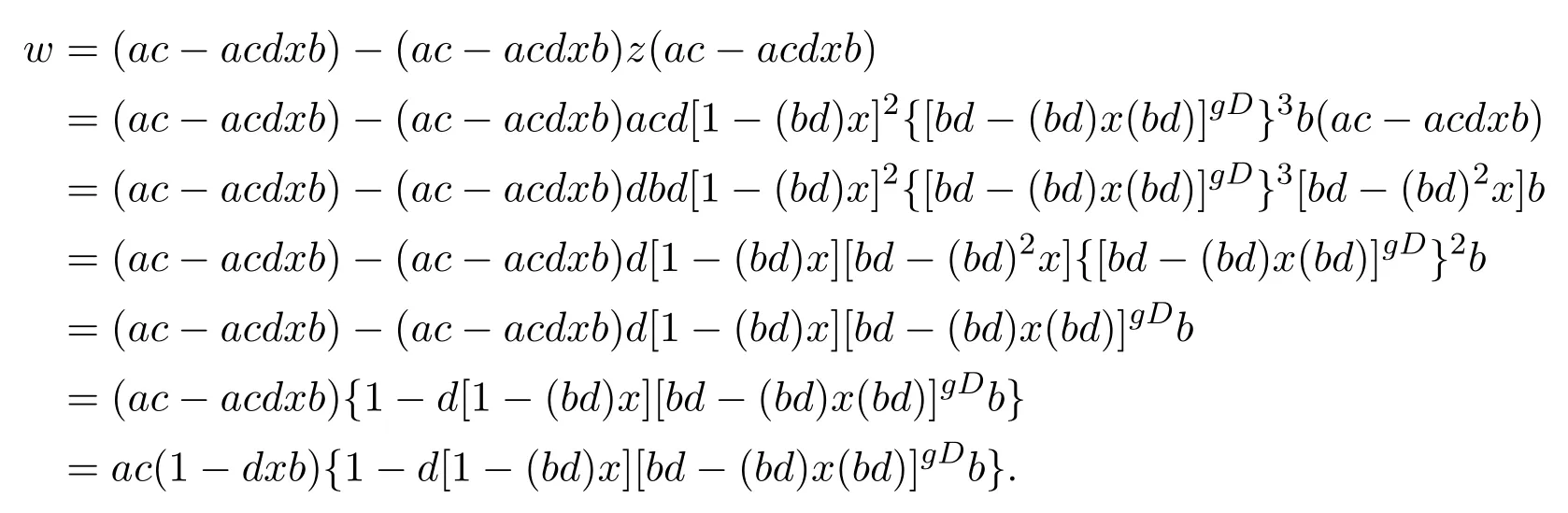
Since 1−(bd)xand 1−bd[1−(bd)x]2[bd−(bd)x(bd) ]gDare idempotent elements inA,we have

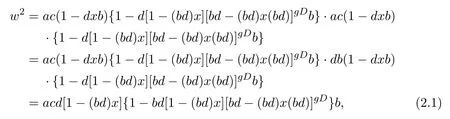
and so

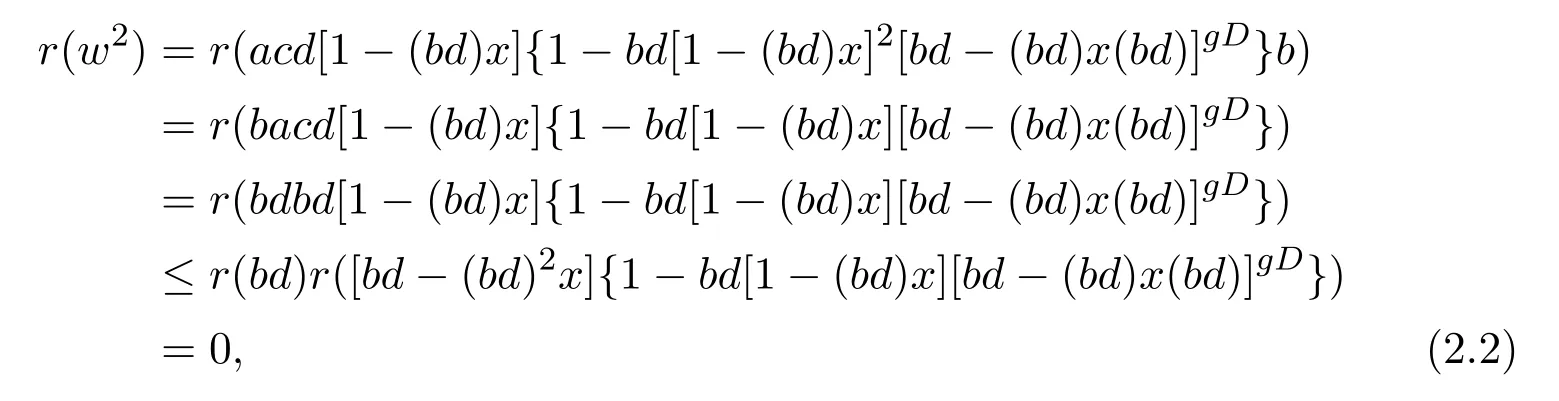
the second equality of (2.1) holds due to equation (1.1) in Section 1,and inequality (2.2) holds by[10,P20,Theorem 11].Thusr2(w)=r(w2)=0.Hencer(w)=0,that isw∈Aqnil.We now get thatac−(ac)y(ac)∈AgDand

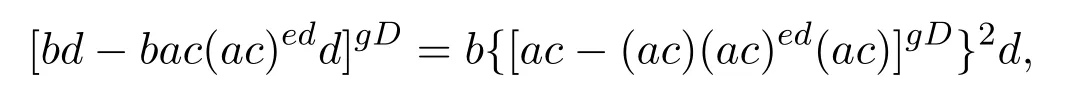
one can verifyy=(bd)edsimilarly to the previous part.The proof is completed.

Remark 2.1In[9],Mosiproved that

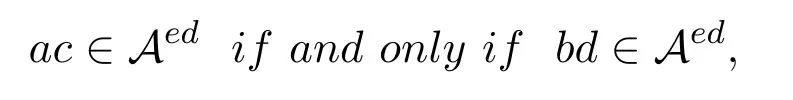
under the conditionsacd=dbdanddba=aca,which are different from the conditions of Theorem 2.1.Moreover,the relations between (ac)edand (bd)edare provided.However,from the proof of Theorem 2.1,we observe a little typo in equality (2) of[9,Theorem 4].Setx=(bd)edand

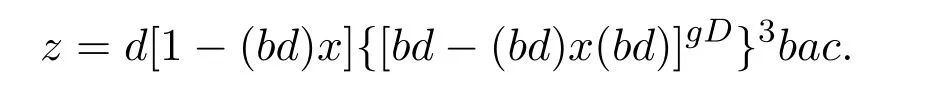
Then

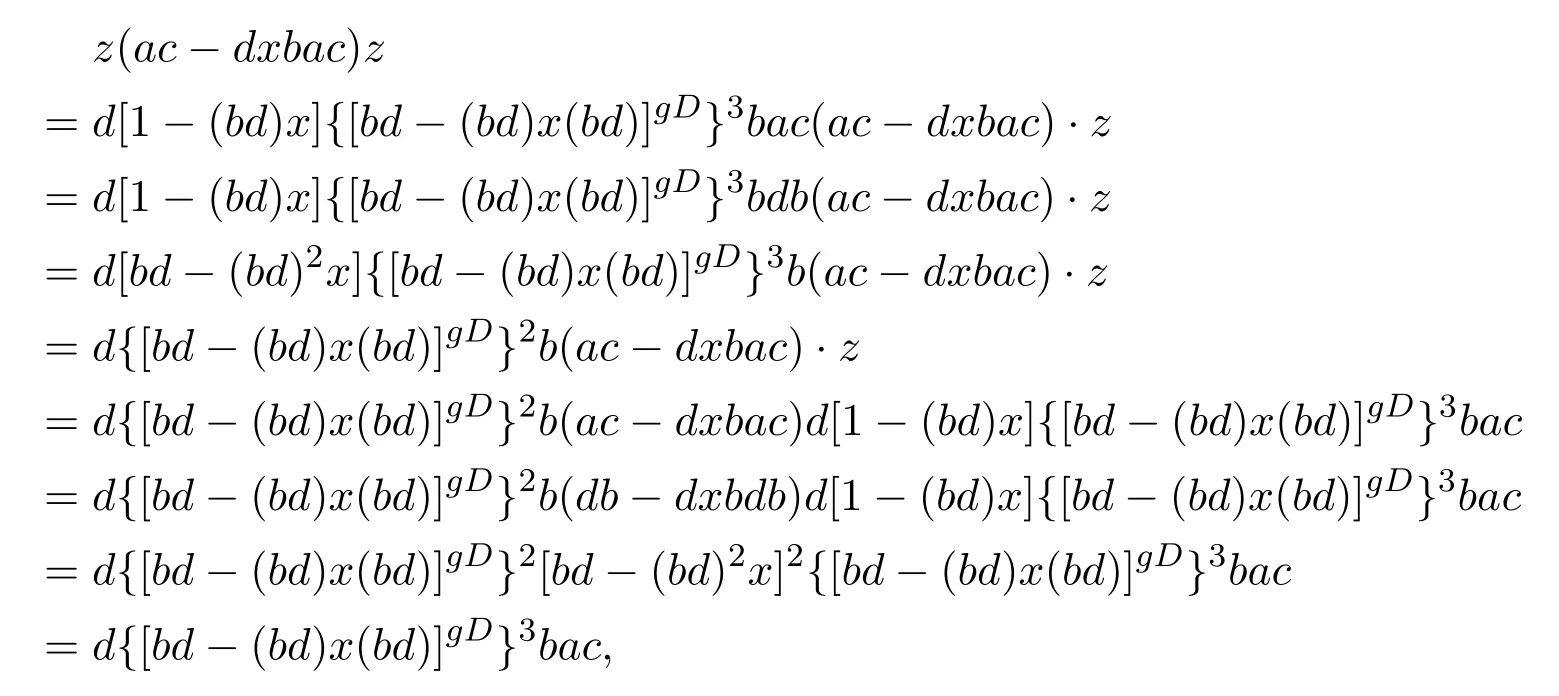
so thatz(ac−dxbac)z̸z,hencez̸[ (1−dxb)ac]gD.In fact,the equality (2) of[9,Theorem 4]should be changed to

In[14],the authors studied the relation between the generalized Drazin inverse ofacand that ofbd,under the conditionsbac=bdbandcdb=cac,in rings.Here,we provide a different approach to study this result in Banach algebras.

Corollary 2.1Let a,b,c,d∈A satisfy bac=bdb and cdb=cac.Then

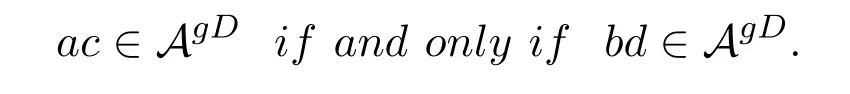
In this case,

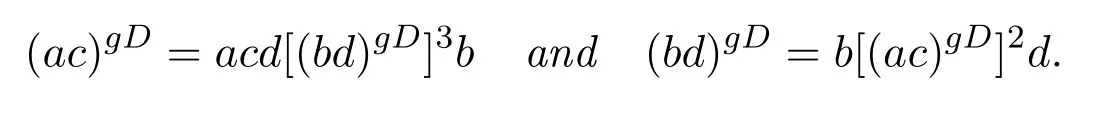
ProofBy Lemma 1.2 and Theorem 2.1,we immediately deduce the conclusion.

Lemma 2.1Let a,b,c,d∈A satisfy bac=bdb and cdb=cac.Then

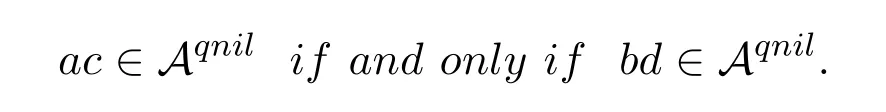
ProofSuppose thatac∈Aqnil,that is.Then

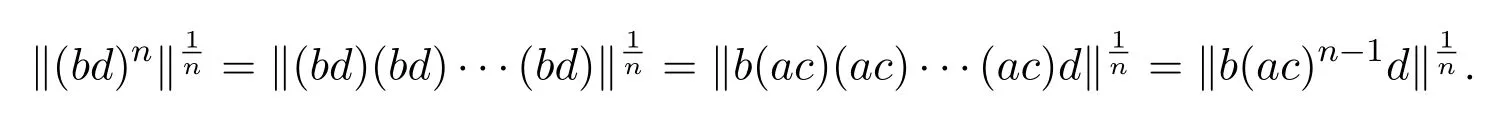
Since

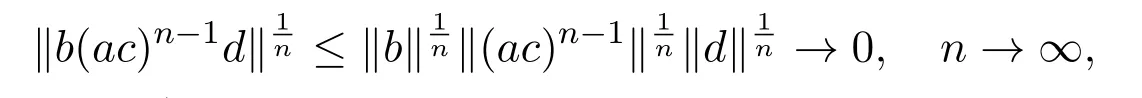
It is not hard to obtain the above lemma by the triangle inequality of the norm.However,it is not easy to extend this result from the category of Banach algebras to the category of rings because of the different definition of quasinilpotent elements (see Lemma 1.1).In[14],the authors deduced Lemma 2.1 in the framework of rings by totally different techniques.We are now in a position to establish the extension of Cline’s formula for generalized strong Drazin inverse.

Theorem 2.2Let a,b,c,d∈A satisfy bac=bdb and cdb=cac.Then

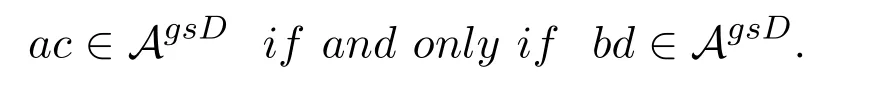
In this case,

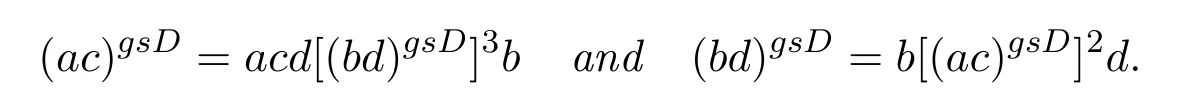
ProofSuppose thatbd∈AgsDandx=(bd)gsD.Thenbd∈AgDandxis also the generalized Drazin inverse ofbd.Sety=acdx3b.By Corollary 2.1,we have (ac)gD=acdx3b.This implies thatysatisfies

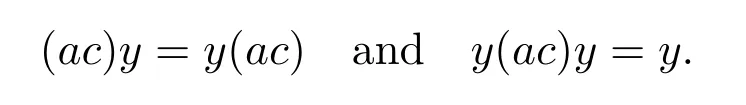
In order to provey∈AgsD,we only need to proveac−(ac)y∈Aqnil.Definec′=c(1−dx2b) andd′=d(1−x).Then

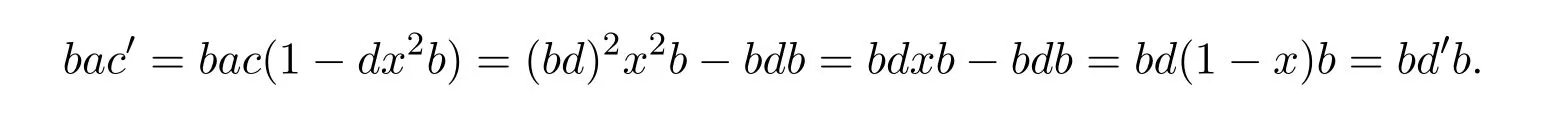
Also,

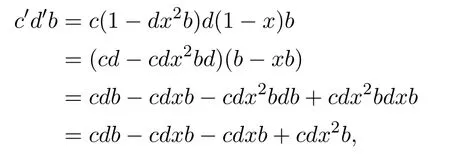
and

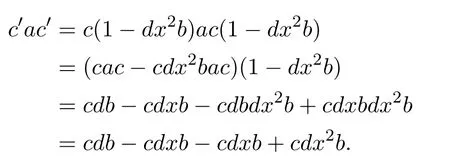
Thusbac′=bd′bandc′d′b=c′ac′.Hencebd′∈Aqnilimpliesac′∈Aqnilby Lemma

2.1.That is,bd−bdx∈Aqnilimpliesac−acdx2b∈Aqnil.From

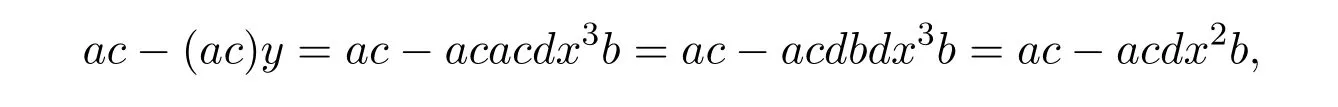
it follows thatac−(ac)y∈Aqnil.