基于Louvain重叠社区发现算法

2020-07-02郭理王嘉岐张恒旭曾窕俊

石河子大学学报（自然科学版） 2020年3期

郭理，王嘉岐，张恒旭，曾窕俊

(石河子大学信息科学与技术学院,新疆石河子 832003)

社会网络根据其使用类型可分为社交网络和社交媒体网络[1]。群组结构是社交网络中观察和理解网络拓扑的一个重要结构，将它抽象到图中，即存在子图内个体关系紧密、子图间个体关系稀疏。Newman[2]把符合这一特点的子图结构称为社区结构。因此，这些在线网络社交关系就形成了复杂的社区结构。社会网络内的社区结构在现实世界中相互重叠[3]，即网络的一个点可以同时存在于多个社区，该结构称为重叠社区，该节点称为重叠节点。

重叠社区发现技术对于分析与研究网络社区间关系具有重要意义。常用重叠社区发现算法有基于局部扩张的LFM算法[4-5]、基于标签传播的COPRA算法[6]和基于派系过滤的CPM算法[7]。LFM算法结果与其适应度增益函数中参数α的选择有关，由于本文研究的动态社会网络重叠社区处在不断的变化中，因此，参数α值无法确定；COPRA算法是一种基于LPA算法重叠社区发现算法，因此其具有LPA算法随机性强、鲁棒性差的缺点；CPM算法发现的重叠社区与人工划分的重叠社区比较相似，但是CPM算法要在运行之前确定社区数量k值，但本文研究社会网络是动态的，其k值不是一成不变的。

目前，常用的非重叠社区发现算法有基于图分割的Kernighan-Lin 算法[8]、基于分裂法的GN 算法[9-10]与Newman算法[2,11]、基于标签传播的LPA算法[12]和Louvain算法[13]等。Kernighan-Lin算法需要指定子图的个数，但本文研究中无法实现预知子图的个数或者子图的大小，所以Kernighan-Lin 算法在本文研究中是不可行的；GN算法时间复杂度高，但本文研究的数据量庞大，所以很难在一个可以接受的时间内获取结果；Newman算法通过计算模块度，将其增长最大的二个社区合并，然而该算法存在的最大缺点是二个节点一旦合并，就没法再分开，这导致可能无法得到理想的结果；LPA算法每次迭代结果不稳定，准确率不高；Louvain算法使用两层迭代的方式，即由自下而上的凝聚法作为外层迭代和由添加交换策略的凝聚法作为内层迭代，可避免单纯凝聚方法合并节点后无法再分开的缺点，具有算法简单直观、容易实现、速度快和效果好的特点。

从效率和效果维度来看，Louvain算法是目前发现非重叠社区方法中最好的，并作为一种简单、灵活、有效的社区发现算法被广泛用于社会网络领域，但是不能发现社会网络中的重叠社区。在实际的社会网络中，重叠社区更加符合人们的行为方式，无法发现重叠社区的Louvain算法可能会丢失最优解，因此，本文在分析研究重叠社区发现算法和非重叠社区发现算法的基础上，提出一种基于Louvain重叠社区发现算法，该算法既能保留原Louvain算法的优点，又能有效发现动态社会网络中的重叠社区，这对于分析与研究网络社区间关系具有重要意义。

1 基于Louvain重叠社区发现算法

1.1 Louvain算法

Louvain算法是Newman等提出的基于模块度最优化的启发式算法，这个算法的思想最早由BLONDEL V D、GUILLAUME JL、LAMBIOTTE R、LEFEBVRE E等在2008年提出，又被称为BGLL算法。

1.1.1 社会网络的表示方法

社会网络通常抽象成图来表示，每个人为图中的一个节点，人与人之间的联系为图中的边。图通常表示为G=(V,E)，其中V表示点集合，E表示边集合，通常用n表示图的节点数，m表示边数。在图中，与一个点相关联的边的数量称为该点的度。对于无向图，图中所有点的度之和是边数的2倍。在使用计算机对图进行处理时，通常使用邻接矩阵A来表示图，邻接矩阵A的(v,w)位置元素使用Avw表示，Avw值为1则表示节点v与节点w之间有边，为0则表示无边。

1.1.2 模块度的定义

模块度Q由Newman等[2]提出，目前常被用于评价无向网络中社区划分结果的好坏程度，一般模块度越大表示社区划分结果越好，其对应的计算公式如下：

(1)

其中,cv和cw分别表示节点v和节点w所在的2个社区，Avw为邻接矩阵A中(v,w)位置的值;其中函数δ(cv,cw)的取值定义为：如果v和w在一个社区，即cv=cw，则为 1，否则为 0;m为网络中边的总数kv表示点v的度,即

(2)

1.2 基于Louvain重叠社区发现算法

1.2.1 算法设计

为了解决Louvain算法无法发现重叠社区的问题，本文对Louvain算法进行改进，提出了基于Louvain重叠社区发现算法，其中，定义模块度Q，并根据增益度函数dq判断一个节点是否具有重叠性，即节点是否为重叠节点。

1.2.2 模块度Q的增益度函数dq

对式(1)进行拆分，得到以下公式：

(3)

假设存在若干个社区，则式(3)中∑v,wAvwδ(cv,cw)为每个社区内边的数量的累加，∑vkvδ(cv,cw)为每个社区内点的度数之和的累加，将对无向图中节点的遍历转换为对社区的遍历，则可以得到化简后的模块度函数

(4)

其中∑in表示社区C内包含边的数量，∑tot表示社区C内点的度数之和。

根据Louvain算法的流程，节点v分配到其相邻节点w所在社区C时，只与节点v、社区C有关，而与其他社区无关，因此，Q的变化量ΔQ可以被表示为：

(5)

其中nv.C是节点v和社区C之间所有连边的数量。

对式(5)进行化简得

(6)

为了简化计算，对式(6)进行适当放缩，将模块度Q的增益度函数dq定义如下：

(7)

其中，nv,C是节点v和社区C之间的所有连边的数量，w是与v相连的在社区C内的点，kv表示点v的度，m为网络中边的总数目。

如果节点加入某个社区的增益度dq与一次迭代后产生的最大增益度maxdq差值小于一定阈值时，则可认为该节点具有重叠性，为重叠节点。在本文的实验中，为了更好地适应社区边数变化的情况，经过多次测试后发现将该阈值设置为1/(2 m)有较好的适应性，但该值也可以根据实际情况进行微调。

1.2.3 算法实现

(1) 根据社会网络关系生成邻接矩阵A(v,w)。本文将社会网络关系抽象成社会网络图G，每个人是社会网络图G中的一个节点，人与人之间的联系为社会网络图G中的边。对社会网络图G进行遍历，生成邻接矩阵A(v,w)，流程如下：

算法：生成邻接矩阵A(v,w)；

输入：社会网络图G；

输出：邻接矩阵A(v,w)。

具体步骤如下:

1.遍历社会网络图G中的每个节点v:

2.遍历与节点v存在边的节点w:

3.将Avw的值设为1

4.返回A(v,w)

(2)进行重叠社区发现。初始时将每个节点即每个用户看作一个社区。依次遍历每个节点，将maxΔQ和maxdq的初始值分别设为-∞和0。对每个节点尝试将其移至其每个相邻节点所在的社区，并计算移动前和移动后的模块度Q的变化ΔQ。ΔQ的变化分为以下三种情况：

情况一：若ΔQ>0，则加入该社区后模块度增大，计算v加入该社区的增益度dq，如果ΔQ>maxΔQ，使maxΔQ=ΔQ，maxdq=dq。

情况二：若ΔQ=0，则加入该社区后模块度不变，不考虑这种情况。

情况三：若ΔQ<0，则加入该社区后模块度减小，不考虑这种情况。

将顶点v移至maxΔQ所在社区和与增益度dq与maxdq相差1/(2 m)以内的社区；重复该过程，直到任何顶点的移动都不能使模块度Q增大。

将遍历后获得的社区看作一个新的顶点，重新生成邻接矩阵，重复本节(2)直到模块度Q不再变化。

(3)基于Louvain重叠社区发现算法实现。

输入为邻接矩阵A(v,w)，输出为社区集合c，具体步骤如下:

1.遍历邻接矩阵A中的每个节点v:

2.将v加入到节点集合vec中

3.将v看作只有一个节点的社区cv，加入到社区集合c中

4.计算社区模块度Q0

5.令m为邻接矩阵A中的边数

6.遍历节点集合vec中的每个节点v:

7.令maxΔQ=-∞,maxdq=0

8.计算社区模块度Q1

9.遍历节点v的相邻节点w:

10.计算将节点v加入到节点w所在社区cw后的模块度Q2

11.令ΔQ=Q2-Q1

12.如果ΔQ>0

13.计算增益度dq

14.如果ΔQ>maxΔQ：

15.maxΔQ=ΔQ

16.cwmax=cw

17.如果dq>maxdq:

18.maxdq=dq

19.cMap[cw]=dq

20.如果maxΔQ>0:

21.将节点v加入到社区cwmax中

22.遍历cMap并将key赋值为cv，value赋值为dq:

23.如果maxdq-dq<1/(2m)且cv≠cwmax:

24.将节点v加入到cv中

25.更新社区集合c

26.否则节点v保持不动

27.计算社区模块度Q2

28.如果Q0≠Q2:

29.清空点集合vec和邻接矩阵A

30.遍历社区集合c中的每个社区cv:

31.将社区cv压缩为一个节点v，将社区cv内节点的边转化为新节点v的环

32.将节点v加入点集合vec

33.遍历社区cv的不在点集合vec中的相邻社区cw:

34.将社区cw压缩为一个节点w，将社区cw内节点的边转化为新节点w的环

35.将社区cv与社区cw之间的边转化为节点v与节点w之间的边

36.将节点w加入点集合vec并更新邻接矩阵A

37.跳转1

38.返回社区集合c

2 实验测试

2.1 基于Louvain重叠社区发现算法与Louvain算法的对比

经典数据集Zachary’s Karate Club Network[14]包含34个结点与78条边，本文采用该数据集对本文提出的基于Louvain重叠社区发现算法与Louvain算法进行实验测试对比，用于检测本文算法是否可以发现重叠节点。

先使用Louvain算法对 Zachary’s Karate Club Network数据集进行社区发现，对数据结果进行可视化处理，运行结果如图1a所示，其中一个圈表示一个社区，一个圈内的节点即为同一个社区内的节点。从图1a可以看出，原始的Louvain算法在Zachary’s Karate Club Network数据集中发现4个非重叠社区。

再使用本文提出的基于Louvain重叠社区发现算法对Zachary’s Karate Club Network数据集进行重叠社区发现，结果如图1b所示。从图1b可知:基于Louvain重叠社区发现算法不仅发现了Louvain算法发现的4个非重叠社区，并且还发现了1个重叠社区(3,10,29,32,34)。

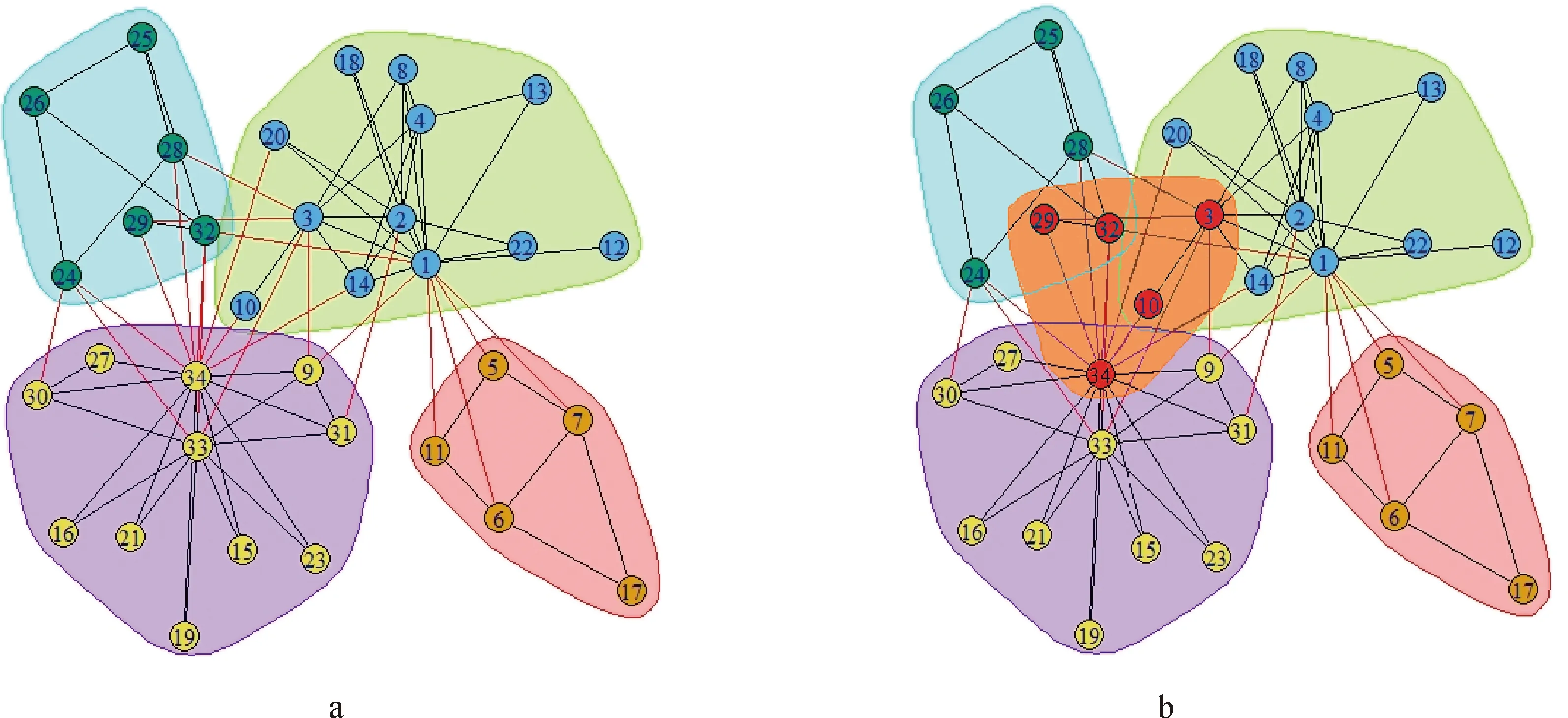
图1 Louvain算法(a)、基于Louvain重叠社区发现算法(b)的结果

为了方便描述，Louvain算法发现的社区名称定义见表1。

表1 社区名称定义

根据表1中社区名称的定义，重叠社区与1号社区存在重叠节点(29,32)，与2号社区存在重叠节点(3,10)，与3号社区存在重叠节点(34)。在Zachary’s Karate Club Network数据集中认为节点2、3、34、29、14是重叠节点[14]，由此可知本文提出的基于Louvain重叠社区发现算法发现了大部分的重叠节点，从而验证了基于Louvain重叠社区发现算法可以有效发现社会网络中的重叠社区。

2.2 与其他重叠社区发现算法对比分析

式(1)是常用于评价非重叠社区划分结果的指标。SHEN H等[15]对模块度Q函数进行改进，提出了重叠社区模块度EQ函数，用于评价重叠社区的划分结果，计算出的EQ值越大说明重叠社区的划分结果越好。EQ计算公式为

(8)

式(8)中，C代表社区集合，V表示顶点集合，Ov代表节点v所属的社区的个数，kv表示点v的度，m为网络中边的总数目。

本文使用经典数据集American College Football[9]对基于Louvain重叠社区发现算法与CPM算法、LFM算法和COPRA算法进行实验测试对比，并使用重叠模块度EQ和运算时间对结果进行综合评价。

American College Football数据集是根据美国本科生足球联赛创建的一个复杂的社会网络，该网络包括115个节点和616条边。为了避免随机性，本文对每个算法重复运行100次后取平均值，结果如表2所示。

表2 American College Football数据集实验结果

从表2可知：本文提出的基于Louvain重叠社区发现算法运算时间比LFM算法降低了23.06%，且重叠模块度EQ较LFM算法提高了12.81%，表明基于Louvain重叠社区发现算法明显优于LFM算法，而且比CPM、COPRA算法运算时间分别提高12.62%和7.15%，重叠模块度EQ分别提高17.05%和9.45%。

虽然基于Louvain重叠社区发现算法运算时间比CPM、COPRA这二种算法差，但是其重叠社区的划分效果优于CPM、COPRA这二种算法，因此，综合运算时间与重叠模块度EQ，基于Louvain重叠社区发现算法要优于其他算法。

2.3 基于转发关系的微博重叠社区发现测试

转发关系属于交互关系的一种。由于新浪微博的推荐策略，在参与事件讨论中，微博用户之间的关注关系可能并不突出，因此，交互关系微博社区更能体现真实的微博网络社区结构[16]。

本文设计基于转发关系的微博重叠社区发现测试实验，用于验证该算法在实际应用中的效果。本文采用北京理工大学张华平博士提供的微博语料数据[17]，该语料中包括约500万条微博内容语料。根据2013年4月19日和20日的微博语料识别出其中的一个热点话题为“雅安地震”，该话题包含微博数量5 685条，其中存在关注关系的用户有83个，而存在转发关系的用户有247个，也证实了在同一个话题特别是非常规突发事件中，用户之间的关注关系可能不会特别突出。因此，本文使用转发关系构建社会网络，即一个用户为一个节点，如果用户A与用户B之间存在转发关系，则A与B之间有边。

根据本文提出的基于Louvain重叠社区发现算法进行重叠社区发现，并将最终结果可视化,得到的结果如图2所示，其中一个圈表示一个社区，一个圈内的节点即为同一个社区内的节点。

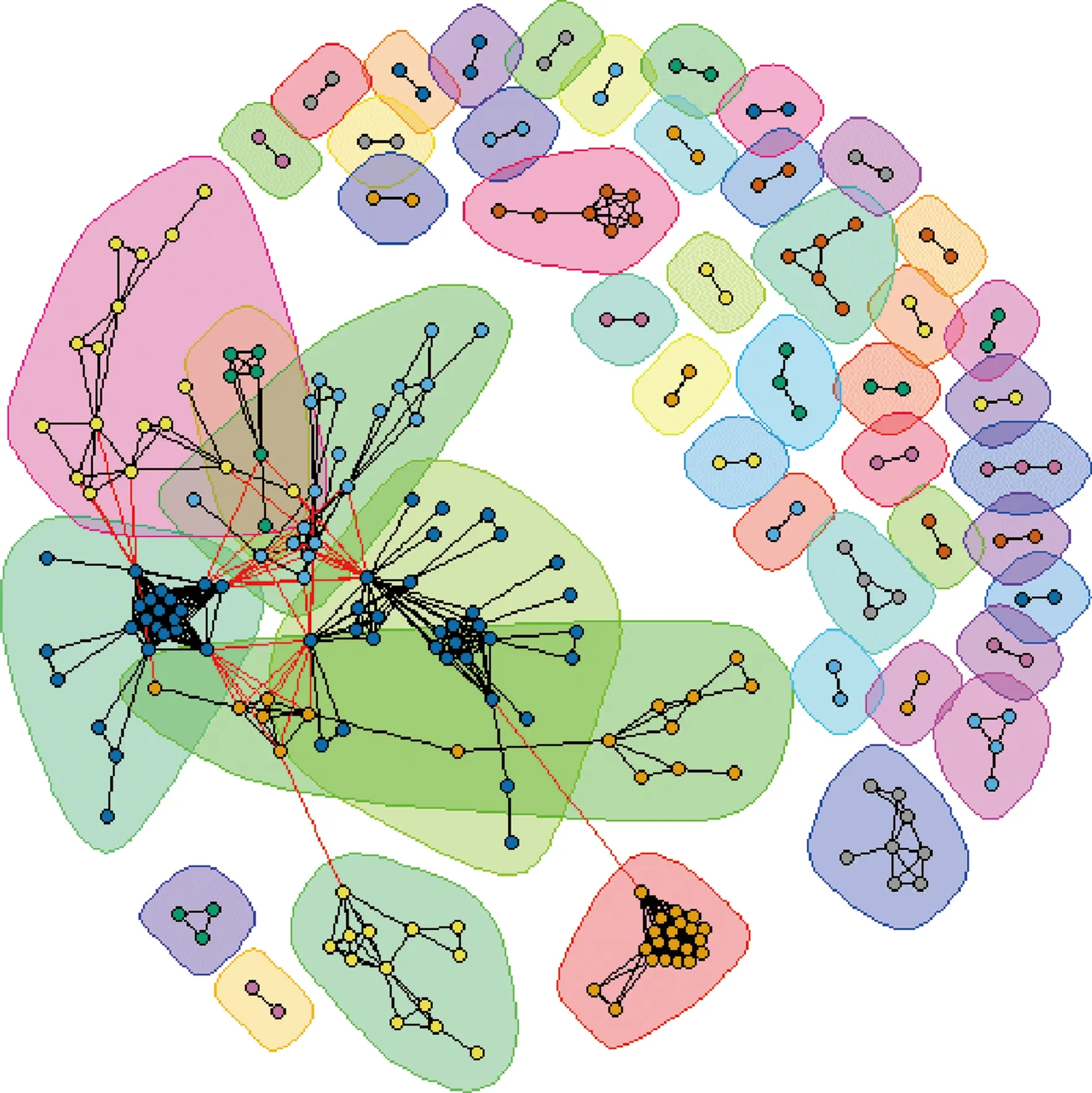
图2 运算结果

由图2可以看出，本文基于Louvain重叠社区发现算法在测试数据上总共发现64个动态社会网络社区，其中存在有6个重叠的动态社会网络社区。与“雅安地震”热点话题手动划分的社区结果对比之后发现，本文提出的算法实验结果与手动划分的情况基本相符，说明本文提出的基于Louvain重叠社区发现算法可以有效发现重叠的动态社会网络社区。