建筑管道的流固耦合动力学分析
2020-07-01徐涛王波周东肖孜李峰余凡
徐涛 王波 周东 肖孜 李峰 余凡

摘 要:针对民用建筑管道振动问题,采用流固耦合对管道进行流场及模态分析,通过流场分析得出由于脉动压力的影响,其湍动能也有较大波动,且在弯管处的湍动能波动最为明显,且弯管处伴随着二次流现象,极大的增加了管道内的能量损失,也是引起管道振动的一部分原因;通过模态分析得出在第一阶固有频率与压力脉动频率较为接近,有较高共振的可能;为消除共振,对管道施加不同约束,得出固定约束应与弯管保持一定的距离,同时在弯管两端同时施加约束能够使管道振动幅度最小;通过实验与仿真对比,说明了流固耦合在管道振动分析中具有一定的可行性,且具有一定的工程应用价值。
关键词:建筑管道 流固耦合 管道振动 压力脉动
中图分类号:V216.8;TH137 文献标识码:A 文章编号:1674-098X(2020)05(a)-0085-05
Abstract:Flow field and modal analysis of pipelines using fluid-solid coupling for civil building pipeline vibration problems,The turbulent energy is affected by the inlet pressure pulsation and has large fluctuations in the pipeline, and is most obvious at the elbow. At the same time, accompanied by the secondary flow phenomenon, the energy loss in the pipeline is greatly increased and the pipeline vibration is caused; Through modal analysis, it is found that the first-order natural frequency is close to the pressure pulsation frequency, and it is highly probable that resonance occurs;In order to eliminate the resonance phenomenon, different constraints are applied to the pipeline to analyze, and it is concluded that the fixed constraint should be kept at a certain distance from the elbow, and the simultaneous application of the constraint at both ends of the elbow can minimize the vibration amplitude of the pipeline;The comparison between experiment and simulation shows that the fluid-solid coupling has certain feasibility in pipeline vibration analysis and has certain engineering application value.
Key Words: Building pipe; Fluid-structure coupling; Pipe vibration; Pressure pulsation
管道系統作为一种重要的工程结构,在给水排水、消防、供暖等生活设施中有着广泛的应用,随着人们对生产、生活环境要求的提高,其振动噪声问题越来越突出。
管道的强烈振动会使管道与附件、管道之间的连接处发生磨损松动,引起管道和支架材料的疲劳损伤,甚至发生断裂,产生严重后果。同时管道还起到了传递振动、噪声的作用,不利于对振动噪声的控制和隔离,在民用建筑中如减震措施不到位,则地下室内水泵的振动噪声沿管道四处传播,高层的排水流过低层时产生较大的压力脉动,也会使低楼层的管道产生振动噪声。同时还可能使管道连接处发生断裂,使得房屋墙壁进水破坏住户装修及电器。当水流渗入电力设备还会产生较大的安全隐患。
引起管道振动的原因有很多,主要包括流体脉动、流体冲击、共振等几个方面[1-6],常用的减振方法也有很多,如改变管路布局、在管道的适当位置安装消振器、在管路上安装缓冲器[7-8],但这些方法在民用建筑中不太适用,目前很多的民用建筑管道均采用的固定支撑来进行减振,但是固定支架会对管道产生较大的应力[9],所以管道的固定位置以及应力大小的确定久显得尤为重要。
本文通过对民用建筑常用的弯管进行分析,通过流固耦合对其仿真来确定管路的振动频率以及对其优化,同时通过实验验证证明了流固耦合对弯管的分析具有一定的可行性。
1 建模与边界条件
1.1 计算模型
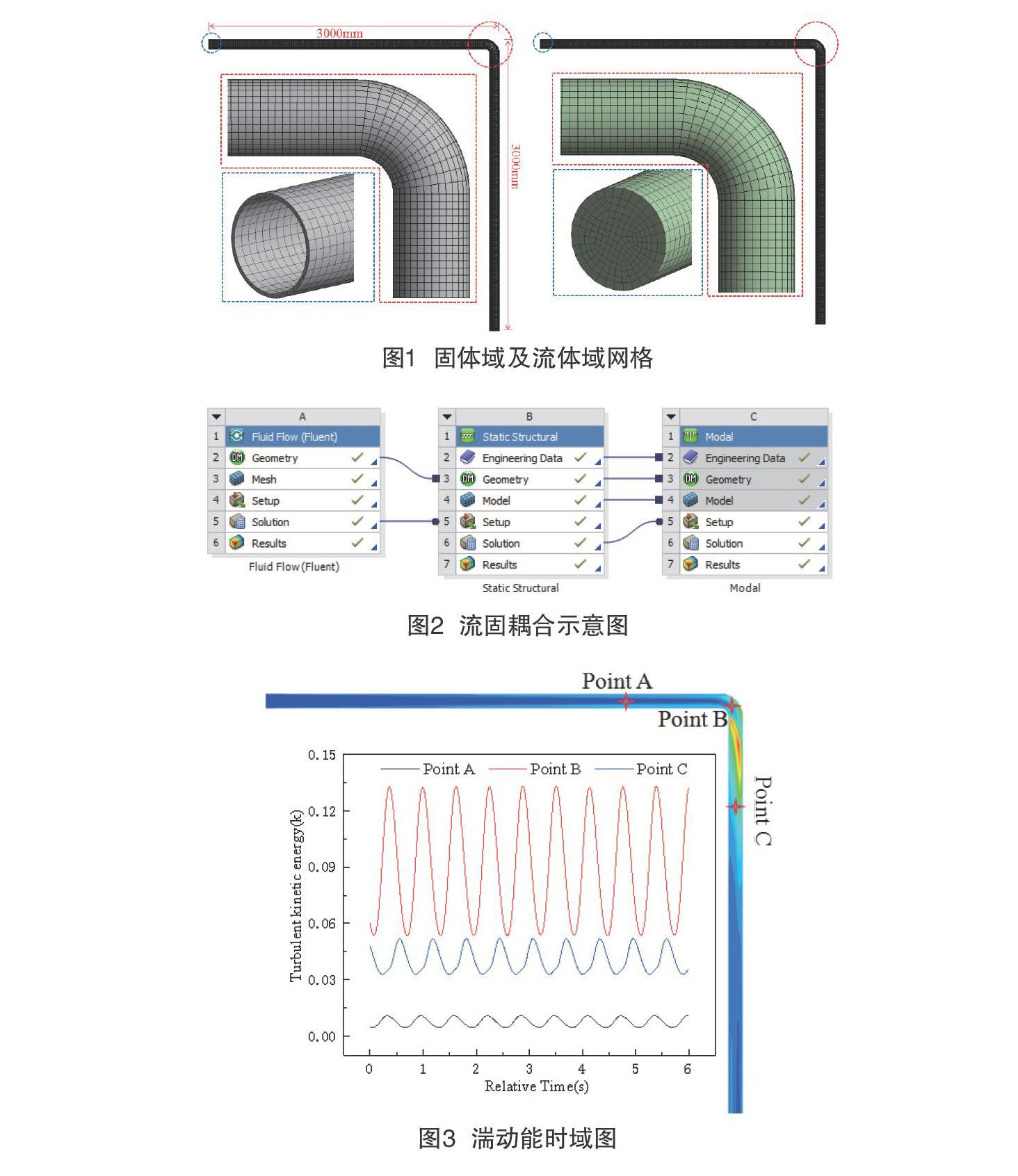
选择常用的一条管路系统,采用SolidWorks建模、Meshing进行网格划分。其几何流体域和固体域网格如图1所示,本文采用流固耦合方式对管道振动进行分析,钢管内的流体流动采用fluent进行仿真,钢管的结构仿真采用Static Structural 进行仿真,两者的数据通过流固耦合面(FSI,Fluid-Structure Interaction)进行数据传递,其模态分析是以Static Structural仿真的结果为初始条件采用Modal 模块进行仿真,如图2所示。
钢管外径100mm,厚度4mm。其流体与固体参数见表1。
1.2 边界条件
采用Fluent-Workbench流固耦合分析,其边界条件也分为流体边界条件和固体边界条件。
由于流体域内的流动存在着压力脉动,所以其入口速度及压力并非始终保持不变,故该仿真采用压力入口,且通过UDF(User Define Function)对管道入口施加一个连续脉动压力,使其压力随着时间按余弦变化来定义入口压力,其UDF如下:
将Fluent仿真得到的壁面压力结果通过FSI设置为Static Structural中仿真的初始条件进行静力学分析,最后将静力学分析结果设置为Modal的初始条件进行模态分析,得到其6阶模态及其频率。
2 计算结果
2.1 流体域结果分析
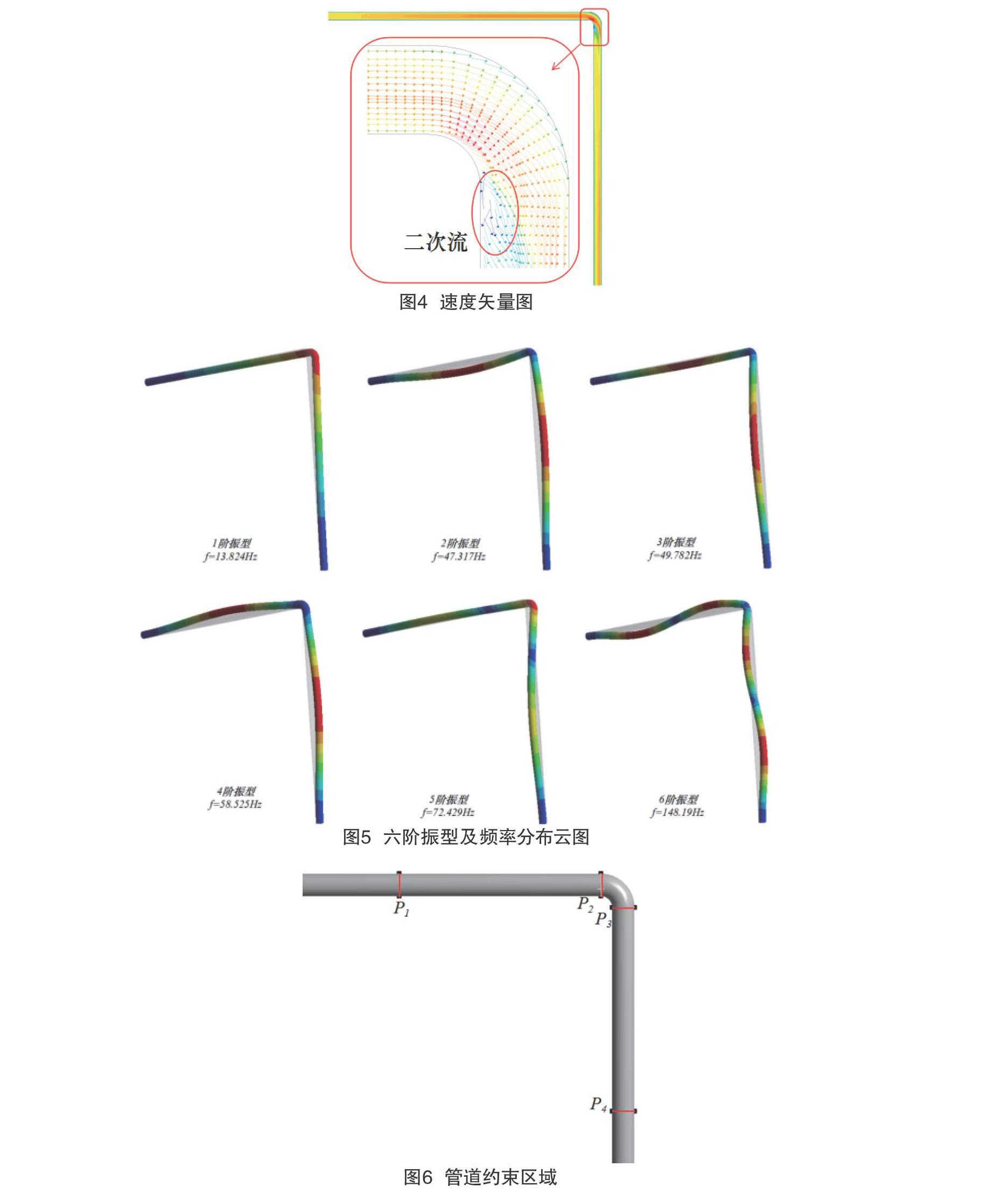
湍流动能是湍流速度的涨落有着密切关系,湍动能越大,能量损耗越多,速度波动越大。图3为对管道内三点湍动能实时监测图,图4为速度矢量图。从图3中可以看出当管道内水流流经A、B、C三点时,其湍动能均有明显变化,由于入口脉动压力的影响,其湍动能也会产生一定的脉动。在A点出湍动能明显小于B、C两点,这是由于入口流经A点的该段管道为直管,对速度无明显影响,其湍动能的波动为入口压力脉动的影响所造成的,但在经过弯管B处时波动幅度最大,这是由于水流在经过弯管时由于离心力的作用,管道内的流体均会向管道外侧挤压,从而是弯管内侧的流体无法完全接收到前面传递的能量,从而产生较大的速度差,使其湍动能有着明显的变化,根据伯努利方程可以知道速度与压力成反比,当弯管有着较大的速度差时,就会产生较大的压力梯度,当产生逆压梯度时,管道内就会产生如图4的二次流现象。二次流现象对管道振动有着较大影响,同时也伴随着较大的能量损耗,所以在进行管道设计时要尽量避免二次流。随着水流的流动,当水流到达C点时,其弯管对该点的影响明显减弱,其湍动能波动也随着减弱。
2.2 固体域结果分析
模态分析是研究结构动力学特性的一种方法,其最终目的是识别出系统的模态阐述,为结构的振动特性分析、振动故障诊断和预报以及结构动力学特性的优化设计提供依据。模态振型仅有助于理解结构振动,并不代表真实位移,模态分析中变形结果是相对变形分布趋势,不代表真实数据,通过Static Structural能得到振型和位移结果,但不能得到分布趋势。
图5为六阶振型分布云图,第2、3、4、6阶振型最大位移均位于两段直管中部,去哦自己跑美国第2、3阶振型频率接近,且均为拉伸振动,4、6阶振型为弯曲振动;第1、5阶振型最大位移位于弯管处,第1阶为拉伸振动,第5阶为弯曲振动;从图中还可以看出第一阶振型的固有频率为13.824Hz与脉动压力给的10Hz频率非常接近,很有可能产生共振现象,所以很有必要对该管道进行一定约束,改变其频率使其减小振动的同时避免共振产生。
3 约束位置对管道振动的影响
由于模态分析发现未经约束的管道容易产生共振现象,故需对管道进行约束分析。其约束点见图6,工况见表2。
通过对不同工况进行模态分析及静力学分析,得出不同工况下的六阶振型频率(见表3)和不同工况下的最大位移几最大应力(见图7)。
当给管道施加一个约束时,其固有频率都有不同程度的升高,但在给管道施加約束时不仅要考虑其共振与振动频率,同时还需要考虑支架约束时所产生的最大应力,当应力过大时,会对固定在墙体的支架产生损坏,同样也会产生安全隐患,所以在对管道进行约束时需要综合考虑。结合表3和图7可以看出,当约束在直管处时,其最大应力及最大位移均要远远小于约束处于弯管处的工况,所以在进行支架固定时尽量避免在弯管处,当约束点位于P4时,相对于P1,其最大应力有所上升,但最大位移减小,且两者频率较为接近。所以在进行支架固定时可以在弯管两端进行固定,从工况6中可以看出,当同时固定P1和P4时,其最大应力在工况1与工况5之间,但最大位移为所有工况中最小。
故在进行管道支架固定时,当只能设置一个支架应当与弯管保持一定的距离,若对支架数量无较大限制,可以在弯管前后两段进行约束,这样管道振动最小,同时也最不容易与水流产生共振。安全系数最高。
4 实验验证
为验证管道约束对管道振动有影响,现采用Lab VIEW软件与cRIO 9035嵌入式实时采集与控制器对管道表面进行信号采集。将加速度传感器贴于管道上,进行实时监测,如图8所示。
通过对水流通过时的管道进行加速度监测,得到其稳定时加速度分布曲线如图9所示。
从图中可以明显看出无约束时加速度明显大于有约束的管道,加速度大小也体现了管道的振动幅度,这与前面仿真结果较为吻合,说明采用流固耦合对管道进行仿真具有一定的可行性。
5 结论
通过对常用弯管的有限元建模进行流固耦合分析,可以得出:
(1)通过其无约束管道流场分析可以看出当水流经过弯管处时湍动能波动较大,同时弯管内侧还伴随着二次流的产生,极大地增大了能量损耗及管道振动。
(2)通过对无约束管道进行模态分析可以看出管道的第一阶振型频率与入口的压力脉动频率较为接近,容易产生共振现象,需要对管道进行一定的约束来消除共振现象。
(3)根据不同位置的约束对管道模态进行分析,得出在进行施工时,对管道进行约束尽量避免在弯管处直接约束,应尽量与弯管保持一定的距离,最好能在弯管两侧进行共同约束。
(4)通过数值仿真对管道进行减振分析,同时用实验进行了验证,不仅节约了改造成本,而且能够有效的控制管道振动延长管道使用寿命,在工程实际中有一定的指导作用。
参考文献
[1] 任建亭, 任建亭, 姜节胜.输流管道系统振动研究进展[J]. 力学进展, 2003, 33(3):313-323.
[2] 马飞, 曲世琳, 吴一民. 给水管网非恒定流动数值计算方法[J]. 工程科学学报, 2009, 31(4):423-427.
[3] 郝婷玥 陈贵清, 徐光耀. 输流管道振动问题的研究[J]. 水利科技与经济, 2008, 14(7):32-35
[4] 张智勇, 沈荣瀛. 充液直管管系中的固—液耦合振动响应分析[J]. 振动工程学报, 2000, 13(3):455-461.
[5] Chen J K L, Noguchi H, Koshizuka S. Fluid–shell structure interaction analysis by coupled particle and finite element method[J]. Computers & Structures, 2007, 85(11):688-697.
[6] Klaus-Jürgen Bathe, Zhang H . A mesh adaptivity procedure for CFD and fluid-structure interactions[J]. Computers & Structures, 2009, 87(11-12):604-617.
[7] 赵力电. 压力管道振动分析[J]. 管道技术与设备, 2006,15(6):31-32.
[8] 郄殿华. 压力管道振动的解决实例[J]. 石油和化工设备, 2009, 12(6):25-26.
[9] 赵子琴, 李树勋, 徐登伟. 管道振动的减振方案及工程应用[J]. 管道技术与设备, 2011,10(3):54-56.
