基于NSST的PCNN-SR卫星遥感图像融合方法*

曹义亲 杨世超 谢舒慧

华东交通大学软件学院, 南昌330013

0 引言

卫星传感器可以检测和记录地表反射的电磁波，而遥感图像是存储这类信息的载体，用于环境[1]和气候监测[2]、以及土地覆被变化检测[3]和分类[4]等应用。许多地球观测卫星，如Landsat、IKONOS、高分一号、QuickBird等，可以在相同的覆盖范围内同时拍摄全色图像和多光谱图像。由于反射率值随地表覆盖和光谱波段的不同而变化，多光谱[5](multispectral, MS)图像比全色(panchromatic, PAN)图像能够记录更多的地表信息[6]。然而，考虑到传感器的信噪比和权衡，MS图像的空间分辨率通常低于PAN图像。因此，图像融合的目的是通过融合共配准的PAN图像和MS图像，最大限度地利用空间和光谱信息。理想情况下，融合图像应具有PAN图像的空间分辨率，并保留MS图像的光谱信息。

近年来，大量的基于遥感图像的图像融合[7]方法被提出，一般来说，大致可以分为2类方法：空间域和变换域。空间域方法是直接对图像像素点进行操作，而变换域方法需要先对图像进行频域变换，再对变换后的系数进行融合。在变换域方法中，比较常用的有：非下采样轮廓波变换、Curvelet变换和非下采样剪切波变换。文献[8]提出了基于非下采样轮廓波变换的耦合区域信息特征提取的卫星遥感图像融合算法，通过构建区域特性的融合规则，从而对高低频子带系数进行处理。文献[9]提出了基于二代Curvelet变换与近似度制约规则的卫星遥感图像融合算法，采用结构相似度模型对高频系数进行处理。文献[10]提出了一种基于非下采样剪切波变换的耦合边缘制约的卫星遥感图像融合算法，将边缘制约模型用于处理高频系数，在一定程度上提高了融合图像的清晰度。

为了对卫星遥感图像融合效果进行改善，并在一定程度上提高卫星遥感图像融合算法的效率，本文提出了一种全新的思路，将源图像进行NSST变换，对得到的高频分量采用改进的PCNN方法进行处理，用改进的拉普拉斯能量和当作其外部激励，分别选取梯度能量、标准差作为其连接强度，将2种不同结果进行加权处理，得到最终的点火映射图；采用改进的稀疏表示对低频分量进行融合，最后进行NSST逆变换，得到一个细节信息比较丰富的融合图像，同时，算法效率得到较大提升。

1 NSST的基本理论

在传统仿射系统的基础上，Easley等将几何与多尺度相结合，提出了一种新型的多分辨率分析工具-非下采样剪切波(NonSubsampled Shearlet Transform, NSST)，它不仅吸收了小波理论的最新研究成果，而且具有严格的数学基础。在二维情况下，该仿射系统表达式如式(1)所示:

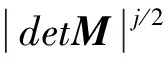
j,l∈Z,k∈Z2}

(1)

其中，ψ∈L2(R2)，|detN|=1；j为分解尺度，l为方向参数，K为剪切参数；M为各向异性矩阵，N为剪切矩阵，Z为整数域。

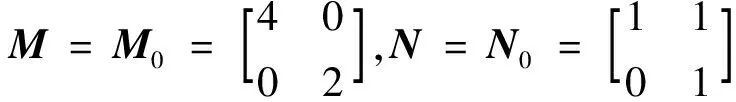
NSST变换主要包括多尺度分解和多方向分解。通过对源图像进行多尺度分解，可以得到高频分量和低频分量。多尺度分解主要通过非下采样金字塔(Non Subsampled Pyramid，NSP)实现，而多方向分解则由改进的剪切滤波器(Shearlet Filter，SF)实现，具体流程如图1所示:

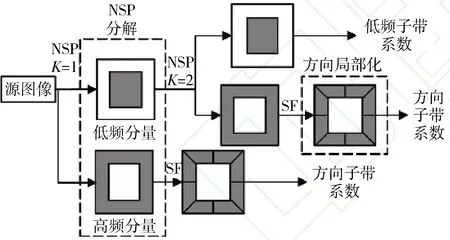
图1 NSST的多尺度多方向分解过程

2 稀疏表示理论

稀疏表示(Sparse Representation,SF)[11]是一种对超完备字典的“少数”原子进行线性组合，用来表示信号的模型。在稀疏表示建模中，输入信号可以表示为:

y=Da

(2)

其中，向量a∈RK表示信号y的系数矩阵，D∈Rn×K(K>n)表示字典矩阵。通过对以下优化问题进行求解，从而得到最稀疏解:

(3)

在稀疏表示模型中，一个比较重要的任务就是需要构建一个适当的字典。一般来说，有2种方法可以获得字典。第1种方法是使用分析模型。第2种方法是从大量的训练图像块中获取字典。字典学习模型[14]可以用式(4)求得：

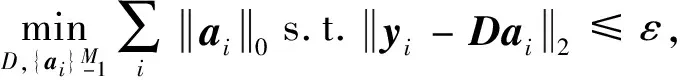
i∈{1，…，M}

(4)

上述最小化问题可以使用K奇异值分解(K Singular Value Decomposition,K-SVD)来解决。

3 脉冲耦合神经网络(PCNN)

脉冲耦合神经网络(Pulse Coupled Neural Network,PCNN)[15]是一种简化的神经网络。该网络模型是根据生物视觉神经系统的工作原理，由Eckhorn提出，通过模拟猫脑视觉皮层同步脉冲爆发现象，从而建立模型。

标准的PCNN模型主要由3部分组成：刺激接收场，脉冲调制场和脉冲生成场。当把PCNN模型与图像相结合时，图像的每个像素与网络中的神经元一一对应，迭代公式如下所示:

F(n)=S

(5)

L(n)=eaLL(n-1)+VL∑WY(n-1)

(6)

U(n)=F(n)(1+βL(n))

(7)

(8)

θ(n)=e-aθ×θ(n-1)+VθY(n-1)

(9)

其中，n是迭代次数,F和L分别代表第1个反馈输入神经元和连接输入,β是连接强度,U是全部内部活动,θ是内部活动动态阈值,Y是PCNN的脉冲输出,W是神经元矩阵之间的连接权重,VF，VL和Vθ是放大因子,aF，aL和aθ为时间常数。

4 PCNN-SR图像融合算法

4.1 基于PCNN的高频子带融合规则

最原始的PCNN模型的连接强度，通常会采用不变的值。而人眼对不同特征区域的响应程度存在差异，导致所有神经元的连接强度不会完全一致。所以，连接强度的取值并不是固定常数。因此，本文分别采用梯度能量、标准差作为其连接强度。

梯度能量：

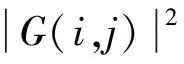
(10)

G(i,j)=

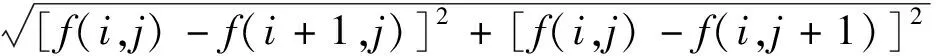
(11)

标准差：

(12)

其中，f(i,j)为位置(i,j)的高频子带系数，像素点的邻域大小M×N，avg为求平均值函数。

为了更好地提高图像融合效果，将外部激励设置成改进的拉普拉斯能量和:

CSL(x,y)=

|2f(x,y)-f(x-1,y)-f(x+1,y)|+

|2f(x,y)-f(x,y-1)-f(x,y+1)|+

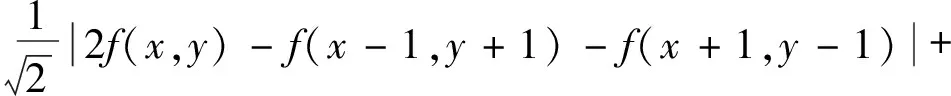
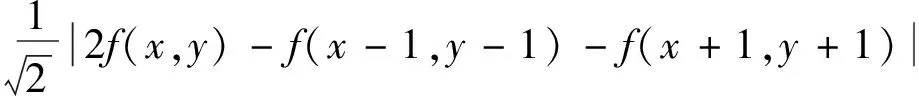
(13)

(14)

(15)

其中，f(x,y)为对应子带系数值，w为区域窗口的权值。将CEOL当做该模型的外部激励。

图像融合规则如下：

1)通过NSST变换对图像进行分解，得到高频子带系数HA和HB，根据PCNN神经网络的运作方式，可以得到不同的输出，分别为OA,E，OB,E，OA,S和OB,S。

2)根据输出值的不同，构造加权函数：

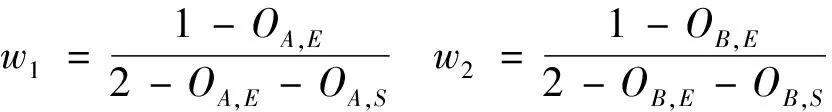
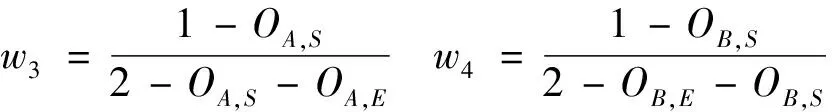
(16)

3)根据不同的权重，构造点火映射图：

OA=w1OA,E+w3OA,SOB=w2OB,E+w4OB,S

(17)

4)根据点火映射图，确定融合规则，如下所示：

(18)

4.2 基于SR的低频子带融合规则

本文对低频子带系数采用改进的稀疏表示进行处理，采用K-SVD方法获取字典，最后采用正交匹配追踪算法(OMP)得到稀疏系数矩阵。具体步骤如下所示：

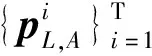
(19)

(20)

其中，D为字典。

3)计算图像块的显著性：

(21)

其中,Lμ代表图像块的均值，Lw代表图像块的高斯滤波，‖‖为欧式距离。

4)根据显著性的大小构造加权映射

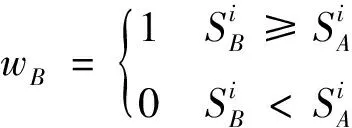
(22)

5)构造融合规则：

(23)

融合向量的计算如下：

(24)

4.3 算法流程

算法主要的步骤如下所示：

1)将源图像分别进行NSST变换，得到高频子带系数和低频子带系数。

2)将高频子带系数采用PCNN模型进行处理。将外部激励设置为改进的拉普拉斯能量和，将梯度能量、标准差作为其连接强度，得到2种不同的点火映射图，对点火映射图进行处理，得到高频融合系数。

4)采用改进的稀疏表示对低频子带进行处理，得到稀疏系数矩阵，根据融合规则进行选择。

5)将获得的字典和稀疏系数矩阵进行重构，得到低频融合系数。

6)对低频融合系数和高频融合系数进行NSST逆变换，得到最终的融合图像。

具体的流程如图2所示。

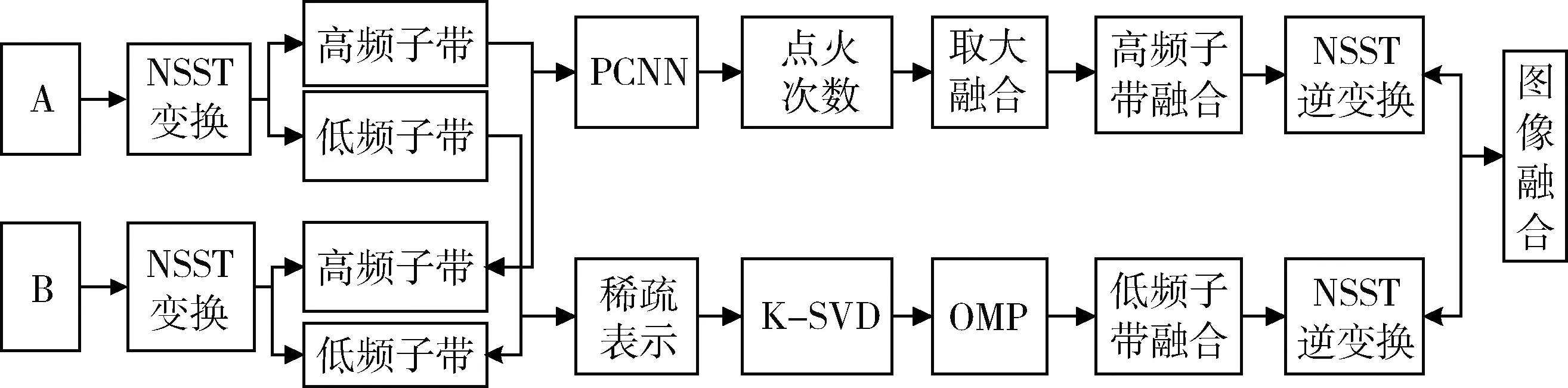
图2 算法流程图

5 实验结果分析

本实验采用win7系统，在主频1.70GHz、内存为8G的笔记本电脑上运行，软件环境是MATALAB R2016b。选择地球眼卫星数据和快鸟卫星数据作为源图像，多光谱图像的大小分别为256×256，全色图像的大小为1024×1024，如图3所示。

图3 实验源图像

为了能更好地说明本文算法的融合效果，将本文算法与3种不同的算法进行对比，分别为：NSCT算法、SML-EN算法[16]、EN-SR算法[17]。对于NSCT算法，高频分量用能量取大方式处理，低频系数采用平均方法处理。对于SML-EN算法，高频分量采取SML作为改进PCNN算法的输入，低频分量用能量取大方式处理。对于EN-SR算法，低频分量用稀疏表示方法处理，高频分量用能量取大方式处理。实验结果如图4和图5所示。

图4 地球眼卫星图像实验结果对比

图5 快鸟卫星图像实验结果对比

从图4中可以看出，图4(a)～(d)的融合效果有明显的差异。从主观方面来评价，(a)图整体比较模糊。(b)图虽然在清晰度方面处理得比较好，但细节部分丢失比较严重。(c)图边缘部分出现了变形，降低了图像的整体效果。(d)图细节信息比较丰富，对比度比较高。

从图5中可以看出，图5(a)和(b)丢失了比较多的信息，在图5(c)中，图像的层次感比较低。图5(d)中图像的空间分辨率和光谱分辨率都比较高。

为了能更好地对本文算法的效果进行验证，采用常用的客观评价指标对图像融合效果进行评估，其中IE代表信息熵、AG为平均梯度、SD为标准差、SF为空间频率、MI为互信息。

表1～2给出了相关融合方法客观指标的比较。

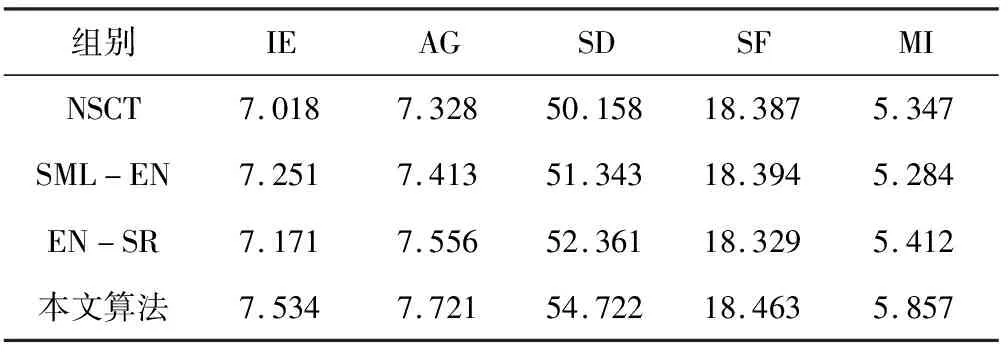
表1 地球眼卫星图像融合结果的客观比较

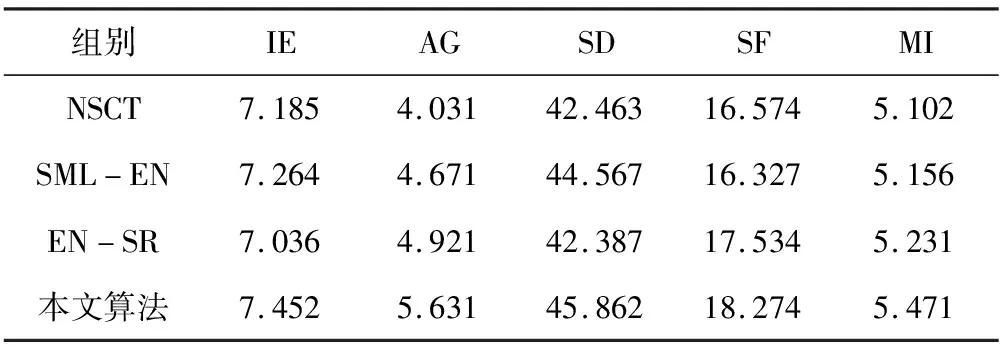
表2 快鸟卫星图像融合结果的客观比较

从表1和表2可以看出，与NSCT算法、SML-EN算法和EN-SR算法相比较，本文方法在客观评价指标IE、AG、SD、SF、MI上，都占有一定的优势。

在时间复杂度上，本文分别对4种算法在2组图像上进行了测试，结果大致相同，如表3所示。从表中可以看出，本文算法具有较大优势。

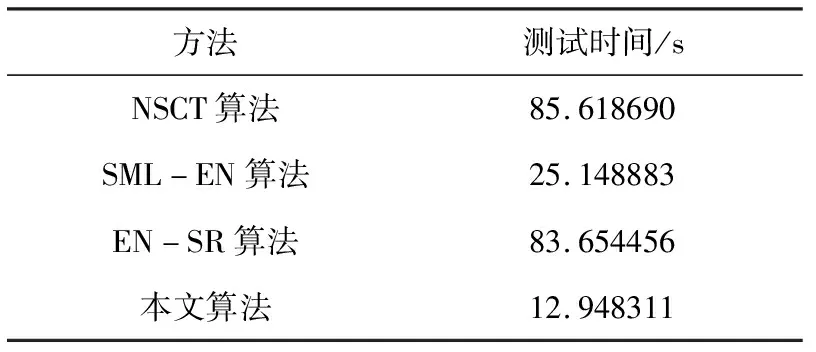
表3 不同图像融合算法的时间比较

6 结论

针对卫星遥感图像，通过对高空间分辨率的全色图像和低空间分辨率的多光谱图像进行融合，从而得到高空间分辨率的多光谱图像。采用基于非下采样剪切波变换的脉冲耦合神经网络与稀疏表示相结合的图像融合方法对全色图像和多光谱图像进行处理。实验结果表明，与其他3种图像融合算法相比较，本文在主观视觉和客观评价上都取得了不错的效果，并且在时间复杂度上有着明显的提升。