弧形钢闸门有限元分析及结构优化

王学亮，杜蔚琼，李东明,3，任泽俭

(1.枣庄市鸿禹水利工程监理中心，山东 枣庄 277000；2. 水利部水工金属结构质量检验测试中心，河南 郑州 450044；3.中国地质大学(北京)，北京 100083；4.南水北调东线山东干线有限责任公司，山东 济南 250109)

1 绪论

弧形钢闸门是水电站发电系统中重要的金属构件之一，由于弧形钢闸门为空间三维结构，其结构特性、边界条件较为复杂，传统的设计与校核仍然按照钢闸门设计规范采用平面受力计算的方法，难以顾及到结构空间作用，因而无法完全反映闸门的真实受力状态。随着计算机技术的发展，有限单元数值模拟法逐渐由2D平面应用过渡到3D空间应用，其计算结果准确且完全适应于各种大型复杂结构，诞生了诸如ANSYS等一系列优秀的商用有限元软件[1- 4]。

ANSYS是融合结构分析等于一体的大型CAE软件包，专门用来解决各种工程问题。经过多年发展，ANSYS由经典界面逐渐发展为ANSYS Workbench整合多种物理场独立分析及场间耦合分析的大型CAE软件系统[5]。本文基于ANSYS Workbench，以某抽水蓄能电站泄水孔弧形钢闸门为研究对象，用SolidWorks建立弧形钢闸门的三维模型，导入ANSYS Workbench中用实体单元划分网格，建立包含边界条件的弧形钢闸门三维有限元模型，在静态挡水和启门瞬间两种工况分别进行求解，在后处理中提取计算结果，观察支铰约束反力与面板设计水压力对应情况，查看并分析主结构承力构件的VonMises应力值、位移值的大小与分布情况，根据NB35055—2015《水电工程钢闸门设计规范》评估弧形钢闸门在两种工况下的结构安全性，对比分析并研究了门叶和支臂在两种工况下综合VonMises应力和位移值的变化特点，分析了面板底缘处局部应力集中的原因，采用结构补强的方法对面板底缘受力结构进行优化并再次分析，其局部应力集中完全消除。

2 有限元模型的建立

2.1 工程背景

某抽水蓄能电站下库导流泄放洞弧形钢闸门，设计水头为64.0m。闸门弧面半径6.0m，吊耳轴至底坎高度3.8m，属于高水头潜孔弧形闸门。其结构主要特点是门体尺寸中等，单组上下支臂，支臂构件截面为工字形，上下支臂间通过多根工字型加固撑进行加强。闸门工作方式为动水启闭。弧形钢闸门的结构形式如图1所示。

2.2 有限元模型的建立

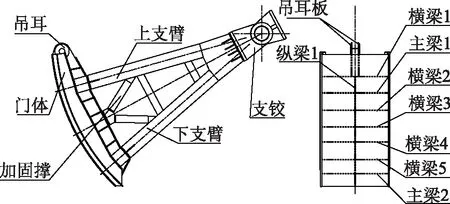
图1 弧形闸门结构示意图

有限元法的本质是建立被研究目标受力特征的有限单元模型，以边界条件为初始值求解有限元偏微分矩阵方程组。目前弧形钢闸门有限元分析计算通常采用四种计算模型：板梁结构、局部壳结构、完整壳结构以及实体结构[8]。梁单元壳单元计算方式计算效率较高，资源占用率低，缺点是壳单元建模的步骤较繁琐，效率很低，只适用于结构形式简单的弧形钢闸门。因此本文采用实体单元构建弧形钢闸门有限元模型进行校核，并在几何建模过程中对部分特征(止水橡皮、螺栓孔等)进行简化。因SolidWorks采用了尺寸驱动的建模方式，建模速度较快，经作者统计其模型完成时间为6h左右，直接保存为STEP格式导入ANSYS Workbench。若采用壳单元则需要在ANSYS Workbench内置的建模工具Design Model中完成面模型并作面分割处理，预估建模时间为14h左右，可见采用实体建模方式效率相对较高。在ANSYS Workbench中对导入的弧形钢闸门STEP模型采用“印记面”方法进行处理，从而使相邻构件间实现接触面共享，保证模型组件间网格的连续性。

选择合适的单元和网格划分形式是建立弧形钢闸门离散化空间结构有限元模型的重要过程。为反映弧形钢闸门实体结构的特性，面板、主梁、横梁、吊耳板以及上下支臂腹板翼板等规则结构板件使用八节点六面体实体单元Solid185，支铰等不规则构件使用Solid185单元退化后的四节点四面体形式，相邻构件间采用节点绑定(MPC)约束以实现节点间力的传递。

2.3 设置材料参数

弧形钢闸门的门体与支臂的主要材料为Q235B钢板，厚度均大于或等于20mm，按照NB35055—2015，材料参数取如下值：弹性模量E=2.06×105MPa，泊松比μ=0.30，密度取7850kg/m3。

2.4 计算工况与边界条件

电站所处位置为浙江天台县，属于地震极少地区，可忽略弧形钢闸门在遭遇地震时横向加速度水锤的作用。按照弧形钢闸门实际的工作状态，校核计算时主要考虑以下两种工况：①静态挡水；②启门瞬间。约束边界条件和载荷边界条件施加方法，①静态挡水工况，约束边界条件如下设置：支铰座底面为固定支承，支铰轴与支铰孔内设置圆柱约束以模拟弧形钢闸门启闭时支铰的旋转作用，两侧边梁止水橡皮安装面设置无摩擦约束限制门体横向自由度，两个吊耳孔内施加竖向约束。载荷边界条件设置为：根据闸门设计水头在弧形钢闸门面板上施加静水压力，设置重力加速度9.8m/s2以施加弧形钢闸门自重载荷；②启门瞬间工况：以工况1的约束边界条件和载荷边界条件为基础，两个吊耳孔去掉Y方向竖向约束后分别施加弧形钢闸门提升方向的启闭力315kN，力矢量方向为Y轴正向，弧形面板底缘施加无摩擦约束，以模拟启门瞬间底缘的吸附作用。

3 后处理结果与分析

3.1 安全校核准则

弧形钢闸门门体及支臂主要结构材料为塑性材料，适用于VonMises准则(第四强度理论)进行校核，第4强度理论计算公式为：

≤[σ]

(1)

式中，σ1、σ2、σ3—结构件任意位置积分点处三个方向的应力分量。

ANSYS Workbench计算出某积分点处应力分量，根据以上公式计算出的应力σv即称之为结构件某个积分点处的综合VonMises应力。

根据NB35055—2015要求，采用Q235B钢板作为构件制造材料的弧形钢闸门许用应力见表1。

表1 Q235B钢制闸门许用应力

考虑到弧形钢闸门的工作安全性以及在较长的使用时间后主要构件有可能出现腐蚀引起的板厚减薄因素，NB35055—2015要求弧形钢闸门的许用应力要根据其重要程度和工作工况强度情况取应力调整系数[9]，通常在0.80～0.95之间。对于使用较长时间的弧形钢闸门，在应力校核时要根据SL101—2014《水工钢闸门和启闭机安全检测技术规程》，按照投入使用时间的长短取时间调整系数，通常在1.0～0.90之间。该弧形钢闸门为中型水利工程的工作门，投入使用时间为16a，两种系数均取0.95，最终许用应力折减系数为两者乘积，经折减处理后的弧形钢闸门许用应力见表2。

表2 折减调整后的Q235B钢制闸门许用应力

根据表2，当弧形钢闸门所有构件大部分区域的σv小于等于Q235B钢折减后抗拉抗压和抗弯许用应力[σ]，弧形钢闸门即可评估为强度合格。另外NB35055—2015规定潜孔式工作闸门和事故闸门的主梁的最大挠度与计算跨度的比值不应超过L/750(L为闸门门体横向跨度)，弧形钢闸门门体宽度为2000mm，因此门体的最大挠度不应超过2.667mm。ANSYS Workbench中根据载荷边界条件对有限元模型求解出的节点变形进行数学处理后得到的值称之为位移(Displacement)，若弧形钢闸门的门体和支臂位移小于2.667mm，那么弧形钢闸门即可评估为刚度合格。

3.2 支铰及吊耳约束的反力

求解完成后，在后处理中提取弧形钢闸门有限元模型的约束反力和综合VonMises应力，弧形钢闸门门体在静态挡水工况下，单支臂支铰座的反力为4.73×106N，反力方向矢量穿过支铰轴指向门体，反力值与门体施工图标注的面板设计总水压力4600kN非常接近，说明施加的载荷边界条件和约束边界条件完全符合弧形钢闸门在工作状态下的真实受力情况。在启门瞬间工况，支铰座反力增大至5.15×106N，支铰座反力增大的原因是弧形钢闸门在启门瞬间由于面板底缘的吸附作用，吊耳上的启门力在两处支臂杆上的分力小幅度增大导致支铰座处的反力增加，可见启门瞬间是弧形钢闸门结构受力不利的工况。

3.3 VonMiese应力结果

静态挡水工况下，弧形钢闸门综合VonMises应力及变形分布，门体构件以及支臂构件大部分区域的综合VonMises应力小于125 MPa，小于Q235B钢折减后抗拉抗压和抗弯许用应力，钢闸门在静态挡水工况下强度评估合格。部分结构件相接触边缘出现局部应力集中，如弧形钢闸门门体底缘处，靠近主梁2下方的纵梁1后翼板边缘与面板接触部位，其综合VonMises应力达到220.18MPa，虽然该处的综合VonMises应力超过了表3中Q235B钢折减后局部承压最大许用应力，但ANSYS Workbench在求解实体单元构成装配体的有限元模型时，个别相邻构件的几何边缘难以避免出现局部应力集中的情况，若该处的应力在合理范围内且局部应力集中部位并非重点关注构件，通常将该局部应力集中作为“应力奇异点”而舍弃。另外根据圣维南原理，结构件几何突变部位的局部应力集中不影响构件的整体受力状态，Q235B钢为塑性材料，塑性材料受荷载后局部应力集中会因结构产生局部塑性变形而大大缓解，因而局部应力集中对整体结构安全性不会产生影响。

主横梁作为最主要的承力构件，分担面板的水压力并传递至支臂。在静态挡水工况下，主梁1及主梁2腹板横向的综合VonMises应力分布如图2所示。

图2 挡水工况闸门主梁1应力变化曲线

主梁1及主梁2的综合VonMises应力不超过40.0MPa，其应力分布特点是主梁两端靠近边梁处综合VonMises应力较小，最大综合VonMises应力出现在主横梁从竖向中心面向左右各0.5m长度的位置。主梁1及主梁2构件的综合VonMises应力小于表2中Q235B钢折减后抗拉抗压和抗弯许用应力，因而其强度评估合格。中纵梁被主梁1及主梁2分隔为上中下三段，上段兼做吊耳板，在静态挡水工况，主梁、横梁以及面板承担了大部分水压载荷，中纵梁分担水压载荷相对较少，纵梁腹板综合VonMises应力不超过78MPa，主梁1后翼缘与中纵梁腹板发生挤压而出现局部应力集中，局部应力集中处的最大综合VonMises应力为91.62MPa，小于表2中Q235B钢折减后抗拉抗压和抗弯许用应力，其强度评估合格。

上下支臂构件直接承受来自门体的水压力，从图2计算结果来看，上下支臂的综合VonMises应力靠近门体连接处偏低，沿支臂轴向朝着支铰方向综合VonMises应力逐渐增大，在靠近裙板处达到最大值，其中上支臂的综合VonMises应力明显高于下支臂，因而上支臂的结构强度较为重要，在设计中要仔细考虑。

图3 静态挡水工况闸门上下支臂应力变化曲线

在启门瞬间工况，弧形钢闸门门体的应力及变形，其综合VonMises应力分布状况与静态挡水工况下应力分布状况相比没有明显变化，最大综合VonMises应力出现在上支臂翼板下方，靠近支臂间工字型加固撑翼板以及后方的工字型加固撑翼板相交区域，属于局部应力集中现象，不影响整体结构强度。但上支臂两侧腹板的最大综合VonMises应力比静态挡水工况下计算结果增大13.2%(静态挡水工况110.2MPa，启门瞬间工况124.8MPa)，经分析认为，上支臂构件出现综合VonMises应力增大的原因是启门瞬间因泥沙和水流在门体底缘的吸附作用，启门力在上支臂处的分力增大而导致。虽然上支臂构件在两种工况下的综合VonMises应力小于表2中Q235B钢折减后抗拉抗压和抗弯许用应力，但因上支臂相对下支臂受力较大，在与本文相同类型弧形钢闸门的支臂设计中，应考虑增大上下支臂杆件截面的抗弯截面系数以提高其承载能力。

3.4 结构位移计算结果

弧形钢闸门整体位移特性以门体与支臂前端向水流下游方向平移为主。在静态挡水工况，弧形钢闸门结构最大位移值为4.309mm，最大位移值出现的位置为面板顶部边缘两侧。弧形钢闸门门体竖向构件纵梁1、边梁1、2，与横向构件主梁1、2、横梁1～5构成门体的主要承力结构，并将面板分成16个区格，由于区格中央和面板顶部边缘以及底部底缘没有承力构件，因此在门体承受总水压力4600kN状态下，面板各个区格中央因水压力作用呈现“凹陷”状态，同时面板顶部边缘以及底部底缘也因凹陷外加门体受水压作用向水流下游平移，因而面板底部底缘出现最大位移值。除面板顶部边缘以及底部底缘外，面板其他区格中央变形较小。水压力通过面板作用在各个主梁、横梁等构件上，主梁横梁的变形以横向弯曲为主。主梁1、2左右两端位移值为2.47mm，中心为2.39mm，其挠度为0.08mm；横梁1- 5的挠度分别为0.08、0.04、0.06、0.05、0.03mm；纵梁吊耳板顶部位移值为2.83mm，底部位移值为2.33mm，门体整体横向挠度和高度方向挠度不超过1mm，门体自身变形很小。从侧面看，上下支臂与门体构成三角受力结构，门体将水压力传递至支臂的端部，导致上下支臂向支铰方向移动，上下支臂最大位移出现在上下支臂前端与门体连接的法兰处，其值为2.39mm。

在启门瞬间工况，弧形钢闸门门体及支臂的位移趋势以及最大位移出现位置与静态挡水工况计算结果相同，由于吊耳处启门力的作用，闸门门体顶端位移值略高于静态挡水工况下的位移值，底缘处位移值则略小。启门瞬间工况弧形钢闸门结构最大位移值为5.011mm，比静态挡水工况大0.7mm。主梁1左右两端位移值为2.89mm，中心2.81mm，挠度0.08mm、主梁2左右两端位移值为1.84mm，中心为1.74mm，挠度为0.10mm；横梁1- 5的挠度分别为0.07、0.03、0.06、0.06、0.06mm；纵梁吊耳板顶端位移值为3.69mm，底部位移值为1.59mm。门体横向挠度不超过1mm，纵向挠度2.1mm。在启门工况上下支臂最大位移值为2.64mm，最大值出现在上支臂前端与门体连接的法兰处，下支臂前端与门体连接法兰处的位移值为1.67mm，可见由于吊耳启闭力和门体面板水压力复合作用下，上支臂的位移值大于下支臂的位移值。门体及支臂在两种工况下的最大位移值小于NB35055—2015要求的最大挠度，弧形钢闸门的刚度评估合格。

4 门体底缘局部应力集中原因分析与优化

在静态挡水和启门瞬间两种工况下，由于弧形钢闸门门体竖向构件只有中心的纵梁1以及两侧的边梁1、2，纵梁与边梁之间相隔1.0m，在水压力作用下，门体主梁2下方与纵梁1交界形成的面板区格底缘处缺少支撑，因此该处的位移值相对纵梁构件较大(区格中心下边缘3.37mm，纵梁中心2.3mm)。另外，面板底缘与下纵梁的后翼板相互接触，当门体面板底缘出现变形时，面板底缘与下纵梁的后翼板彼此挤压，因而在下纵梁后翼板边缘尖点处出现局部应力集中。虽然局部应力集中部位为非关键部件，对整体安全性没有影响，但因面板底缘结构布置不合理，需进行结构优化以消除局部应力集中。采取局部补强方式，在面板底缘处增加2块加强板，避免面板底缘与下纵梁后翼板端部局部挤压。底缘设置加强板后，以静态挡水工况为边界条件再次进行有限元分析，计算结果表明下纵梁后翼板的局部应力集中完全消除，由原来的220.18MPa降低至73MPa，局部变形也基本消除。

5 结论

本文基于ANSYS Workbench建立了弧形钢闸门的有限元模型，求解并分析了弧形钢闸门在静态挡水和启门瞬间两种工况下支铰座反力变化情况，结构整体及主要承力构件的综合VonMises应力与位移的分布规律与变化情况，依照NB35055—2015评估了弧形钢闸门的安全性，分析了弧形钢闸门面板底缘局部应力集中的原因并对底缘结构进行优化。形成如下结论。

(1)弧形钢闸门在静态挡水和启门瞬间两种工况下，门体与支臂构件的强度及刚度评估合格，启门瞬间支铰座支承力增大，因而启门瞬间是弧形钢闸门受力最为不利的情况。

(2)构建实体几何模型，导入ANSYS Workbench建立实体有限元模型的方法效率较高。

(3)对于单支臂形式的弧形钢闸门，在启门瞬间工况，上支臂构件最大综合VonMises应力要比静态挡水工况增大13.2%，建议在同类型弧形钢闸门设计阶段，应考虑同时加大上下支臂的抗弯截面系数以改善支臂构件的受力情况。

(4)对于实体单元构建的装配体有限元模型，非关键部位因相邻构件几何边缘相互挤压引起的局部应力集中对整体结构安全性没有影响，通过局部补强的方式能够有效降低或消除局部应力集中。