基于拓扑方法的汽车车体结构优化
2020-07-01斉藤孝信塩崎毅玉井良清
【日】 斉藤孝信 塩崎毅 玉井良清
0 前言
出于环保及改善燃油耗的需求,各大车企正在快速推进汽车车体的轻量化。为实现轻量化,汽车白车身更倾向于使用高强度钢板。随着高强度钢板的应用,相应降低了板材厚度,使整个车体的刚度也随之降低。作为相关对策,使用质量最轻的材料以弥补由此降低的刚度是必不可少的。目前,可通过拓扑学最优化方法实现改良[1-2]。拓扑学最优化方法是在给予一定设计空间的前提下,保留所必备的单元。通过拓扑学最优化设计,可将复杂而独特的形状应用于零部件。该方法目前已在发动机缸体及悬架下控制臂等领域的最优化过程中得到应用。
就由薄板构成的车体而言,由于拓扑学最优化过程中须重点考虑单元尺寸及计算负荷等问题,不能使单元尺寸过度缩小[3],所以运用拓扑学最优化方法难以设计出具体的零件形状。基于初步的设计指南[3-4],研究人员针对目前车体结构中灵敏度较高的部分,对薄壳单元实现了拓扑学最优化处理[5-6]。
本文介绍了在由薄壳单元组成的汽车车体结构中,引入由实心单元构成的设计空间,使用拓扑学最优化方法以改善零部件形状[7-9]。此外,介绍了拓扑学最优化分析程序在点焊中的应用,以及针对粘结剂涂覆位置最优化过程的示例[10]。
1 使用了白车身的静态刚度的零件形状最优化
1.1 分析方法

图1 最优化过程中使用的整车模型
图1表示用于白车身最优化过程的整车模型。该整车模型由美联邦新车评价中心(NCAC)所公布,车体由薄壳单元所构成。图2示出了车体承载负荷的4个约束条件。约束前悬架安装部件与后部螺旋弹簧安装部件共占4个条件中的3个,剩下1个负荷条件是在车辆上方加载1 000 N负荷。同时,科研人员设定了变更负荷加载位置的4个条件,使用了图1所示的白车身,对在由薄壳单元构成的车体中采用的空间设计方法的合理性进行了验证。目标部件被设定为在灵敏度分析中用于构成后部地板的侧构件与横向构件的结合部分。图3示出了最优化的目标部件。在设计空间的引入过程中,科研人员去除横向构件的终端部件,从而对由实心单元构成的设计空间进行了布置。考虑到负荷的传递需求,将通过实心单元构成的设计空间与通过薄壳单元构成的横向构件的端部、后部侧构件,以及地板进行了连接。最优化的目标条件是使图2所示的4个负荷条件的平顺性总和最小。约束条件还应考虑到在设计空间内通过薄板生成零件的形状,将其体积百分率设定为20%。此外,研究人员充分运用基于拓扑学最优化方法的保留结果,优化了零件形状,进而确保了其刚度。

图2 扭转刚度的负荷约束条件

图3 最优化过程的目标部件
1.2 最优化结果
图4示出了车体经拓扑学最优化处理后的保留部分。该保留部分由后部侧构件与横向构件所组成,重点保留了设计空间的地板侧平面。通常认为应从加载点通过侧构件、横向构件向地板传递负荷。

图4 拓扑学最优化过程后的保留结果
1.3 基于最优化结果的形状研究
图5表示了运用基于拓扑学最优化方法而生成的新零件与原零件的形状对比。最优化后的零件与原零件同样用点焊连接了侧构件、横向构件和地板。以原零件为基准,经最优化处理后的零件的抗扭刚度提高约4.3%,质量增加了0.1 kg。在通常情况下,提高车体扭转刚度具有较高难度。研究人员从质量效率的观点出发,认为通过该方法能实现抗扭刚度的最优化(指能以最小的质量增加为代价而强化零件刚度)。

图5 零件原有形状与经最优化后的形状
图6通过应变能分布情况的对比,以说明零件最优化后的效果。在该最优化实例中,可使零件平顺性的总和降至最低。原零件中横向构件的边线及地板的边角位置均产生了较大的应变能。由此确认,经最优化处理后的横向构件的边线及地板边角位置的应变能均已大幅降低。

图6 零件应变能分布情况的对比
2 白车身特征值的零件形状最优化
2.1 分析方法
图7表示运用了计算机辅助工程(CAE)的特征值分析而得出的车体前部弯曲变形的状态。作为本次研究的对象,选择了仅在车体前部沿车宽方向进行移动的前部弯曲模式。车体全长为4 178 mm,用25倍表示了其变形情况。根据图7可知,车体仅会面临前部弯曲的状态。从该弯曲模式的特征值看,原车体弯曲特征值为31 Hz,操纵安全性较好的车体的前部弯曲特征值会在40 Hz以上。因此,研究人员将比40 Hz更高的数值作为目标而开展研究。

图7 基于前部弯曲变形状态的特征值分析
对图1所示的白车身,通过在由薄壳单元构成的车体上引入空间设计的方法,建立了最优化模型。优化过程的目标部件被设定为前部横向弯曲区域内从散热器固定架到发动机上部的前侧部分。图8(a)示出了原车体状态;图8(b)表示从原车体去除了零件后的状态;图8(c)表示将由实心单元构成的设计空间引入至全车模型后的状态。对于去除了散热器固定架及翼子板支架而保留了前构件的车体而言,配置了通过实心单元构成的设计空间。此外,考虑到负荷传递需求,连接了设计空间与车体,设定了最优化的目标条件,使前端弯曲特征值最大化,并设定了其体积百分率应为20%以下。作为对性能的验证,运用经拓扑学最优化后的保留结果,生成了断面形状各异的模型,同时调整了其形状及板厚,进而验证了特征值。另外,作为技术对比,对用于固定保险杠的塔形支撑杆进行了验证,并将基于灵敏度分析而设计出的零件作为优化目标,对通过增加板厚而改善了特征值的情况进行了验证。

图8 引入了实心单元的车体模型
2.2 最优化结果
图9表示利用车体模型进行拓扑学最优化后保留的状态。保留特征的结果是前侧部分呈现X形。先在散热器固定架附近实现一次性收缩,然后与保险杠左右安装部相连接,再次在车体下部收缩,从而得出了保留后的状态结果。从该结果可知,为提高前部弯曲的特征值,通过连接部件而支承前部悬架及保险杠的方案是卓有成效的。

图9 利用车体模型进行拓扑学最优化后保留的状态
2.3 基于最优化过程的零件形状研究
将经最优化后设计出的零件配装到车体上,同时作为与最优化零件的比较,采用了连接左、右悬架的塔形支撑杆。图10示出了经灵敏度分析后增加了板厚的零件。将这些零件的板厚同样按1.2倍、1.4倍、2.0倍分别设定,并进行了特征值分析。图11同时示出了使用塔形支撑杆、增加板厚,以及通过形状最优化处理后的零件前部弯曲特征值。经最优化处理后的零件的前部弯曲特征值为55 Hz,该类值得以大幅提高。将塔形支撑杆的特征值增加0.2 Hz,对于前部弯曲部件而言,特征值的增加尚无法起到明显效果。此外,即便只增加高灵敏度零件的板厚,如以增加25 kg的板件质量为例,其特征值也只能提高到35 Hz,其效果无法与最优化过程相比。
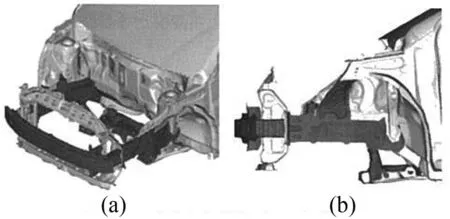
图10 增加了板厚的零件

图11 形状最优化后的零件特征值
3 白车身点焊焊接点位置的最优化
3.1 分析方法
图12示出了点焊焊接点最优化程序的示意图。该图模拟了零件凸缘部,是按20 mm间隔设定补加焊接点的示例。原焊接点按40 mm间距进行布置,优化后按最小20 mm间距将其设定为最优化过程的目标焊接点。根据拓扑学最优化方法,只保留了对刚度有较大提升效果的焊接点。
在整车模型中,按照10 mm、20 mm、30 mm分别调整最小焊接点间距,研究了其对刚度的影响。整车模型使用了图1所示的车体,负荷条件则使用了图2的抗扭刚度负荷约束条件,并通过实心单元描述了焊接点。相比车体上原设定的3 906个焊点,按最小20 mm的焊接点间隔,设定了最优化后的目标焊接点数为3 168个;按最小10 mm的焊接点间隔,设定了最优化后的目标焊接点数为10 932个;按最小30 mm的焊接点间隔,设定最优化的目标焊点数为1 679个。将上述焊接点设定为后续开展拓扑学最优化过程的目标条件,使4个负荷条件的平顺性总和最小,使其为刚度最大的约束条件,从而保留了焊接点数与最优化焊接点数的比例。最优化过程后保留的焊接点数都按最小焊接点间隔分别设定为200个、400个和600个。此外,使用了基于拓扑学最优化过程的保留结果,生成整车模型,并通过CAE验证了其刚度。
此外,在具有高应变特性的焊接点附近补加了其他焊接点,与最优化后的结果进行了比较。图13示出了通过传统方法补充焊接点的示意图。采用的方法是在应变能较大的焊接点两侧间距20 mm的位置上各补加2个焊接点。在上述4个负荷条件下的各个焊接点上,按照应变能总和大小进行排序,将目标焊接点数设定为100个。在这100个目标焊接点的两侧,按最小20 mm的间距补加了200个焊接点。
3.2 焊接点位置的最优化分析结果
图14示出了在整车模型的各个最小焊接点间隔条件下,基于拓扑学最优化过程后保留的焊接点。这是在各种焊接点间隔条件下均补充200个焊接点的结果。保留焊接点的位置主要分布于后部横向构件(后横梁),车身B柱上、下部,A柱及减振器塔形支撑件周边。此外,在焊接点间距较小的情况下,可看到保留的焊接点呈现密集分布的趋势;在焊接点间隔较大的情况下,可看到保留的焊接点呈现分散的趋势。

图12 补充焊接点的最优化过程示意图

图13 通过传统方法补充焊接点的示意图

图14 基于拓扑学最优化过程而保留的焊点
图15表示运用拓扑学最优化过程,通过补充焊接点以提高车体刚度的效果。在所有最小焊接点间隔的条件下(指焊接点间距分为别为10 mm、20 mm、30 mm),随着焊接点数的不断补充,刚度有所提高。但当焊接点间距为30 mm时,随着焊接点数的增加,刚度提高效果逐渐趋于饱和。另外,在同样补充焊接点的条件下,焊接点间隔越小时刚度提高效果越明显。此类现象是由于10 mm的焊接点间隔较小,所以能可靠地设定有利于提升刚度的焊点位置;在焊接点间隔为30 mm的条件下,由于受焊接点间隔的制约,通常无法直接提升部件的刚度。

图15 利用最优化过程补充焊接点以提升车体刚度的效果
图16表示分别通过传统方法与拓扑学最优化方法补充200个焊接点位置后的效果比较。通过传统方法补充的焊接点位置集中于后方横向构件及车身B柱的上部和下部,而通过拓扑学最优化方法追加的焊接点基本分布于整个车体上。图17表示采用传统方法及拓扑学最优化方法,通过补充点焊焊接点以提高刚度的效果。采用拓扑学方法的刚度提升效果比采用传统方法的刚度提升效果要高出3倍。这可认为是初期通过传统方法决定后续焊接点的位置,但却无法适应补充焊接点过程中的应变状态所导致的。另一方面,在拓扑学方法应用过程中,认为补充的焊接点位置已得以最优化,以便在补充200个焊接点时使刚度达到最大。

图16 补充焊接点的位置比较

图17 利用补充焊接点的方法以提高刚度的效果对比
4 白车身结构用粘结剂涂覆位置的最优化
4.1 分析方法
至于针对粘结剂涂覆位置的最优化,使用了图1所示的白车身模型,负荷条件则与焊接点位置最优化过程相同。在整车模型方面,根据在凸缘面上涂覆粘结剂的状态,运用了拓扑学最优化方法,调整保留量,研究了其对刚度的影响。粘结剂通常被设定为实心单元,设定了涂覆全长为103 m的结构用粘结剂。由于前后保险杠部、车顶部、副车架等部件并非粘结剂的主要应用部位,因此通常不被计入研究目标。
研究人员将应用粘结剂的部位设定为拓扑学最优化过程的目标条件,以使4个负荷条件的平顺性总和最小。为使刚度达到最大,在制约条件方面使用了保留的粘结剂量/以最优化为目标的粘结剂用量的比例参数。经最优化过程后保留的粘结剂的比例分别设定为80%、60%、40%和20%共4种情况。此外,运用基于拓扑学最优化过程的保留结果,构建整车模型,测量了凸缘长度方向上粘结剂的涂覆长度,并对刚度进行了验证。依据粘结剂的特性,研究过程中所使用的弹性模量为3.0 GPa,泊松比为0.45,比重为1.0,并通过CAE验证了其刚度。
研究人员利用CAE精确地构建了结构模型。但在使用粘结剂的情况下,该过程对人工操作依赖性较高,因而耗费了较多工时。因此,针对焊接点位置的最优化过程,重点研究了通过调整粘结剂涂覆位置以提高刚度的方法。由于能实现自动化补充焊接点,因此可使工时降至原来的50%以下。运用图12所示焊接点的最优化程序,采用10 mm的焊接点间隔,对接合单元进行了配置,以使其形成接近于连续接合的状态。此外,要求接合单元与粘结剂的最优化过程相一致,保留原有的焊接点。至于整车模型,相比于车体上原有的3 906个焊点,研究人员设定了最优化后的目标焊接点数为10 932个。为使4个负荷条件的平顺性总和为最小,保留了3 600个接合点。通过这一保留结果,开展了针对粘结剂涂覆位置的研究。
4.2 粘结剂涂覆位置的最优化分析结果
图18表示在整车模型上使用了拓扑学最优化方法后的粘结剂保留位置。主要保留的涂覆位置为后部横向构件(后横梁)、车身B柱上下部、A柱、减振器塔形支撑件周边及前围板。

图18 通过拓扑学最优化并采用结构粘结剂后保留的涂敷位置
应用基于焊接点位置的最优化方法,为了重点研究有利于提高刚度的粘结剂涂覆位置,比较了通过拓扑学最优化方法而补加的600个焊接点与采用粘结剂涂覆的位置。图19示出了这些焊接点与采用粘结剂涂覆后的最优化位置。保留焊接点的位置主要为后部横向构件,车身B柱上下部,A柱及减振器塔形支承件周边区域。与粘结剂保留的位置相比,两者分布位置大致相同。如前围板及车身后侧围板上部,则是焊接点保留较少的部位。

图19 焊接点与涂覆粘结剂的最优位置
另一方面,通常认为粘结剂在焊接点分布致密的区域可充分发挥成效。图20表示了焊接点间隔低于20 mm的部件,以及焊接点间隔大于20 mm并适于涂覆粘结剂的部件。由于该方法的应用,相比于图19中间距较大的位置,由此也显示了离散焊接点的保留结果,并认为其能作为连续接合的粘结剂的应用部位(即明确指出粘结剂涂覆位置)。

图20 结构粘结剂的推荐涂敷位置
图21表示将本方法应用于汽车车体量产的实例。车体为插电式混合动力汽车(PHEV)Edition车型的车体。在该车型后车门开口位置及货厢后栏板的开口位置、轮罩部等处通过拓扑学方法进行优化,并涂覆了粘结剂。
5 结语
本文介绍了拓扑学最优化方法在汽车车体中的应用。就以薄板构成的车体而言,采用由实心单元构成的设计空间,运用拓扑学最优化方法,可实现零件形状的最优化并加强零件的最优化配置。这种方法在负荷传递路线复杂的全车模型领域,能设计出质量较高的零件形状。此外,拓扑学最优化方法对于焊接点位置及粘结剂涂覆位置的最优化也有着较好效果。同时,通过整车模型能有效优化焊接点位置及粘结剂涂覆位置。今后,可逐渐扩大拓扑学最优化方法的应用领域。

图21 针对量产车的结构粘结剂应用示例
