环境风对跳台滑雪空中飞行气动特性的影响

胡 齐，刘 宇

（1.国家体育总局体育科学研究所，北京 100061；2.上海体育学院 运动科学学院，上海 200438）

跳台滑雪过程通常分为4个阶段：助滑、起跳、飞行和着陆，而且主要涉及弹道学和空气动力学两大方面，两者都对跳台滑雪运动员提出了特殊的要求，如应最大限度地提高升力并且减小阻力。弹道学因素包括运动员从跳台上起跳位置和速度，空气动力学因素包括运动员/滑雪板多体系统的气动特性，即速度、姿态、环境风、服装和滑雪板长度等（胡齐等，2018b）。在运动员助滑起跳后，在飞行阶段早期应尽快达到一个稳定的飞行位置，并完成向后和向前旋转角动量的完全平衡（Schwameder，2008），同时确保受到较小的阻力（Murakami et al.，2010）。飞行阶段被认为是跳台滑雪过程气动特性体现最为明显的阶段，不少研究人员采用风洞实验测量或计算机模拟与现场测量相结合等方法进行了飞行阶段气动特性相关研究（王志选 等，1998；Jung et al.，2014；Murakami et al.，2014；Schmolzer et al.，2005；Virmavirta et al.，2005）。为能直观地显示或分析运动员周围的流场，计算流体力学（computational fluid dynamics，CFD）是首选的重要技术工具，能够分析在运动过程中气动力、压力分布和详细流场信息等。但迄今为止飞行阶段CFD相关研究较少（陈志峰，2014；胡齐 等，2018a；Lee et al.，2012；Meile et al.，2006；Nørstrud et al.，2009），而且大多重点关注运动员身体姿态，鲜见针对环境风开展研究。Gardan等（2017）通过CFD数值仿真发现，在飞行阶段早期速度对升力系数和阻力系数的影响很小，相反迎风角对运动员升力和阻力的影响很大。Keizo等（2016）采用CFD技术研究了在起跳过程中运动员姿态对气动特性的影响。

研究发现，环境风与跳台滑雪中公平性问题密切相关（Jung et al.，2019），其往往会对飞行距离产生较大影响。在风速为1 m/s情况下，飞行跳跃距离约为130 m的相对得失为4 m（Müller et al.，1996）。从有利方向吹来3 m/s恒定风速，可使185 m的飞行跳跃距离增加16 m，而从不利方向吹来的风速使飞行跳跃距离减少23.7 m（Seo et al.，2004）。为使比赛更公平，赛事能够在不断变化的风下顺利进行，在风洞数据和计算机模拟基础上，国际滑雪联合会（international ski federation，FIS）推出了涉及环境风与助滑跑道的补偿系统（FIS Fact Sheet，2009），即Δω=TWS(HS-36)/20，其中Δω为风对飞行距离（m）的影响，TWS为平均切向风速（m/s），HS为跳台尺寸（m）。应指出的是，在该补偿系统中风速对飞行距离的影响是线性的。Virmavirta等（2012）对环境风补偿系统在跳台滑雪过程中的作用进行了详细验证。但近期有研究人员通过计算机模拟预测，与FIS环境风补偿系统进行比较，发现存在很大差异，例如，在飞行阶段早期，顺风可以增加飞行跳跃距离，逆风可以减小飞行跳跃距离；这与以前的预期相反，在目前环境风补偿系统中也没有考虑到这一点（Jung et al.，2019）。

环境风不仅与跳台滑雪中公平性问题密切相关，而且对跳台滑雪空中飞行安全非常重要。飞行的稳定性是保证跳台滑雪的性能和安全性的关键（Marqués-Bruna et al.，2009），空中飞行稳定性控制主要涉及环境风及飞行姿态等因素，但环境风对空中飞行气动特性以及稳定性的影响尚不清楚，也鲜见相关研究报道。本研究拟建立运动员/滑雪板多体系统的精细化三维模型与网格模型，采用部分时均（partially averaged Navier-Stokes，PANS）湍流模型进行CFD数值仿真，获取不同环境风下力和力矩以及流场形态，分析研究不同环境风对跳台滑雪空中飞行气动特性的影响。

1 研究对象与方法

1.1 研究对象

研究对象为跳台滑雪运动员/滑雪板多体系统。根据Müller等（2006）统计分析结果，跳台滑雪运动员的身体形态特征选取平均值，即身高为177 cm，身体质量指数（body mass index，BMI）为19.5，躯干（坐高）与身高比值0.532，滑雪板长度258 cm，宽11.5 cm。

跳台滑雪运动员在空中飞行的姿态参数包括迎风角φ、滑雪板与速度方向夹角α、滑雪板与身体夹角θ、上半身弯曲角度β和滑雪板夹角λ，如图1所示。本研究中迎风角φ取值为35°、滑雪板与速度方向夹角α取值为35°、滑雪板与身体夹角θ取值为16°、上半身弯曲角度β取值为18°，滑雪板夹角λ取值为28°，速度V取值为29 m/s。图2显示了空中飞行多体系统受力情况。

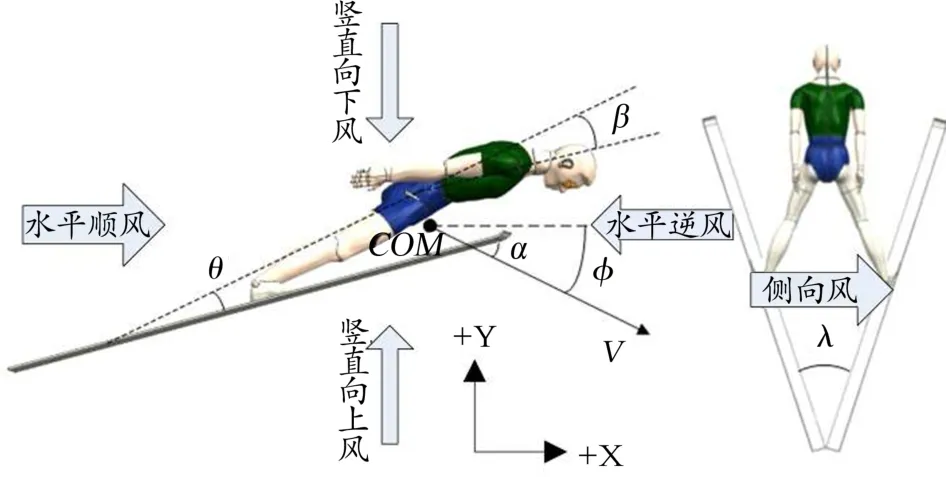
图1 空中飞行姿态参数Figure 1.Attitude Parameters during Flight

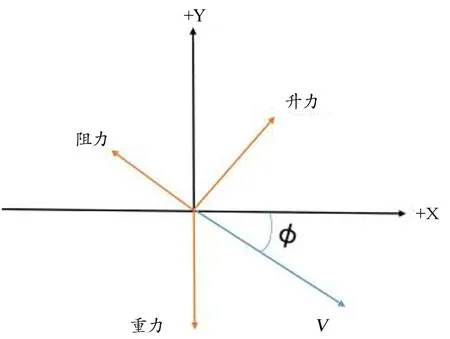
图2 空中飞行多体系统受力情况Figure 2.Forces on the Athlete/Skis System during Flight

1.2 研究方法

1.2.1 控制方程

本研究采用大涡模拟技术，该技术能够更加有效地数值预测钝体周围流动分离情况，已在先前研究中获得了证实（胡齐等，2018a）。为了获得更精确的结果，采用了PANS湍流模型，其控制方程表达式如下：

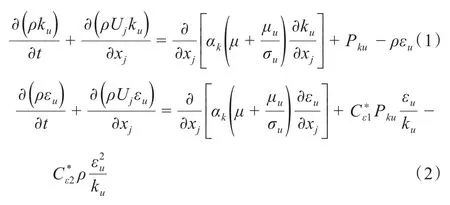
式中Uj为已分解流场速度，t为时间，ρ为流体密度，μ为介质粘性系数，t为湍流粘性系数，fk为未分解湍动能比率，fε为未分解湍动能耗散率比率，ku为未分解局部时均化湍动能，εu为未分解局部时均化湍动能耗散率。

其中：

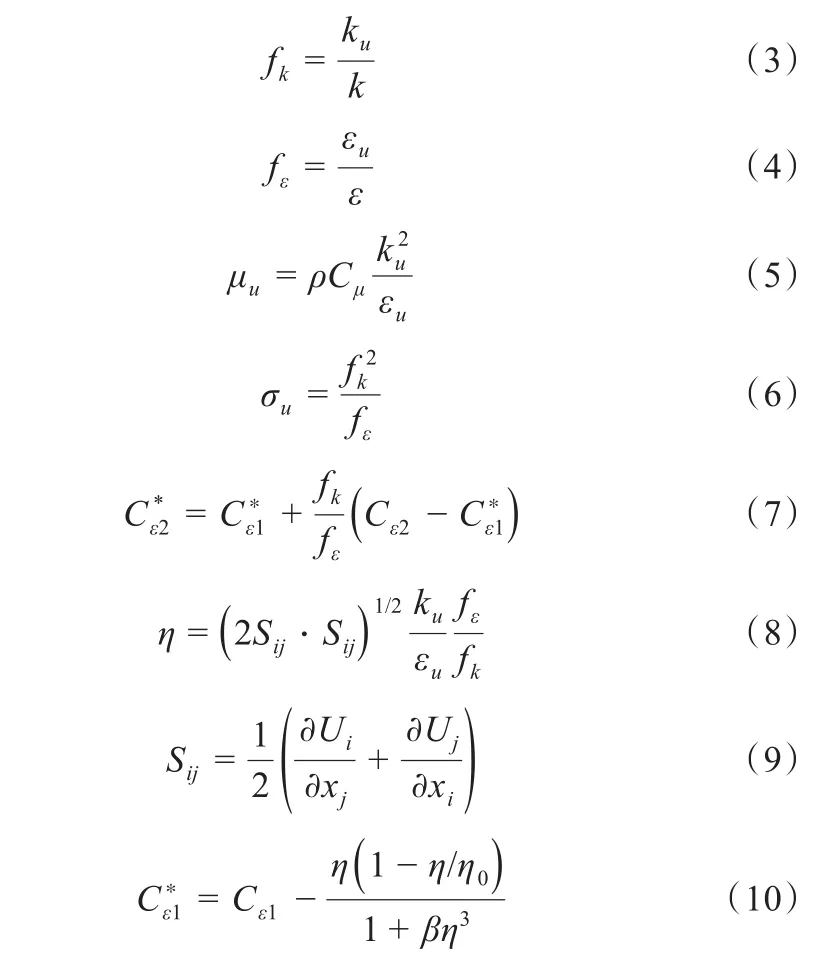
模型中各常数值为：Cμ=0.0845，αk=αε=1.39，Cε1=1.42，Cε2=1.68，η0=4.377，β=0.012。

采用有限体积法对控制方程进行离散计算，压力和速度的耦合采用SIMPLEC算法，时间采用二阶差分格式进行离散，湍动能以及速度项采用二阶迎风格式，时间步长为0.000 1 s。

1.2.2 模型建立与网格无关性验证

根据研究对象结构特征以及选定的空中飞行状态参数，建立跳台滑雪运动员/滑雪板多体系统的三维实体模型，对运动员身体特征进行精细化建模，手指、耳朵、眼罩、面部特征可以从图1中清晰分辨。

跳台滑雪运动员/滑雪板多体系统的计算区域尺寸大小为长18.5 m、宽7 m、高9.5 m（图3）。考虑到尾流存在流动分离以及运动员身体外形特征可能会影响流场等情况，采用商用前处理软件ICEM对跳台滑雪运动员/滑雪板多体系统精细化三维实体模型分区划分网格模型，大致分为运动员身体表面区域、滑雪板表面区域、运动员上臂结合处后侧尾流区域、腰胯结合处后侧尾流区域、运动员其他部位后侧尾流区域、滑雪板后侧尾流区域以及远离运动员与滑雪板区域等。在计算区域中心对称面上体积网格分布和运动员表面网格分布如图4所示，运动员表面网格分辨率最小达到0.5 mm。对于体网格，在运动员周围区域配置了较细的网格单元，以高精度捕获尾流结构。另一方面，为了降低计算量，较粗的网格单元被分配到远离运动员的区域。

为了满足PANS模型计算要求，运动员周边采用网格加密，并保证y plus控制在100之内，此控制要求（Keizo et al.，2016）以及相应的网格划分策略已在先前的研究中（胡齐等，2018a）得到证实。针对上述网格模型，每个分区域选定了4种网格密度，在各自分区域内进行不同程度的均匀加密，网格点数从1 000万至2 838万，进行网格无关性验证，验证结果如表1所示。4种网格验证计算获得的升阻比均在1.95左右。由此可见，即使选定1 000万网格节点的计算域离散方案，也能够准确预测跳台滑雪运动员/滑雪板多体系统的空气动力学性能。

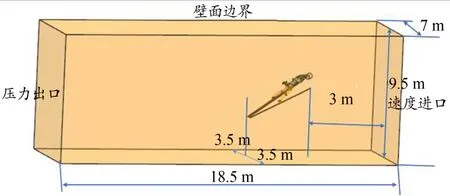
图3 计算区域Figure 3.Computational Domain

图4 网格分布（上面：体网格；下面：运动员表面网格）Figure 4.Mesh Distribution（Above：Volume Mesh；Below：Surface Mesh on Athlete）

表1 网格无关性验证结果Table 1 Results of Grid-independency Test

1.2.3 边界条件与计算工况

边界条件的设置如下：1）进口设置为速度进口，进口速度根据飞行速度设定；2）出口设置为压力出口，压力为大气压101 325Pa；3）中间截面为周期性条件；4）其他壁面为无滑移边界条件；5）气体为不可压缩空气；6）在常重力下，重力加速度设置为g0=9.807 m/s2。

在本研究中，开展了3个不同方向环境风下的跳台滑雪空中飞行气动特性CFD研究，即水平顺/逆风（+X/-X）、竖直上/下风（+Y/-Y）以及侧向风（+Z），如图1所示。本研究依据风力等级对照表选取风速工况，即水平顺/逆风风速工况包括-4 m/s、-2.5 m/s、-1 m/s、0 m/s、1 m/s、2.5 m/s、4 m/s；竖直上/下风风速工况包括-8 m/s、-4 m/s、-2.5 m/s、-1 m/s、0 m/s、1 m/s、2.5 m/s、4 m/s、8 m/s；侧向风风速工况包括 0 m/s、1.5 m/s、3.0 m/s、4.5 m/s、7.5 m/s、10.5 m/s、13.5 m/s。据此，针对每一种风速工况分别进行了CFD数值模拟，提取多体系统的受力及力矩情况，直观地显示多体系统周围的流场信息。

2 结果

2.1 力和力矩

作用于运动员/滑雪板多体系统上的空气动力包括升力和阻力，而且这些力的作用点绝大多数不会在多体系统质心上，因此极有可能会产生相应的力矩。表2～4列出了不同环境风下运动员/滑雪板多体系统的力学特性结果。图5～7显示了运动员/滑雪板多体系统的力学特性随风速变化曲线。结果中各项力均为作用在运动员/滑雪板多体系统或运动员或滑雪板上同一性质的合力。结果中各项力矩为相对于运动员/滑雪板多体系统质心的力矩。俯仰力矩旋转轴为Z轴，“+”代表力矩作用后使多体系统向后仰，“-”代表力矩作用后使多体系统向前倾。偏航力矩旋转轴为Y轴，翻滚力矩旋转轴为X轴。结果中升阻比由升力除以阻力计算得到。

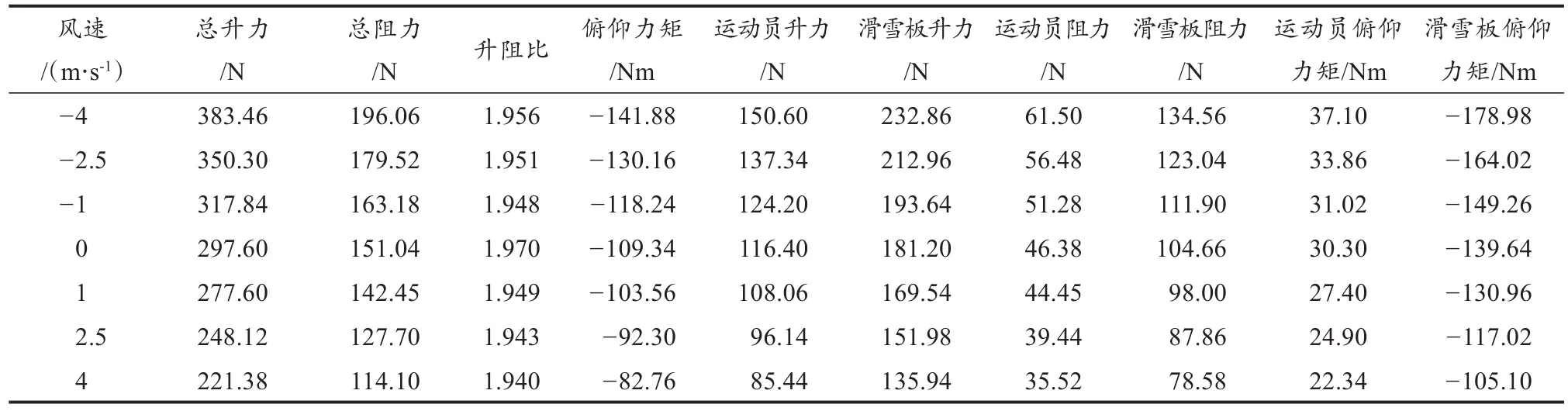
表2 水平顺/逆风工况下力学特性结果Table 2 Results of Mechanical Characteristics under Horizontal Down/head Wind Conditions

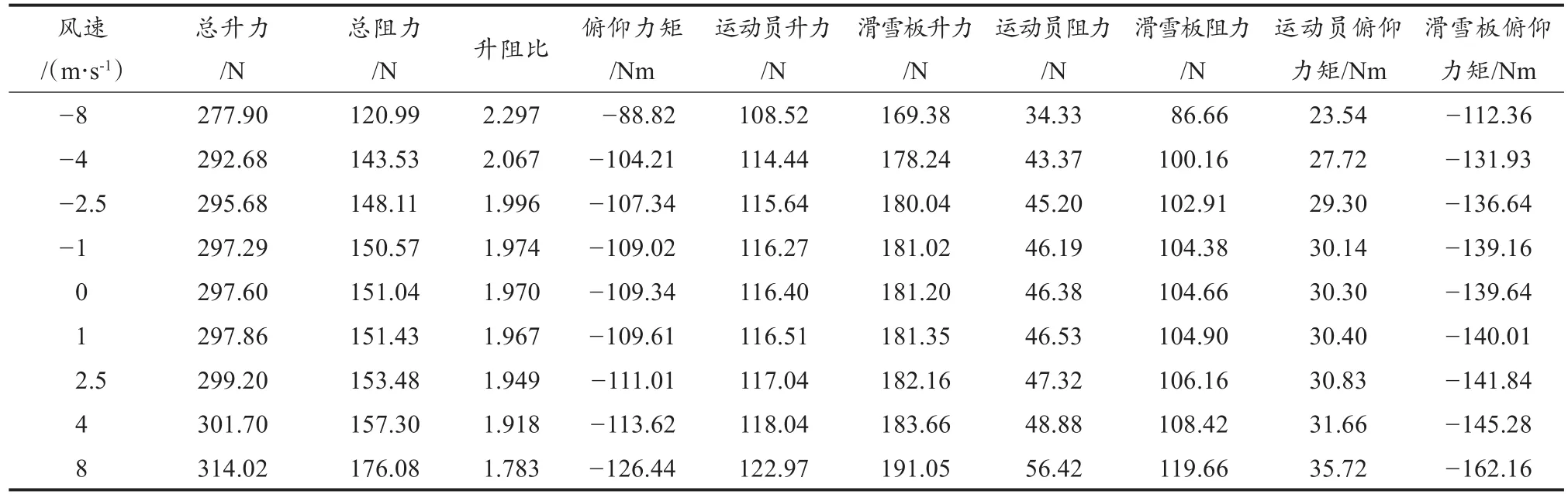
表3 竖直上/下风工况下力学特性结果Table 3 Results of Mechanical Characteristics under Vertical Upper/down Wind Conditions

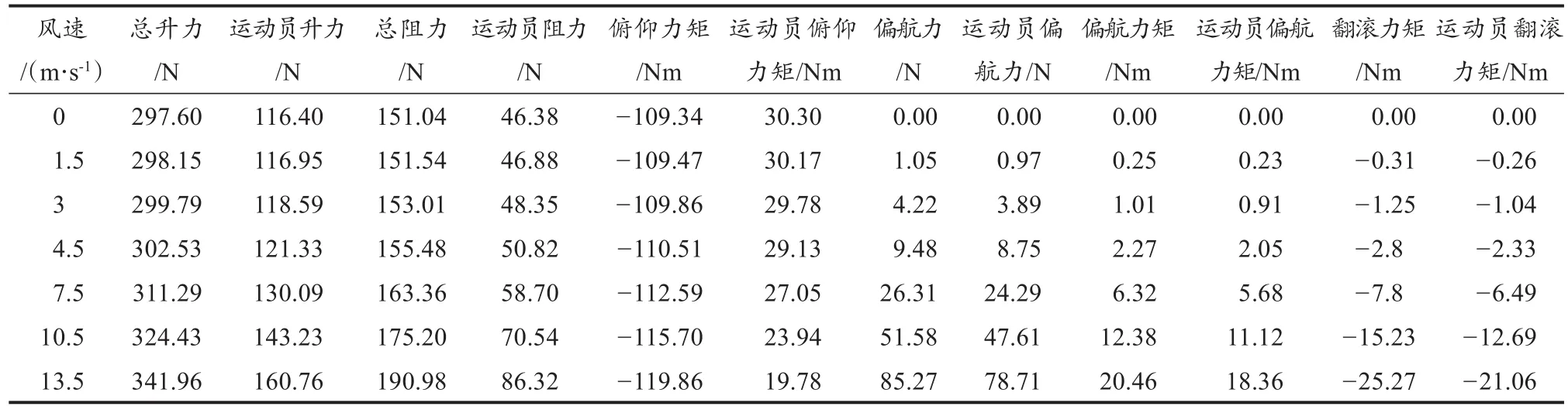
表4 侧向风工况下力学特性结果Table 4 Results of Mechanical Characteristics under Lateral Wind Conditions

水平方向不同环境风下运动员/滑雪板多体系统的力学特性随风速变化曲线如图5所示。可以看出，受水平方向环境风的影响，运动员/滑雪板多体系统、运动员以及滑雪板的升力、阻力以及俯仰力矩数值随着风速增加变化趋势一致，均呈现近似线性单调减小的关系，仅总升阻比基本维持不变。在水平顺风情况下，升力、阻力以及俯仰力矩数值随着风速增加近似线性地单调减小，总升力变化斜率近似-19.9 N/（m/s），总阻力变化斜率近似-9.05 N/（m/s），俯仰力矩数值变化斜率近似-6.41 Nm/（m/s），滑雪板升力变化斜率近似-11.55 N/（m/s），滑雪板阻力变化斜率近似-6.63 N/（m/s），滑雪板俯仰力矩数值变化斜率近似-8.79 Nm/（m/s）；在水平逆风情况下，升力、阻力以及俯仰力矩数值随着风速增加近似线性地单调增加，总升力变化斜率近似21.4 N/（m/s），总阻力变化斜率近似11.6 N/（m/s），俯仰力矩数值变化斜率近似8.25 Nm/（m/s），滑雪板升力变化斜率近似12.69 N/（m/s），滑雪板阻力变化斜率近似7.36 N/（m/s），滑雪板俯仰力矩数值变化斜率近似9.74 Nm/（m/s）。

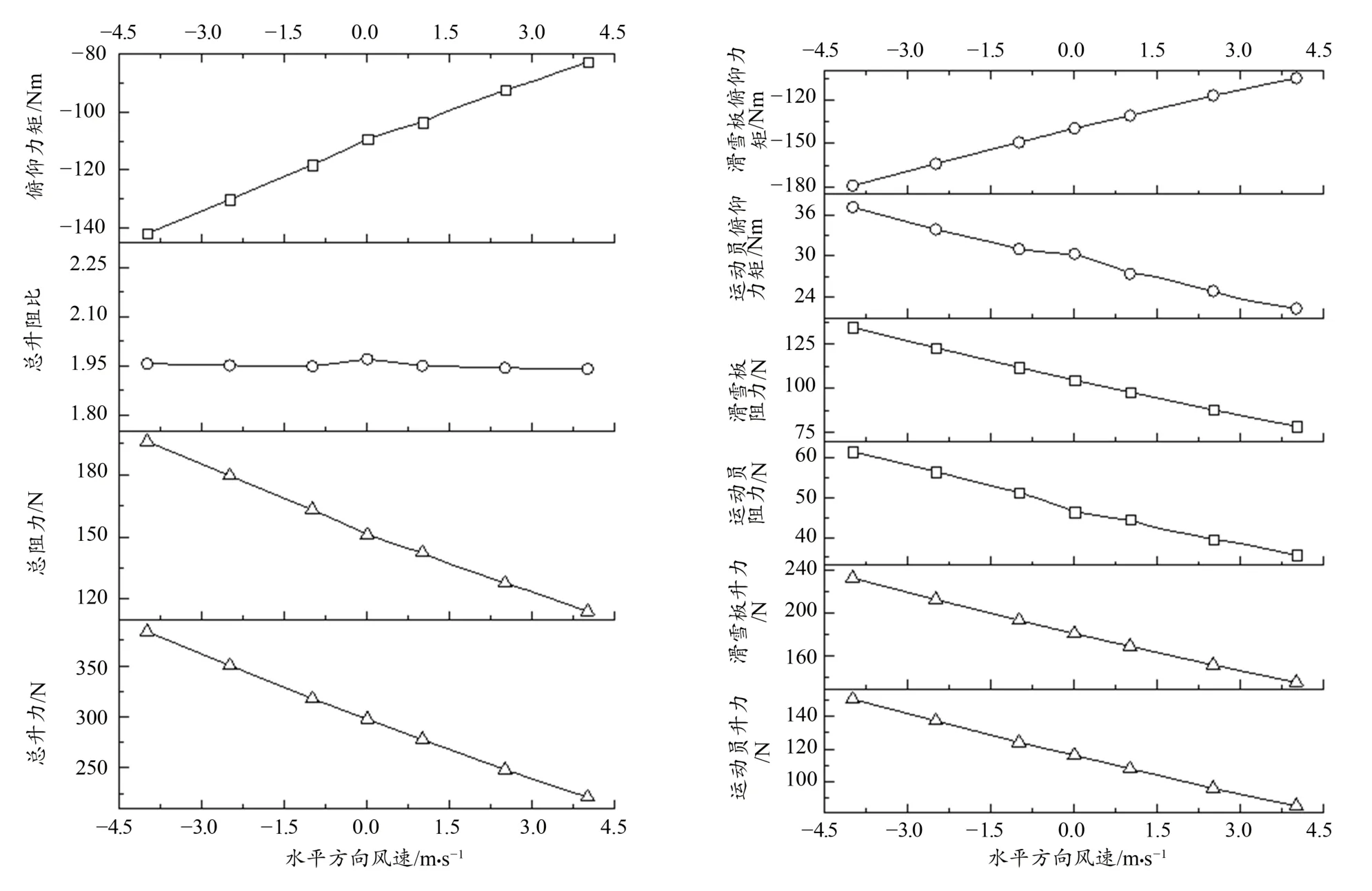
图5 水平顺/逆风工况下力学特性随风速变化曲线Figure 5.Variation of Mechanical Characteristics with Wind Speed under Horizontal Down/head Wind Conditions

竖直方向不同环境风下运动员/滑雪板多体系统的力学特性随风速变化曲线如图6所示。可以看出，受竖直方向环境风的影响，运动员/滑雪板多体系统、运动员以及滑雪板的升力、阻力以及俯仰力矩数值随着风速增加变化趋势一致，均呈现抛物线式凸曲线形式单调增大的关系，但总升阻比呈现抛物线式凸曲线形式单调减小的变化趋势。在竖直向上风情况下，升力、阻力以及俯仰力矩数值随着风速增加单调增加，总升阻比单调减小，当风速增大至1 m/s时，升力、阻力以及俯仰力矩数值等变化可忽略不计，但当风速增大到8 m/s时，总升力增加约16.2 N，总阻力增加约25 N，俯仰力矩数值增加约17.1 Nm，滑雪板升力增加约9.85 N，滑雪板阻力增加约15 N，滑雪板俯仰力矩数值增加约22.5 Nm；在竖直向下风情况下，升力、阻力以及俯仰力矩数值随着风速增加单调减小，总升阻比单调增加，当风速增大至1 m/s时，升力、阻力以及俯仰力矩数值等变化可忽略不计，但当风速增大到8 m/s时，总升力减小约19.7 N，总阻力减小约31 N，俯仰力矩数值减小约20.6 Nm，滑雪板升力减小约11.6 N，滑雪板阻力减小约18 N，滑雪板俯仰力矩数值减小约27.3 Nm。

侧向不同环境风下多体系统的力学特性随风速变化曲线如图7所示。可以看出，受侧向环境风的影响，运动员/滑雪板多体系统明显产生偏航力、偏航力矩、翻滚力矩，这些力和力矩数值随着风速增加变化趋势一致，均呈现抛物线式凸曲线形式单调增大的关系。当风速增大至1.5 m/s时，偏航力、偏航力矩以及翻滚力矩数值很小，可忽略不计，但当风速增大到7.5 m/s时，偏航力约为26.3 N，偏航力矩约为6.32 Nm，翻滚力矩数值约7.8 Nm。同时，侧向环境风也会对运动员/滑雪板多体系统、运动员的升力、阻力以及俯仰力矩产生一定的影响，同样这些力和力矩数值随着风速增加变化趋势一致，均呈现抛物线式凸曲线形式单调增大的关系。当风速增大至1.5 m/s时，升力、阻力以及俯仰力矩数值等变化可忽略不计，但当风速增大到7.5 m/s时，总升力增加约13.7 N，总阻力增加约12.3 N，俯仰力矩数值增加约3.25 Nm。

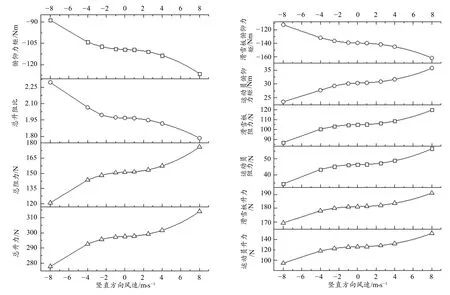
图6 竖直上/下风工况下力学特性随风速变化曲线Figure 6.Variation of Mechanical Characteristics with Wind Speed under Vertical Upper/down Wind Conditions

2.2 流场形态

不同环境风下涡流形态和气流速度流线如图8～10所示。运动员身后以及滑雪板后面的涡流形态均主要以回流涡结构形式出现，此结构会加速能量耗散。同时，气流速度在运动员以及滑雪板上均发生了流动分离。运动员身后主要产生2对涡结构；滑雪板后侧主要有6对涡结构产生。从图8中可以看出，随着水平方向风速的变化，涡流形态变化不明显，但其流线速度值变化非常明显。从图9中可以看出，随着竖直方向风速的变化，涡流形态以及流线速度值变化均不太明显。从图10中可以看出，随着侧向风速的增大，滑雪板后涡结构尺度相对变化较小，但运动员后侧的涡流变化明显，向侧向风方向偏移越来越大。

3 讨论

3.1 研究结果及风况的普适性

Müller等（1996）以及Schmolzer等（2005）统计分析了世界一流水平跳台滑雪运动员在飞行稳定阶段各姿态参数的实际测量结果，并给出了这些姿态参数通常的变化范围，即迎风角φ在25°～40°范围内变化，滑雪板与速度方向夹角α在25°～40°范围内变化，滑雪板与身体夹角θ在 10°～20°范围内变化，上半身弯曲角度 β 在 10°～25°范围内变化，滑雪板夹角λ在20°～40°范围内变化，速度V在25 m/s～32 m/s范围内变化。同时，根据胡齐等（2018a）研究成果，建议优选的滑雪板夹角λ范围为24°～32°。本研究迎风角φ、滑雪板与速度方向夹角α、滑雪板与身体夹角θ、上半身弯曲角度β，滑雪板夹角λ、速度V等姿态参数的取值均在上述范围内，研究结果具有较好的普适性。

水平方向环境风是自然环境中的常见风况，但是只有垂直方向或只有侧向的环境风实际中并不常见。而与飞行方向成一定夹角的环境风比较常见，但此风况种类太多。通过对3个方向正交的环境风进行耦合叠加，可以获得很多种类的与飞行方向成一定夹角的风况，其对应的结果也可进行耦合叠加。因此，分别研究水平方向环境风、竖直方向环境风与侧向环境风可能更具有普适性。

3.2 水平方向环境风对空中飞行气动特性的影响

本研究结果显示，水平方向环境风对运动员/滑雪板多体系统的升力、阻力以及俯仰力矩产生影响很大，当然这些力学特性结果数值也可能因多体系统空中飞行姿态 的不同而不同，尤其是运动员姿态。

图7 侧向风工况下力学特性随风速变化曲线Figure 7.Variation of Mechanical Characteristics with Wind Speed under Lateral Wind Conditions

图8 水平顺/逆风工况下流场形态Figure 8.Flow Field Form under Horizontal Down/head Wind Conditions

图9 竖直上/下风工况下流场形态Figure 9.Flow Field Form under Vertical Upper/down Wind Conditions

图10 侧向风工况下流场形态Figure 10.Flow Field Form under Lateral Wind Conditions

不难发现，不管是水平顺风还是水平逆风，升力、阻力以及俯仰力矩变化明显，对空中飞行气动特性的影响很大，非常不利于运动员空中飞行姿态稳定控制，尤其是俯仰姿态控制，同时会对飞行跳跃距离产生较大的影响（Jung et al.，2019；Müller et al.，1996；Seo et al.，2004；Virmavirta et al.，2012）。值得注意的是，水平逆风主要产生类似飞行爬升的效果，而水平顺风主要产生类似飞行失速的效果，同时水平逆风情况下多体系统力学特性数值结果的增长速度（变化斜率）大于水平顺风情况下多体系统力学特性数值结果的减小速度（变化斜率的绝对值）。

另一个值得注意的现象是，不仅滑雪板升力以及阻力分别占据总升力以及总阻力的60%以上，而且滑雪板俯仰力矩值是多体系统俯仰力矩值的1.15倍以上，在多体系统俯仰力矩中始终占据主导地位。因此，滑雪板气动特性在运动员/滑雪板多体系统中起着重要作用，不仅要关注运动员身体姿态，而且也要关注滑雪板姿态（胡齐等，2018a）。

另外，从流场形态结果看出，随着水平方向环境风速度变化，涡流形态变化不明显，但其流线速度值变化非常明显，说明在水平方向环境风影响下多体系统的力学特性变化明显，与之前获取的力学特性数值统计结果变化趋势相符。

3.3 竖直方向环境风对空中飞行气动特性的影响

本研究结果显示，竖直方向环境风对多体系统的升力、阻力以及俯仰力矩产生影响。在相同的风速下，与水平方向环境风相比，竖直方向环境风对多体系统气动特性的影响小很多。同时，这些力学特性结果数值也可能因多体系统空中飞行姿态的不同而不同，尤其是运动员姿态。

不难发现，在风速较小时（小于2.5 m/s），升力、阻力以及俯仰力矩增加缓慢，在风速较大时（大于4 m/s），升力、阻力以及俯仰力矩开始相对快速增加，对空中飞行气动特性的影响变大，并对运动员飞行稳定控制产生一定的影响。进一步发现，竖直向上环境风使得升力、阻力、俯仰力矩增大，竖直向下风使得升力、阻力以及俯仰力矩减小，而且增长幅度以及减少幅度均与风速的平方成近似线性关系，但值得注意的是，竖直向上环境风情况下的增长幅度明显小于竖直向下风情况下的减少幅度。总升阻比的变化情况与上述情况恰恰相反。

另一个值得注意的现象是，竖直向上环境风产生的升力造成多体系统阻力增加，竖直向上环境风产生的阻力造成多体系统升力增加；竖直向下环境风产生的升力造成多体系统阻力减小，竖直向下环境风产生的阻力造成多体系统升力减小。另外，从流场形态结果看出，随着竖直方向环境风速度变化，涡流形态以及流线速度值变化均不明显，说明竖直方向环境风对多体系统气动特性的影响较小，与之前获取的力学特性数值统计结果相符。

3.4 侧向环境风对空中飞行气动特性的影响

本研究结果显示，侧向环境风对多体系统的升力、阻力以及俯仰力矩产生影响。在相同的风速下，与竖直方向环境风相比，侧向环境风对多体系统气动特性的影响略小一些，但影响情况复杂得多，这是因为受侧向环境风影响，多体系统会明显产生偏航力、偏航力矩、翻滚力矩。同时，这些力学特性结果数值也可能因多体系统空中飞行姿态的不同而不同，尤其是运动员姿态。

首先，在风速较小时（小于3 m/s），偏航力、偏航力矩、翻滚力矩增加缓慢，在风速较大时（大于4.5 m/s），偏航力、偏航力矩、翻滚力矩快速增加，非常不利于空中飞行稳定控制；进一步发现，偏航力、偏航力矩、翻滚力矩与风速的平方成近似线性关系。值得注意的是，运动员产生的偏航力、偏航力矩、翻滚力矩始终占据绝对主导地位，滑雪板的影响较小，应重点关注侧向环境风下运动员姿态对空中飞行气动特性及稳定性的影响。

其次，在风速较小时（小于3 m/s），升力、阻力以及俯仰力矩增加缓慢，在风速较大时（大于4.5 m/s），升力、阻力以及俯仰力矩开始快速增加，这对运动员空中飞行稳定控制提出了更高的要求。一个值得注意的现象是，总升力、总阻力、俯仰力矩的增长幅度与运动员的升力、阻力以及俯仰力矩的增长幅度几乎一样，这也说明，由于运动员身体形态类似飞机机翼外形，在侧向环境风下不仅产生阻力效果（也就是上述的偏航力），而且产生升力效果，从而使得运动员升力、阻力以及俯仰力矩发生变化，进而导致整个多体系统的总升力、总阻力、俯仰力矩的变化。但是，滑雪板对应的力学特性几乎不产生任何变化。

另外，从流场形态结果看出，随着侧向风速的增大，滑雪板后涡结构尺度相对变化较小，但运动员后侧的涡流变化明显，向侧向风方向偏移越来越大，说明运动员受侧向风的影响较大，其产生的力和力矩变化更为明显。这也与之前获取的力学特性数值统计结果相符。

4 结论

1）水平方向环境风对跳台滑雪空中飞行气动特性的影响非常明显，相较而言，竖直方向环境风和侧向环境风对空中飞行气动特性的影响小很多，但侧向环境风的影响情况较为复杂，对运动员/滑雪板多体系统产生较为明显的偏航力、偏航力矩、翻滚力矩。这些影响机理可通过风洞实验进一步探究验证。

2）不管是水平顺风还是水平逆风，升力、阻力以及俯仰力矩变化明显，与风速呈现近似线性关系，对空中飞行气动特性的影响很大，同时水平逆风情况下力学特性数值结果的增长速度（变化斜率）大于水平顺风情况下力学特性数值结果的减小速度（变化斜率的绝对值）。

3）在竖直方向风速较小时（小于2.5 m/s），升力、阻力以及俯仰力矩增加缓慢，在竖直方向风速较大时（大于4 m/s），升力、阻力以及俯仰力矩开始相对快速增加，对空中飞行气动特性的影响变大，并对运动员飞行稳定控制产生一定的影响。同时，竖直向上环境风使得升力、阻力、俯仰力矩增大，竖直向下环境风使得升力、阻力以及俯仰力矩减小，而且竖直向上环境风情况下增长幅度明显小于竖直向下环境风情况下减少幅度。

4）侧向环境风产生偏航力、偏航力矩、翻滚力矩，在风速较小（小于3 m/s）时，这些力和力矩很小，在风速较大（大于4.5 m/s）时，比较明显且不可忽略，但运动员产生的偏航力、偏航力矩、翻滚力矩占据主导地位，滑雪板的影响很小。同时，侧向环境风对运动员的升力、阻力以及俯仰力矩产生影响。在风速较小（小于3 m/s）时，影响很小，在风速较大（大于4.5 m/s）时，影响比较明显且不可忽略，但对滑雪板几乎不产生任何影响。

5）环境风对跳台滑雪空中飞行气动特性的影响机理能够为比赛临场预判与决策提供有效的辅助支持，也为运动员空中飞行稳定性控制与技术训练提供科学指导。