Scrratch计算质数
2020-06-30
在数学王国中,数学家根据不同数的特性给它们起了不同的名字,有的叫奇数,有的叫偶数,还有的叫质数……今天我们就来探讨一下这个质数。
质数又称素数,一个大于1的自然数,除了1和它自身外不能被其他自然数整除的数叫做质数,否则称为合数。质数的个数是无穷多的,2、3、5、7、11这些都是质数。懂得什么是质数后,我们就会考虑如何做一个程序判断该数是不是质数呢?虽然质数是无穷多个,我们能不能计算出100以内的所有质数呢?

已知,质数就是只能被1和它自身两个数相除的数。因此,要判断一个大于2的自然数n是不是质数(默认2是为质数),最简单的办法就是看n能不能被2到n-1中的某个数整除。只要有一个数能被n整除,n就是合数;如果都不能整除,n就是质数。比如97,我们就看它能不能被2到96中的某一个数整除。很显然97不能被2到96中的数字给整除,所以97是一个质数。
这个方法虽然简单粗暴,却也有很大弱点,就是随着数字变大会消耗很长的运算时间。如果数字非常巨大还用手工计算当然是不可能,而使用计算机来计算却还是有那么一点希望的,计算质数也是测试计算机运算能力的一个常用办法呢。
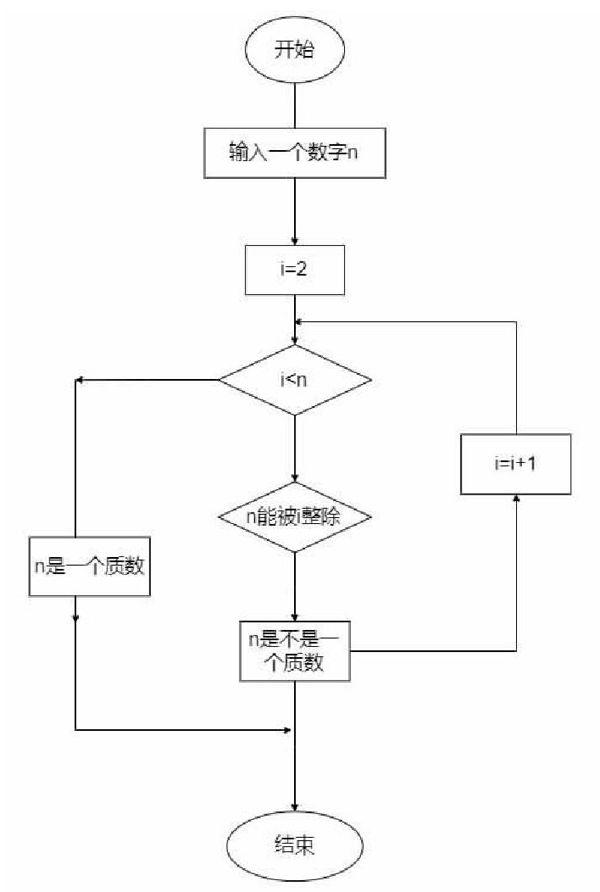
好了现在我们先来看看判断某一个数字是不是质数的流程图。
判断输入的数字是否能被i给整除,如果该数字能被i整除了(余数=0),那么該数就不是质数,是合数,如果不能,则该数字就是质数。
在此基础上我们从2开始依次判断每个数是不是质数,如果是的话就加入到质数列表里,否则加入合数列表。还有几个技巧就是当出现整除情况后,怎样停止本次循环,我们使用直接赋值n=1完成循环判断。然后去判断下一个自然数是不是质数。
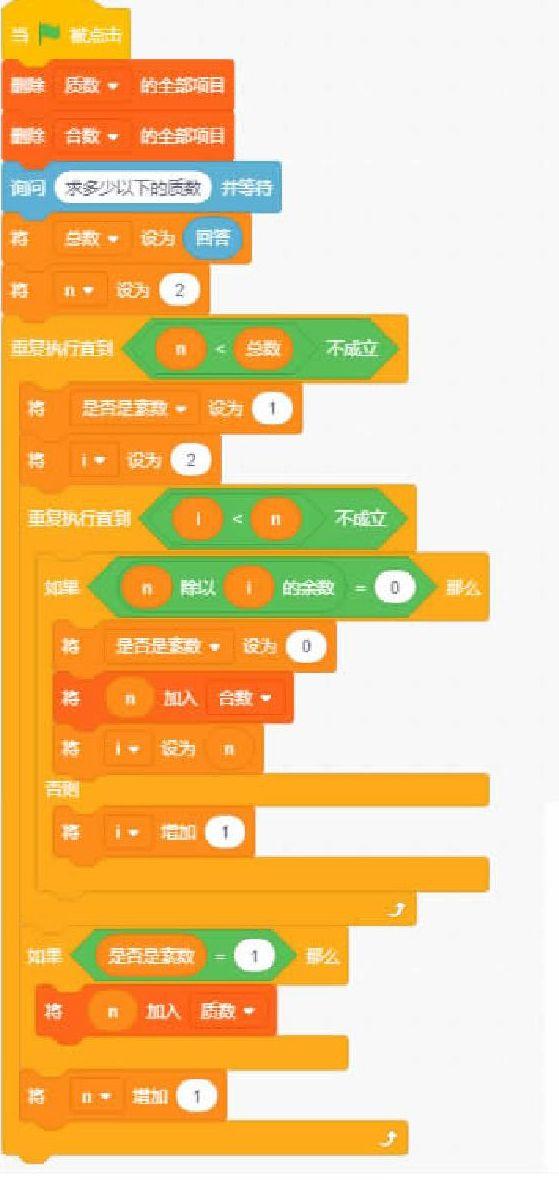
结合流程图和程序代码,我们一起来读懂代码。
总数是用户设定的计算范围。
变量n是总数以内的自然数从2开始,依次递增。
变量i作为除数,取值范围2到n。
变量“是否为质数”用于记录判断n是否质数的结果。初始默认这个数是素数标记为1,如果能被整除那么就改变值为0,即不是质数,停止本次重复执行。
梅森素数
提前停止本次重复是一个减少计算量的小技巧。因为需要重复执行到i=n,一旦遇到可以整除时就直接修改i的值,使执行结束的条件成立,减少不必要的运算量。
每个自然数n重复执行除法判断结束后根据变量“是否为质数”来确定最终结果,如果等于1就是质数,添加进质数列表,否则加入合数列表。
小知识:梅森素数
与质数(素数)有关的“互联网梅森素数大搜索(GIMPS)”项目是旨在找到更大的梅森素数——既是梅森数(少量素数可写成“2的n次方减1”<2^n-1>的形式)又是素数(质数)的数。
手工运算发现的最大梅森素数是1876年数学家卢卡斯发现的2^127-1.这是一个39位的数。2018年,计算机发现了第51个梅森素数:2^82589933-1(被称为M82589933),共有24862048位。