何时算？何时不算？

陈石单

摘 要：数图形是学生经历把生活中的现实问题抽象成数图形的数学问题，并利用画图策略解决问题的过程，在数图形的过程中，能够逐步形成有序思考的良好习惯，做到不重复，不遗漏，在学生独立思考和自主探究，发现规律，有条理地表达过程中发展有序思考能力。

关键词：小学数学 练习题 理清问题

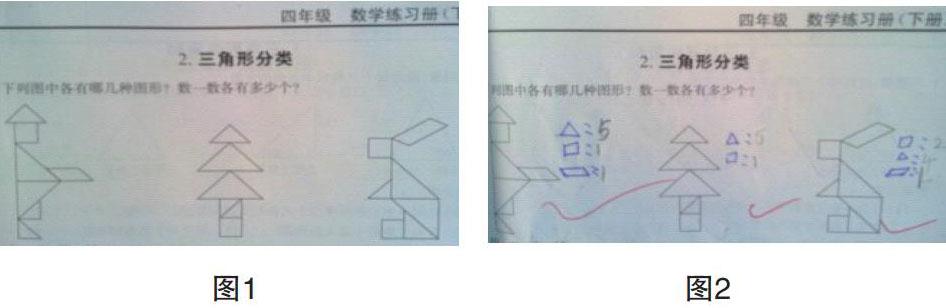
学习了三角形的分类以后，学生做了省编练习册上一道习题（如图1），作业评讲时，我指名一个学生说第一个图里面有几种图形，各有多少个？学生很快答出了如图2的答案。但马上遭到了一些同学的反击。“不是5个三角形，是6个三角形。”

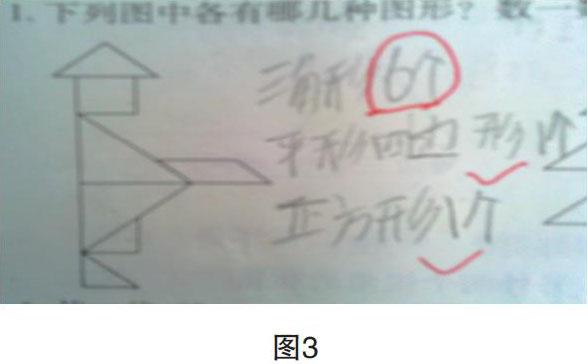
其中一向善于思考的黄小豪同学站起来说：“老师，这个钓鱼人身体部分的两个三角形还可以拼成一个大三角形，因此，应该有6个三角形（如图3）才对。”学生说得很在理，这两个三角形是可以拼成一个新的三角形啊，但又感觉有些不对劲。

于是，我又把题目要求细读了一遍，“下列图中各有几种图形？”这是要求我们干什么呢？这一读一问，我有了茅塞顿开的感觉，这是要求我们将本图的几种图形分类。想到了这些天讲到的分类：分类是要有标准的，在这个标准下分类的原则就是不重复、不遗漏。学生可能对分类的原则理解还不够。

想到这里，我向学生提问：“钓鱼人这幅图一共有多少个图形？”

学生不假思索就说出：“ 7个。”

师：有几种图形，是要求我们干什么呢？

生：“要求我们把这些图形分类。”

师：分类要注意什么？

生：不重复、不遗漏。

师：这个图可以分几种图形呢？

生： 3种。

师：哪3种？

生：三角形、長方形、平行四边形。

师：长方形、平行四边形各有多少个？

生：长方形1个，平行四边形1个。

师：三角形算6个，总个数就有8个，重复了，因而只能算5个。

这时黄小豪马上站起来，举起草稿本，他在上面画了一个图（如图4），说：这个图中，为什么又要算3个三角形呢？究竟什么时候算2个，什么时候算3个呢？

没想到学生会有这么一连串的问题，令我有些措手不及。

我稍微镇定了一下，问道：这道题又是要我们干什么呢？

黄：数一数，这个图中一共有几个三角形？

师：这道题需要我们对这几个图形分类了吗？

黄：不需要我们分类。

师：不需要分类，就不考虑是否重复了，只要不遗漏就行。我们就应该把所有的三角形（包括拼起来的）都算进去。

黄：哦，我明白您的意思了，您是说，如果题目要求分类，就要做到不重复，不遗漏;如果题目没要求分类，我们就应该所有的同类都算进去。

师：你听得很仔细，我说的是这个意思。

由处理此题的情境，我想到了老师们经常纠结的两类题目。

1、在认识了正方形是特殊的长方形之后有这样一类题目：

在上面图形中，长方形有（）个，正方形有（）个，圆有（）个，三角形有（）个。

2、长方体的六个面一定都是长方形，这个命题是否正确？

第一类题目正方形的个数到底应不应该算在长方形之列？

这题是要把图形按形状分类，根据不重复、不遗漏的分类原则，图形的总数不能增加，因而正方形不应算在长方形之列，应该单独算。

第二类题目争论的关键就是有两个面是正方形的特殊长方形，正方形的两个面是算长方形，还是算成单独的正方形？

这题从分类的角度看，是按是否为长方形做标准来对六个面进行分类，六个面都符合这个标准就是长方体，如果有一个面不是长方形，就不是长方体了。在这个标准下，六个面既没有重复，又没有遗漏，就没有必要再往下细分了。因此，这一题正方形应该算在长方形之列，不单独算。

总的说来，图形中的这类问题，如果不能确定何时算，何时不算？不妨从分类角度来考虑，这将有助于我们把这类问题理清。