当“翻折”邂逅“多解”

孙春红

(江苏省南京市金陵中学溧水分校 211200)

本文以苏科版七年级下册第42页第七章复习题第19题为例，探索一题多解，可以提高学生的举一反三能力，激发学生寻找最优解的动力，可以更好地提升学生数学素养，有利于提高学生的发散思维和创新精神.

题目如图，将△ABC纸片沿DE折叠，使点A落在四边形BCDE内点A′的位置.探索∠A与∠1+∠2之间的数量关系，并说明理由.

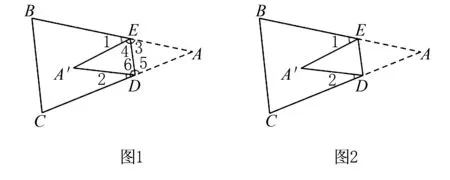
方法一：用三角形的内角和定理和邻补角的知识

分析如图2，因为三角形纸片ABC沿DE折叠，所以△ADE≅△A′DE，∠3=∠4，∠5=∠6.要求∠A与∠1+∠2之间的数量关系，可以从问题出发，思考∠A如何表示，∠1，∠2如何表示.在△ADE中∠A=180°-(∠3+∠5)，∠1=180°-(∠3+∠4)，∠2=180°-(∠5+∠6).

解因为三角形纸片ABC沿DE折叠，所以△ADE≅△A′DE，∠3=∠4，∠5=∠6.

设∠3=∠4=x， ∠5=∠6=y，因为在△ADE中∠A=180°-(∠3+∠5)，所以 ∠A=180°-(x +y).

因为∠AEA′与∠1互补，所以∠1=180°-∠AEA′=180°-(∠3+∠4)=180°-2x.

因为∠ADA′与∠2互补，所以∠2=180°-∠ADA′=180°-(∠5+∠6)=180°-2y，即∠1+∠2=360°-2(x +y).所以∠1+∠2=2∠A.

方法二：用三角形的外角解决问题

分析如图2，因为三角形纸片ABC沿DE折叠，所以△ADE≅△A′DE，∠3=∠4，∠5=∠6.因为∠BED和∠CDE分别为△ADE的外角，而且∠BED既可以用∠A和∠5表示，又可以用∠1和∠4表示；同理∠CDE可以用∠A和∠3表示，也可以用∠2和∠6表示.根据等式的性质可以表示出∠A与∠1+∠2之间的数量关系.

解因为三角形纸片ABC沿DE折叠，所以△ADE≅△A′DE，∠3=∠4，∠5=∠6.

因为∠BED和∠CDE分别为△ADE的外角，所以∠BED=∠A+∠5，∠CDE=∠A+∠3.

又因为∠BED=∠1+∠4，∠CDE=∠2+∠6，所以∠A+∠5=∠1+∠4 ①，∠A+∠3=∠2+∠6 ②.

①+②得2∠A+∠5+∠3=∠1+∠4+∠2+∠6，即2∠A=∠1+∠2.

方法三：用平角和三角形的内角和定理

分析如图2，因为三角形纸片ABC沿DE折叠，所以△ADE≅△A′DE，∠3=∠4，∠5=∠6.由∠AEB=180°可知∠1+∠3+∠4=180°，由△A′DE的内角和为180°，可知∠A′+∠4+∠6=180°，再根据等式的性质，可以表示出∠A与∠1+∠2之间的数量关系.

解因为三角形纸片ABC沿DE折叠，所以△ADE≅△A′DE，∠A=∠A′，∠3=∠4，∠5=∠6.

因为∠AEB=180°，△A′DE的内角和为180°，所以∠1+∠3+∠4=180°，∠A′+∠4+∠6=180°， 所以∠1+∠3=∠A+∠6. ①

同理 ∠2+∠5=∠A+∠4. ②

①+②得∠1+∠2=2∠A.

方法四：三角形内角和定理和平角的知识

分析如图2，因为三角形纸片ABC沿DE折叠，所以△ADE≅△A′DE，∠3=∠4，∠5=∠6.由于△ADE的内角和为180°，∠A可以用180°-(∠3+∠5)表示，而∠3可以用∠1的代数式表示，∠5可以用∠2的代数式表示，再经过化简可以表示出∠A与∠1+∠2之间的数量关系.

解因为三角形纸片ABC沿DE折叠，所以△ADE≅△A′DE，∠A=∠A′，∠3=∠4，∠5=∠6.

方法五：运用四边形的内角和和三角形的内角解决问题

分析如图2，因为三角形纸片ABC沿DE折叠，所以△ADE≅△A′DE，∠1+∠2也在四边形BCDE中，由四边形BCDE的内角和为360°，可以表示出∠1+∠2，而其中∠4+∠6和∠B+∠C又可以分别用∠A表示，再经过化简可以表示出∠A与∠1+∠2之间的数量关系.

解因为三角形纸片ABC沿DE折叠，所以△ADE≅△A′DE，∠A=∠A′，∠3=∠4，∠5=∠6.因为四边形BCDE的内角和为360°，所以∠1+∠2=360°-(∠4+∠6+∠B+∠C).因为△ADE和△A′DE的内角和为180°，所以∠4+∠6=180°-∠A′，∠B+∠C=180°-∠A，所以∠1+∠2=2∠A.