孔洞型碳酸盐岩储集层中洞对电阻率的影响
2020-06-30何家欢李闽周克明杨雨谢冰李农党录瑞唐雁冰
何家欢,李闽,周克明,杨雨,谢冰,李农,党录瑞,唐雁冰
(1.西南石油大学油气藏地质及开发工程国家重点实验室,成都610500;2.中国石油西南油气田勘探开发研究院,成都610213;3.中国石油集团公司碳酸盐岩储集层重点实验室,杭州310023;4.中国石油西南油气田公司,成都610051)
0 引言
碳酸盐岩油气藏储量丰富,世界范围内储量规模和产量大的油气藏多为碳酸盐岩油气藏[1-6]。中国碳酸盐岩油气藏主要分布在四川、塔里木和鄂尔多斯等盆地。塔里木盆地碳酸盐岩储集层以岩溶缝洞型为主要特征。鄂尔多斯盆地碳酸盐岩储集层以岩溶孔洞型为主要特征。四川盆地震旦系灯影组、下寒武统龙王庙组、泥盆系观雾山组、石炭系黄龙组、二叠系栖霞组、三叠系飞仙关组和嘉陵江组以及雷口坡组等均发育溶洞型白云岩储集层,而灰岩岩溶缝洞储集层主要发育在中二叠统茅口组。此外,四川盆地的震旦系、寒武系和中二叠统均有孔洞型储集层发育。研究表明,四川盆地海相碳酸盐岩天然气资源量占常规天然气资源量的85%,已成为四川盆地天然气生产的主力层系[7-9]。
溶洞发育的碳酸盐岩储集层导电机理十分复杂,利用阿尔奇(Archie)公式建立储集层电阻率与含水饱和度之间的关系比较困难。Archie公式是1942年针对碎屑岩提出的[10],该公式须满足 3个条件:①岩石孔隙度在空间上的分布是均匀的;②岩石所含流体饱和度在空间上分布也是均匀的;③岩石的电学性质各向同性。显然,孔洞型碳酸盐岩储集层并不满足上述 3个条件,洞的发育必然使储集层电阻率异常,直接用Archie公式来描述孔洞型储集层电阻率与含水饱和度的关系比较困难。目前国际上探测溶洞的重要技术手段是利用充水溶洞电阻率异常特征来探查隐伏溶洞[11-20]。
在测井尺度及岩心尺度方面,洞的发育给测井解释人员认识储集层导电机理和确定油气饱和度带来巨大困难。国内外针对孔洞型碳酸盐岩的电阻率虽有研究[21-24],但结合孔洞型储集层岩石的孔隙结构特征构建网络模型定量研究储集层电阻率的研究很少。刘向君等[25]和熊健等[26]通过岩心电阻率实验,结合孔隙度和渗透率及阿尔奇公式中的参数进行分析研究,但未考虑岩石的孔隙结构特征。张兆辉等[27]利用电阻串并联导电原理,尝试理论模拟孔洞型储集层电阻率,得到电阻率随喉道直径增加而快速下降、随基质和地层水电阻率增加而增大的认识,但模拟所采用的模型较简单,不能反映孔洞型储集层中孔径分布和孔洞比等孔隙结构特征对储集层电阻率的影响。针对上述不足,本文通过提取孔洞型碳酸盐岩储集层孔隙结构特征参数,利用逾渗网络模拟技术计算基质电阻率,建立分段式跨尺度电阻率计算方法,得到洞孔隙度和洞含水饱和度与储集层电阻率的关系。
1 孔洞型储集层电阻率数值模拟技术
根据孔隙结构特征和逾渗网络模拟技术模拟储集层岩石电阻率的基本思路是利用网络模型来描述复杂的微观孔隙结构,利用逾渗理论描述孔隙空间的宏观输运性质与微观结构之间的定量关系。其优势在于能够在模拟中体现储集层岩石孔径分布和配位数等孔隙结构特征,尽可能地还原真实岩心孔隙结构。
1.1 孔洞型储集层岩石孔隙结构特征参数提取
以四川盆地安岳气田高石梯—磨溪区块 G101井震旦系灯影组白云岩样品为例,孔洞型储集层岩石孔隙结构特征参数提取分为以下几个步骤:①通过CT扫描提取复杂储集层岩石孔隙结构特征参数(见图1a);②通过VG Studio Max 3.0.1 64bit软件导入岩心扫描图像得到岩心孔隙度和孔隙空间分布规律(见图1b)及孔径分布频率(见图1c);③利用Simple Core软件对储集层岩石进行配位数统计(平均配位数为 2.867),生成球棍模型(见图1d)。
Jerauld等[28]研究发现,当具有一定结构的规则网络与无序网络的连通性相同时,两种网络的宏观流动和传导性质也相同。因此只需建立一种同时满足岩心孔隙度、孔径分布频率和配位数的网络模型,就可模拟储集层电阻率。王克文等[29]通过建立三维立方体逾渗网络模型研究了流体和电流的输运特性,并与真实岩心实验数据进行了对比,证实了逾渗网络模型能够与真实岩心的微观特征和宏观输运性质相似。Bernabé等[30-31]采用二维逾渗网络模型以及三维逾渗网络模型研究了单孔介质的渗透率和电导率。单孔介质逾渗网络模型是在建立二维或三维等间距网格的基础上,通过逾渗概率耦合平均配位数和满足喉道半径分布规律建立的网络模型。
在孔径分布变异系数不大的情况下,“等间距”的假设条件是可以接受的。但由图1c可知,该样品最小孔径为0.02 mm,最大孔径为10 mm,二者尺度相差500倍,这样的尺度差异不再满足“等间距”假设条件。同时,与最大孔径相连的喉道数量将比最小孔径多出数量级的差异,利用平均配位数生成与该孔(洞)连接的喉道数已不再合理。因此,模拟典型孔洞型储集层特征的岩石电阻率,必须建立新的电阻率模拟方法。
1.2 分段跨尺度电阻率计算方法
针对孔洞型岩石,前人提出了嵌入式逾渗网络模型、等效双重介质逾渗网络模型两种思路。嵌入式逾渗网络模型由Békri等[32-33]提出,通过将小尺度孔喉网络模型叠加到大尺度孔隙网络模型上建立逾渗网络模型。但由于小尺度网络模型的嵌入使得该类双重介质网络模型中节点数量巨大,模拟计算耗时,限制了相关研究和推广应用。等效双重介质网络模型由Ahmadi[34]提出,将模型中的基质和孔喉进行拆分后再分别进行并联,更好地反映了较大溶孔的电阻率性质。
为有效表征洞对电阻率的影响,又要充分发挥逾渗网络在表征单孔介质时的优势,本文把孔径分布频率分为两部分处理。如图1c所示,把红线左侧孔径小于1 mm的部分作为“基本单元”,基本单元电阻率按Li等[35]提出的LBT方法计算;把红线右侧孔径大于1 mm的部分,利用随机算法产生符合实际孔径分布的网格模型(见图2a)。用基本网格来表征洞,比如孔径为10 mm的洞等同于10个“基本单元”。把孔径小于0.1 mm的部分作为“基本单元”所产生的网格模型如图2b所示。显然,当储集层含水饱和度为100%时,基本单元的电阻率可由LBT方法计算,而洞的电阻率则等于地层水电阻率。
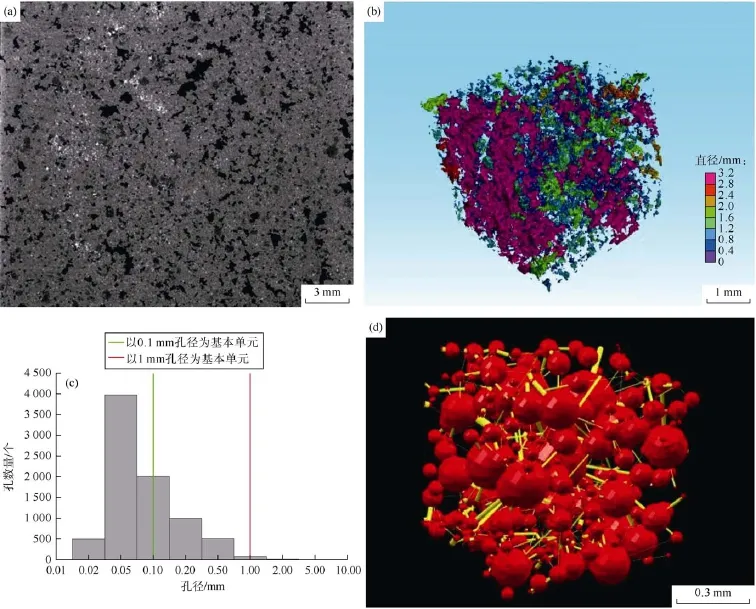
图1 孔洞型储集层岩石孔隙结构特征参数提取
依据电流守恒定律计算岩石电阻率,多孔介质中的电位分布用以下方程组表示:

在二维直角坐标系中,电流密度为:

电流密度的散度为:
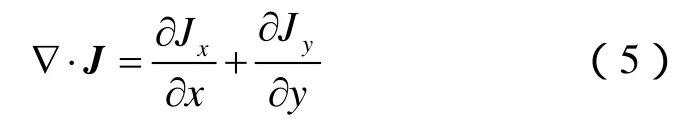
电场强度为:

二维向量微分算子为:

(1)式的物理意义是电流密度的散度等于一个单位体积里流出的电荷量,即该点处的电荷密度。(2)式表示电流密度等于电场强度与电导率的乘积,与位移电流密度的和。对于静止参照系,位移电流密度Je为0。(3)式表示电场强度等于电势差的负梯度。
按照孔径分布规律产生各种大小的溶洞,通过有限元模拟方法,求取孔洞型储集层岩石的电势分布(见图3)。图4展示了以0.07 m为边长的正方形中的电势场分布,研究对象顶端给予恒定电势1 V,底端接地为0 V,图中方框代表不同孔径的洞,洞中饱和地层水,其余位置代表基质,利用(8)式和(9)式计算边界上的电流密度。
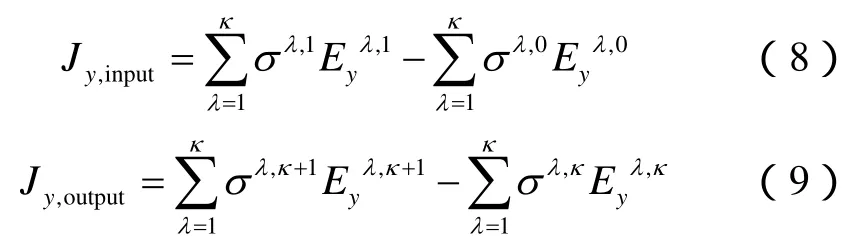
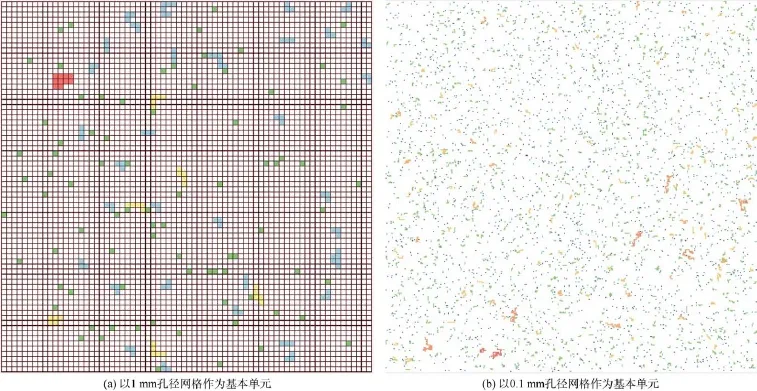
图2 不同孔径分布规律产生的随机网格模型(图中不同颜色代表不同大小洞(孔),白色代表基质)

图3 有限元求解网格模型示意图
若Jy,input与Jy,output相等,则表明孔洞型储集层电势分布已达到稳定。利用(10)式即可求得孔洞型储集层的电阻率值。

根据分段式跨尺度电阻率计算方法,可得到洞孔隙度与电阻率以及洞含水饱和度、孔洞比与电阻率的关系。
2 洞孔隙度与电阻率的关系
2.1 基本概念
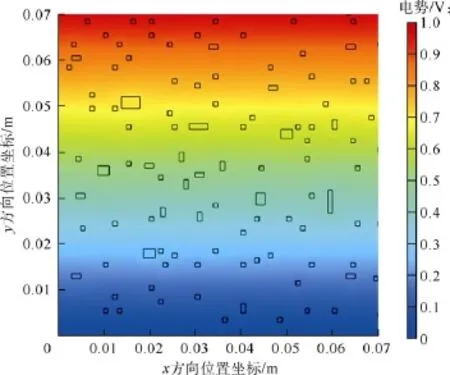
图4 孔洞型储集层电势分布模拟结果(图中方框代表不同孔径的洞,其余位置代表基质)
将所研究的区域定义为“研究对象”,其大小或规模取决于研究人员。如图 5所示,当研究人员研究直径2.5 cm的柱塞样岩心时,研究对象的就是蓝色圆圈部分;当研究人员研究全直径岩心时,研究对象就是黄色方框部分;如果研究人员研究电测井资料,研究对象的直径就是电测井探头在井筒周围的探测直径;如果研究人员研究整个地层,研究对象就是整个地层。定义“洞孔隙度”φc为洞体积与研究对象体积之比。为了简化计算并更好地以图示方式展示成果,本文用平面代替了体积。规定N值满足以下条件:N2个基本单元的体积等于研究对象的总体积,φc和N值均与研究对象的选取有关。对于 1个同样尺寸大小的洞,由于研究对象不同,其N值也不同,所代表的洞孔隙度的意义也不同。

图5 研究对象选取示意图
2.2 洞孔隙度的阈值
数值模拟时假设基质电阻率为500 Ω·m、溶洞中地层水的电阻率为0.120 6 Ω·m。N值分别取3,5,7,10来模拟研究对象电阻率的变化规律,随着洞孔隙度的增加,孔洞型岩心电阻率不断下降,当洞孔隙度增加到一定程度时,研究对象电阻率将快速下降到与地层水电阻率相同的数量级(见图6)。将电阻率发生“突降”时的洞孔隙度称为洞孔隙度阈值(φcc)。
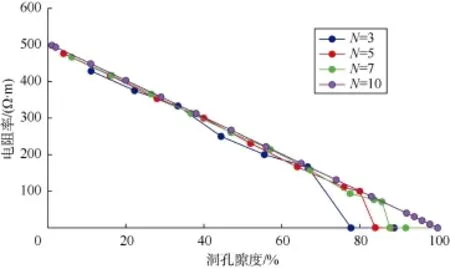
图6 研究对象电阻率与洞孔隙度的关系
根据数值模拟统计发现,洞孔隙度阈值与研究单位基本单元个数的平方根N值存在如下关系:

N值越大,意味着单个最小洞体积占研究对象总体积的比例越小,φcc值就会越大,研究对象电阻率就越难到达地层水电阻率的水平。在洞孔隙度到达阈值之前,研究对象电阻率与洞孔隙度满足以下关系:

(12)式的物理意义是,当岩心100%饱和盐水时,研究对象电阻率的大小等于基质电阻率与基质在研究对象中体积占比的乘积。(12)式存在两种极端情况:①当洞与研究对象的体积比值为无穷小时,洞孔隙度为0,洞孔隙度阈值无限接近100%,Ros与Rom相等,岩电特征完全符合Archie公式,(12)式退化为Archie公式;②当洞孔隙度大于洞孔隙度阈值时,Ros与Rw相近,研究对象的电阻率近似等于地层水电阻率。
3 洞含水饱和度与电阻率的关系
相对于洞孔隙度与电阻率的关系,研究人员更加关注含水饱和度与电阻率的关系[36-38]。研究表明,对于孔洞型储集层,建立电阻率与含水饱和度的相关关系很困难,但把洞与基质的电阻率分开研究,发现洞含水饱和度对研究对象的电阻率影响较小。
3.1 洞含水饱和度对电阻率的影响
假设样品孔隙度为 5%,其中洞孔隙度为 2.5%,基质孔隙度为2.5%,研究对象中含水饱和度的减少先从洞开始。当洞含水饱和度减少到接近于 0时,基质孔隙中的含水饱和度才逐渐减少。模拟结果显示研究对象在洞含水饱和度减少到 0之前,研究对象的电阻率变化并不明显(见图7)。
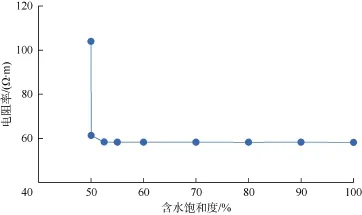
图7 电阻率与含水饱和度模拟曲线
岩电实验也得到类似结论。以四川盆地安岳气田磨溪区块M203井寒武系龙王庙组135号样品为例(见图8a),样品孔隙度为11.41%,采用矿化度为50 g/L的盐水进行抽真空加压饱和,盐水电阻率为0.14 Ω·m。按照现行行业标准[39]进行岩电实验,实验结果表明,当岩心表面上的洞充满盐水时,岩石电阻值为 0.984 kΩ,当岩心表面上的洞没有盐水时,岩石电阻值为0.997 kΩ。由此可知,洞所占空间的含水饱和度下降对电阻率的贡献较小。发育洞的样品电阻率曲线明显分成两段直线(见图8b),斜率小的一段代表岩心含水饱和度变化主要受洞含水饱和度的影响,表明洞含水饱和度变化对系统电阻率的影响较小;斜率大的部分代表岩心饱和度变化主要受基质孔隙含水饱和度的影响,表明对电阻率敏感的是基质孔隙中的含水饱和度变化。如果忽略洞对电阻率的影响,大部分数据点的变化趋势完全符合Archie公式。

图8 实验样品照片(a)及含水饱和度与电阻率关系曲线(b)
数值模拟与实验测试结果均证明了洞含水饱和度与研究对象电阻率关系不大。对于孔洞型储集层,可将基质孔隙和洞分开研究,基质孔隙的电阻率满足(13)式和(14)式,洞的电阻率满足(15)式和(16)式。
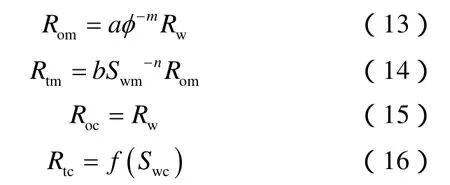
为建立f(Swc)的具体表达式,假设洞为圆柱形,地层水在洞中以水膜形式存在,已知电阻与电阻率的关系式为:

洞中水膜部分的电阻率用微元法推导,表达式为:
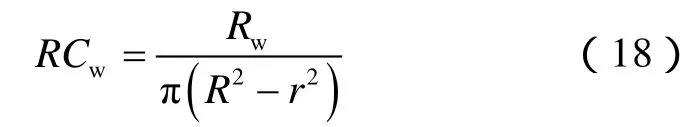
通常情况下考虑气体为绝缘体,则洞中含气部分的电阻率可以视为正无穷大:

对于整个洞的电阻率可通过并联方式求解:
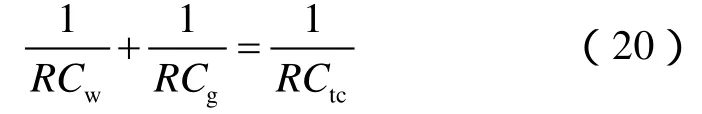
将(18)和(19)式代入(20)式求解可得:

(21)式的物理意义为洞电阻率等于地层水电阻率与洞含水饱和度的比值。地层水电阻率通常为 0.1Ω·m,基质孔隙的电阻率通常为50~1 000 Ω·m,只有当洞电阻率与基质电阻率相近时,洞电阻率才会对研究对象的电阻率构成影响。在洞电阻率远小于基质电阻率的情况下,二者存在(22)式的关系,其物理意义为,研究对象电阻率等于基质电阻率与基质在研究对象中体积占比的乘积。

数值模拟和实验分析以及理论推导均证实,洞中的水在减少至趋近于 0之前,对研究对象的电阻率不会有太大影响。因此,针对孔洞型储集层,根据电阻率变化来确定整个储集层中岩石含水饱和度是很困难的。对于部分含水的孔洞型储集层,(22)式具有两层含义:①基质电阻率与孔洞型储集层电阻率只相差一个系数,该系数的大小与洞孔隙度成反比,洞孔隙度越大,储集层电阻率就越低;②基质含水饱和度与基质电阻率的变化规律仍旧满足Archie公式,表明基质含水饱和度是决定孔洞型储集层电阻率的关键因素。
3.2 孔洞比与电阻率的关系
孔洞比定义为基质孔隙度与洞孔隙度的比值。在数值模拟中,孔洞型储集层中的洞满足如下假设条件:①洞与洞之间相互孤立,只能通过基质孔隙连通;②孔与孔之间直接连通,也与其相邻的洞相互连通;③洞与其相邻孔直接连通,但与周围的洞不直接连通。孔洞比越大,则基质孔隙度占比越大。假设岩石孔隙100%饱和地层水,通过构建网络模型,模拟计算不同孔洞比与研究对象电阻率的关系(见图9)。在孔隙度相同的情况下,研究对象电阻率越大,孔洞比越低,意味着基质孔隙占比越小。在同一孔洞比100%饱和盐水条件下,总孔隙度越大,电阻率越低。在电阻率相等的情况下,总孔隙度越大,孔洞比越低,意味着洞孔隙度占比越大。
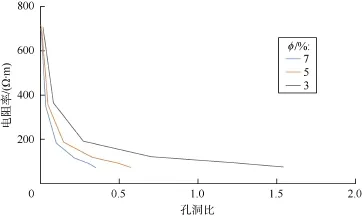
图9 孔洞比与研究对象电阻率关系曲线
在洞孔隙度大于某个阈值之前,基质电阻率的大小是决定储集层电阻率的关键。当基质孔隙度低到一定程度时会发生“高电阻率水层”现象。在储集层孔隙结构特征不清时,仅凭电阻率值的高低来解释储集层是否含水是不准确的,即使在 100%含水饱和度情况下,由于不同孔洞比的搭配关系,电阻率可能小于100 Ω·m,也可能超过500 Ω·m。同一电阻率在具有不同孔洞比的储集层中可以对应不同的含水饱和度。
4 结论
本文构建了孔洞型储集层岩石电阻率计算技术,解决了逾渗网络理论模型计算孔洞型储集层岩石电阻率运算量大的技术难题,为大溶蚀孔洞储集层电阻率计算提供了方法和手段。
确立了孔洞型储集层岩石电阻率与洞孔隙度之间的关系。含水溶洞孔隙度越大,储集层电阻率越小;当溶洞孔隙度大于一定阈值时,研究对象的电阻率呈现出接近地层水的特征。
建立了孔洞型储集层岩石电阻率与洞含水饱和度关系的数学模型,得到了溶洞含水饱和度与研究对象电阻率的关系。孔洞型储集层基质含水饱和度与电阻率满足Archie公式,溶洞含水饱和度对储集层电阻率的影响较小。
通过实验测定与数值模拟相结合,得到了相同孔隙度下不同孔洞比与研究对象电阻率的关系。在相同孔隙度条件下,储集层基质越致密,则研究对象的电阻率越大,有效解释了“高阻水层”现象。基质孔隙度和洞孔隙度占比以及基质孔隙含水饱和度才是决定储集层岩石电阻率的关键因素。
符号注释:
a、b——Archie公式中与岩性有关的岩性系数;A——圆柱形洞的横截面积,m2;E——电场强度,V/m;Ei,j——x方向上第i个、y方向上第j个节点的电场强度值,V/m;Ex——x方向上的电场强度分量,V/m;Ey——y方向上的电场强度分量,V/m;i——x方向上的单位向量;j——y方向上的单位向量;J——电流密度,A/m2;Je——位移电流密度,A/m2;Jx——电流密度在x方向上的分量,A/m2;Jy——电流密度在y方向上的分量,A/m2;Jy,input——入口端电流密度y方向上的分量,A/m2;Jy,output——出口端电流密度y方向上的分量,A/m2;l——圆柱形洞的长度,m;m——Archie公式中的胶结指数,与岩石胶结情况和孔隙结构有关的指数;n——Archie公式中的饱和度指数;N——研究单位基本单元个数的平方根,自然数;Qj,v——一个单位体积里流出的电荷量,C/m3;r——圆柱形洞的横截面积中含气部分的直径,m;R——圆柱形洞的横截面积直径,m;RCg——圆柱形洞中含气部分的测试电阻,Ω;RCtc——圆柱形洞饱和盐水和烃类物质时的测试电阻,Ω;RCw——圆柱形洞中水膜部分的测试电阻,Ω;Roc——洞100%饱和盐水时的电阻率,Ω·m;Rom——储集层基质 100%饱和盐水时的电阻率,Ω·m;Ros——研究对象100%饱和盐水时的电阻率,Ω·m;Rtc——洞饱和盐水时的视电阻率,Ω·m;Rtm——饱和地层水和烃类物质的岩石基质孔隙的电阻率,Ω·m;Rts——研究对象饱和盐水和烃类物质时的电阻率,Ω·m;Rw——地层水电阻率,Ω·m;Swc——洞含水饱和度,%;Swm——基质孔隙含水饱和度,%;U——电势差,V;σ——电导率,S/m;σi, j——x方向上第i个、y方向上第j个节点的电导率值,S/m;φ——孔隙度,%;φc——洞孔隙度,%;φcc——洞孔隙度阈值,%;ρ——电阻率,Ω·m;κ——研究对象数值模拟过程中y方向上划分的网格数。
