基于板-梁理论的桁架拱整体稳定分析

华俊凯，张文福,，赵文艳，黄斌，詹阳，计静

（1.苏州科技大学，江苏 苏州 215000；2.南京工程学院，江苏 南京 211167；3.东北石油大学，黑龙江 大庆 163318）

0 引言

大跨度桁架拱结构作为桥梁和大跨度建筑重要的支承结构，在工程领域已有广泛应用，但其设计理论体系仍未完善。

目前对于实腹式拱结构的稳定性分析较多，对于平面桁架拱的研究还较少。 以平面桁架圆管钢拱为研究对象， 如图1 所示， 其中R 为圆拱半径，θ 为圆心角，S 为圆拱弧长，h 为桁架截面上下弦杆形心之间的距离。 取平面桁架单一节间进行分析， 将斜腹杆按扭转刚度等效原则等效为腹板后，基于板-梁理论求出平面桁架的抗弯、抗扭以及翘曲刚度。 利用ANSYS 对不同跨径比的轴压和纯弯铰支拱进行有限元建模与分析，验证所给出的截面参数的正确性。

图1 桁架拱

1 弯扭屈曲应变能及截面参数

1.1 板-梁理论

板-梁理论是由张文福[1-4]教授提出的薄壁构件组合扭转以及弯扭屈曲问题的新工程理论。其基本假设为：①刚周边假设；②板变形假设；③梁变形假设。 对于开口截面构件，将薄壁板件的变形分为扭转变形和弯曲变形， 分别用Kirchhoff 薄板理论和Euler 梁理论进行分析。 对于扭转变形，令其遵循刚周边假设。

1.2 腹杆的等效

对于细长的平面桁架，腹杆主要抵抗扭矩的作用，因此令腹杆对形心的抗扭刚度等效为腹板的抗扭刚度，可得

即

可解得等效腹板的厚度tw为

式中：G为材料剪切模量；It，f3和It,w分别为腹杆和等效腹板截面极惯性矩；Df3为腹杆外径；hw为等效腹板高度；αf3=df3/Df3为腹杆内外径之比。

1.3 等效腹板应变能

1.3.1 等效腹板截面任意点的位移

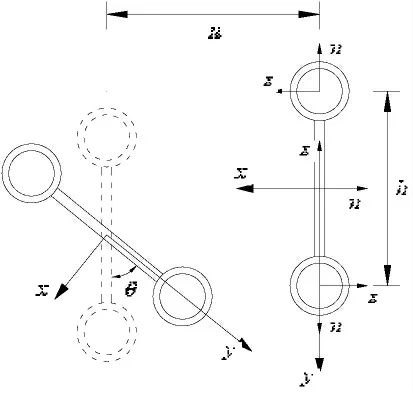
图2 截面变形

如图2 所示，腹板局部坐标系轴与截面整体坐标系x轴之间的夹角为α，腹板截面任意点在局部坐标系下的坐标 （n，s） 和整体坐标系下的坐标（0，0）之间的关系可表示为

腹板截面任意点（n，s）沿n，s轴方向的位移μn,w、μs,w及截面形心绕z轴的转角θw可表示为

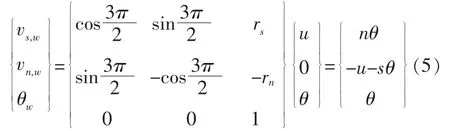
其中

可得腹板形心位移为

其中，u0w、v0w、w0w分别为腹板形心沿着局部坐标系n轴、s轴、z轴方向的位移。

1.3.2 等效腹板的平面内弯曲应变能

根据变形分解原理，腹板平面内位移可分解为

沿着n轴的位移

沿着s轴的位移

纵向位移由Euler 梁模型来确定

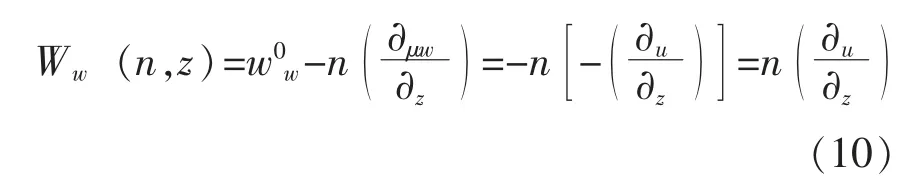
平面内弯曲的几何方程

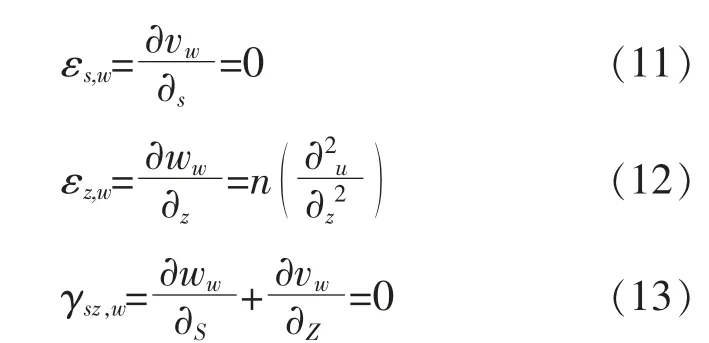
平面内弯曲的物理方程

则应变能根据

可得

其中，E为材料弹性模量。

1.3.3 等效腹板的平面外扭转应变能

根据变形分解原理，腹板平面外位移可分解为：

沿着n轴的位移

沿着s轴的位移

纵向位移由Kirchhoff 薄板模型来确定

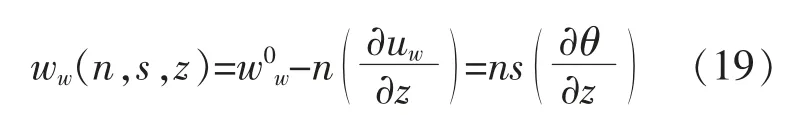
平面外弯曲的几何方程

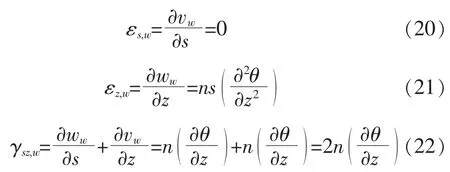
根据物理方程式（14），可得平面外弯曲应变能为

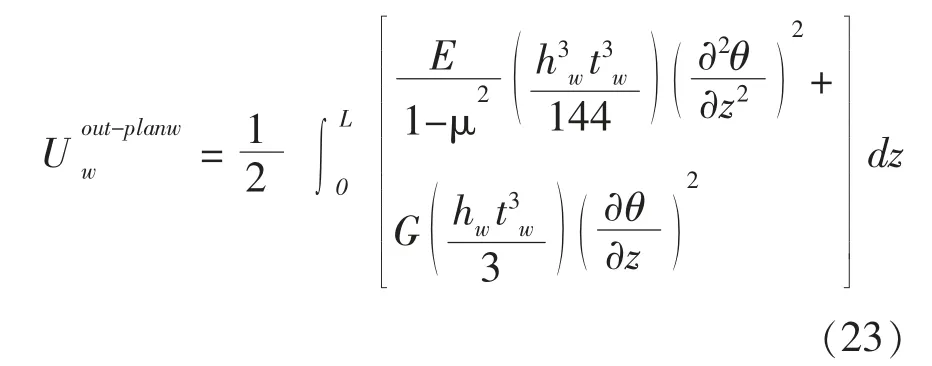
1.4 弦杆弯扭屈曲应变能

与腹板求解过程相同， 上弦杆平面内弯曲的应变能为

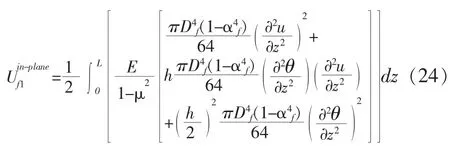
其中，Df为弦杆外径；αf=df/Df为弦杆内外径之比。

上弦杆平面外弯曲的应变能为

下弦杆平面内弯曲的应变能为

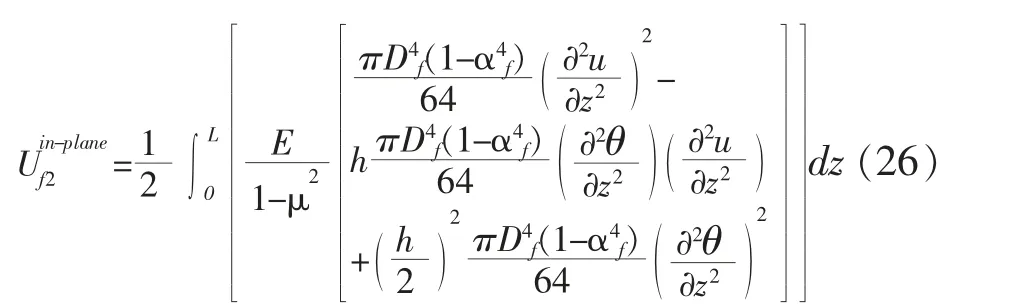
下弦杆平面外弯曲的应变能为

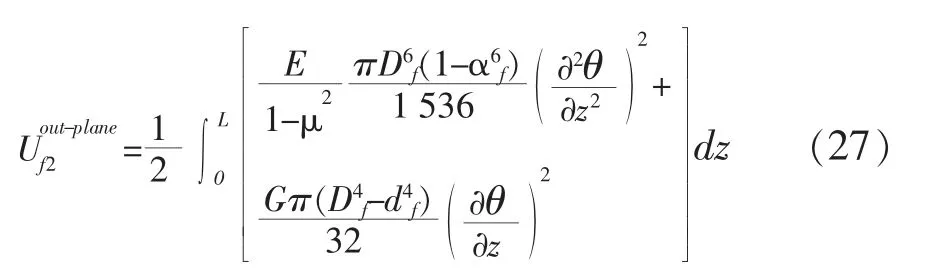
则平面桁架拱单一节间弯扭屈曲的总应变能为

令

为平面外抗弯刚度；

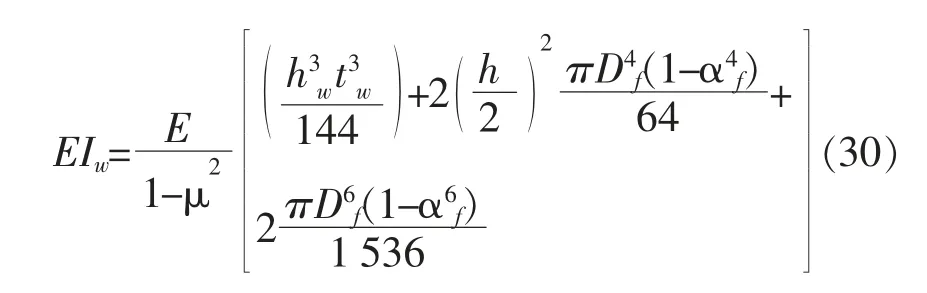
为截面翘曲刚度；

为截面自由扭转刚度。

则可将应变能转化为一般形式，即

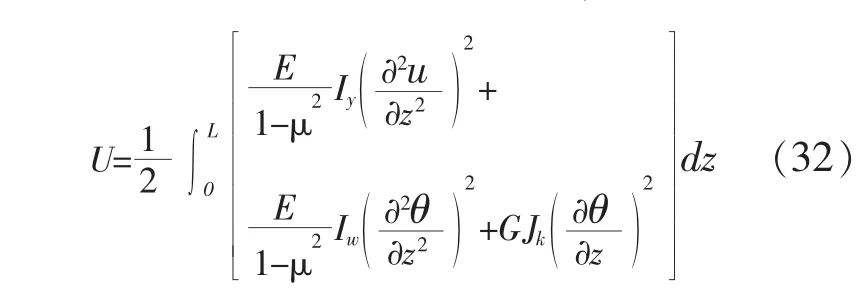
2 桁架截面参数的简化算法

平面桁架拱截面参数的简化算法如下

其中，Iyc为弦杆截面惯性矩。

其中，It，c为弦杆截面极惯性矩。

3 桁架拱平面外弹性屈曲极限承载力

桁架拱与实腹式拱在稳定的平面外变形情况上并无明显区别， 因此可以沿用实腹式拱平面外稳定性的极限荷载公式。 简支拱受力情况如图3所示。

图3 截面变形

为模拟理想的简支拱受压与受弯情况，令一拱脚可沿法向滑动。

3.1 纯压作用下的极限承载力

实腹式拱在纯压作用下的弯扭屈曲极限荷载Nysa为

其中，kysac为纯压拱的平面外屈曲系数， 其表达式为

其中，

式中，Mys为简支梁在纯弯矩作用下的平面外屈曲极限荷载；Ny为简支柱在轴压作用下的屈曲荷载；Ns为简支柱在扭转作用下的屈曲荷载。

3.2 纯弯作用下的极限承载力

拱在纯弯矩作用下的弯扭屈曲极限荷载Mysa为

其中，kysam为纯弯拱的平面外屈曲系数，其表达式为

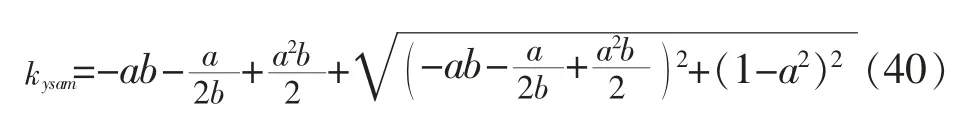
求解纯弯拱平面外屈曲方程可得

4 有限元对比验证

为验证求解的截面参数与简支拱平面外屈曲极限承载力的正确性，用ANSYS 建立有限元模型，模型采用BEAM188 单元，分别建立不同径跨比的简支桁架拱。 相关截面尺寸与径跨比如表1 所示。

4.1 轴压拱弯扭屈曲荷载公式验证

将式（29）-（31）和式（33）-（35）计算所得的桁架节间截面参数分别代入式（36）-（39），计算桁架拱平面外屈曲荷载，与有限元分析结果对比（假设有限元结果为精确解），如表2 所示。

由表2 可知，式（29）-（31）计算结果更能准确地反映截面性质，腹杆对于整体截面刚度有较大影响。

表1 有限元模型参数

表2 轴压拱平面外屈曲荷载

4.2 纯弯拱弯扭屈曲荷载公式验证

对于纯弯简支拱，将式（29）-（31）分别代入式（40）和式（41），并与有限元结果对比，如表3 所示。

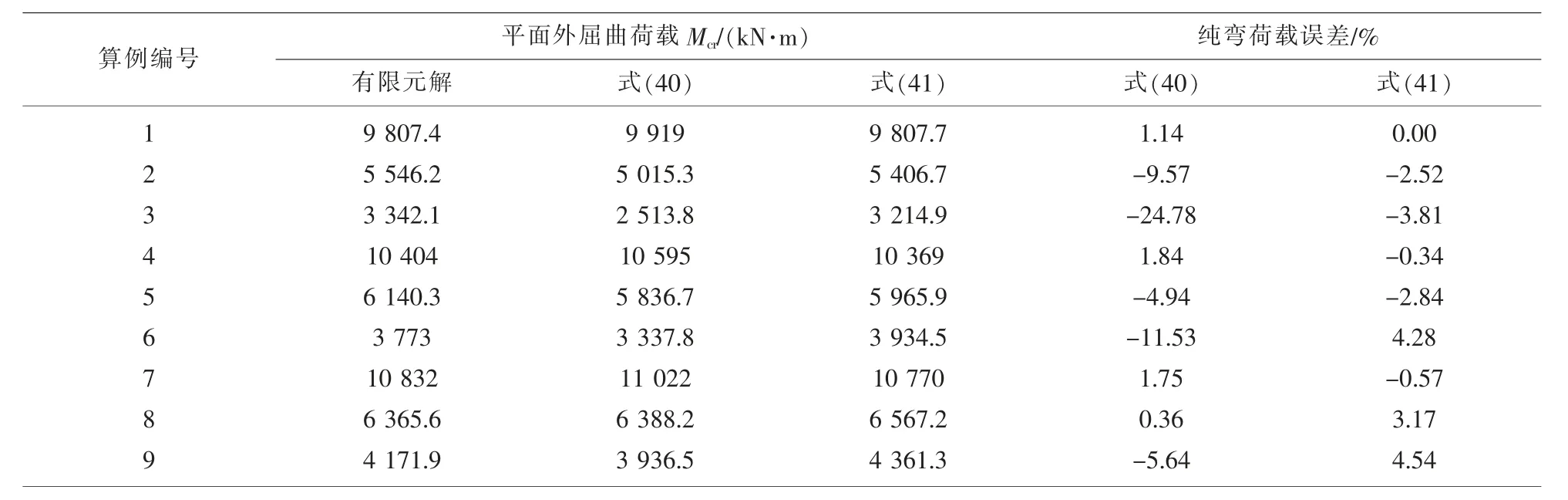
表3 纯弯拱平面外屈曲荷载

由表3 可知，在一般情况下式（40）和（41）的平面外屈曲荷载公式都具有良好的精度。但对于细长构件，式（40）计算结果误差可达24.78%，不能真实反映简支桁架拱的力学性能。

5 结论

（1）平面桁架拱在平面外变形过程中具有与实腹式拱相同的受力及变形特点，因此实腹式拱的平面外稳定理论可以应用于平面桁架拱。

（2）板-梁理论无需运用传统的扇性坐标，能精确推导出薄壁构件的各类截面参数； 腹杆对于平面桁架抵抗弯扭屈曲具有较大帮助。

（3）式（40）和式（41）的平面外屈曲荷载公式都具有良好的精度，但不能用于细长的纯弯简支拱平面外屈曲荷载计算。