基于改进遗传算法的客运站到发线运用优化研究

2020-06-30张杉基孙建林

铁道运输与经济 2020年6期

李涛，张杉基，孙建林，张杨，贾飞

LI Tao, ZHANG Shanji, SUN Jianlin, ZHANG Yang, JIA Fei

（兰州交通大学交通运输学院，甘肃兰州 730070)

0 引言

到发线分配是客运站行车作业的一项重要内容，是车站阶段计划编制的关键工作之一。到发线的合理运用不仅关系车站的正常运输生产和运行图的实现，还关系铁路行车安全和列车运行的经济效益。一般情况下，客运站按照到发线的固定使用方案接发列车，而在实际运营中，列车的运行会受到恶劣天气、车辆及设备故障、节假日客流高峰等因素的影响而发生晚点，需要调整原有的到发线运用计划，尽可能保证车站作业顺利进行。为此，到发线的运用应保证客运站可以不间断地接发列车，最大限度地利用车站到发线的能力，同时也需要留有一定的余地，避免高峰时段列车在站外停车等线导致的晚点传播。因此，研究列车到发时刻波动情况下客运站的到发线运用问题，对客运站到发线运用计划编制有非常重要的意义。

为了高效、合理地运用到发线，保证接发车作业的效率，许多学者对到发线的运用优化进行研究。部分研究[1-3]建立客运站到发线运用的0-1 规划模型，实现客运站到发线运用计划的自动编制，但均未考虑设备使用的均衡性。部分研究[4-6]把客运站到发线运用优化的目标分解为3 个子目标，其中谢楚农等[4]建立多目标优化模型，采用分枝定界法求解；林志安等[5]运用捕食禁忌搜索求解；吴鹏等[6]统一多目标函数的量纲，将多目标优化问题转化为单目标优化问题，利用分枝定界算法求解。当问题规模较大时，谢楚农等[4]和吴鹏等[6]提出的方法无法满足求解效率要求。刘伟等[7]统计列车实际到发时刻的均值和方差，建立满足列车、咽喉及到发线耦合关系的模型，采用模拟退火算法求解。刘伟等[8]考虑安全约束，建立晚点情况下客运站到发线分配模型，分析延误时间与延误列车数量的关系。部分研究[9-11]建立车站到发线运用的排序模型。Billionnet[12]把到发线运用优化问题描述为有权重的NPP，构造无向图，采用分枝定界法求解。

这些研究大多是按图定到发时刻对客运站到发线运用进行优化，对实际运营中列车到发时刻波动的研究较少。按照图定到发时刻计算得到的到发线运用方案没有充分考虑列车晚点的情况，鲁棒性较差，在列车到发时刻不确定的场景下使用效果不佳，需要频繁地调整车站到发线运用计划。因此，考虑列车到发时刻不确定性，运用概率统计和不确定理论，统计得到实际运营中列车到发时刻的波动范围，建立客运站到发线运用优化模型。借鉴模拟退火算法思想，改进遗传算法的选择算子，避免算法过早收敛或过慢结束，同时提出交叉概率的自适应确定方法，加快遗传算法的收敛速度。该模型和算法可以实现有预见性地安排到发线运用，减少交叉干扰产生的列车晚点，提高作业的安全性。

1 客运站到发线运用问题

1.1 问题假设

在列车到发时刻波动条件下，对铁路客运站到发线优化模型作出以下假设：①列车在运行过程中不发生铁路交通事故及其他安全事件；②站内的到发线、信号机等设备能正常接发列车，站外的线路等设备可以保证列车正常运行；③列车运行时间发生波动，不会使列车到达车站的次序发生变化；④不考虑大面积晚点以及列车停运的情况。

1.2 列车到发时刻波动范围

列车到发时刻服从的分布无法预先掌握，也很难对其分布作出准确的假设，可以根据经验或专家的意见，预测其大致的趋势，再用已有的样本数据对预测的分布形态进行验证。基于非参数检验方法，先采用数理统计方法，对一定时段内的列车到发时间波动值(列车实际到达时刻与计划到达时刻之差)进行统计，根据该时段波动值出现的次数以及专家的意见，假设其可能服从的分布，然后运用假设检验方法验证假设的合理性，即验证列车的到发时间波动是否服从该分布。如果假设检验不通过，则需要提出新的分布，再进行假设检验，直到得到合适的分布函数为止。最后，运用区间估计得出到发时刻的波动范围。由于区间的长度、同等级列车的运行速度相近，假设列车到发时刻的波动服从正态分布，假设问题的接受域为H0：列车i到达时刻的波动值服从正态分布，可以得到正态分布均值计算公式为

式中：为列车到达时刻波动值均值的估计值；n为研究阶段内相同等级的列车数量；i为列车序号；ti为第i列车的到达时刻波动值。

正态分布方差计算公式为

式中：为列车到达时刻波动值方差的估计值。

为提高统计的准确性，规定在通常情况下，样本容量n应满足n≥46。以到达时刻为例，用公式 ⑴ 和公式 ⑵ 分别计算列车到达时刻波动值的均值和方差，由此可以得到第i列车到达时刻波动值的正态分布估计，即ti～N(，)，然后用χ2检验进行验证。列车实际到达时刻与图定时刻通常存在一定的偏差。列车的到达时刻在指定的偏差范围内，可以认为其正点运行，该情况可以用公式⑶ 表示。

式中：为列车实际到达时刻的估计值；Ti为列车计划到达时刻；α为到达时刻偏差的允许范围；β为偏差的置信度。

为了得到列车到达时刻的波动范围，首先需要得到列车到达时刻波动值服从的分布函数，然后运用区间估计，对一定置信度水平下的波动范围进行估计。在列车到达时刻的波动值服从正态分布的情况下，如果公式⑶成立，则列车i的实际到达时刻在一定置信度水平下的波动范围可以用以下公式计算

式中：为对应分布的分位点。

2 客运站到发线运用优化模型

2.1 符号及变量

设客运站到发线的集合为D= {1，2，…，j，…，m}，其中j为到发线的编号，m为到发线的总数。计划阶段到达客运站的列车集合为L= {1，2，…，i，…，n}，其中i为列车到达车站的顺序，n为列车总数。客运车站作业种类的集合为P= {1，2，…，p，…，w}，其中p为作业种类编号，w为作业种类总数。

为第i列车占用到发线的总时间，计算公式为

式中：为信号员或车站值班员开始为第i列车排列进路，至列车完全停靠在到发线上所耗费的时间[4]，根据车站作业标准，为2 min；为列车从完全停靠在到发线时起，至该列车从车站出发时刻止，列车在到发线上所停留的时间，其取值由图定的列车到达时刻和出发时刻确定；为列车从出发时刻起，至该列车完全离开该进路止所耗费的时间[4]，根据车站作业标准，为2 min[13]。

cij为列车i占用到发线j的权值，确定方法与吕红霞[14]相同。Lij'为0-1 已知量，取值为1 时表示到发线j与到发线j'相邻，共用同一个站台，取值为0 时反之；Sii'为0-1 已知量，取值为1 时表示列车i与列车i'存在换乘关系，取值为0 时反之。和分别为第i列车的计划到达和出发时刻。xij为0-1 变量，取值为1 时表示列车i占用到发线j，取值为0 时反之。hijp为0-1 变量，取值为1 时表示列车i占用到发线j时与作业p产生交叉干扰，取值为0 时反之。为列车i开始占用到发线的时刻；为列车i完全离开到发线的时刻。和分别为第i列车实际到达和出发时刻的估计值。

2.2 优化模型

客运站到发线运用的优化是合理安排列车到发线，使车站可以正点接发列车，避免列车由于等待到发线腾空造成的晚点，高效地完成运输生产任务。因此，客运站到发线优化模型的目标函数包含缩短旅客列车在到发线的停留时间(所有到发线占用时间总和)和均衡使用到发线(到发线占用时间标准差)2 部分。客运站到发线运用数学优化模型如下。

公式 ⑹ 为目标函数，表示所有到发线占用时间总和和到发线占用时间标准差之和最小。公式 ⑹ 至 ⑾ 为约束条件。公式 ⑺ 至 ⑻ 表示在任何情况下，所有列车占用到发线时都必须遵循的约束。其中，公式 ⑺ 表示每列车必须且只能选择1条到发线，该列车在出发之前不能转移到其他到发线上；公式 ⑻ 保证同一条到发线上先后接发的2列车时的安全，避免2 种车站资源占用冲突情况，冲突示意图如图1 所示；公式 ⑼ 表示列车到达时刻机会约束。列车i实际到达时刻发生了波动，已不再是一个确定的值，其到达时刻是在一定置信度水平下的置信区间，约束中用其估计值；公式⑽表示交叉的疏解[13]，在同一个时间片[1]内，接发列车的进路不能有冲突(如列车的接发与机车出入段的交叉)，应多组织平行作业来减少交叉干扰；公式⑾表示把存在换乘关系的列车安排在相邻的站台上[13]。

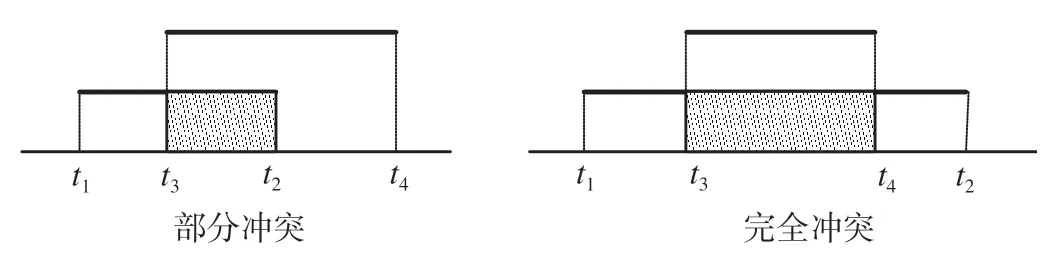
图1 冲突示意图Fig.1 Conflict diagram

因为列车进站、出站作业时间以及在站停留时间几乎都是固定的，且列车的到达时刻发生了波动，所以列车出发时刻的估计值可以用列车到达时间的估计值与列车占用到发线的总时间之和表示，即为此，公式 ⑻ 可以化简为

对于列车到达时刻的机会约束，根据列车到达时间波动范围的确定方法，将其转化为以下对列车到达时刻进行估计的约束

3 改进遗传算法

3.1 改进遗传算法流程

到发线的运用优化已经被证明属于NP 完全问题[11]，对该类问题的求解目前还没有被证明的多项式时间算法，求解的难度较大，因而此类问题多采用智能算法求解。虽然考虑了列车到发时刻波动的置信区间，同时加入了机会约束，但是列车占用到发线的过程和图定到发时刻下列车占用到发时刻的过程呈现一致性，因而采用智能算法求解仍然可行。因此，在常规遗传算法中融入模拟退火(Simulated Annealing，SA)的思想，对适应度函数和交叉算子进行改进，采用改进的遗传算法进行求解，较好地解决经典遗传算法易早熟和局部搜索能力差的缺点，提高了运行效率和求解质量。改进遗传算法流程图如图2 所示。

图2 改进遗传算法流程图Fig.2 Improved genetic algorithm

3.2 适应度函数

适应度函数求取的是极大值，并且适应度函数的值大于或等于0。根据实际问题的特性，以目标函数的取值作为适应度的计算依据，并且在目标函数中加入惩罚系数，得到以下适应度计算公式

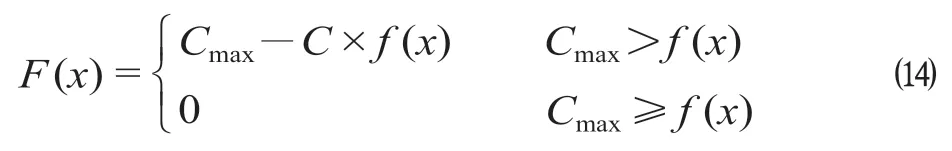
其中

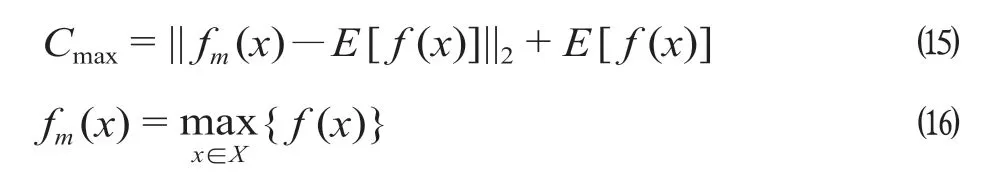
式中：fm(x)是当前输入空间个体的最大值；E[f(x)]是目标函数的均值；用fm(x)和E[f(x)]之差的欧氏范数再加上E[f(x)]作为Cmax的取值；C为惩罚系数，当有2 列及以上列车在一个时间片内占用同一到发线时，C= 1，否则C= 1/1000[13]。

3.3 改进选择算子

遗传算法常用赌轮选择法作为选择算子。该方法容易用程序实现，但是在计算过程中存在过早收敛或过慢结束的现象。为了解决此问题，首先创建了两个种群大小均为N的空间，并把二者按其适应度的大小分别进行排序；然后把父代种群中1/4 的最优个体和子代种群中1/2 的最优个体组合成一个新的种群，对新种群进行退火选择；最后从中间选取N个个体组成新的父代，再进行后面的交叉和变异操作[15]。如果个体的适应度大小为f(i)，则个体i被选中的概率为

式中：tk= 1 / ln (kt0+ 1)为当前状态的退火温度；t0为初始温度；k= 1，2，…。

3.4 交叉算子自适应调整

遗传算法中交叉概率Pc的取值对算法的收敛性和搜索速度有很大影响，选取不当会使算法进化缓慢，破坏种群的多样性，使算法陷入局部最优。因此，交叉概率进行非线性的指数形式调整[16]为

式中：K1= 0.5，K2= 0.9；favg是每代种群适应度的平均值；f '是当前需要交叉的2 个个体中适应度较小的一个个体；fmin是每代种群中最小的适应度。

图3 列车到达时刻波动直方图Fig.3 Train arrival time fluctuation histogram

4 算例分析

4.1 模型求解

为了验证改进遗传算法和建立模型的准确性，选取某客运站8 : 00—12 : 00 的数据进行验证。该站共2 条正线，5 条到发线，其中3，5，7 号到发线固定接发下行列车；4，6 号到发线固定接发上行列车；正线I，II 分别用于下、上行列车的不停站通过。选取阶段中到发的列车共46 列。种群大小为30；变异概率pm= 0.01；最大迭代次数U=500；初始温度t0= 100，当温度低于10 时，采用等步长下降[17]，步长取1。

通过统计数据可知，由于客运站7—9 月雨水较多，而且铁路旅客运输周期性波动明显，对车站的行车作业有较大的影响，也对车站工作计划的鲁棒性要求较高。为此，统计这3 个月的数据来验证改进遗传算法和模型的合理性。经统计，得到某站7—9 月8 : 00—12 : 00 的46 列列车的波动时间，通过假设检验的内容可以得到列车到发时刻的分布，借助IBM SPSS Statistics 23 进行验证，样本的均值为0.78，标准差为5.723。列车到达时刻波动直方图如图3 所示。

由图3 可知，除了1 列车的时间波动以外，其余列车到达时刻的波动是近似服从正态分布的。运用单样本柯尔莫哥诺夫-斯米尔诺夫检验(K-S检验)对文中的假设进行验证，得到列车到达时刻波动的正态Q-Q 图如图4 所示；列车到达时刻波动的假设检验摘要如表1 所示。

图4 列车到达时刻波动的正态Q-Q 图Fig.4 Normal Q-Q graph of train arrival time fluctuation

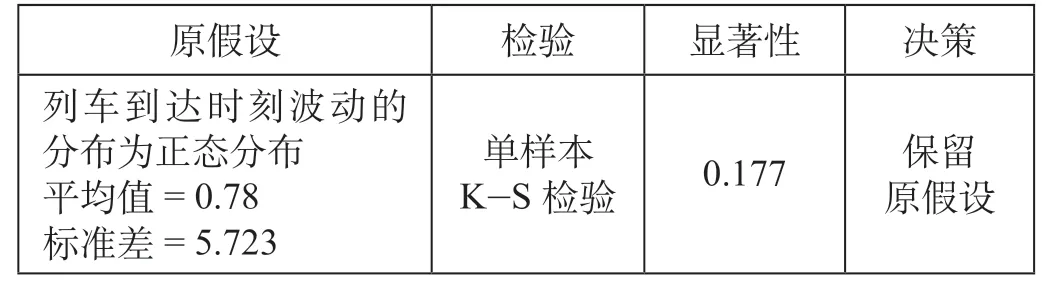
表1 列车到达时刻波动的假设检验摘要Tab.1 Summary of hypothesis test for the train arrival time fluctuation

由图4 可知，数据与对角线基本重合，Q—Q 图提示该组数据服从正态分布；而单样本K—S 检验数据摘要中显著性概率0.177 ＞ 0.05，决策为“保留原假设”，即列车到达时刻的波动值服从正态分布。从现场得知，该客运站高速列车的正点率是96%，因而该站列车正点到发的置信度为96%，从而得到列车到达时刻的波动范围[-1.73，1.76]，取整后为[-2 min，2 min]。利用改进遗传算法为8 : 00—12 : 00 到达的列车分配到发线，运用MATLAB 2018a在Intel Core i5-4210H CPU (2.90 GHz)，内存4G 的计算机上求解，得到稳定的目标函数值为49 969 min。改进遗传算法优化收敛趋势如图5 所示；到发线运用方案如表2 所示。

图5 改进遗传算法优化收敛趋势Fig.5 Improved genetic algorithm optimizes the convergence trend

表2 到发线运用方案Tab.2 Scheme for arrival-departure tracks utilization

4.2 结果分析

（1）均衡性分析。从算例结果可以看出，所设计的模型和算法可以满足列车在车站的作业需要，上行列车分布在4，6 股道，下行列车分布在3，5，7 股道。根据均衡性评价的定义，均衡度的计算公式为

根据公式 ⒆，分别计算车站值班员用的方案和优化模型得到的到发线运用方案均衡度如表3所示。

（2）波动误差分析。随机选取15 列列车，根据计算得到的波动值，计算列车的最早到达时刻和最晚到达时刻。波动下列车最早和最晚到达时刻如表4 所示。由表4 可知，列车在波动范围内占用到发线的估计最早到达时刻或最晚到达时刻与实际到达时刻的误差ΔT1= 41 min；而不考虑列车到达时刻波动的列车到达时刻误差ΔT2= 61 min。比较考虑波动与不考虑波动下到达时刻的误差值可知，考虑列车到达时刻波动能更好的描述列车的实际到达时刻，波动误差值减少了33%。