基于分数阶微分模拟模型的油田措施增产预测
2020-06-30刘志斌马南南
肖 武,韩 丹,刘志斌,陈 琳,马南南
(1.中石化股份公司胜利油田分公司勘探开发研究院,东营 257000;2.中国石油冀东油田分公司陆上油田作业区,唐山 063004;3.西南石油大学理学院,成都 610500)
石油是国家的战略能源,中国油藏地质构造复杂。油藏类型多样,如浅层天然水驱油藏、中、深层注水开发油藏、深层低渗透油藏、溶解气驱油藏、潜山碳酸盐岩等。当油田开发达到一定阶段时,为了增加产量必须实施增产措施,不同类型油田所需的增产措施不同[1]。常见的措施有二氧化碳吞吐、压裂、酸压、解堵、反抽等,每种措施的增产效果受多种因素的影响[2-3]。增产措施效果直接影响油田的经济效益,较准确地预测措施增加产量可以对油井准确实施合适的增产措施,从而使油田的效益最大化[4-5],所以措施增产预测对油田的高效开发具有重要的意义。
多因素灰色预测模型被Deng[6]提出后就一直被改进。一些学者改进了单变量线性灰色模型,Wang等[7]提出了一种改进的灰色预测模型PRGM(1,1),集成了粒子群优化算法和数据指数预处理方法从而扩展了预测模型的适用性。Wei等[8]将背景系数引入灰色多项式模型,提出了多项式阶数选择、背景系数搜索和参数估计的算法框架,推导了累加序列仿射变换与参数估计之间的定量关系。Wang等[9]建立了灰色Verhulst模型,为了避免在建模理论中代入微分方程的差分方程产生的误差,推导了非等间隙模型,并将微分模型应用于研究CO2排放与经济增长的关联关系。Ayvaz等[10]为了准确预测电量消耗提出了非齐次离散微分模型并验证了模型的有效性。随着发展单变量非线性灰色模型也得到了改进。Wang等[11]为了准确预测中国具有非线性小样本特征的高科技企业的主要经济指标,提出了一种优化非线性灰色伯努利模型求解最优参数最终建立了优化模型。Wu等[12]提出了一种将灰色累积生成技术与Holt-Wins方法相结合的空气质量指数预测模型,提高了空气质量指标预测精度。Wang等[13]采用非线性最小二乘法建立了灰色Bass模型并给出了微分方程的白化解,解决了新产品扩散预测问题。Wu等[14]提出了一种基于灰色关联分析的最小二乘支持向量机模型,并设计了加权自适应二阶粒子群优化算法对模型参数进行优化,将模型成功应用到天然气消耗预测中。Ren等[15]提出了一种非等间距非齐次指数微分模型并成功应用于循环荷载作用下的累积塑性变形预测。Cui等[16]为了提高微分预测模型的预测精度,提出了一种新的灰色预测模型及其优化模型,建立了用最小二乘法求解新模型参数的计算公式,并利用微分方程进行推导,得到了微分模型的时间响应序列。但是预测指标往往受多种因素影响,所以一些学者对多变量非线性灰色模型进行改进。Zeng等[17]发现了传统多变量微分模型中建模机制、参数估计和模型结构是造成模型精度低下的三大主要原因,在传统模型基础上引入线性修正项和灰色作用量项来改进模型的性能,新模型具有更合理的建模过程和更稳定的结构,解决了传统模型的三个缺陷。Zeng等[18]提出了一种新多变量的基于动态背景值系数的微分模型,利用粒子群优化算法对动态背景值系数进行优化,推导出新模型的时间响应函数和最终恢复表达式,并用高斯函数对模型进行了证明和简化。Deng等[19]提出了一种信息单元的数值映射算法,将生物分子序列的基础转化为数学建模的数字序列。在此基础上,利用多元微分模型分析了小尺度碎片能量的动态变化趋势,了解了遗传信息的存在。Li等[20]建立了灰色关联分析与微分模拟联合模型,研究了区域协调发展系统中人口、资源、经济和环境系统之间的相互协调关系。Hsu[21]研究了多因素微分模拟模型,并将模型应用研究了台湾独立银行的破产概率与宏观经济的关联关系。Tien[22]指出了传统多因素微分模型利用一阶累加生成序列计算存在的问题,并提出了通过卷积积分或用初等函数拟合模型项来建立正确的模型。
当预测指标受多因素影响时,多种因素的时间序列变化规律就决定了预测指标的变化趋势,一阶累加生成个算子(1-AGO)一般用于灰色预测模型中的初始数据处理,此种处理方式是将新旧时间序列数据的影响程度同等对待,但是不同时期的影响因素数据可能对预测指标的影响程度不同,为了权衡影响因素新旧数据对预测指标的影响程度分数阶累加生成算子被提出。Mao等[23]提出了一种扩展的单因素分数阶灰色预测模型,Yang等[24]通过利用傅里叶级数表示残余项从而改进了分数阶灰色预测模型的预测性能,其他学者也改进了分数阶灰色预测模型[25-28]。
灰色预测模型参数的确定一般采用最小二乘法[29-31],但是否是误差平方和越小对应着指标预测误差也就越小。误差平方和中误差项越大所起到的作用越大,而误差项越小所起到的作用越小。当存在异常值时,模型与整体定律的偏差明显。当系数较大时,数据与全律的变化随数据值的增大而增大,所以进一步优化模型的参数是必要的。
基于调研研究发现参数优化下的多因素分数阶微分模拟预测模型研究较少,提出一种基于参数优化的多因素分数阶微分模拟预测模型,旨在建立一种多因素下措施增产预测模型,以便为措施的评价与措施优化提供研究基础。首先建立多因素分数阶微分模拟系统模型,并给出模型参数求解方法和参数与分数阶优化的方法;综合考虑油田实际的措施增产监测数据、数据统计的可行性及数据参数变化规律,确定影响二氧化碳吞吐措施与压裂措施增产的主要影响因素,并将建立的微分模拟进行措施增产预测,利用部分措施增产数据进行模型参数训练,利用其余增产数据验证模型的预测情况,通过评价模型计算结果证明微分模拟模型预测的有效性。
1 模型建立与参数优化
1.1 模型建立
定义:X(0)={x(0)(1),x(0)(2),…,x(0)(m)}为原始序列,m为变量的个数。X(r)={x(r)(1),x(r)(2),…,x(r)(m)} (r∈R+)为X(0)的r阶累加序列(r-AGO),r为阶数。其中:

k=1,2,…,m
(1)
(2)
(3)
式中:a、bi、u为参数,将式(3)代入式(2)中,令t=k,可以得到:
(4)
式(4)中:α1、αi、β为参数分别为
(5)
(6)
其中:
(7)
多因素分数阶灰色微分方程微分求解可得到第k+1个时刻的r阶预测值,结果如式(8)所示:
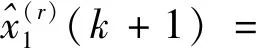
(8)
根据逆累加生成算子原理,可以得到第k+1个时刻的0阶预测值:
(9)
1.2 参数优化
1.2.1 分数阶微分模型参数优化
(10)
式(10)可以简写成为
(11)
式(11)中:
(12)
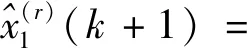
(13)
1.2.2 分数阶优化
在最小平均相对误差条件下,运用粒子群算法对分数阶微分模型的分数阶进行优化,目标函数如式(14)所示:
(14)
图1展示了粒子群算法的结构流程。运用粒子群算法[32]优化分数阶的步骤如下。

图1 粒子群算法优化结构流程Fig.1 PSOA program flowchart of fractional order optimization
步骤1随机初始化粒子群中粒子的位置和速度,一般可取pB=1。
步骤2将粒子中pB设置为当前位置,gB设置为最佳位置。
步骤3计算当r=pB时分数阶微分模型的平均相对误差F(pB),δ为给定的收敛值,如果|F(pB)-F(gB)|≤δ,则r=gB。如果|F(pB)-F(gB)|>δ,继续下一步。
步骤4更新粒子的位置与速度:
V=ωV+c1ra(pB-P)+c2ra(gB-P)
(15)
式(15)中:ωV为粒子的速度,ra为随机数,P为目前位置,c1、c2为学习因子。
P=P+V
(16)
(17)
如果粒子适应度优于pB,则pB设置为新位置,如果粒子适应度优于gB,则gB设置为新位置;
步骤5计算群体适应度方差σ2并计算F(gB)。
(18)
(19)
步骤6计算变异概率pm:
(20)
步骤7生成随机数ε∈[0,1],如果ε gBk=gBk(1+0.5η) (21) 步骤8如果ε≥pm,判断收敛准则是否满足,如果不满足转到步骤3,如果满足转向下一步。 采用三种统计准则对分数阶微分预测模型的预测性能进行了评价,分别是决定系数(R2)、根均方误差(RMSE)、平均绝对百分误差(MAPE)。R2用于识别观测数据值和模型预测数据值之间的拟合优度;RMSE是最常用监测预测值与观测值不一致的方法之一,可以指示模型预测的准确程度;MAPE常用于评估预测模型的整体预测性能。 (22) (23) (24) 式中:xi,e为实际观测值;xi,p为预测值;xi,a为实际观测值的平均值。 在油田开发的中后期,由于地层能量的损失油田产量递减逐渐严重,为了提高油田的产量保证油田的经济效益,必须对油井实施增产措施,油田的增产措施有多种,一般常规增产措施有二氧化碳吞吐、压裂、酸压、解堵、反抽等,不同措施对不同类型的油井增产效果不同,措施的优化选择决定了油井增产的效果和油田的经济效益,然而油田的措施优选的主要依据是措施的增产效果,所以油田措施增产准确预测可以为措施选择与优化提供重要依据。为此对二氧化碳吞吐与压裂两种措施增产预测进行了研究,影响二氧化碳吞吐与压裂增产的因素很多,包括剩余油饱和度、储层厚度、地层压力、黏度、自然裂缝渗透率、孔隙度、人工构造渗透率、人工裂缝长度、注采工艺等,但在一定时期内的采油过程中,有些因素保持不变或者变化非常微小,有些因素有一定变化且数据信息相对容易获得。综合考虑油井增产的所有因素,发现其内在联系可以准确预测措施增产,但准确获取所有影响因素的数据信息是困难或者说是不可能实现的。因此在研究二氧化碳吞吐与压裂措施增产效果预测时,仅选取了部分主要的影响因素数据作为控制变量,此处的主要影响因素个数可以根据油田措施增产实际采集数据信息进行调整,可以增加或者减少主要的因素个数。表1展示了选取的主要因素。 表1 措施增产主控因素Table 1 Main control factors for well stimulation 单因素分析法是研究油田措施增产预测的有效方法。为了研究油井增产措施对增加产量的影响,应研究同一口油井实施增产措施的增产情况,改变影响增产措施的单个变量,来观察增产效果,从而找到所有影响因素的作用效果。但油井增产措施实施周期较长且成本较高,利用单因素分析法研究措施增油预测模型几乎是不可能实现的。因此,选取了中国某油田同一区块同样地质类型且实施同种增产措施的多口油井进行措施增产预测研究。获取了油井2015—2016年24个月的连续监测数据,将每个月所有油井指标数据的平均值作为研究的数据值,得到了如表2、表3所示的实际数据信息。表2所示为二氧化碳吞吐措施增油量(x0)及影响二氧化碳吞吐增油量的主要影响因素剩余油饱和度(x1)、地层压力系数(x2)与吞吐轮次(x3)的关系。如表3所示压裂措施增油量(y0)及影响压裂措施增产的主要影响因素剩余油饱和度(y1)、储层渗透率(y2)与预计裂缝半长(y3)的关系。 表2 二氧化碳吞吐措施增产数据Table 2 Data on increasing production of CO2huff and puff 为了说明所建立的参数优化的分数阶微分模型(M3)预测效果,选取了多元回归模型(M1)与多元灰色系统预测模型(M2)两种传统的预测方法进行预测效果对比。所有模型均使用前18个月的措施增产数据进行模型参数训练,运用后6个月的增产数据对模型的预测效果进行评价。三种预测模型分别对二氧化碳吞吐与压裂增产措施增产进行了预测,增产预测结果如表4、表5所示。 表3 压裂措施增产数据Table 3 Data on increasing production of fracturing 表4 二氧化碳吞吐措施增产预测结果Table 4 Forecast result of increasing production CO2 huff and puff 续表4 表5 压裂措施增产预测结果Table 5 Forecast result of increasing production fracturing 从表4可以发现参数优化的分数阶微分模型(M3)在训练数据与预测数据的MAPE均小于其他两种模型的数值;模型M3的评价指标RMSE小于其他两种模型的数值,反映了M3模型的优越性;模型M3的R2更接近于1,说明模型M3预测效果较好;综合三种评价指标分析,在三种预测模型中模型M3对二氧化碳吞吐措施增产的预测效果最好。 从表5可以发现模型(M3)在训练数据的MAPE小于其他两种模型的数值;模型M3的评价指标RMSE与模型M2的RMSE非常接近且均小于M1模型的RMSE;三种模型的R2均小于0,说明三种模型的R2评价均不理想,但在MAPE值评价中模型M3的值最小,说明模型M3的预测误差在三者中最小,综合三种评价指标分析,在对压裂措施增产的预测中模型M3效果最好。 图2 各模型对二氧化碳吞吐措施增产预测Fig.2 Increased production prediction of CO2 huff and puff by each models 图2分别展示了模型M1、M2与M3对二氧化碳吞吐措施增产预测结果及预测值与原始数据的对比曲线。图3分别展示了模型M1、M2与M3对压裂措施增产预测结果预测值与原始数据的对比曲线,共有24组数据,其中前18组数据为模型参数训练数据,其余6组数据用于模型预测结果检验,从图3曲线可以发现模型M3的拟合与预测能力都优于其他两种预测模型,展现了M3模型对油田措施增产预测的优势。 图3 各模型对压裂措施增产预测Fig.3 Increased production prediction of fracturing by each models 为了解决油田措施增产预测问题建立了参数优化的分数阶微分模拟预测模型,通过模型建立与模型的实际应用及效果评价分析得到以下认识与结论。 (1)参数优化的分数阶微分模拟预测模型具有改变不同时间数据作用权重与优化预测性能提升的特点。 (2)通过预测性能的对比,参数优化的分数阶微分模拟预测模型预测性能优于一般的预测模型。 (3) 参数优化的分数阶微分模拟预测模型能对二氧化碳吞吐措施增产与压裂措施增产进行预测,说明模型具有一定的适应性,模型可以用来进行油田措施增产预测研究。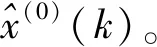
2 评价模型
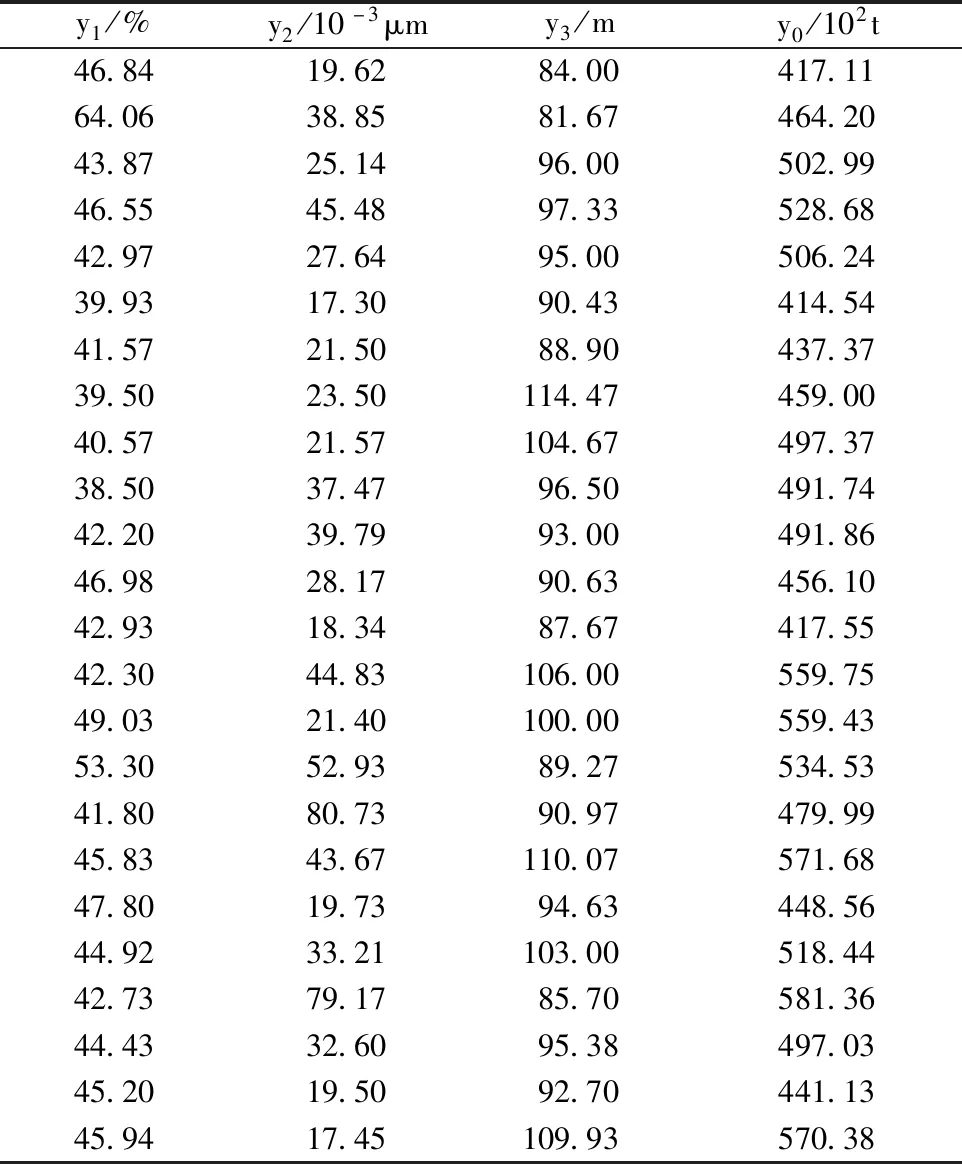
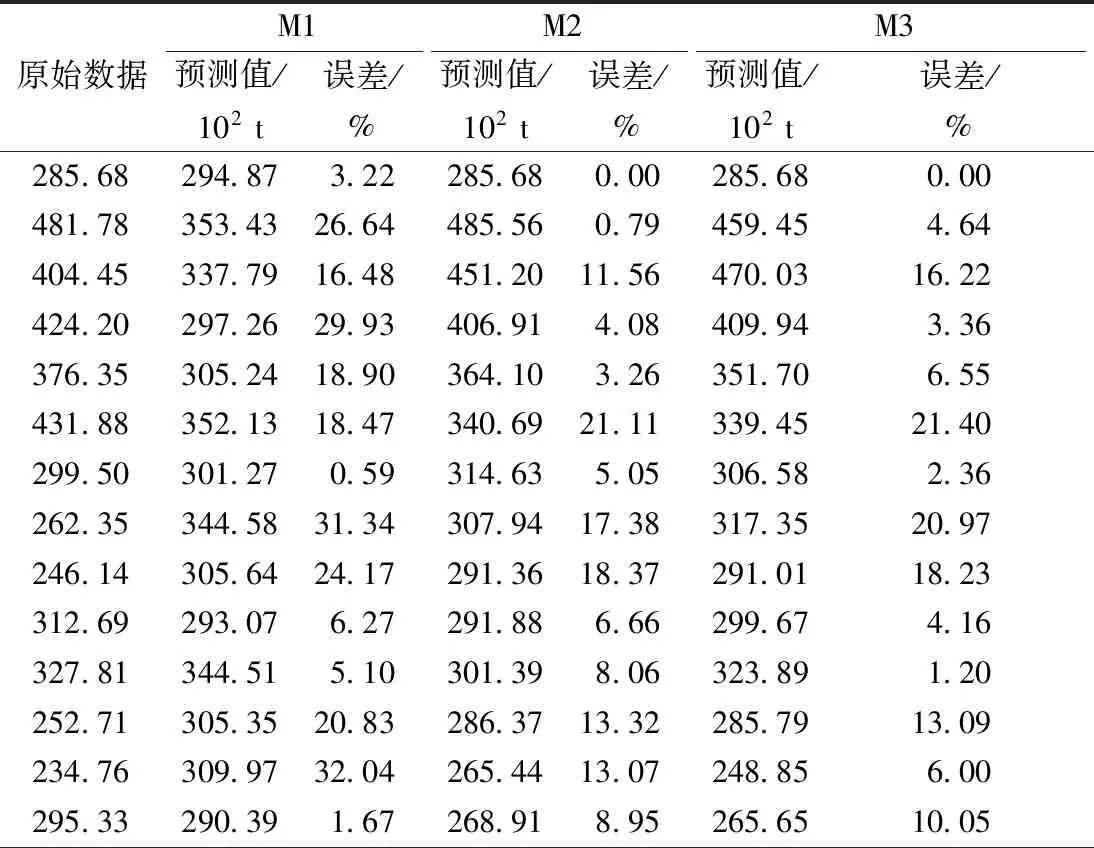
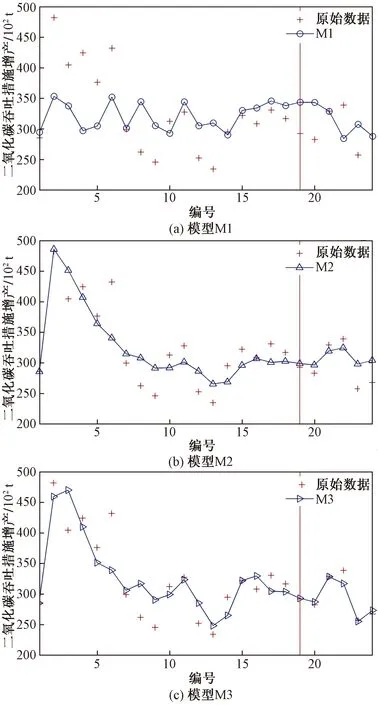
3 模型应用及结果分析





4 结论
