基于遗传算法的最小二乘支持向量机预测凝析气藏露点压力

汪 斌,孙博文,黄召庭,郭 平*,姚 琨,汪周华,白 银

(1.中国石油塔里木油田分公司勘探开发研究院，库尔勒 841000；2.西南石油大学油气藏地质及开发工程国家重点实验室，成都 610500)

在凝析气藏衰竭开发过程中，随着温度、压力的降低，当压力低于第一露点时，原本在凝析气中以气态存在的凝析油将逐渐析出，产生的反凝析现象不仅将凝析油损失在地层中，而且会堵塞地层渗流通道，降低气井产能[1-3]。为防止反凝析现象的产生，开采时常常保持地层压力高于上露点压力[4]。为此，准确测定凝析气藏露点压力，对于保障此类气藏高效开发至关重要。

目前，中国外确定凝析气藏露点压力的方法主要有：实验法、经验公式法、状态方程法等。实验法通常采用恒质膨胀(CCE)或定容衰竭(CVD)方法测定露点压力[5]，实验测试成本较高、耗时耗力；Nemeth等[6]基于多变量回归，提出了关于流体摩尔组成、气藏温度、C7+分子量、C7+相对密度的露点压力关联式，但经验模型普适性相对较差，泛化能力较弱；Elsharkawy等[7]提出了采用Soave R K(SRK)状态方程和Peng-Robinson(PR)状态方程进行凝析气藏露点压力计算，并对比了两个模型的预测精度，但热力学模型需要进行各组分的二元系数拟合，且求解收敛性存在一定的问题；随着人工智能技术的发展，如误差反向传播(BP)和径向基函数(RBF)等人工神经网络和基因表达式编程(GEP)等已成功运用于凝析气藏露点压力预测，胡世强等[8]利用BP神经网络预测了凝析气藏露点压力，Najafi-Marghmaleki等[9]将遗传算法(GA)和RBF结合，建立了GA-RBF露点压力预测模型，并同其他模型进行了精度对比，人工神经网络虽能进行复杂的非线性回归，但其调参工作量较大；Ahmadi等[10]基于GEP提出了一种简便、智能，能够更加准确地预测露点压力的模型。

为此，采用GA算法和最小二乘支持向量机(LSSVM)相结合的方法建立了一种基于机器学习的凝析气藏露点压力预测模型(GA-LSSVM)，并与BP和RBF人工神经网络方法进行预测精度对比。在皮尔逊关联性分析的基础上，上述模型均选取气藏温度、(N2+CO2、C1、C2～C6、C7+)摩尔分数、C7+相对分子质量、C7+相对密度和气油比作为自变量，露点压力为因变量。采用公开发表的34组露点压力数据进行模型优化，然后对15组实测露点压力数据进行预测。

1 理论基础

1.1 LSSVM基本原理

LSSVM是一种新型机器学习算法[11]，其在传统支持向量机SVM基础上，将二次规划问题中的不等式约束改为等式约束，极大地方便了求解过程，克服了数据集粗糙、数据集波动性大等问题造成的异常回归，能有效避免BP神经网络等方法中出现的局部最优等问题。

LSSVM回归的基本思想是通过一个非线性映射将低维空间的非线性回归问题转为高维特征空间的线性回归问题，给定一个训练集(xi,yi)(i=1,2,…,l)，LSSVM的回归函数为

f(x)=[ω,φ(x)]+b

(1)

式(1)中：ω是权向量；φ(x)是从输入空间到高维特征空间的非线性映；b是一个偏量。

根据结构风险最小化原则，LSSVM的优化目标可表示为

(2)

引入Lagrange乘子αi，则式(2)对偶问题的Lagrange多项式为

(3)

将式(3)代入Karush-Kuhn-Tucker条件可得：

(4)

从而求解的优化问题可以转化为求解式(5)中的线性方程组问题。

(5)

式(5)中：I=[1,2,…,l]T；α=[α1,α2,…,αl]T，b=[b1,b2,…,bl]T；y=[y1,y2,…,yl]T，A=ZZT+γ-1I，Z=[φ(x1),φ(x2),…,φ(xl)]T。

最终，LSSVM回归模型变为

(6)

式(6)中：K(xi,x)是LSSVM的核函数，常用径向基函数表述：

(7)

根据上述LSSVM原理，在给定样本以及核函数的条件下，LSSVM的性能主要受惩罚因子γ和核参数σ2的影响。因此，为获取参数γ和σ2的全局最优解，采用遗传算法进行参数优化。

1.2 GA算法

GA算法[12]是由美国密歇根大学的Holland于1975年提出的一种模拟生物进化论的自然选择和生物遗传的优化技术，是一种高度并行、自适应和全局性的概率搜索算法。GA求解问题的核心过程包括：编码(二进制)、遗传操作(选择、交叉、变异)、适应度函数。首先对优化参数进行二进制编码，将解空间转换成染色体空间；设定进化代数、个体长度、种群大小等初始群体参数；确定合适的适应度函数，计算群体中个体的适应度；然后对种群进行遗传算子操作，如选择、交叉和变异，经过迭代计算，使种群不断向最优方向进化，从而得到最优解[13]。由于LSSVM模型需要优化的参数有两个(惩罚因子γ，核参数σ2)，所以种群维数为2，GA其他设定参数如表1所示。

表1 GA算法初始参数设定Table 1 Initial parameter setting of GA algorithm

2 露点压力模型建立

GA-LSSVM、BP和RBF模型的程序编程均采用MATLAB 2016a软件，GA-LSSVM模型的建立需要结合LSSVM工具箱，将LSSVM算法嵌入GA算法进行扩展编程。根据设定的步长依次迭代，获取最优模型参数，然后在此基础上，完成模型的预测工作。

2.1 数据与变量选择

选取已公开发表的34组凝析气藏露点压力实验数据[14]分别对GA-LSSVM、BP和RBF模型进行参数优化，模型训练数据如表2所示。

表2 凝析气藏露点压力实验数据Table 2 Experimental data of dew point pressure in condensate gas reservoirs

续表2

由于实验数据级差较大，为加速模型训练速度，对所有数据采用归一化函数进行预处理：

(8)

式(8)中：x为变量的值；xmin为该变量中的最小值；xmax为该变量中的最大值。

在GA-LSSVM露点压力模型输入变量的选择问题上，利用IBM SPSS Statistics 23分析软件，采用皮尔逊(Pearson)双变量分析法，探究了各自变量对露点压力的影响排序(图1)。

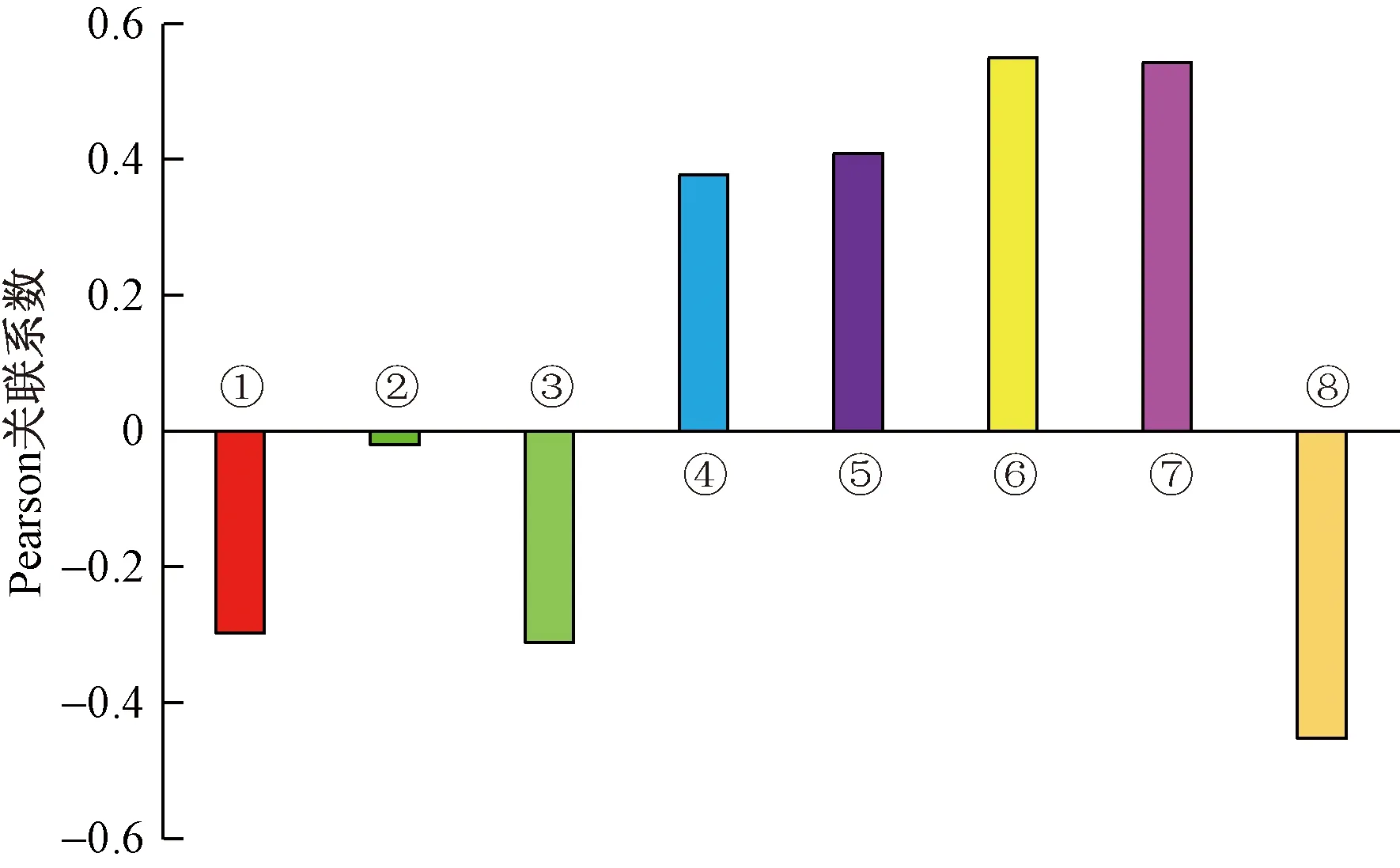
①为气藏温度；②、③、④、⑤分别为NO2+CO2、C1、C2～C6、C7摩尔分数；⑥、⑦分别为C7+相对分子质量和相对密度；⑧为油气比图1 露点压力影响因素分析Fig.1 Affecting factors analysis of dew point pressure

由图1可知，C2～C6、C7+摩尔分数、C7+相对分子质量、C7+相对密度与露点压力为正相关，其余变量为负相关。从分析可知，由于N2+CO2为非烃组分，且在凝析气中含量较低，对露点压力的影响程度较小。虽然凝析气流体的主要成分为甲烷，但“+”组分性质(摩尔组成、相对分子质量和相对密度)对露点压力有很大影响。为了更全面地考虑自变量对露点压力的影响，将选取气藏温度、(N2+CO2、C1、C2～C6、C7+)摩尔分数、C7+相对分子质量、C7+相对密度和气油比，8个变量作为GA-LSSVM模型的输入变量，露点压力为输出变量。其中：气藏温度为353.75～412.05 K，(N2+CO2、C1、C2～C6、C7+)摩尔分数分别为1.03%～14.96%、68.55%～94.55%、1.17%～24.87%、0.59%～9.84%，C7+相对分子质量为120～274，C7+相对密度为0.709～0.83，气油比为848～46 023 m3/m3。

2.2 模型参数优化

首先，定义绝对相对误差(ARD)和平均绝对相对误差(AARD)：

(9)

(10)

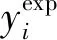
由于BP和RBF为较成熟的人工神经网络模型，具体的参数优化步骤此处不再赘述。GA-LSSVM露点压力预测模型的流程图如图2所示，优化后所有模型的最优参数如表3所示。

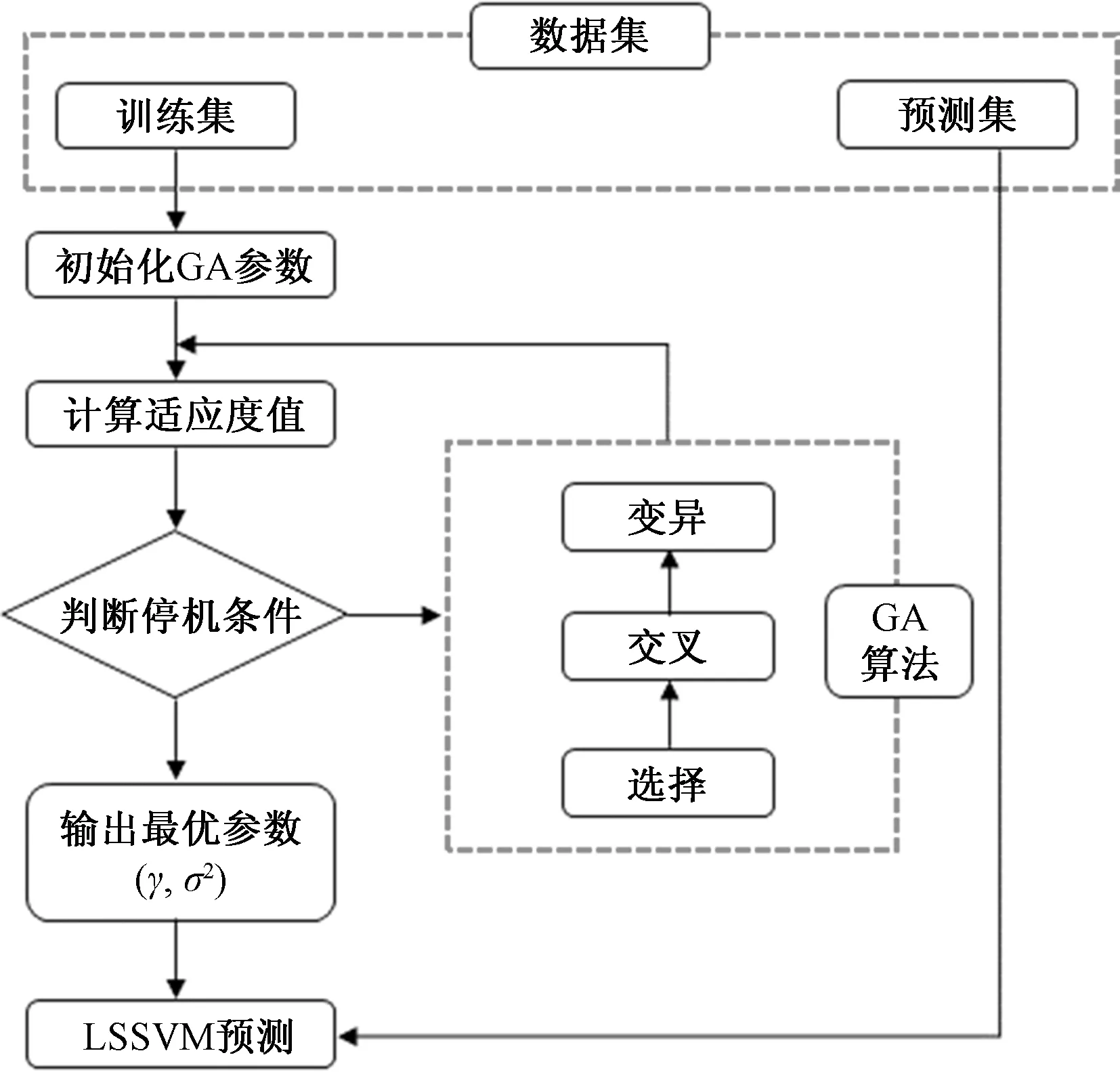
图2 GA-LSSVM模型计算流程图Fig.2 Flow chart of GA-LSSVM model

表3 各模型最优参数Table 3 Optimal parameters of each model

GA-LSSVM模型求解步骤如下：①将模型训练数据进行归一化处理，设定LSSVM参数范围和算法参数；②设置目标函数为AARD，初始化GA基本参数，优化LSSVM模型的两参数(γ，σ2)；③计算适应度函数，进行全局最优解判断，如果满足精度条件，则确定最优参数，反之进行选择，交叉，变异，重新迭代计算；④采用优化出的(γ，σ2)参数重启LSSVM模型，对非样本实验数据进行预测。

3 结果与分析

如图3所示，GA-LSSVM模型训练数据的预测值和实验值均匀分布在45°线附近，训练数据的AARD仅为1.78%，其中最小、最大ARD分别为0.05%和6.93，训练效果较好。BP和RBF模型的训练数据AARD分别为8.76%和6.10%，最大ARD均超过了20%，其中BP模型的最大ARD为80.78%，说明BP模型对个别数据的逼近能力较差。结果表明：建立GA-LSSVM模型对解决高度非线性的凝析气藏露点压力问题有良好的逼近能力，相对传统的BP和RBF模型有较大提升。

为了进一步表明本文建立的GA-LSSVM露点压力模型的预测性能，并与BP和RBF神经网络模型进行对比，选取除模型训练数据外的15组实测凝析气藏露点压力数据[14]进行预测，对比结果见表4。如图4所示，GA-LSSVM模型和RBF模型预测精度明显高于BP神经网络模型，两者预测数据AARD分别为5.84%和7.29%，最大ARD均低于17%，GA-LSSVM模型和RBF模型的预测值与实验值基本吻合，证实了该算法具有较好的露点压力预测精度。BP神经网络模型的预测AARD为14.21%，其中最大ARD为40.64%，预测效果相对较差。

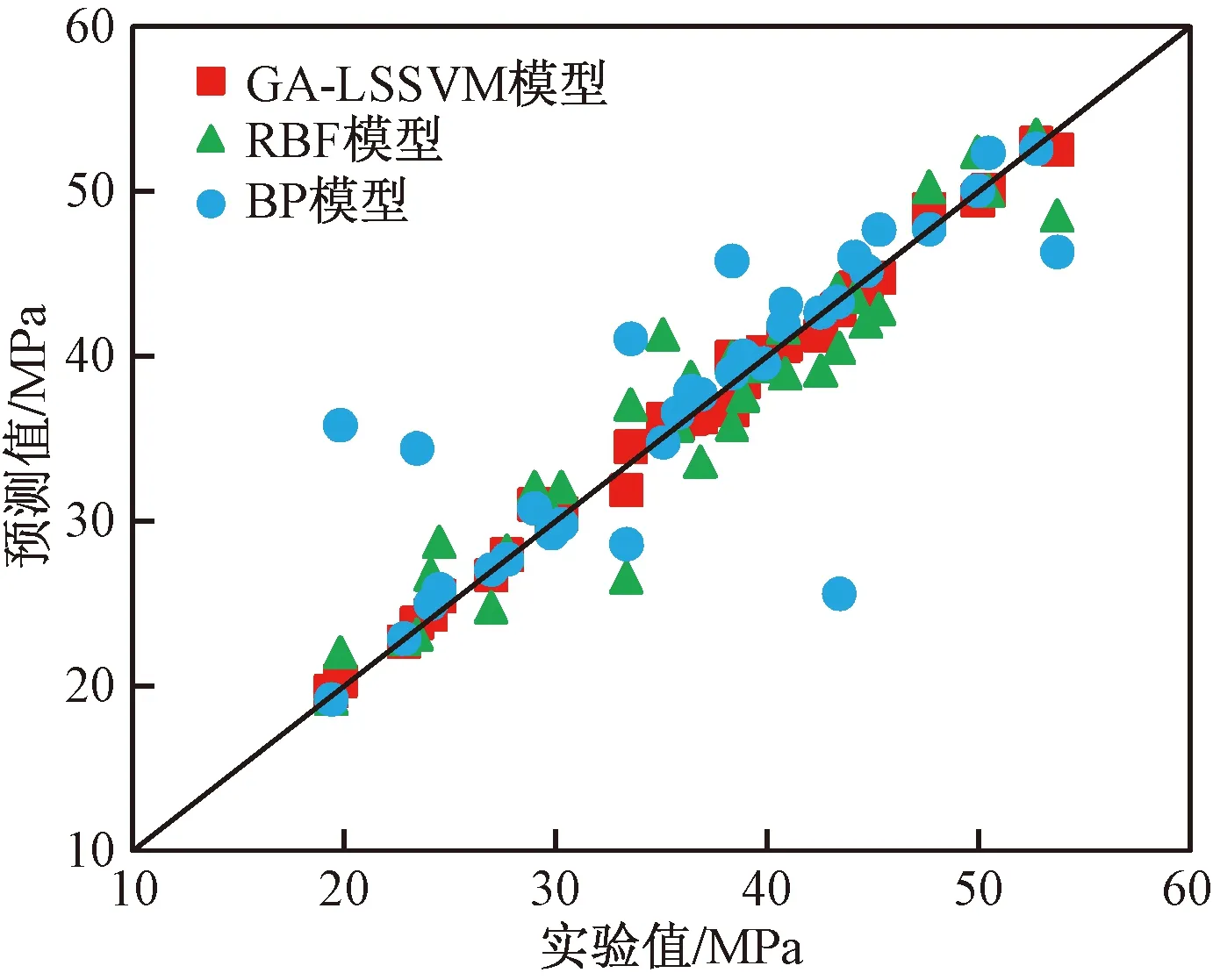
图3 各模型训练数据预测结果Fig.3 Prediction results of training data of each model

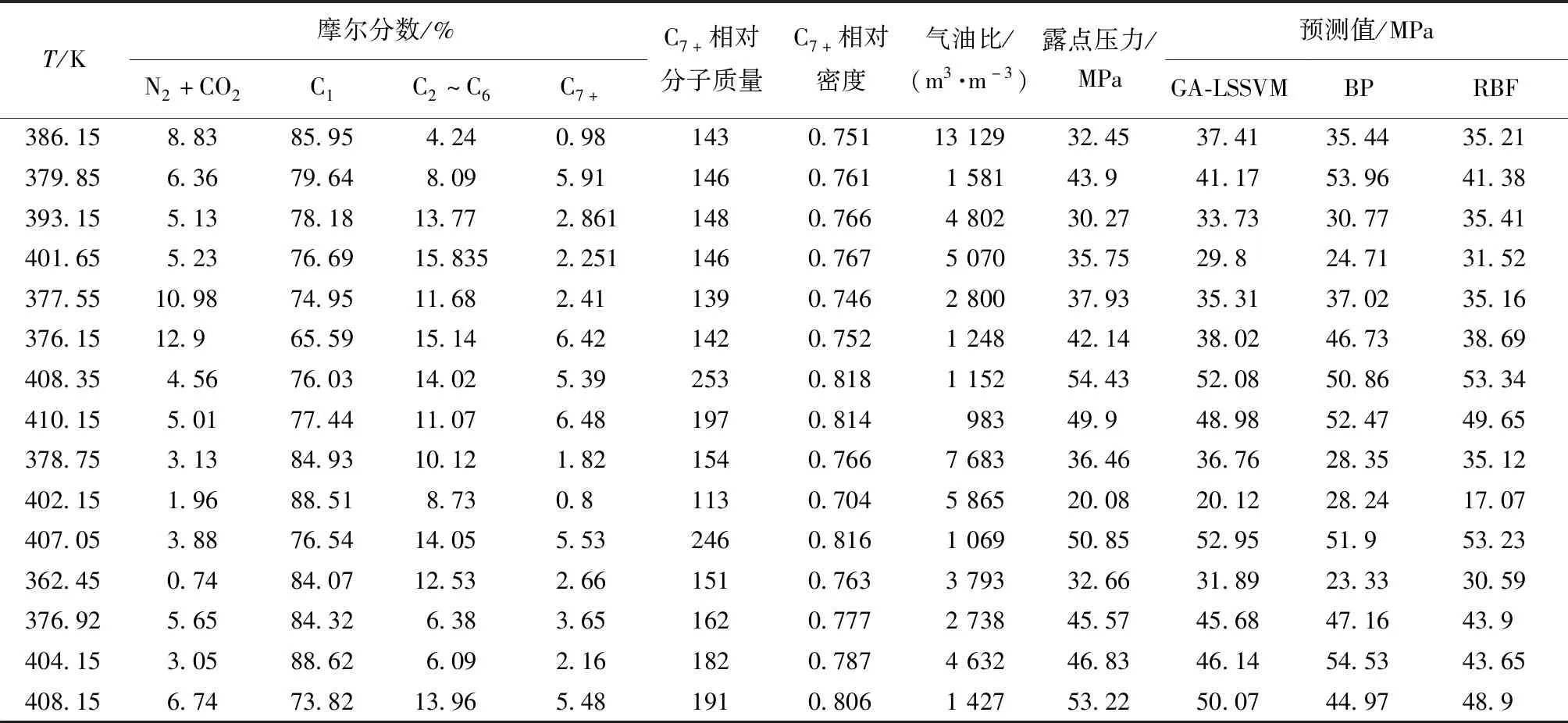
表4 各模型测试数据预测结果对比Table 4 Comparison of predicted results of test data of each model

图4 各模型测试数据预测结果Fig.4 Prediction results of test data for each model

4 异常点检测

根据Leverage方法[15]，能够进行实验数据的异常点检测，同时也能识别预测模型的有效性和适用范围，具体计算方法可参考文献[15]。

帽子矩阵(H)定义为

H=X(XTX)-1XT

(11)

式(11)中：X为二维列矩阵，矩阵行数取决于数据点个数，矩阵第二列为变量个数。

临界帽子值(H*)定义为

H*=3(p+1)/n

(12)

式(12)中：p为自变量个数；n为数据点个数。

标准残差(SR)定义为

(13)

通过上述方法，计算出模型对应的H、H*和SR，分别以H、SR为横纵坐标作出Leverage图。首先，如果数据点位于0≤H≤H*，-3≤SR≤3范围内，则说明模型对该数据有良好的预测能力；其次，若数据点位于H*≤H，-3≤SR≤3范围内，则说明该数据超出了模型的适用范围；最后，若数据点SR≤-3或SR≥3(无论H是否小于H*)，则定义为异常点，该数据实验值的正确性有待商榷。

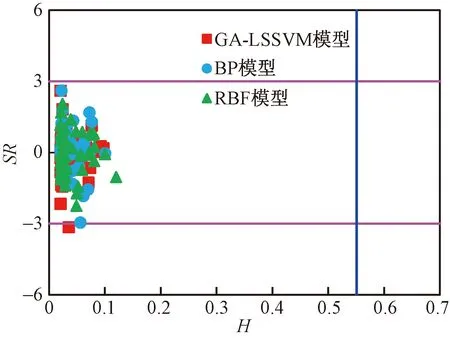
图5 Leverage方法异常点检测图Fig.5 Leverage method outlier detection map

如图5所示，仅有1个数据点的标准残差SR小于-3，界定为异常点。该数据点为测试数据中实验值为35.75 MPa的露点压力，通过分析可知，各模型对该数据点的预测误差均较大，GA-LSSVM、BP和RBF模型的预测ARD分别为16.61%、30.88%和11.83%。综上所述，该点实验值的正确性有待进一步验证，其余所有数据全部介于0≤H≤H*，-3≤SR≤3范围内。

5 结论

(1)将GA和LSSVM结合，运用MATLAB进行编程，建立了一种预测凝析气藏露点压力的新模型(GA-LSSVM模型)，同时根据BP和RBF人工神经网络方法，建立了相应的露点压力预测模型。

(2)运用IBM SPSS Statistics 23软件，采用Pearson双变量关联性分析，探究露点压力主力影响因素。最终确定模型的输入变量为：气藏温度、(N2+CO2、C1、C2～C6、C7+)摩尔分数、C7+相对分子质量、C7+相对密度和气油比。

(3)与BP和RBF模型相比，提出的GA-LSSVM模型AARD仅为2.59%，训练集和测试集的AARD分别为1.78%、5.84%，所有数据AARD为3.02%，精度相对较高，可满足凝析气藏工程计算的需要。模型适用范围如下，气藏温度为353.75～412.05 K、(N2+CO2、C1、C2～C6、C7+)摩尔分数分别为1.03%～14.96%、68.55%～94.55%、1.17%～24.87%、0.59%～9.84%，C7+相对分子质量为120～274，C7+相对密度为0.709～0.83，气油比为848～46 023 m3/m3。

(4)根据Leverage方法，对所有数据进行了异常点检测，仅有1个数据点为异常点，其余所有数据全部介于0≤H≤H*，-3≤SR≤3范围内。