利用蜂群算法优化的区域高程拟合精度分析

周 飞,张 炎,唐诗华,邢鹏威 ,张 跃

(1.广西壮族自治区基础地理信息中心，南宁 530023；2.桂林理工大学测绘地理信息学院，桂林 541006；3.广西空间信息与测绘重点实验室，桂林 541006)

随着现代测量技术的快速发展，全球定位技术(global positioning system，GPS)在测绘工作中的应用得以广泛推广，但GPS直接测定的是大地高，而实际工程中常用到的是正常高，两者之前存在一个高程异常值，因此如何获取高精度的高程异常值是GPS测量工作有待解决的问题[1]。目前常将粒子群算法、遗传算法、人工神经网络等智能算法应用于GPS高程拟合模型的构建，近一步提高了待求高程异常值的精度。蒲伦等[2]提出了利用粒子群算法对传统多面函数拟合方法进行优化处理，近一步提高了多面函数中特征值的搜索效率，为拟合模型的构建提供了合理的必要拟合参数。刘斌等[3]利用“移去-拟合-恢复”的思想，引出了基于EGM2008模型，并考虑地形因素影响的二次曲面拟合GPS高程的方法，模型的精度得到提高。刘建等[4]提出采用遗传算法优化径向基(radial basis function,RBF)神经网络来达到全局搜索最佳径向基函数中心值的目的，使得拟合模型能够更好地预测高程。最小二乘支持向量机(least squares support vector machine,LSSVM)利用少量的数据样本可以达到较好的高程拟合效果，关键之处在于最小二乘支持向量机中的正则化参数c和核参数σ，常规LSSVM拟合法中参数的优化常选用交叉验证法，但其存在计算量大且耗时长的缺陷，往往难以选定最佳参数值，拟合模型精度也难以达到期望值。寻求合适的方法提取最佳的参数值可以使拟合模型的精度得到进一步提升[5-6]。

相比其他智能算法，人工蜂群算法(artificial bee colony,ABC)具备参数少、计算简洁、可全局搜索最优值的特性[7]，现提出利用人工蜂群算法来优化最小二乘支持向量机的GPS高程拟合方法，利用人工蜂群算法能够快速广泛有效的寻求最优值的优势，为最小二乘支持向量机在规定的范围内找出最佳参数值，最终利用少量GPS水准重合点来构建GPS高程拟合模型。

1 基本理论

1.1 人工蜂群算法

人工蜂群优化算法是一种模仿蜜蜂寻找蜜源过程的生物智能优化算法。一个蜂群中根据群内工作的不同常常分为引领蜂、随行蜂、侦查蜂三种类型，其中引领蜂的工作是将发现的食物源的信息传递和分享给其他在蜂穴中等待的伙伴，所传的信息包括蜜源的方向、距离及存在的概率，随行蜂在接收到引领蜂传递的消息后，尝试寻找蜜源的具体位置，侦查蜂是寻找新的蜜源[8-9]。在蜜源搜寻工作中，引领蜂和随行蜂各占蜂群的一半，其整个过程可以被理解为求取目标函数最优值的过程。具体原理如下：

ABC首先要随机产生类似于蜜源最佳位置的初始值xi(i=1,2,…,N),且N为蜂群蜜蜂的数量，待求解的空间大小与xi的范围一致，蜜源的初始位置可以表示为

xi=md+rand(0,1) (md+Md)

(1)

式(1)中：md表示搜索范围的最小边界值；Md表示搜索范围的最大边界值；蜜源初始值随机分布在(md,Md)的范围内。引领蜂在初始蜜源的周围寻找新的蜜源Xj(j=1,2,…,N)，且新的蜜源位置不等于初始蜜源位置，可表示为

Xi=xi+φ(xi-xj)

(2)

式(2)中：φ是一个分布在[-1,1]之间的随机数，利用贪婪算法来评价两个蜜源的适应度fit，决定进行更新或保留原先蜜源：

(3)

式(3)中：fi为目标函数值，进一步需要计算随行蜂跟从引领蜂寻找蜜源的概率：

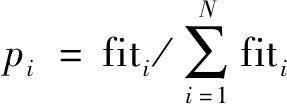
(4)

随行蜂的加入进一步缩小搜索的范围，并且每个随行蜂根据在[0,1]内产生的一个随机数α来决定是否跟随引领蜂，当pi>α时，随行蜂才会按照式(2)产生一个新蜜源，通过贪婪算法来决定应保留的蜜源，在经过有限的迭代次数后若仍未找到更优蜜源，则化为侦查蜂，根据式(1)寻求新的蜜源，若未放弃，则做出判断并保留最佳值。

1.2 最小二乘支持向量机

最小二乘支持向量机是由Suykens在原有支持向量机的基础上提出的，支持向量机具有结构简单、全局优化、泛化能力较好等特性，而LSSVM在同时具备这些优点之下还提高了收敛速度、化简了计算过程[10-11]。其具体步骤如下。

针对给定的训练集：

A={(x1,y1),(x2,y2),…,(xl,yl)}∈(Rn×Y)l

(5)

式(5)中：xi∈Rn，yi∈Y=R,i=1,2，…,l,利用非线性映射将样本输入映射到高维特征空间，构造出高维特征空间的线性回归函数：

g(x,w)=wTφ(x)+b

(6)

式(6)中：w为权值向量；b为阈值。根据结构风险最小化原理，将其转化为以下优化问题：

s.t.yi=wTφ(xi)+b+ξi

(7)

式(7)中：c为正则化参数；ξ为误差项；利用Lagrange函数和KKT(karush-kuhn-tucker)优化条件可以求得LSSVM的函数模型：

Z(x)=ai[φ(xk)φ(xi)]+b

(8)

K(xk,xj)=[φ(xk)φ(xi)]

(9)

根据Hilbert-Schmidt原理，引入核函数[式(10)]，进而将高维空间的内积计算转换为原空间中的函数的计算，解决了高维特征空间的计算问题，即：

(10)

选用径向基核函数作为LSSVM的核函数，以满足GPS拟合建模需求，即：

(11)

从上面整个过程可以看出，利用最小二乘支持向量机构建拟合模型只需要确定核函数参数σ和正则化参数c，相比原先，计算过程简洁许多。

2 ABC优化LSSVM

与其他智能算法相比，人工蜂群算法在搜寻目标函数最佳值的过程中不易受到自身参数的影响，且能够进行全局性搜查，避免了陷入局部最优值的缺陷[12]。该算法为最小二乘支持向量机选择最佳参数值，建立较高精度GPS高程拟合模型。ABC-LSSVM组合法的具体步骤如下：

(1)对收集的高程拟合数据进行归一化处理。

(2)ABC算法参数初始化：蜂群规模N，蜜源数量N/2，蜜源连续没被更新次数限值limit，最大迭代次数max,待优化参数个数D，参数的搜寻区间。

(3)确定初始值：在有效的范围内随机设置初始值，并计算出每个初始值所对应的LSSVM预测的均方根误差(RMSE),将其作为目标函数。

(4)寻找新的蜜源：引领蜂利用式(2)对每个蜜源寻找产生新的蜜xi，并保证选择的相邻蜜源不是当前蜜源及未超出范围，计算变异后的蜜源的目标函数值和适应函数值，与当前蜜源进行比较，判断当前蜜源是否需要进行更新，如果当前蜜源未更新的次数超过限制limit,则放弃该蜜源，寻找新的蜜源。

(5)再次开发新的蜜源：引领蜂将更新完的蜜源信息传递给随行蜂，随行蜂经过相应的概率比较来决定是否要对新的蜜源进行再次更新，若符合继续开发的条件，随行蜂进行再次开发的步骤同(4),并保留下最优蜜源(解)。

(6)迭代次数达到最大值max:当随行蜂的迭代次数达到最大值时，没有再找到新的更优蜜源，则随行蜂转化为侦查蜂，侦查蜂会通过式(1)产生新的蜜源。

(7)判断更新的蜜源是否满足条件，当新的蜜源(解)满足最终要求，则保留最优值，否则返回到(4)继续寻找。

(8)LSSVM构建GPS高程拟合模型：利用ABC优化的最佳参数值，代入LSSVM中建立高程拟合模型，并通过检测数据获取拟合模型的内外符合精度，进行比较分析。

经过多次迭代寻求最佳值的过程，ABC-LSSVM可以进行全局性的搜寻到最佳参数，进一步加快收敛的速度，最终获取最佳拟合模型。

3 实验分析

3.1 采集研究数据

为验证人工蜂群优化最小二乘支持向量机拟合方法在构建GPS高程拟合模型方面是否有效可行，同时与之前的方法构建的模型进行精度对比分析，选择了广西东北方向部分地方作为研究区，覆盖面积约在100 km2,地形条件较为复杂，山地略多，在研究区域内采集了41个GPS点数据，点之间相隔为1.5～2.5 km，并与水准进行了联测，点位精度均满足研究要求，为蜂群算法优化最小二乘支持向量机拟合法提供必要的基础数据条件。在采集的41个GPS水准重合点中选择出31个分布均匀的点用来构建模型，剩余的10个GPS水准重合点用来检验人工蜂群优化后的拟合模型精度，点位分布如图1所示。分别利用优化后的最小二乘支持向量机拟合法与其他两种方法在同一批GPS水准重合点基础上建立拟合模型，并对拟合结果进行对比分析。

图1 测区点位分布Fig.1 Distribution of points in the survey area

3.2 拟合模型精度分析

在利用人工蜂群算法优化最小二乘支持向量机拟合法构建模型时，需要对初始值及迭代次数进行设置，将蜂群种群规模设置为20，蜜源连续没被更新次数限值设置为100，最大迭代次数为80。由于LSSVM在进行拟合模型的构建时需要优化的参数只有正则化参数c和核参数σ，因此待解问题的维数D=2，取值范围均为(0.01,50),最后将拟合的结果与BP神经网络拟合法、常规LSSVM拟合法的结果进行对比分析。为初步验证拟合模型的稳定及有效性，分别利用3种不同拟合方法进行了多次试验，如表1所示为10次实验中模型的内符合精度。

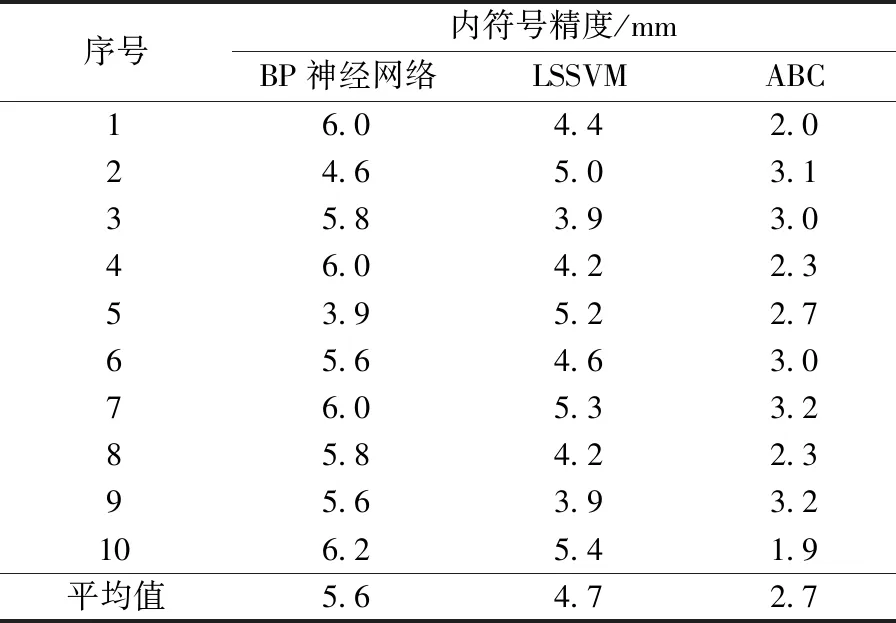
表1 三种拟合方法的内符合精度比较Table 1 Comparison of internal accuracy of three fitting methods

根据表1统计可知，在10次的实验中，人工蜂群优化后建立的模型内符合精度均值为2.7 mm,常规LSSVM构建模型均值为4.7 mm,BP神经网络拟合法为5.6 mm,无论是均值还是10次实验中内符合精度的波动范围，ABC-LSSVM组合拟合法构建的模型均优于其他两种方法，且稳定性更为理想。

为了更加详细的对比分析3种方法的拟合效果，利用三种方法建立的拟合模型，获取了10个拟合检测点的高程异常值，并对检测点的拟合残差进行对比分析(表2)。

从表2可以看出，ABC-LSSVM组合法的检核点残差平均值及残差平方均值均要小于其他两种方法，经过对实验数据分析可以看出该方法的拟合结果的变化范围较小，拟合精度较高；而BP神经网络拟合法的变化范围最大，拟合精度最为不稳定，在用来建立GPS高程拟合模型时难以达到理想的精度；为了更近一步直观地显示ABC-LSSVM拟合法的有效可行性，绘制了10个检核点的残差变化对比图(图2)。

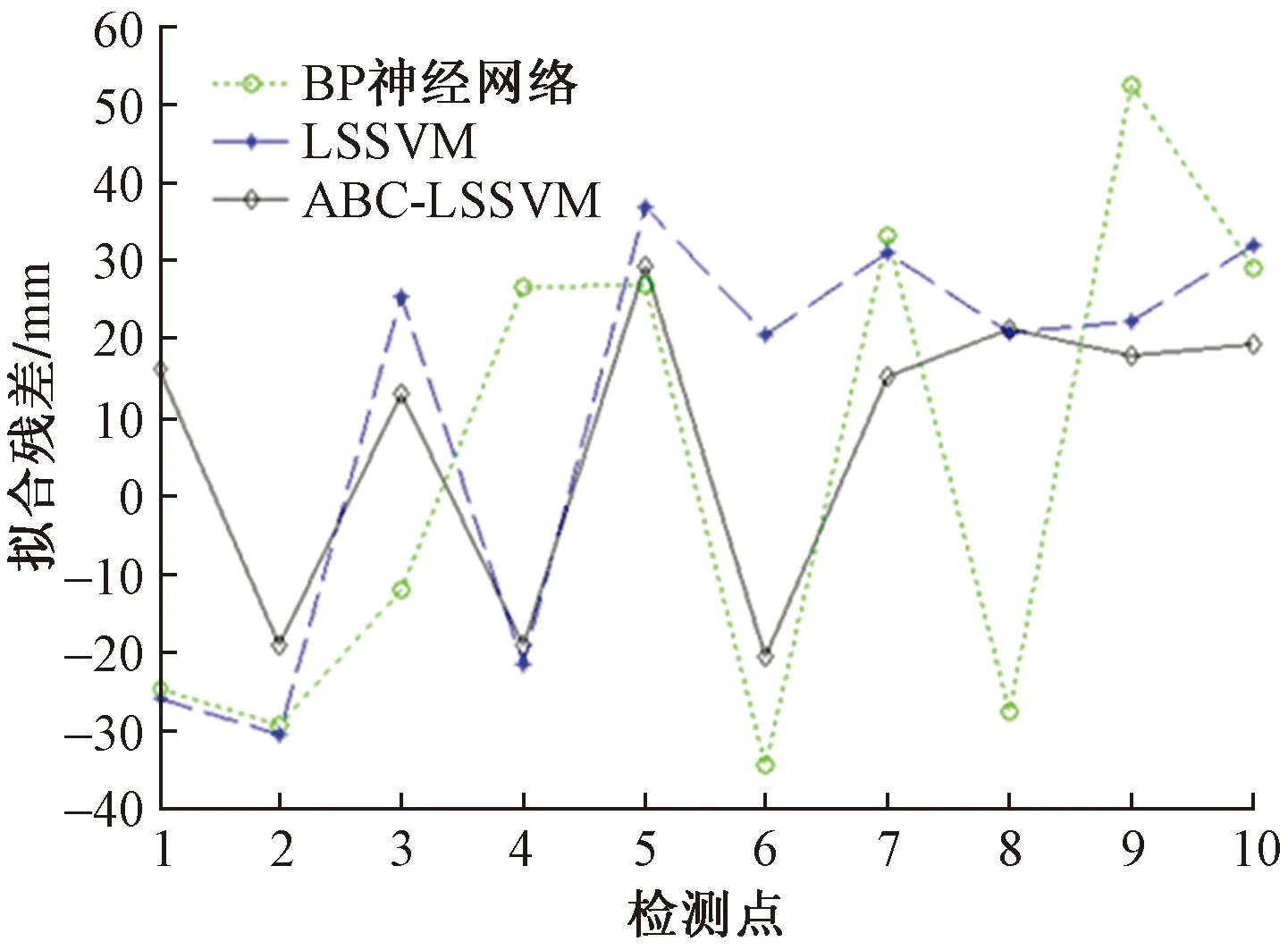
图2 三种拟合方法的残差对比Fig.2 Residual comparison of three fitting methods

图2直观形象地展示了人工蜂群优化拟合法比常规最小二乘支持向量机拟合法更好。根据检测点的残差走势图可以看出，BP神经网络拟合法的残差数值波动最大，常规LSSVM的波动略低于BP神经网络，但相比与蜂群优化法，其后5个检核点的残差值均高于蜂群优化法，整体的波动范围远也大于蜂群优化法，从总体精度上讲，人工蜂群优化拟合法的模型精度最佳，能够充分的表示出实际地形特征，构建的拟合模型精度也有所提高。

为增强10个检核点的精度评定结果的可信度，更加形象地展示模型的精度，分别利用3种方法进行多次试验，统计了15次实验中检核点的外符合精度及均值，通过所有实验的平均值与单次的测量值进行比较分析，获取最为合理的GPS拟合模型的精度，最终的测试结果如表3所示。

表2 检测点的拟合残差对比Table 2 Comparison of fitting residuals of detection points

根据表3中的数据可看出，无论是每次实验的外符合精度还是15次实验后的精度均值，人工蜂群改进的拟合法均要优于其他两种方法，经计算后蜂群改进的拟合法构建的拟合模型平均精度为±19.8 mm,在选用相同的一组测试数据的基础上，常规的LSSVM拟合法的拟合精度为±27.5 mm，蜂群优化法的精度比其提高了28%，与BP神经网络拟合方法相比，人工蜂群优化最小二乘支持向量机拟合法构建模型的精度提高了36.1%，充分说明了人工蜂群优化拟合法可以提高GPS拟合模型的精度。

表3 不同方法的检测精度比较Table 3 Comparison of detection accuracy of different methods

4 结论

为了解决最小二乘支持机拟合方法建立GPS高程拟合模型时参数选择较为困难的问题，提出利用人工蜂群算法对最小二乘支持向量机拟合法进行参数优化，并通过实验与其他方法进行了对比分析，得出如下结论。

(1)在人工蜂群优化算法中，设置随机初始值及迭代次数最大值，选定参数固定范围，通过不同的分工来增加生物的多样性，确保最终的获取结果为全局最优，避免陷入局部最优解的麻烦，寻优过程中工作性质的不断转换提高了收敛速度，短时间内为最小二乘支持向量机构建拟合模型提供了最佳的拟合参数。

(2)常规最小二乘支持向量机拟合法常通过交叉验证法寻求拟合模型参数，而本次利用人工蜂群算法进行参数寻优，多次实验内外符合精度统计及残差走势图均表明人工蜂群算法优化拟合法的收敛效果更佳，在有效的搜索范围内，更加有利于搜索最优值的效率。

(3)根据实验结果可知，相比其他两种方法，蜂群优化拟合法的建模精度较高。其拟合模型的总体精度为±19.8 mm,比常规最小二乘支持向量机拟合法提高了28%，比BP神经网络拟合法提高了36.1%，充分证明了人工蜂群优化拟合法的有效可行性。

提出的蜂群优化最小二乘支持向量机拟合法在建立模型中是否有效可行得到了充分的验证，但是实验区域范围有限，针对较大范围的拟合区域，该方法构建拟合模型的稳定性和有效性需要进一步验证。