全电直驱集成动力系统扭振固有特性灵敏度分析及动力学设计

李孝磊， 葛文庆， 汪学杞， 马驰骋， 谭 草， 李 波

(山东理工大学交通与车辆工程学院，淄博 255000)

电动汽车平顺性是评价整车性能优劣的重要衡量指标，而动力传动系统的扭转振动是影响电动汽车平顺性的关键因素。改善动力传动系统的平顺性是提升电动汽车平顺性的有效途径之一[1]。

准确分析集成动力传动系统的扭振固有特性是提升集成动力传动系统平顺性的必要一步，而建立有效的模型是保证固有特性分析结果准确的前提，为此建立有效的固有特性力学分支模型显得格外重要。文献[2-3]综合考虑电磁刚度与不考虑电磁刚度时建立传动系统的集中-分布质量模型进行自由扭振分析，结果显示考虑电磁刚度时，更能充分反映汽车在低速下的丰富动力学现象。文献[4- 6]针对某混合动力汽车传动系统分别建立不同自由度的力学模型进行固有特性分析，结果表明建立详细模型能反映丰富的动力学现象。文献[7-8]考虑齿侧间隙的非线性因素建立了动力传动系统不同自由度模型，利用有限元法分析系统不同部件的固有频率和模态特性。

近年来，中外学者通过设计改进结构参数，达到减轻传动系统扭振的目的。文献[9]针对动力分流混合动力汽车优化双质量飞轮惯量，实现最小的振动响应参数组合，达到减振降噪目的。文献[10]针对并联混合动力汽车动力传动系扭振,利用多目标下坡单纯形优化算法对启动工况下5个设计变量进行优化，以期通过优化系统特征参数达到减小谐振的目的，并试验验证此方法的可靠性。文献[11-12]针对某型车基于灵敏度分析法分析系统转动惯量和扭转刚度对固有频率的灵敏度，并且进行了动力学参数的修改。文献[13]通过使用变参数的非线性能量吸振器改善传动系统的平顺性，而且通过寻取最优的非线性能量吸振器的参数，提升系统的平顺性。

提出一种新型双速全电直驱集成动力传动系统，由电机、双速电磁直驱变速器、减速器总成、车轮和车身组成的多自由度振动系统。文献[3- 8，14-15]所研究的电动车动力驱动系统皆为电机与变速器通过机械连接，实现动力的传递，而本文所提出的新型集成动力传动系统的电机轴与变速器输入轴同为一轴，实现无缝动力传递，结构更加紧凑，工程实现更容易。

针对机电耦合的动力传动系统建立综合考虑电磁刚度、齿轮时变啮合刚度等因素耦合作用的8自由度力学分支模型，分析系统的固有频率和振型，并利用Adams验证了固有特性分析结果的有效性；在此基础确定不同工况临界转速，并基于灵敏度分析法对固有频率进行分析，找出对固有频率最敏感的特征参数；进而有针对性地优化系统特征参数，实现将共振转速移出常用转速范围；同时针对系统参数优化前后仿真分析比较系统的动态变化。

1 全电直驱集成动力传动系统建模

1.1 系统结构与原理

双速全电直驱集成动力传动系统采用电机FF(front-motor，front-drive)的动力传动方式。电机与电磁直驱变速器、减/差速器总成高度集成，通过左右半轴和车轮传递动力驱动车辆行驶。全电直驱集成动力传动系统结构如图1所示。

图1 全电直驱集成动力传动系统示意图Fig.1 Schematic diagram of all-electric direct-drive integrated powertrain system

全电直驱集成动力传动系统的电磁直驱变速器是自主研发的高度集成变速系统，利用电-磁作动器产生换挡力，驱动接合套完成进退挡。与传统电动汽车不同点在于：①电机与变速器输入轴合为一体；②电-磁作动器产生换挡力；③电-磁作动器换挡响应速度更快，动力中断时间更短；④结构更加紧凑。其结构如图2所示。

图2 双速全电直驱集成动力系统Fig.2 Two-speed all-electric direct-drive integrated power system

1.2 固有特性分析模型的建立

根据图1所示新型全电直驱集成动力传动系统的示意图，综合考虑电机电磁刚度、齿轮时变啮合刚度等非线性因素，建立集成系统电机、变速器主/被动齿轮部分、主减速器主/被动齿轮部分、左/右车轮、车身8自由度的扭振非线性力学分支模型，如图3所示。

Jn为第n个构件当量转动惯量；为分别代表第n个构件的扭振角位移、角速度、角加速度；n分别代表m、tg1、tg2、rg1、rg2、lw、rw、b，依次代表本节上述8个自由度的构件；K1～K6分别代表电机轴、输出轴、左/右半轴、左/右车轮当量扭转刚度；K12、K34为代表变速器和主减速器齿轮副综合啮合刚度图3 集成动力传动系统扭振力学模型Fig.3 Torsional vibration mechanical model of integrated powertrain system

为能更有效地分析系统的扭振固有特性，需要根据系统转换前后动能和势能大小不变的原则将系统简化为惯性元件和弹性元件，并进行归一化处理。针对图3所示的8自由度力学分支模型根据力学原理建立不同子系统的无阻尼扭振微分方程。

1.2.1 电机子系统模型

电机子系统除考虑转子转动惯量，电机轴的扭转刚度外，还将考虑电磁刚度的影响。电磁刚度，即为电磁转矩中电转角的一次项系数[16]。电磁转矩计算方程为

(1)

电磁刚度计算方程为

(2)

式中：P为磁极对数；θ为电转角；Ψf为永磁体磁链，Ld、Lq分别为d、q轴电感；id、iq分别为d、q轴电流。

不同工况下电机电磁转矩随直交轴电流变化关系如图4所示，进而求得电磁刚度。

电机子系统数学模型为

(3)

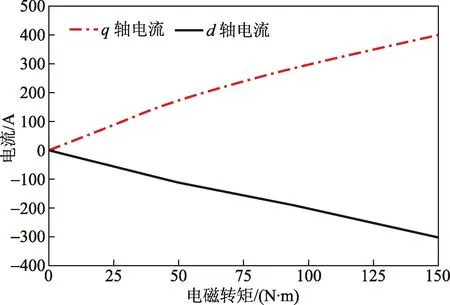
图4 直交轴电流与电磁转矩关系Fig.4 Relationship between rectangular axis current and electromagnetic torque

1.2.2 双速电磁直驱变速器子系统模型

根据电磁直驱变速器实际结构特征，将齿轮、轴和电-磁作动器部分按一定原则等效简化为主动齿轮部分和从动齿轮部分，并且进行归一化处理，力学模型如图5所示。

Ttg1、Ttg2为齿轮所受扭转力矩；C12为齿轮副啮合阻尼；e(t)为静态传递误差图5 啮合齿轮副力学模型Fig.5 Mechanical model of meshing gear pair

传动过程中，除考虑各元件的转动惯量和扭转刚度外，轮齿交替啮合时，导致齿轮啮合刚度随啮合相位改变而改变，其严重影响固有特性分析结果准确性。为此在ABAQUS中利用准静态有限元分析法定义三个增量步，分析齿轮时变啮合刚度，并与国际标准ISO 6336—2018[17]校验，结果如图6、图7所示。

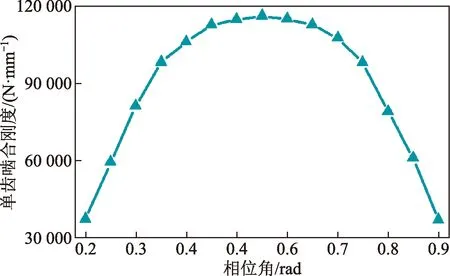
图6 单齿啮合刚度Fig.6 Mesh stiffness of single gear

图7 综合啮合刚度Fig.7 Comprehensive meshing stiffness

图6为啮合过程中单齿啮合刚度变化，根据经验公式推导出综合啮合刚度。由图7可以看出， 齿轮副传动过程中啮合齿轮单双齿交替啮合，导致其所承受的载荷呈周期性变化，使得综合啮合刚度呈周期性变化。

电磁直驱变速器主、从动部分振动微分方程如式(4)、式(5)所示。

K1(θtg1-θm)=0

(4)

K2(θtg2-θrg1)=0

(5)

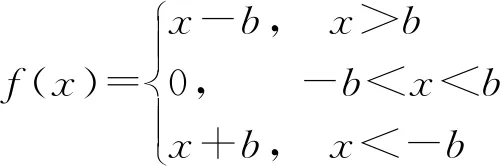
(6)

式中：f(x)为齿侧间隙非线性描述的函数；b为齿侧间隙[18]。

1.2.3 减速器子系统模型

同理，考虑减速器齿轮时变啮合刚度对固有特性的影响，将差速器转动惯量等效转化到主减速器部分。主减速器主从动部分振动微分方程：

K2(θrg1-θtg2)=0

(7)

K3(θrg2-θlw)+K4(θrg2-θrw)=0

(8)

1.2.4 左右车轮子系统模型

根据图3扭振力学模型,综合考虑左/右车轮部分转动惯量和扭转刚度,分别得到左/右车轮子系统的扭振微分方程:

(9)

(10)

1.2.5 车身子系统模型

根据图3扭振力学模型,将车身视为一子系统分析车身的模态特性,车身子系统的扭振微分方程:

(11)

集成动力传动系统扭振固有特性的数学模型如式(3)～式(11)，在MATLAB中编程求解系统固有频率和振型。

2 扭振固有特性分析

2.1 模型验证与结果分析

为验证扭振固有特性分析模型的有效性，在Adams中建立系统的虚拟样机，如图8所示，将 Adams 中提取的固有频率与解析法计算结果进行校对，校对结果表1所示[19-20]。

图8 双速全电直驱集成动力传动系统虚拟样机Fig.8 Virtual prototype of two-speed all-electric direct-drive integrated power powertrain system

通过表1比较看出相对误差在5.2%以内，进一步说明所建模型的准确性。在Adams中提取固有频率前去除电磁刚度约束，则不能获得“零阶”固有频率。充分说明考虑电磁刚度，可以获得更为低阶的固有频率，有利于分析“零阶”固有频率对系统的影响。

集成系统在不同挡位的8阶主振型如图9所示。横坐标1～8个惯性元件代表电机、变速器主/被动齿轮部分、主减速器主/被动齿轮部分、左/右车轮、车身。

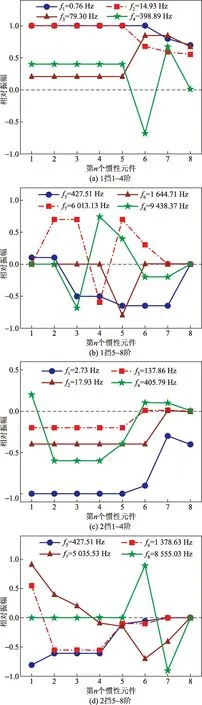
图9 1挡、2挡各阶主振型Fig.9 Main vibration mode of each order in gear 1 and gear 2

由图9(a)、图9(b)可以看出，1挡时1～4阶振动表现在主减速器、车轮、车身位置，其对应车速为低速状态。第四阶固有频率所对应的主振型中左右车轮出现相反方向的振动，且出现了节点，说明左右半轴所受扭转应力较大，容易出现危险点，进而可以为传感器的布置提供参考，5、6、8阶振动表现在变速器、主减速器部分，第五阶固有频率所对应的主振型波动幅值较大，且对变速器被动齿轮以及输出轴的影响较大，并且此频率对应的临界转速处于常用转速。

表1 集成系统固有频率Table 1 Natural frequency of integrated system

由图9(c)、图9(d)可以看出，2挡时1～4阶振动同样表现在主减速器、车轮、车身位置，其对应车速为低速状态。5、6阶振动表现在变速器及主减速器部分；7阶振动表现在主减速器部分。

2.2 电机临界转速

电机转矩的谐波转矩是集成动力系统扭转振动的主要激励源，当电机谐波转矩的频率与系统的固有频率接近时，就会产生共振。为准确掌握集成系统易发生共振的临界转速，根据式(12)分析1、2挡时集成系统临界转速。

(12)

式(12)中：n′为电机临界转速；f为集成系统扭振固有频率；r为电机谐波转矩的频次。在电机谐波转矩中，将考虑扭振波动幅值较明显的两低阶频次，即电频率的6倍与12倍，研究的永磁同步电机为4对极，由此确定了r的取值为24和48[21]。系统在不同阶次下1、2挡的临界转速如图10所示。

图10 1挡、2挡临界转速Fig.10 Critical speed in gear 1 and gear 2

从图10看出，在低频阶段容易发生共振现象，特别是共振转速处于常用转速范围时，需要引起足够重视。其中图10第五阶固有频率所对应的临界转速均为534、1 069 r/min，由模态分析结果看出，特别是1挡时变速器及主减速器部分共振幅值较大，应设法将此共振转速移出常用转速范围。

2.3 固有频率对惯量和刚度灵敏度分析

利用灵敏度分析法分析固有频率对转动惯量和扭转刚度的灵敏度，找出对固有频率影响最敏感的特征参数，对其有针对性修改，实现将共振转速移出常用转速范围。

图11 固有频率对转动惯量灵敏度扭转刚度灵敏度Fig.11 Sensitivity of natural frequency to moment of inertia and torsional stiffness

第k阶固有频率fk对第n个构件转动惯量Jn的灵敏度为

(13)

式(13)中：(θk)n为系统第k阶模态振型中第n个元素。

第k阶固有频率fk对第j个轴扭转刚度Kj的灵敏度为

(14)

式(14)中:(fk)j为集成系统第k阶固有频率中第j个轴段的扭转刚度。

首先，根据全电直驱集成系统的常用转速范围，由于重点研究对象为电磁直驱变速系统，确定针对1挡时第五阶固有频率进行灵敏度分析，由图10(a)看出此时的临界转速为1 069 r/min。根据式(13)、式(14)就第五阶固有频率对系统转动惯量和扭转刚度的灵敏度进行分析。

通过图11看出，影响第五阶固有频率的敏感参数为第3个转动惯量件和第3个轴段，分别对应变速器被动齿轮及其关联的部件Jtg3和变速器输出轴部分K2，从而确定了后续设计改进的对象。

3 结构参数的动力学设计与分析

3.1 基于灵敏度分析结果的动力学设计

从2.3节中看出：集成系统的Jtg3和K2对于第五阶固有频率的影响最为敏感。以Jtg3和K2为优化变量，以第五阶固有频率为目标函数进行优化。初步选定Jtg3和K2的变化范围为原始数据的±30%，编写MATLAB程序，分析得到第五阶固有频率随Jtg3和K2变化的曲面图，如图12所示。

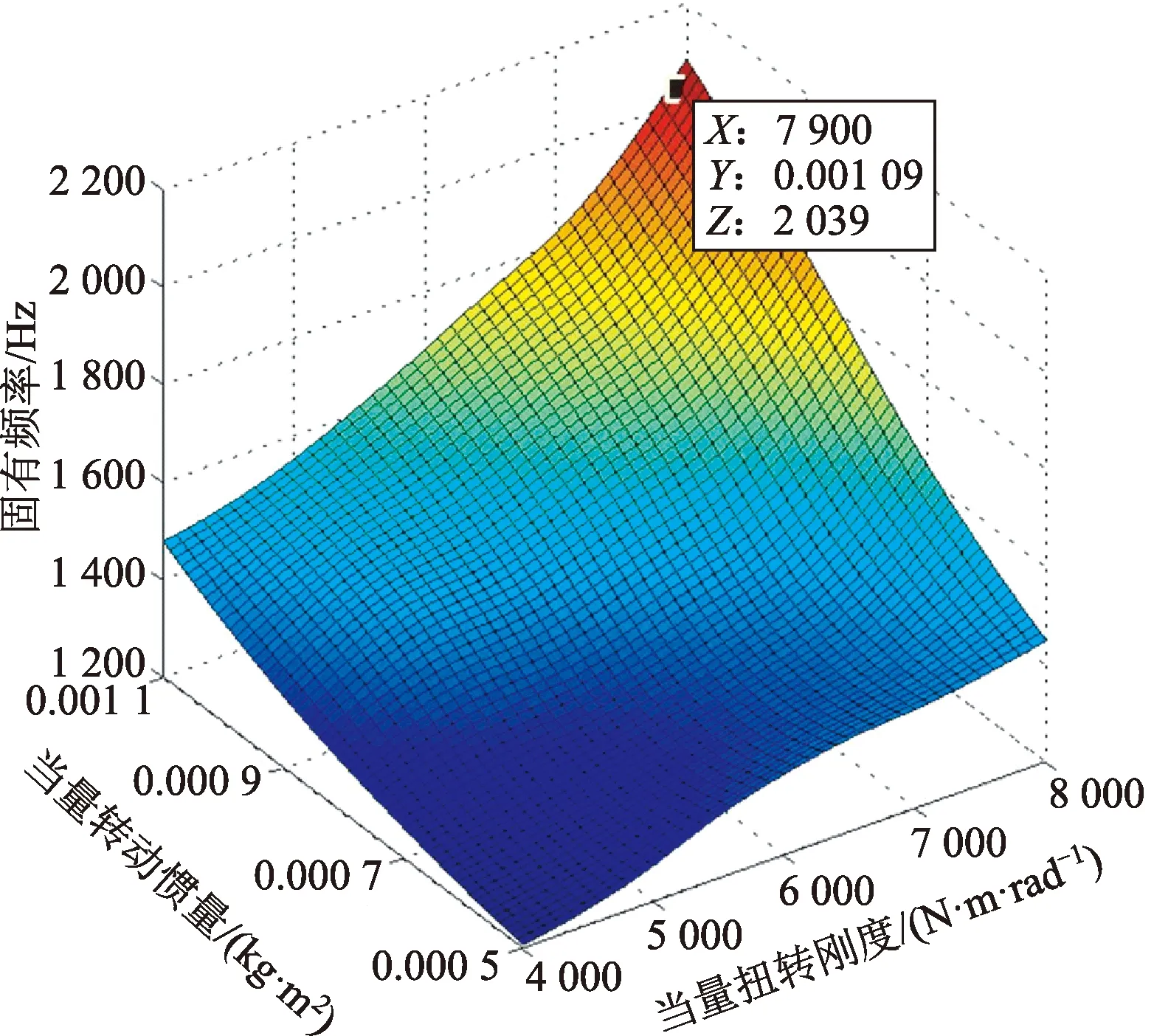
图12 固有频率优化后曲面图Fig.12 Surface diagram after natural frequency optimization

由图12可以看出，当集成动力传动系统的转动惯量为0.001 09 kg·m2，扭转刚度为7 900 N·m/rad时，固有频率为2 039 Hz，所对应临界转速为 5 097 r/min，远大于集成系统常用转速范围，达到了优化的目的，可进一步看出转动惯量的改变对固有频率的影响较小，而扭转刚度的改变对固有频率影响较大。

3.2 基于结构参数修改后的定量分析

将3.1节中修改后的结构参数赋值在Adams与SIMULINK的联合仿真模型中，验证电机临界转速为1 069 r/min变速器处于1挡时结构参数优化前后电机轴以及输出轴的动态变化。

由优化前后系统动态响应结果看出，当Jtg3为0.001 09 kg·m2、K2为7 900 N·m/rad时，电机轴角加速度频域响应由5.45 rad/s2减小为4.04 rad/s2，最大谐波幅值减小了25.9%，但新增供电电流2倍频(142.5 Hz)的激励幅值，幅值较小(图13)；变速器输出轴最大转速由813.98 r/min减小为 811.90 r/min，幅值减小了0.26%，由图14对比可得，系统整体波动明显减小，总体上看出结构参数优化后，系统平顺性明显得到提高。

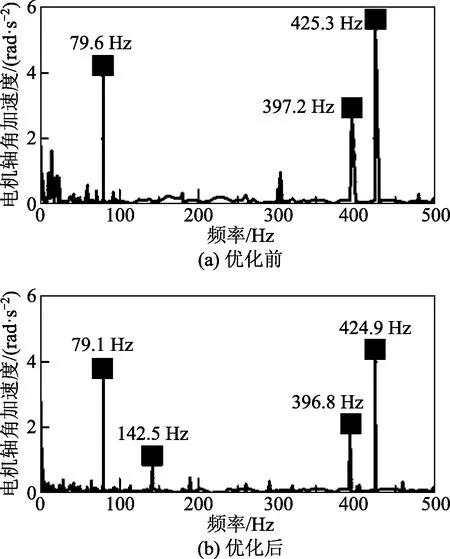
图13 电机轴角加速度Fig.13 Motor shaft angular acceleration

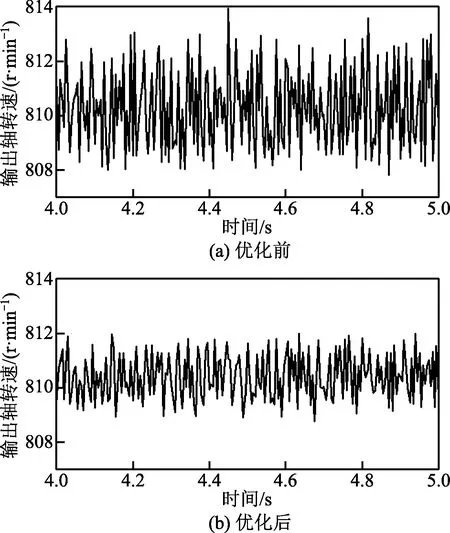
图14 输出轴转速Fig.14 Output shaft speed

4 结论

针对新型双速全电直驱集成动力传动系统建立了综合考虑电磁刚度、齿轮时变啮合刚度等非线性因素耦合作用的8自由度力学分支模型，计算和分析了系统的固有频率和振型；并利用Adams验证了固有频率的有效性，基于直接求导法对固有频率进行了灵敏度分析，根据灵敏度分析结果进行结构参数的优化，进而将优化后的系统进行了仿真分析。根据分析数据，得出如下结论。

(1)分析了全电直驱集成动力系统的扭振固有特性。考虑电磁刚度时得到“零阶”固有频率，动力学现象更为丰富。低阶固有频率主要对于车轮、车身影响较大，高阶固有频率对变速器的影响较大，对于车身、车轮的影响较小。高阶振动被变速系统过滤掉，使得车身波动较小。

(2)对固有频率进行了灵敏度分析，基于灵敏度分析结果进行了结构参数设计改进。当集成动力传动系统的转动惯量为0.001 09 kg·m2，扭转刚度为7 900 N·m/rad时，此时所对应的临界转速为5 097 r/min，实现了将共振转速移出常用转速范围。

(3)结构参数优化后，仿真分析比较了结构参数优化前后系统的动态变化。电机轴角加速度频域响应最大减小了25.9%；输出轴最大转速减小了0.26%，整体波动明显减小，从而推断出结构参数优化后，系统平顺性明显得到提高。