建筑用太阳能热管式光伏光热系统优化

王瑞祥, 常旭东, 唐文涛, 吴会娇

(1.北京建筑大学北京市建筑能源高效综合利用工程技术研究中心，北京 100044；2.北京同创绿源能源科技有限公司，北京 102209)

太阳能有效利用在建筑节能中起着重要的作用。热管式光伏光热系统是太阳能建筑的一种有效的能源利用方式。有学者提出对于太阳能光伏系统，光伏电池温度每升高1 ℃，光伏效率就会下降约0.5%[1]。热管式光伏热(photovoltaic & thermal,PV & T)系统能够有效利用未被太阳能电池吸收的辐射以及太阳能电池产生的热量，降低太阳能电池工作温度，对提高光伏光热效率具有重要意义。

通过建立数学模型，对其中的参数进行研究优化是一种提高效率的手段。郭嘉等[2]建立了太阳能PV & T系统的热电模型，研究了PV & T系统在呼和浩特市每个季节的光伏光热效率、电池温度的变化，并与实验对比，验证了此数学模型的精度。Khelifa等[3]对PV & T系统节点的能量平衡方程为基础建立数学模型，采用有限差分法求解，优化后获得了69%的综合效率并进行了实验验证。

Moradgholi等[4]将热管技术引入光伏发电系统以提高效率和增加热能利用的设想并使用热管式PV & T系统进行了实验对比，发现在夏季集热器倾角为40°以及使用丙酮作为热管内工质时热效率达到了45.14%，且发电效果明显好于普通的PV & T系统。Gang等[5]设计并构建了一种新型的热管式PV & T系统，建立了系统性能预测的动态模型，通过对比实验结果，认为该模型可以得到满意的预测结果。陈红兵等[6]搭建热管式PV & T系统，分别以水和相变流体作为工质，分析了在同样的工况下两个系统的光伏板表面温度、换热水箱温度、热/电功率、热/电效率及综合效率。

为了更好地将太阳能的利用纳入建筑用能系统及建筑物理环境的总体设计，需要对建筑用热管式光伏光热系统优化。为此，分析研究热管式PV & T系统，分析其动态物理过程，建立改进[7]后的热管式PV & T系统的数学模型，并对系统进行了优化分析。

1 热管式PV & T系统

1.1 系统组成及工作原理

热管式太阳能光伏光热系统主要由热管式PV & T集热板、水泵、水箱、太阳能控制逆变器、蓄电池等组成。图1为系统的原理示意图。其中，热管式PV & T集热板主要由玻璃盖板、光伏电池、黏合层、吸热基板、热管、保温及联箱组成。图2为集热器的截面示意图。

当系统开始运行之后，热管式PV & T集热器接收太阳辐射。一部分短波太阳能辐射被太阳能电池吸收，转化为电能，输送到蓄电池或直接供给负载。其他辐射被集热器吸收转化为热能，电池中的热能传递到吸热基板，被热管蒸发段吸收，并且通过热管内部液体的相变传热，将热量传递至冷凝段。热管冷凝段在联箱中将热量传递给水流，热水流至水箱中。

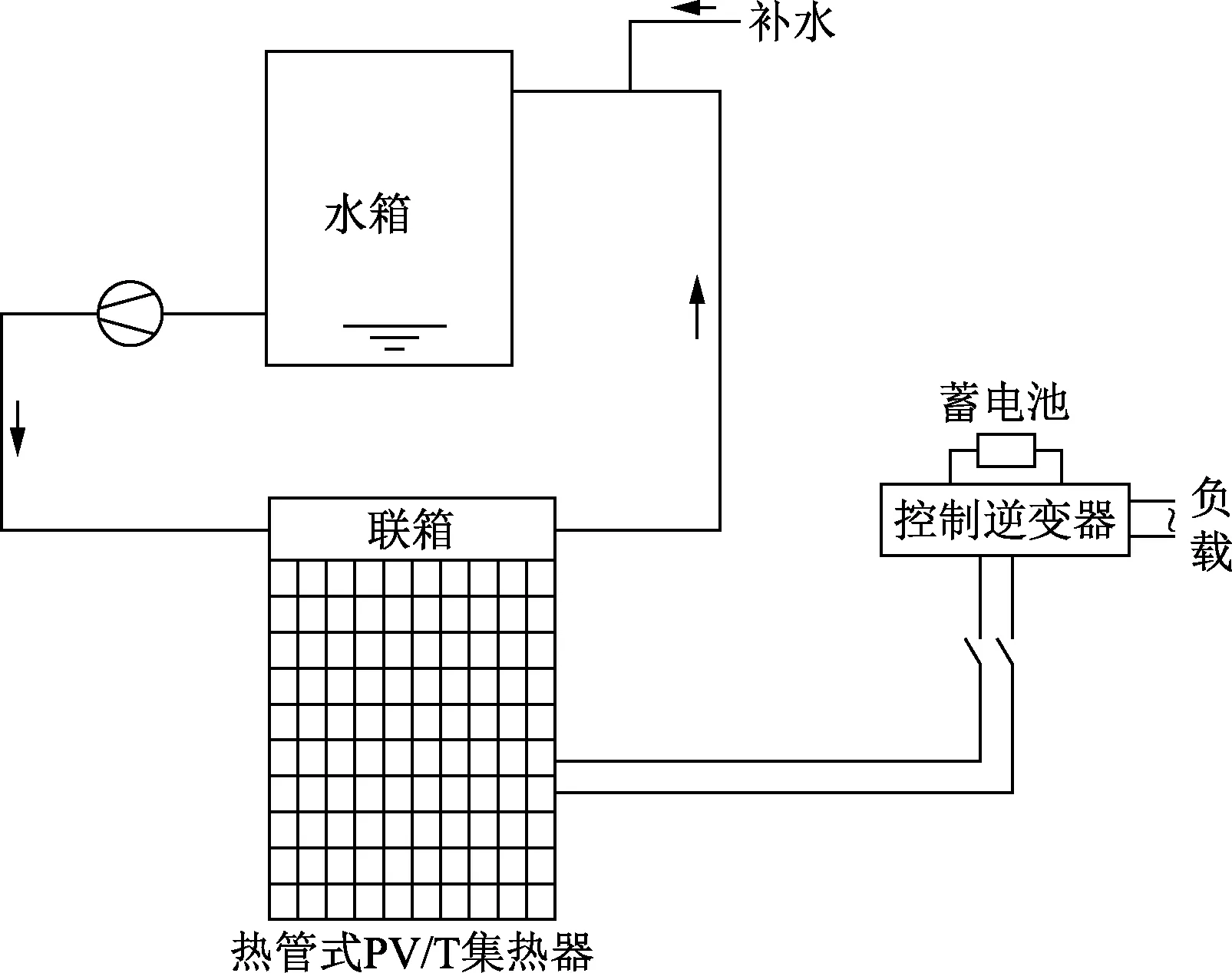
图1 系统原理示意图Fig.1 Schematic diagram of system

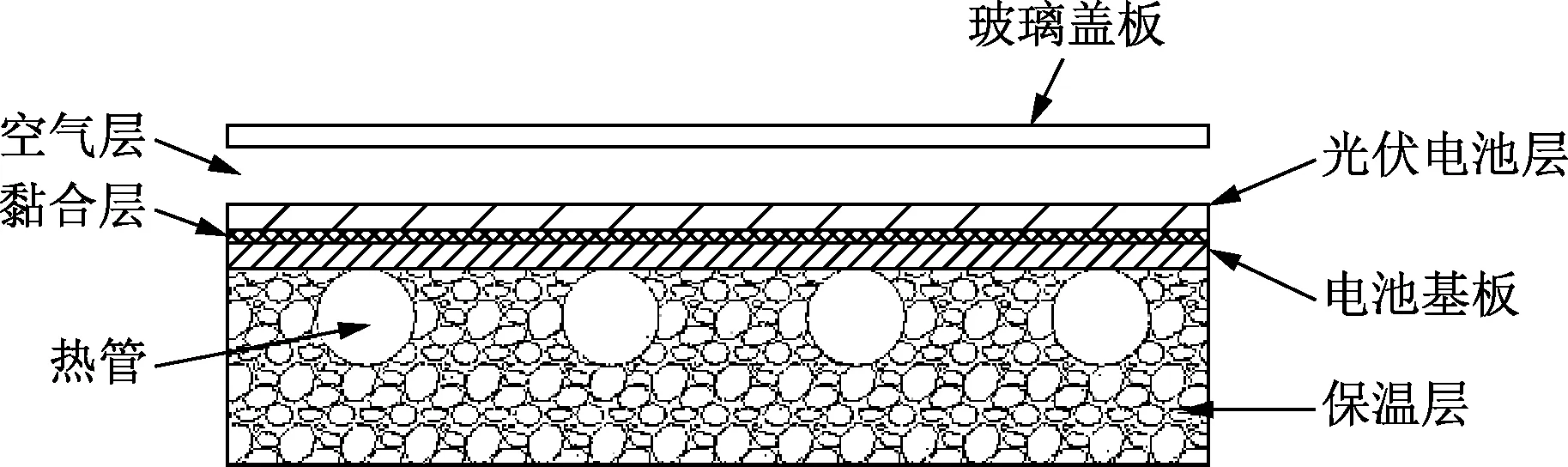
图2 集热器截面示意图Fig.2 Cross section diagram of collector

1.2 系统热物理过程分析

太阳光首先照射到热管式PV & T集热器的玻璃盖板，盖板会吸收一部分太阳能量，在这一部分的热量交换包括玻璃盖板与周围环境空气发生对流换热、与周围环境发生辐射换热以及与光伏电池间的换热。太阳辐射通过玻璃层照到电池上，光伏电池吸收一些太阳能，转化为电能。其余辐射变为热能，一部分热量与玻璃盖板产生换热，另一部分热量与电池基板产生导热。热量被基板吸收后，产生了三部分的热量交换，分别是电池基板与光伏电池间的导热、电池基板与周围环境的换热以及与热管蒸发段的导热。之后，由热管蒸发段吸收电池基板的热量，通过热管内部的毛细作用，将热量传递至冷凝段。热管冷凝段插入联箱中，与联箱中的水对流换热。联箱中的水吸收了热管的热量后，流向水箱中，以此不断循环。系统的能量流动流程如图3所示。

Tg为玻璃盖板的温度；Ta为周围环境空气温度；Tpv为光伏电池温度；Tb为电池基板的温度；Tp,eva为热管蒸发段的温度；Tp,con为冷凝段的温度；Tw为流道换热器内的冷却水温；Twt为储水箱内的水温；A为集热板面积；Aw为流道换热器内水和热管冷凝端的换热面积；G为太阳辐照强度；αg为玻璃盖板对太阳光的吸收率；hag为玻璃盖板与周围环境空气的对流换热系数；hg,pv为玻璃盖板与电池层的总换热系数；ταpv为光伏电池层对太阳光的有效吸收率；Epv为光电功率；hw为联箱中水和热管冷凝端的表面换热系数；Rb,pv为光伏电池层与电池基板间的热阻；Rb,a为基板同周围环境之间的热阻；Rp,b为电池基板与热管蒸发段管壁间的热阻；Re,c为热管蒸发段与冷凝段之间的热阻；Rw,a为冷却水与空气间的热阻；Ra,wt为水箱内水与外界间的总热阻图3 系统能量流动流程Fig.3 System energy flow

2 数学模型及验证

2.1 数学模型的建立

2.1.1 系统效率

效率是体现一个系统性能的主要指标，对于热管式光伏光热系统，其效率指标分别为光电光热综合效率ηpv,t、光热效率ηt、光电效率ηpv，其计算公式如式(1)～式(3)所示。

系统全天平均光电光热综合效率ηpv,t:

ηpv,t=ηt+ζηpv

(1)

式(1)中：ζ为光伏电池覆盖因子。

系统的全天平均光热效率：

(2)

式(2)中：Ht为系统集热板全天接收到的总太阳辐射；Qw为系统全天得热量。

系统的全天平均光电效率：

(3)

式(3)中：Epv为光电功率。

计算光电光热综合效率ηpv,t、光热效率ηt、光电效率ηpv，需要得到系统全天的得热量以及系统的光电功率，计算公式如式(4)、式(5)所示。

系统全天总得热量：

Qw=Mwcw(Twt,f-Twt,i)

(4)

式(4)中：Mw为储水箱内水的总质量，kg；cw为水的比热容，J/(kg·K)；Twt,i和Twt,f分别为系统的初始水温和终水温，K。

光伏电池的光电功率：

Epv=ζGτηr[1-Br(Tpv-Tr)]

(5)

式(5)中：G为太阳辐照强度，W/m2；ηr为光伏电池在参考温度Tr下的光电转换效率，一般取Tr=298.15 K；τ为电池封装材料的总透过率；Br为电池的温度系数，取值为0.004 5 K-1。

为了计算系统得热量和光电功率，需要求得系统的水温以及光伏电池层的温度，所以根据所分析的系统动态热物理过程，参考符慧德[7]所建立的方程，建立了热管式PV & T集热器每个部件的能量平衡方程，根据能量平衡方程，联立求解系统每个部件的温度，最终求得系统的光热效率及光电效率。

2.1.2 玻璃盖板层

忽略玻璃盖板的横向及纵向导热，认为其温度分布均匀，建立能量平衡方程:

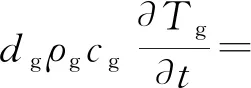
hg,pv(Tpv-Tg)+Gαg

(6)

式(6)中：dg为玻璃厚度，m；ρg为密度，kg/m3；cg为比热容，J/(kg·K)；Tg为玻璃盖板的温度，K；Ta为周围环境空气温度，K；Tpv为光伏电池温度，K；Tsky为天空温度，K；ha、hsky、hg,pv分别为玻璃盖板与周围环境空气的对流换热系数、与周围环境间的辐射换热系数、与电池层的总换热系数，W/(m2·K)；G为太阳辐照强度，W/m2；αg为玻璃盖板对太阳光的吸收率。

与文献[7]建立的方程不同，使用天空温度Tsky代替环境等效温度，环境等效温度为空中温度、地面温度、周围环境温度的综合等效温度。在计算当中，需要分别测量其中这几项温度，且要求得玻璃盖板分别与天空、地面、周围环境的视角系数。为了简化计算，由于天空温度占环境等效温度的比重最大，所以使用天空温度代替环境等效温度进行计算。

2.1.3 光伏电池层

由于TPT以及黏合层的厚度非常薄，并且热容很小，所以忽略这部分的导热，建立能量平衡方程：

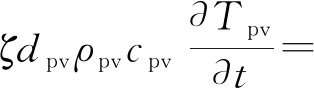
G(τα)pv-Epv

(7)

式(7)中：dpv为光伏电池的厚度，m，ρpv为密度,kg/m3；cpv为比热容，J/(kg·K)；Tb为电池基板的温度，K；Rb,pv为光伏电池层与电池基板间的热阻，(K·m2)/W；ταpv为光伏电池层对太阳光的有效吸收率；ζ为光伏电池覆盖因子。

2.1.4 吸热基板层

(Tp,eva-Tb)/Rp,b

(8)

式(8)中：ρb为电池基板的密度，kg/m3；cb为比热容，J/(kg·K)；db为电池基板的厚度，m；Rb,a为基板同周围环境之间的热阻，(K·m2)/W；Tp,eva为热管蒸发段的温度，K；Rp,b为电池基板与热管蒸发段管壁间的热阻，K/W。

2.1.5 热管的能量平衡方程

热管热传导能量平衡方程，分为热管蒸发段和热管冷凝段两部分计算。

热管蒸发段能量平衡方程：

(Tb-Tp,eva)/Rp,b

(9)

式(9)中：Mp,eva为蒸发段的总质量，kg；cp为热管管壁的比热容，J/(kg·K)；Tp,con为冷凝段的温度，K；Re,c为热管蒸发段与冷凝段之间的热阻，按式(10)计算：

Re,c=Re,p+Re,i+Rc,i+Rc,p

(10)

式(10)中：Re,p为蒸发段管壁的径向导热热阻，K/W；Re,i为蒸发段毛细管芯的径向等效传热热阻，K/W；Rc,i为冷凝段蒸汽凝结传热热阻，K/W；Rc,p为冷凝段管壁的径向导热热阻，K/W。

热管冷凝段能量平衡方程：

Awhw(Tw-Tp,con)

(11)

式(11)中：Mp,con为热管冷凝段的总质量，kg；Tw为流道换热器内的冷却水温，℃;Aw为流道换热器内水和热管冷凝端的换热面积，m2；hw为联箱中水和热管冷凝端的表面换热系数，W/(m2·K)。

2.1.6 联箱

建立联箱内的能量平衡方程如式(12)所示：

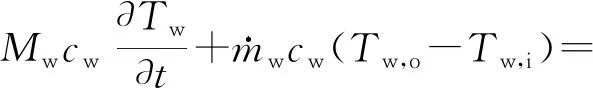
Awhw(Tp,con-Tw)

(12)

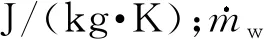
2.1.7 储水箱

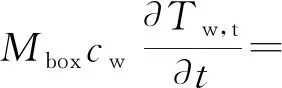
(Tw,o-Tw,i)

(13)

式(13)中：Mbox为储水箱内水的总质量，kg；Ra,wt为水箱内水与外界间的总热阻，K/W；Twt为储水箱内的水温，K；n为集热器的数目。

2.2 初始条件

2.2.1 气象参数

选取北京市春分日、夏至日、秋分日、冬至日的气象条件进行计算，气象参数参考自中国气象数据网(http://data.cma.cn)。

2.2.2 设计参数

根据图2所示的热管式PV & T集热器的结构图，主要设计参数整理如表1所示。

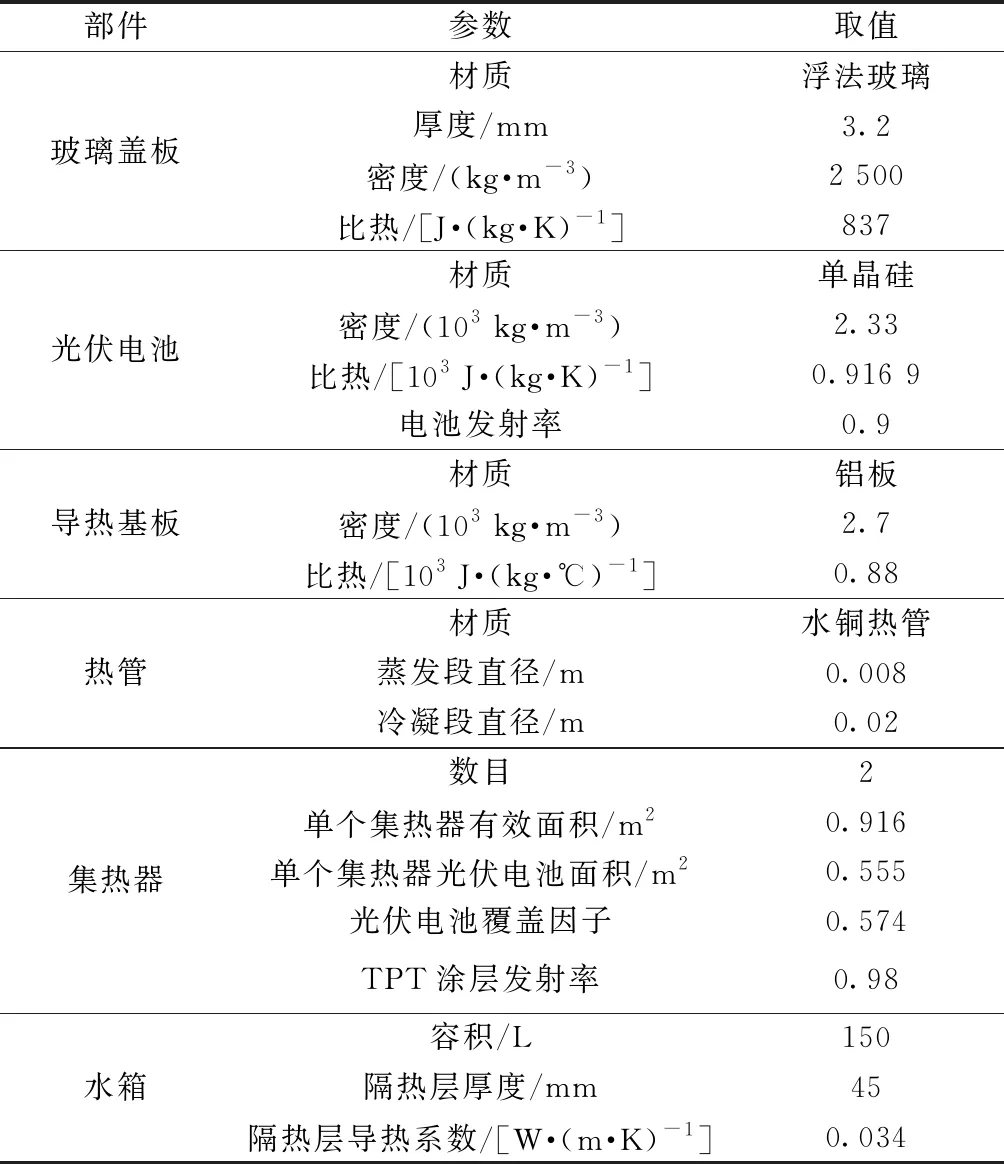
表1 主要设计参数Table 1 Main design parameters

2.3 模型验证

为验证所建立数学模型的可靠性，首先将设计参数，以及气象条件等参数代入数值模型当中，使用MATLAB软件进行编程计算。应用建立的数学模型，以30 min为步长，进行9：00—16：00的数值计算。此次模型验证计算中，模型参数采用与文献[5]相同的计算参数。将计算所得的数据与参考文献的实验数据进行比较，其结果如图4所示。研究表明造成光伏效率仿真误差，是由于集热器玻璃盖板的反射率是跟随太阳入射角不断变化的。由对比结果可知，所建立的数学模型可靠。

图4 仿真计算结果与文献实验数据对比Fig.4 Comparison of simulation results with experimental data in literature

3 计算及优化结果

3.1 模型计算

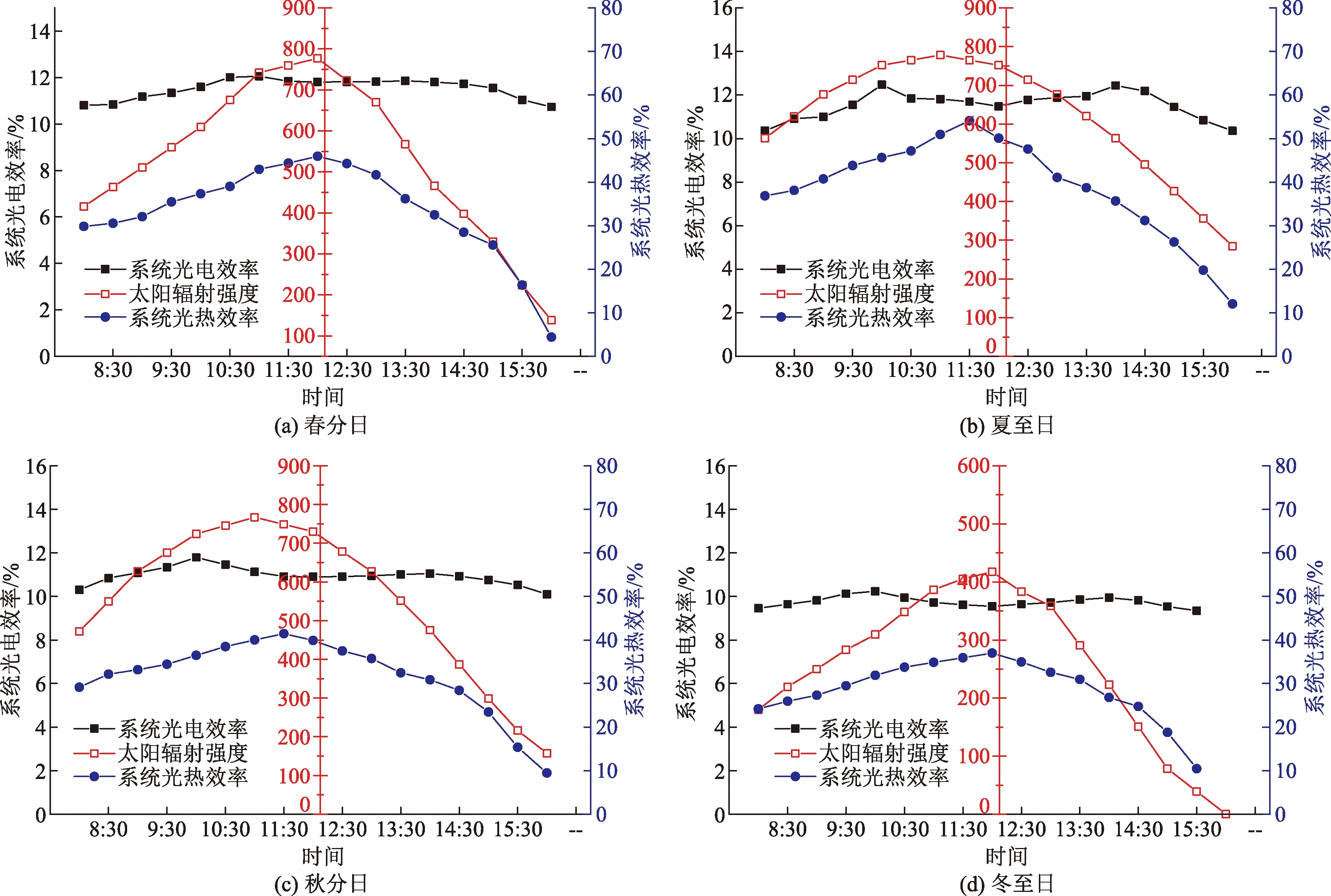
图5 太阳辐射强度、系统光电效率和系统光热效率曲线Fig.5 Curves of solar radiation intensity, photoelectric efficiency and photothermal efficiency of the system

首先将设计参数及气象条件等参数代入到数值模型当中，使用MATLAB软件进行编程计算。应用建立的数学模型，以30 min为步长，进行8：00—16：00的数值计算。计算结果如图5所示。图5为北京市不同季节(春分日、夏至日、秋分日、冬至日)的太阳辐射强度以及系统光电效率和光热效率的理论计算值。系统的光电效率在计算时间段内，均主要维持在10%～12%，符慧德[7]认为太阳光对集热器表面的入射角较大，因此系统的光电效率值比较低。以及在计算过程中，采用的是集热器表面所接受的总太阳辐射，未考虑散射辐射、直射辐射等因素的影响，所以会造成在进行系统光电效率时，会产生一些偏差。春分日全天最大的光电效率为12.05%，夏至日全天最大的光电效率为12.47%，秋分日全天最大的光电效率为11.79%，冬至日则为10.23%。夏至日的光电效率为四个季节内最大的，主要是因为在夏季，室外温度较高，以及全天的太阳辐射强度较其他季节相比要高出很多。冬季的光电效率最低，因为室外温度以及太阳辐照量较低，使得光伏系统的发电量较低。但是在全天当中，由于在正午时刻太阳辐射强度最大，导致了正午时，系统的光电效率最低。

光热效率可以看出与全天太阳辐射强度变化趋势相同。其光热效率同样随着光热功率的变化而变化，系统的光热效率在中午达到最大值，下午逐渐降低，由于系统的光热功率在逐渐下降。在正午12:00左右，太阳辐射强度最强，系统的光热功率达到最高值。下午系统的光热效率逐渐下降，光热功率逐渐接近为0，是因为下午太阳辐射逐渐降低，系统的水温逐渐上升，导致了系统热量损失增大。由四个季节比较，在夏季时，系统的全天光热效率最大，冬季的系统全天光热效率最低。

3.2 不同参数对系统性能影响结果分析

3.2.1 热管数量对系统性能的影响

热管的数量会影响热管式PV & T系统电池板热量的传递以及冷却效果，为研究不同热管数量对系统效率的影响，找到最佳热管数量，对热管式PV & T数值模型进行了不同热管数量的数值模拟计算。选择了北京市7月1日的气象数据(来源：中国气象数据网http://data.cma.cn)作为条件进行计算仿真。计算结果如图6、图7所示。

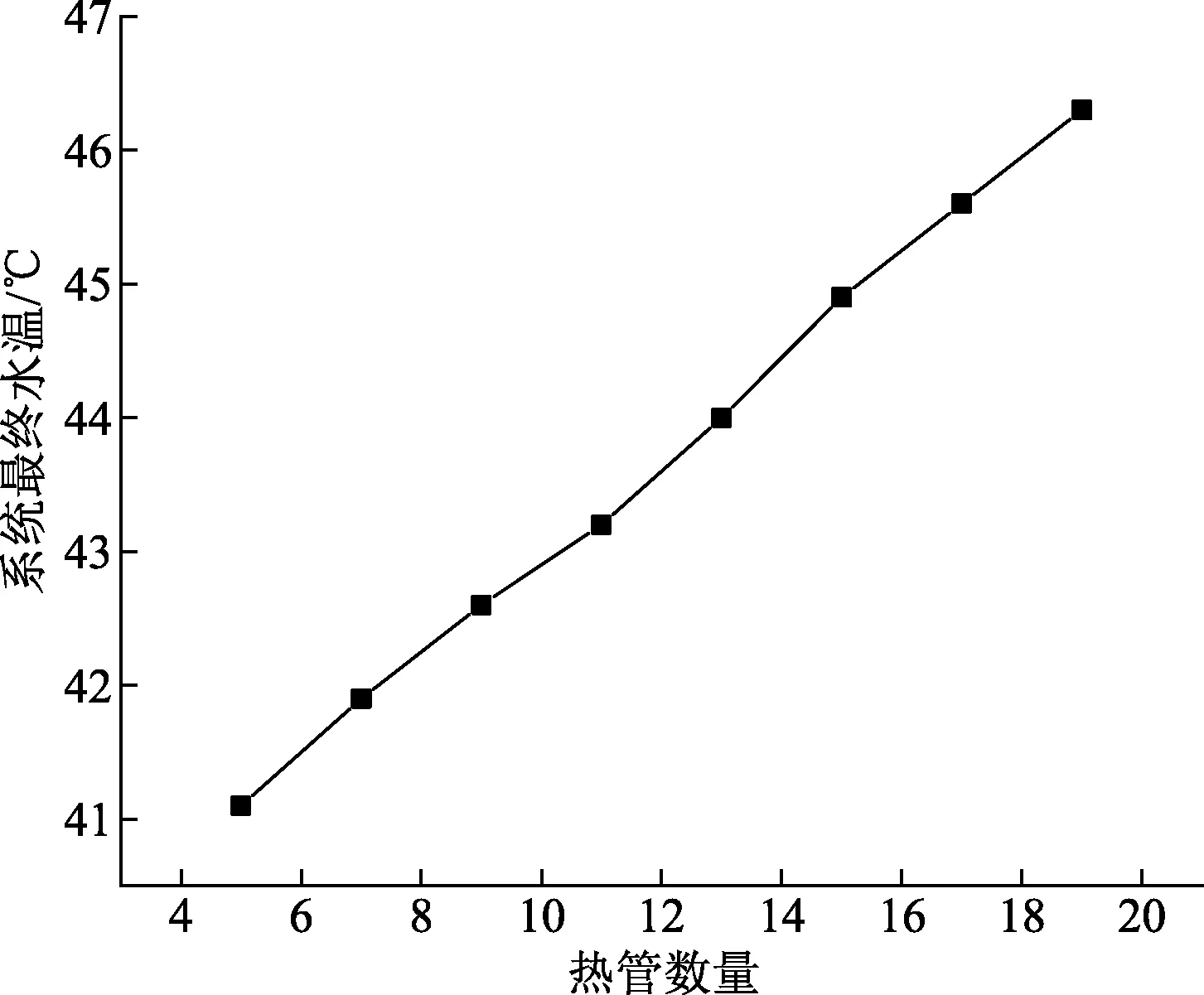
图6 系统最终水温随热管数量变化曲线Fig.6 The final water temperature of the system as a function of the number of thermal pipe

图7 光电效率、光热效率随热管数目变化曲线Fig.7 Photoelectric efficiency and photothermal efficiency as a function of the number of heat pipes

由图6可知，热管数量越大，系统的最终水温越高。当热管数量为5时，系统的平均水温由27.8 ℃升高到41.1 ℃，计算时刻总体升温13.3 ℃；当热管数量为19:00，系统的平均水温由27.8 ℃升高到46.3 ℃，计算时刻总体升温18.5 ℃，与热管数量为5根时相比，增加了5.2 ℃。

由图7可知，系统的光电效率及光热效率都会随着热管数量的增加而增大，这是因为热管数量增加，增大了热管与光伏电池板的换热面积，使得换热效果增加，冷却了光伏电池板，使得光电效率和光热效率得以提升。在热管数量小于11时，系统效率的上升速率比较快，但是随着热管数量的逐渐增加，系统效率的增加速率逐渐减缓。考虑到系统的收益、性能以及成本，认为热管式太阳能PV & T系统选择的热管数量为9～11根为宜。

显然，热管的数量会影响系统的光电效率及光热效率。但是热管本身物理性质，以及热管的结构，都会影响到热管本身的传热效果，必定也会对整个系统的效率产生影响。张涛[8]则是对热管构造进行了改良，搭建了环形热管式PV & T系统，将集热器作为热管蒸发段，热管的冷凝段则是水箱中的盘管，将系统的性能得到了良好的改善。

3.2.2 集热器倾角对系统性能的影响

热管式PV & T集热器与地面之间的夹角同样是影响系统性能的因素之一。因为地球在不停地自转与公转，所以太阳光的照射角度在不停变化，若想尽可能地吸收太阳辐射，最好的解决办法是设置太阳能追踪式集热器，但是这种集热器成本较高，所以，就要找到集热器的最佳设置倾角，确保系统能够产生最大的收益。已有相关文献对单独的太阳能电池板或集热板的倾角做了研究，何世钧等[9]考虑了系统安装的位置、时间、环境温度和热负荷等条件对系统集热量影响，确定了集热器最佳倾角的方法。朱丹丹等[10]通过倾斜面太阳辐射计算模型和光伏电池电力输出模型的建立，分析了倾斜面全年太阳辐射总量随倾斜角的变化规律。本部分将对不同集热板倾角对系统效率的影响进行分析。分别计算了系统在春分日、夏至日、秋分日和冬至日在不同集热器倾角的情况下，系统的光电效率和光热效率。计算角度为10°～80°，每隔5°计算一次系统效率。

由图8可知，系统的全天平均光电效率与光热效率均呈现先增大后减小的趋势。这是由于在集热器达到最佳倾角时，系统所吸收的太阳能辐射最大，当倾角改变后，集热器所接收的太阳能辐射减少，所以系统产的光电功率与光热功率减少，导致了效率下降。由图8可知，当集热器的倾角分别为45°、35°、40°、50°时，在春分、夏至、秋分、冬至四天内，系统效率达到最大。由于天气原因，热管式PV & T系统在冬季所产生的光电功率和得热量比较低，在夏季比较高。且这四个日子的计算时刻内所接受到的太阳辐射分别为9 026.15、10 523.21、9 710.63、4 482.18 W/m2。在夏季到秋季两个季节内，室外温度及太阳辐射比较强烈，所以综合考虑，建议将集热器倾角设置在35°～40°。

图8 系统光电效率、光热效率随集热器倾角变化曲线Fig.8 The curve of photoelectric efficiency and photothermal efficiency of the system changing with the angle of collector

为了计算出确切的集热器倾角数值，将参照太阳辐射强度作为依照，计算不同倾斜角度下，斜面所接收到的太阳辐射量。计算集热器斜面上的太阳辐射数学模型公式如式(14)所示[11]：

Hd(2+cosβ)/3+Hρ(1-cosβ)/2

(14)

式(14)中：Hz为到达斜面上的太阳辐射；Hh为水平面上直接辐射；Hd为水平面上散射辐射；ωc为倾斜角为β的日出日没时角；ωo为水平面上的日出和日没时角；φ为当地纬度；β为集热器安装倾角；δ为太阳赤纬；ρ为地面反射率；H为水平面太阳辐射总量。

图9为按照数学模型式(14)计算得出的北京市斜面年太阳辐射量随倾角变化的曲线。由图9可知，辐射总量随集热器倾角先增大后减小，在38°时达到最大值。其计算值在通过分析光伏光热效率所分析得到的35°～40°。综合考虑，建议将集热器倾角设置为当地纬度值或略小于当地纬度1°～2°。

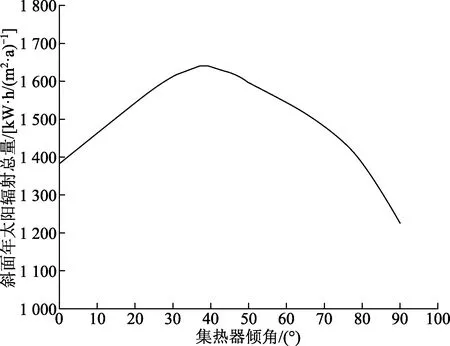
图9 北京市集热器倾斜面年太阳辐射总量随倾角变化曲线Fig.9 The variation curve of total annual solar radiation on inclined surface with inclination angle of collector in Beijing

4 结论

建立热管式光伏光热系统的数学模型，通过模型来计算出系统热效率和电效率。并且对影响系统的主要参数进行了计算，以北京地区7月某天的天气状况为计算依据，发现随着热管数量的增加，系统的效率也会逐渐增大，但考虑到成本及其他问题，认为集热器热管数量选择9～11根为宜。以春分日、夏至日、秋分日和冬至日的气象参数为条件，进行了集热板倾角对系统性能影响的探讨，由于每个季节太阳高度角不同，温度和太阳辐射强度不同，所以每个季节的最佳集热器倾角也不同。通过计算，综合考虑到斜面所接收到太阳辐射总量，认为北京地区全年将集热器倾角设置为38°较为适宜。