非金属元素掺杂二硒化钨/石墨烯异质结对其肖特基调控的理论研究*

马浩浩张显斌魏旭艳 曹佳萌

(西安理工大学理学院， 西安 710048)(2020 年1 月12日收到; 2020 年3 月23日收到修改稿)

采用平面波超软赝势方法研究了非金属元素掺杂对二硒化钨/石墨烯肖特基电子特性的影响. 研究表明二硒化钨与石墨烯层间以范德瓦耳斯力结合形成稳定的结构. 能带结果表明二硒化钨与石墨烯在稳定层间距下形成n型肖特基势垒. 三维电子密度差分图表明石墨烯中的电子向二硒化钨移动， 使二硒化钨表面带负电， 石墨烯表面带正电， 界面形成内建电场. 分析表明， 将非金属原子掺杂二硒化钨可以有效地调控二硒化钨/石墨烯肖特基势垒的类型和高度. C， O原子掺杂二硒化钨时， 肖特基类型由p型转化为n型， 并有效降低了肖特基势垒的高度; N， B原子掺杂二硒化钨时， 掺杂二硒化钨体系表现出金属性， 与石墨烯接触表现为欧姆接触. 本文结果可为二维场效应晶体管的设计与制作提供相关指导.

1 引 言

随着半导体工艺的不断进步， 工艺尺寸越来越接近硅工艺的极限， 单位面积内集成的晶体管数量不断提高导致功耗不断增加， 摩尔定律受到了严峻的挑战[1-4]. 近年来， 二维材料由于其优异的电学、光学、力学、热学性质， 有望代替硅成为下一代主流的半导体材料[5-9]. 例如最早发现的二维材料石墨烯(graphene)， 具有优异的导热性能[10](3 ×103W/(m·K))和力学性能[11](1.06 × 103GPa)、室温下具有较高的电子迁移率[12](1.5 × 104cm2·V—1·s—1)等， 在新能源储存[8]、电磁干扰屏蔽[13]、集成电路[14]、场效应晶体管[15]等领域具有广阔的应用前景， 但零带隙使得graphene晶体管很难具有器件的开关状态， 尽管利用特殊基底、掺杂、光刻[16]等方法使得graphene获得能带间隙， 但其间隙范围仍然较小(＜ 1.0 eV)， 且这些方法会导致graphene导电性能降低， 这很大程度地限制了其在电子器件领域的应用.

2010年， 过渡金属硫化物(TMDs)材料的出现突破了graphene在电子器件中的局限性[17]. 与graphene不同的是， TMDs材料具有令人满意的禁带宽度(例如: 能带间隙为1.2—1.9 eV的二硫化钼、能带间隙大于2 eV的单层WS2材料等)以及较高的电子迁移率(例如室温下二硫化钼迁移率为200 cm2·V—1·s—1)[18，19]. 通过改变TMDs材料层数、外加偏压、材料应变等方式可对其能带结构进行1—2 eV可靠调控， 当TMDs材料由体相降低到单层时， 会由间接带隙转变为直接带隙， 其电学、光学性能也会发生显著变化. 这些优势使TMDs被广泛应用在高性能纳米电子器件和光电器件中. TMDs材料化学式是MX2， M是指过渡金属元素(例如: 钼、钨、铌、铼、钛)， X是指硫族元素(例如: 硫、硒、碲). 块状TMDs像石墨一样， 可被剥离成单层或者多层的纳米片. 与graphene相比较， 单层TMDs呈现一种X-M-X的三明治结构， 具有半导体或超导性质， 并且带隙具有可控、可调的性质[20，21]. 近年来， WSe2作为TMDs材料中的一员， 也备受关注[22-24]. 当二维WSe2从多层转变成单层时， 其能带结构发生了变化[25，26]. 一方面， WSe2由间接带隙转变成直接带隙， 并且发生了谷间自旋耦合; 另一方面， 多层WSe2带隙为1.2 eV，而单层的WSe2带隙为1.65 eV[21]. 2012年， Fang等[27]基于单层WSe2化学吸附NO2表面掺杂，制备出高性能p型场效应管， 在室温下有效空穴迁移率高达250 cm2·V—1·s—1， 并且ION/IOFF＞106.2015年， Zhou等[28]应用化学气相沉积方法制备出大面积单层WSe2材料， 并利用单层WSe2材料制作了p型场效应晶体管， 发现单层WSe2具有良好的晶体质量， 在室温下单层WSe2有效的空穴载流子迁移率高达100 cm2·V—1·s—1. 2019年， 王丹等[29]通过氢化单层WSe2表面， 发现氢化可产生p型掺杂的效果， 即氢化WSe2材料可制作p型场效应晶体管. 由于单层WSe2具有优异的光电性能， 其带隙能够满足电子器件和光电器件的大部分需求， 并且单层的WSe2也是首个被发现其输运性质可以调整为有p型或者双极性行为的半导体材料. 这些性质使得WSe2在场效应晶体管中具有极大的应用价值.

近年来， 将两个或多个二维材料组合应用于肖特基二极管、场效应管、光电器件以及集成电路等已成为研究的热点[2，30-33]. 二维TMDs材料可以和各种二维材料结合制备异质结， 并且晶格失配率较低[34]. 因此， TMDs材料与其他二维金属材料结合构成异质结是新一代场效应晶体管的基石[35，36].2013年， Liu等[37]用Ti和Au与单层WSe2接触形成金属-WSe2肖特基， 发现在高负电荷下有一个很小的空穴电流， 比电子电流低3—5个数量级.其机理在于界面处的肖特基势垒高度削弱了空穴传输. 由金属和二维TMDs材料界面形成的肖特基势垒， 往往会降低空穴的注入效率， 从而降低场效应晶体管的性能， 这极大的限制了二维TMDs材料在场效应晶体管中的应用[38]. 2014年Tosun等[39]用金属Pt， K与单层WSe2接触用于降低肖特基势垒高度(SBH)， 发现K与WSe2接触时单层的WSe2表现为n型， Pt与WSe2接触时单层的WSe2表现为p型， 且ION/IOFF＞104电流增益大于12. 2015年， Lee等[40]用金属Co与单层WSe2接触形成肖特基时， 电子迁移率增强， 但是WSe2由p型转化为n型. 其机理是Co金属和WSe2界面接触费米能级上移， 费米能级达到平衡后导电通道电子输运能力取决于导带最小值(CBM). 2019年， 谭淼等[41]研究了WS2/WSe2，WS2/WTe2和WSe2/WTe2等范德瓦耳斯异质结的结构和性质， 发现这3种范德瓦耳斯异质结都为n型. 值得注意的是， 虽然基于二维TMDs材料的场效应晶体管研究众多， 但其多为n型场效应晶体管， 而p型场效应晶体管的制备仍然是一个巨大的挑战. 虽然引入金属原子可以降低SBH， 但多为n型场效应晶体管， 只有引入Pt原子才为p型场效应晶体管. 总之， 这些研究表明， 设计低SBH的TMDs/金属触点相对比较困难， 这限制了基于TMDC材料场效应晶体管的发展.

随着实验研究和理论研究的不断深入， 人们对设计较低的SBH和调控肖特基类型问题进行了大量的研究. 2014年， Chuang等[42]利用化学或静电高度掺杂graphene， 制备出具有n型和p型的WSe2场效应晶体管， 电子迁移率高达330 cm2·V—1·s—1，空穴迁移率高达270 cm2·V—1·s—1. 2017年， Tang等[43]通过CVD技术对graphene源极/漏极进行掺杂，生长出graphene/WSe2横向异质结的场效应晶体管， ION/IOFF可提高2个数量级至108， 并获得单极p型特征， 但其制作工艺复杂且不能大规模生产. Yue等[44]报道了一种大规模、高质量的MoS2(1—x)Se2x/graphene异质生产方法， 该异质结具有可控结构和光电晶体管的电子性能. 2020年，Qiu等[34]在异质结WSe2/graphene中引入W及Se空位， 发现空位的引入对WSe2的电子结构有很大的影响， 特别是W空位的影响要大于Se空位的影响. 这些研究表明， 化学掺杂可以有效的控制WSe2/graphene肖特基的类型， 降低肖特基势垒高度， 提升WSe2/graphene异质结的电学性能(如电子或空穴的迁移率， 开关比等). 值得注意的是， 大量的研究者在WSe2/graphene肖特基中引入的原子多为金属原子， 使得单层WSe2很容易从p型转化为n型. 与金属相比， graphene在常温下具有较高的电子迁移率， 电阻率为10—6Ω·m比铜和银更低[45]， 导热系数是铜、铝等金属的数10倍(导热系数: 5300 W/(m·K))， graphene的硬度超过金刚石，断裂强度达到钢铁的100倍[46].

本文采用平面波超软赝势方法研究了非金属原子(B， C， N， O)掺杂二硒化钨/石墨烯， 对界面相互作用和电子性质的影响. 掺杂异质结的能带结构讨论了掺杂对肖特基的影响， 确定了肖特基势垒的类型和高度.

2 计算方法

本文所有计算基于密度泛函理论(DFT)的平面波超软赝势方法(USP)[47]， 使用CASTEP模块完成[48]. 研究了WSe2(1—x)(B， C， N， O)2x/graphene异质结界面相互作用和电子性质， 检测了界面电荷的重分布， 确定肖特基势垒的类型和高度. 在建立异质结前， 首先采用广义梯度近似[49](GGA) 的Perdew-Burke-Ernzerhof (PBE)方法对单层六方相WSe2(空间群为P63/mmc)晶胞进行几何优化， 其晶格常数为a = b = 0.330 nm. 同时对graphene晶胞进行几何优化， 其晶格常数为a =b = 0.246 nm. 优化后的计算结果与已报道的实验值误差小于1% (WSe2: a = b = 0.327 nm; graphene:a = b = 0.246 nm)[1，50]. 本文所涉及的超晶胞结构以几何优化后的晶胞为基础来展开后续计算分析.

根据优化后的晶格常数选取单层WSe2的周期结构为3 × 3 × 1， 随机选取一个Se原子分别被B， C， N， O取代， 如图1所示. 以此结构为基础与周期结构为4 × 4 × 1的graphene进行异质结匹配， 由此构成WSe2(1—x)(B， C， N， O)2x/graphene异质结. 为了精确描述层间范德瓦耳斯力[51]， 在GGA-PBE方案中选择了Tkatchenko-Scheffler(TS)[52]色散修正， 此色散修正得到体系的总能量可表示为Etotal= EKS-DFT+ Evdw， 其中， EKS-DFT表示传统Kohn-Sham DFT计算得到体系的总能量， Evdw表示由层间范德瓦耳斯力产生的能量. 在描述原子核与电子之间的相互作用时， 选取的电子组态分别为C: 2s22p2; W: 5d46s2; Se: 4s24p4. 布里渊区网格选取为5 × 5 × 1[53]， 每个原子位移不超过5 × 10—4nm， 每个原子所承受的应力不超过0.07 GPa， 平面波动能截断为450 eV， 自洽收敛精度为2.0 × 10—5eV/atom， 原子间受力不超过0.05 eV/nm. 真空层厚度设置为1.5 nm.

3 结果与讨论

3.1 结构稳定性

基于图1建立的4种物理模型， 为了深入研究异质结的匹配情况， 计算了WSe2(1—x)(B， C， N，O)2x/graphene异质结的晶格失配率. 设定优化后异质结晶格常数为a'， 单层二硒化钨超胞晶格常数为a1， graphene超胞晶格常数为a2， 定义晶格失配率为σ = (a2— a1)/a1. 如表1所示， 5种不同异质结其晶格适配率都不超过1%， 满足完全共格(|σ|＜ 5%)条件. 结果表明4种不同掺杂异质结的晶格适配率都小于WSe2/graphene异质结， 这是由于掺杂原子半径都小于Se原子半径. 随着掺杂原子半径逐渐增大(即RO＜ RN＜ RC＜ RB)[54]， 晶格失配率呈现出先下降后上升的趋势， 当硼原子掺杂WSe2/graphene异质结时晶格失配率最大. 这是由于Se原子p轨道有4个电子， 随着掺杂元素p轨道电子逐渐减少， 其得电子能力逐渐减弱，而当p轨道仅有1个电子时， 其表现出较强的失电子能力. 值得注意的是， 二维材料可以承受很强的拉伸和挤压. 根据Xie等[55]的报道， 褶皱的graphene可以被拉伸至30%左右. 也有研究表明，氮化碳在晶格失配较大的情况下会发生波状变形，从而有效地降低晶格失配对表面应力的影响.

图 1 单层二硒化钨掺杂俯视图 (a) 单层二硒化钨3 × 3 × 1超胞掺硼俯视图; (b) 单层二硒化钨3 × 3 × 1超胞掺碳俯视图;(c) 单层二硒化钨3 × 3 × 1超胞掺氮俯视图; (d) 单层二硒化钨3 × 3 × 1超胞掺氧俯视图Fig. 1. Top views of monolayer WSe2 doping: (a) Top view of single layer WSe2 3 × 3 × 1 supercell boron doped; (b) top view of single layer WSe2 3 × 3 × 1 supercell carbon doped; (c) top view of single layer WSe2 3 × 3 × 1 supercell nitrogen doped; (d) top view of single layer WSe2 3 × 3 × 1 supercell oxygen doped.

表 1 不同非金属元素掺杂WSe2/graphene异质结的晶格失配率、形成能、结合能、晶格失配能参数Table 1. Lattice mismatch rate， formation energy， cohesive energy， and lattice mismatch energy parameters of WSe2/graphene heterojunction doped with different nonmetallic elements.

形成能是描述结构稳定性的重要参数， 在3 ×3 × 1周期结构的单层WSe2中掺B， C， N， O等原子时， WSe2(1—x)(B， C， N， O)2x的形成能[56]可表示为:

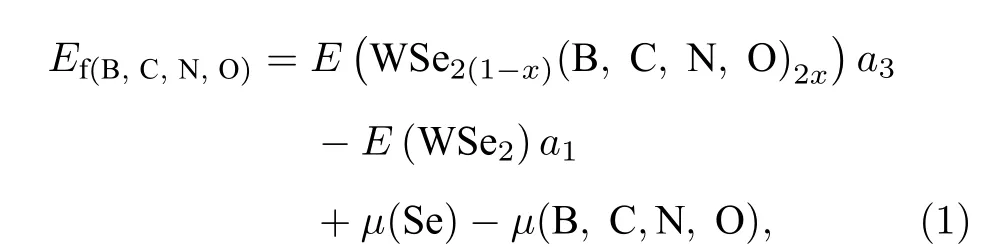
界面相互作用对异质结的电子有很大影响， 因此在讨论B， C， N， O掺杂对异质结电子的影响之前， 首先研究了B， C， N， O掺杂与界面相互作用的关系. 层间相互作用影响异质结界面结构的稳定性. 因此， 研究了WSe2(1—x)(B， C， N， O)2x/graphene热力学稳定性， 这里用结合能[57，58]来描述. 并将其定义为

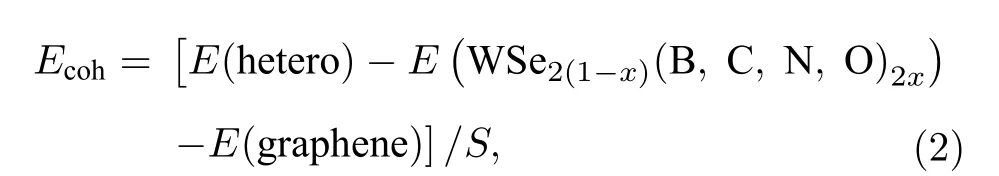
其中， E(hetero)为弛豫WSe2(1—x)(B， C， N， O)2x/graphene异质结; E(WSe2(1—x)(B， C， N， O)2x)为单层WSe2总能量; E(graphene)为graphene体系的总能量; S为WSe2(1—x)(B， C， N， O)2x/graphene异质结1/2表面积；Ecoh代表层间相互作用的能量，较低的Ecoh表示更稳定的界面结合. 如表1所示，WSe2(1—x)(B， C， N， O)2x/graphene异质结的界面结合能为—3.000 eV/nm2至—1.791 eV/nm2， 这表明稳定的界面结合. 在不掺杂原子的情况下异质结的界面结合能最大， 表明掺杂非金属原子可以提高该异质结的结构稳定性， 即掺杂减少WSe2/graphene异质结的总能， 使得界面结合更紧密.

利用晶格失配能可以进一步探究异质结的结构稳定性， 晶格失配能越小代表结构更加稳定.WSe2(1—x)(B， C， N， O)2x/graphene的晶格失配能[59]可表示为:

其中E (WSe2(1—x)(B，C，N，O)2x)a' 和E (graphene)a'分别表示晶格常数为 a' 时WSe2(1—x)(B，C，N，O)2x和graphene的总能量， E (WSe2(1—x)(B，C，N，O)2x)a1和E (graphene) a2表示晶格常数为a1和a2时WSe2(1—x)(B，C，N，O)2x和graphene的总能量. 由(3)式得出， ΔEmismatch为正值表示异质结不稳定.WSe2(1—x)(B，C，N，O)2x/graphene异质结的晶格失配能如表1所示， 晶格失配能为—7.022 eV/nm2至—1.690 eV/nm2. 在WSe2/graphene异质结中掺杂B， C， N， O时， 晶格失配能都低于WSe2/graphene异质结. 进一步表明掺杂非金属原子可以提高WSe2/graphene异质结稳定性， 此结论与界面结合能得出结论一致.

根据界面结合能、晶格适配能分析了WSe2(1—x)(B， C， N， O)2x和graphene的界面相互作用. 一方面， 两种物质相互吸引形成稳定的异质结， 使异质结构的总能量降至最低. 另一方面， 在WSe2(1—x)(B， C， N， O)2x和graphene形成稳定界面的过程中， 由于晶格的不匹配会产生失配能. 从异质结形成的整个过程来看， 两种物质在结合前需要克服晶格不匹配. 因此推测在WSe2(1—x)(B， C，N， O)2x和graphene之间范德瓦耳斯力相互作用应该包括晶格失配能和结合能， 即Evdw= |Ecoh| +|ΔEmismatch|. 从表1不难得出范德瓦耳斯力能由3.481 eV/nm2至9.896 eV/nm2， 接近之前报道的值[60]. 另外， 如果两种材料晶格失配率较大， 就不能形成稳定的范德瓦耳斯异质结. 本文中的计算结果没有超出这个范围.

3.2 能带结构

为了探究异质结层间相互作用对电子的影响，计算了异质结的能带. 在计算WSe2/graphene异质结能带时， 选用GGA-PBE近似方法， 布里渊区路径设置为G(0 0 0)-M(0 0.5 0)-K(—1/3 2/3 0)-G(0 0 0). 为了对比分析， 图2(a)和(b)分别为单层WSe2和graphene的能带图. 从图中可以看出单层WSe2为直接带隙， 在高对称G点处有1.62 eV的带隙， 计算结果略低于1.65 eV左右的实验数据[43]. 这是由于GGA-PBE近似方法在计算能带时低估了带隙值， 但这并不影响能带结构.因此， 在随后的计算中使用了GGA-PBE近似方法. 图2(b)显示graphene的价带和导带在M点(狄拉克点)交叉. 当外界环境改变， 如温度升高或光激励时， 价带的电子受激跃迁到导带， 结果表明graphene具有金属性质， 这与先前理论研究一致[61].

WSe2/graphene异质结能带图如图2(c)所示.与单层WSe2和graphene的能带对比， 异质结中graphene的狄拉克点仍然保留， 但是WSe2由直接带隙变为间接带隙(导带底在高对称点F， 价带顶在高对称点G)， 这是由于WSe2/graphene异质结构(0.333 nm)的层间平衡距离较小. 异质结构中单层WSe2的带隙由1.62 eV变为1.55 eV， 这说明夹层中存在范德瓦耳斯力. 从图2(a)—2(c)中可以看出， 异质结中graphene费米能级没有相对移动， 而WSe2费米能级相比于单层WSe2费米能发生了上移. 这是由于单层WSe2与graphene费米能级存在电势差. 当WSe2与graphene接触形成肖特基时， 界面电荷将会发生转移， 处于较高位置graphene的电子将流向WSe2. 因此， WSe2表面聚集了负电荷， graphene表面聚集了正电荷.

图 2 单层二硒化钨(a)、石墨烯(b)及二硒化钨/石墨(c)能带图， n型(p型)SBH介于二硒化钨的费米能级和最小导带(价带最大值)之间， 费米能级归一化设置为零， 用红虚线表示Fig. 2. Energy band structures of (a) monolayer WSe2， (b) grapheme， and (c) WSe2/graphene heterostructure. The n-type (p-type)SBH are indicated between the Fermi level and the conduction band minimum (the valence band maximum) of the WSe2 layer. The Fermi level is set to zero and marked by red dotted lines.

在设计并实现基于二维过渡金属硫化物的高效逻辑器件时， 有必要在低势垒条件下制备n型和p型场效应晶体管. 根据肖特基在金属/半导体界面的模型， n型肖特基势垒高度(n-SBH)表示导带底与费米能级之间的能量差. 而p型肖特基势垒高度(p-SBH)可以由价带顶与费米能级之间的能量差来定义. 因此， n-SBH和p-SBH之和等于单层WSe2(1—x)(B， C， N， O)2x的带隙， 也就是说，Eg(WSe2(1—x)(B， C， N， O)x) = n-SBH + p-SBH.从图2(c)中可以直观看出， WSe2/graphene异质结的p-SBH为0.62 eV.

在分析WSe2/graphene异质结的电荷转移情况时， 本文计算了异质结的三维电荷密度差分， 如图3所示. 其中红色区域代表graphene价电子减少， 即正电荷聚集区; 蓝色区域代表Se原子表明聚集了负电荷， 即电子的增加. 当WSe2和graphene形成异质结后， graphene部分电子转移至WSe2， 从而导致单层WSe2表面聚集大量负电荷， 而graphene表面聚集大量正电荷， 进而形成一个由graphene指向WSe2的内建电场. 这是由于graphene费米能级高于单层WSe2费米能级， 电子从graphene的导带向WSe2转移. 这个结果与能带分析一致.

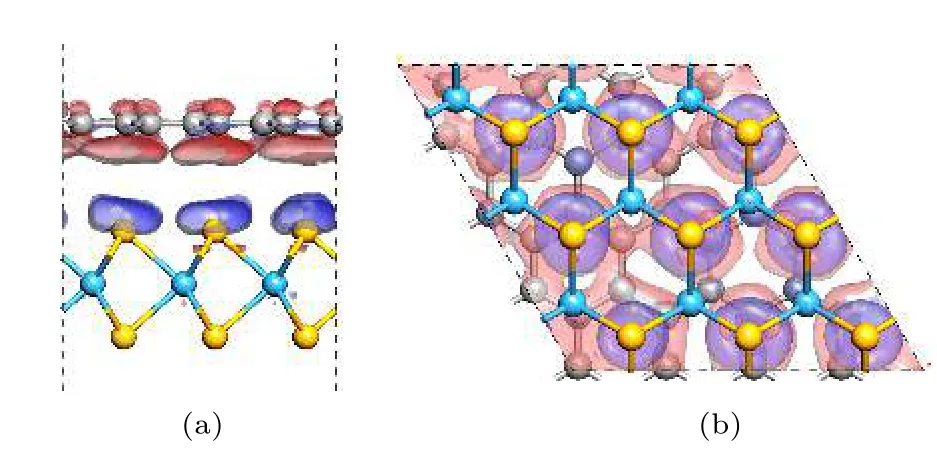
图 3 WSe2/graphene异质结三维电子密度差分图 (a)侧视图; (b)俯视图Fig. 3. Three-dimensional charge density difference plots of WSe2/graphene heterostructure: (a) Side view; (b) top view.

为了更好地明确WSe2/graphene异质结层间作用的机理， 对异质结的总态密度和分态密度进行了分析. 如图4所示， 在费米能级附近的价带顶主要由W 5d和Se 4p轨道组成， 而相对费米能级较远的导带底则是由C 2p和W 5d轨道组成.从图4(b)可以看出， graphene的轨道主要由2p轨道构成， 异质结中graphene的Dirac点仍然保留，即异质结中graphene表现出金属性质. 从图4(c)中可以看出， 异质结中WSe2的轨道主要由Se 4p以及W 5d轨道构成， 并表现出半导体性质， 能量为2 eV附近的导带中W 5d和Se 4p轨道出现重叠现象， 说明W原子与Se原子之间存在很强的轨道杂化， 主要以W 5d轨道为主， 并且有Se 4p轨道的贡献， 使W 5d轨道处于激发态的电子向Se 4p轨道跃迁， 使WSe2表面聚集更多的电子.综上， graphene与WSe2接触属于肖特基接触， 此时肖特基类型为p型， 态密度分析结果与能带分析结果一致.

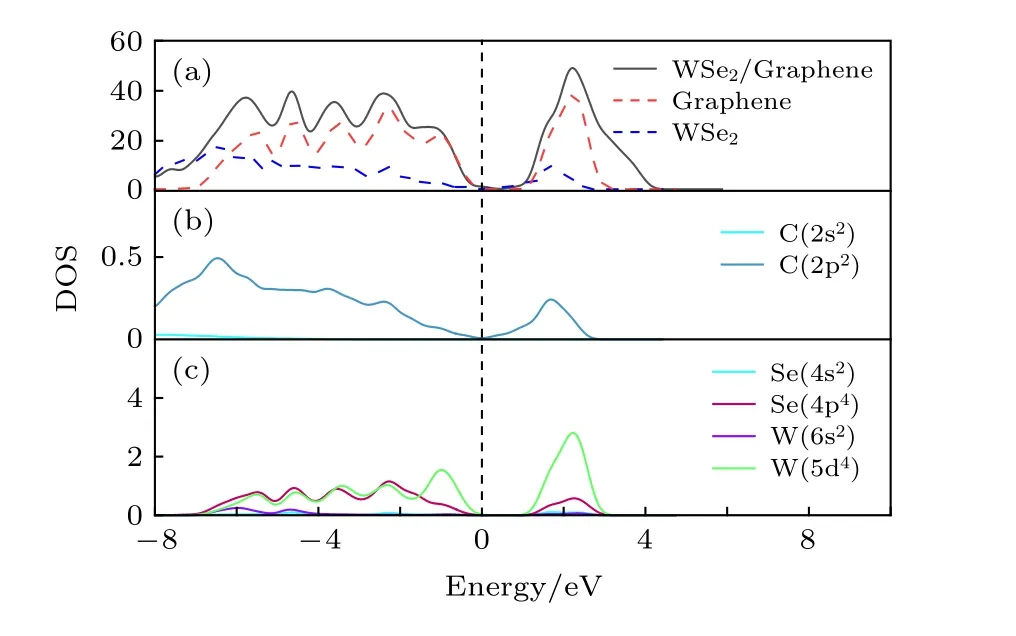
图 4 WSe2/graphene异质结的总态密度及分态密度图Fig. 4. Calculated total density of states and the corresponding partial density of states of WSe2/graphene heterostructure.

3.3 肖特基调控分析

异质结的肖特基调控主要指对肖特基类型的调控， 以及对肖特基势垒高度的调控. 实验和理论均表明， 通过外加电场、应力、掺杂、空位、表面修饰[62-64]等可以有效地控制异质结界面电荷的转移、肖特基势垒高度以及功函数. 因此， 本文通过掺杂的方法来影响WSe2/graphene异质结中的电子输运特性， 进而调控异质结的肖特基类型和势垒高度是完全可行的， 且具有重要意义. 对于单层TMDs材料呈现出X-M-X的三明治结构(其中X代表非金属， M代表金属)， 考虑到其表面很容易形成空位， 特别是非金属元素空位， 因此在TMDs材料掺杂过程中很容易引进非金属元素掺杂， 同时非金属元素很容易在空位与金属原子形成化学键[34]， 因此本文选用B， C， N， O替换WSe2中1个Se原子. 为了更好地了解非金属元素对WSe2/graphene异质结界面的影响， 首先分析了非金属元素对WSe2能带结构的影响， 如图5所示.

当掺杂O原子时， WSe2的能带形状没有发生太大的变化. 但是在掺杂N， C， B原子时， 在WSe2带隙间出现杂质能级. 当掺杂O原子时， WSe2带隙由1.62 eV变为1.66 eV导带底向上移动0.04 eV.这说明O原子掺杂对WSe2带隙的影响并不大.当掺杂N， B原子时， 在WSe2费米能级附近出现杂质能级导致带隙为零， WSe2呈现出严重的金属化， 导致WSe2的费米能级发生了移动. 当掺杂C原子时， 在WSe2导带底出现了杂质能级， 此时WSe2的带隙为0.78 eV. 通过4种非金属原子掺杂WSe2， 不难发现掺杂对WSe2的带隙有很大影响. 为了进一步研究掺杂对WSe2/graphene异质结肖特基势垒类型和高度的影响， 计算了掺杂异质结体系的能带， 如图6所示. 从图6(a)中可以看出， 掺杂O原子可以有效调控肖特基的类型;图6(b)， (d)看出， 掺杂N， B原子可以改变WSe2与graphene的接触类型; 图6(c)看出， 掺杂C原子可以降低WSe2/graphene异质结的肖特基势垒高度.

当掺杂O原子时， WSe2/graphene接触属于肖特基接触， graphene狄拉克点在费米面上未发生移动， 这说明graphene导带是满带. 相比于单层W9Se17O1能级， 不难发现异质结中的W9Se17O1能级下移0.77 eV， 这是由于形成异质结后graphene电子向W9Se17O1表面转移， 导致异质结中的W9Se17O1表面聚集电荷， 使得W9Se17O1电势降低. 此时W9Se17O1/graphene异质结中n型肖特基势垒高度为0.77 eV， 即n-SBH为0.77 eV，p型的肖特基势垒高度为0.79 eV， 即p-SBH为0.79 eV， 掺杂O原子使异质结类型由p型转化为n型， 且有效地降低了肖特基势垒的高度; 当掺杂N， B原子时， WSe2与graphene结合属于欧姆接触， 这是由于W9Se17N1， W9Se17B1表现出金属性质. 从图6中可以看出， W9Se17N1， W9Se17B1与graphene结合时， graphene的能级上移， 其狄拉克点位于费米能级的上方， 导带中存在未填充能级.并且， N， B掺杂之后的杂质能级穿过费米能级. 因此， graphene与W9Se17N1， W9Se17B1两者间不存在电势差， 导致异质结呈现欧姆接触. 当W9Se17C1与graphene接触时， graphene的狄拉克点在费米面上. 此时， W9Se17C1的杂质能级与异质结的费米能级之间的电势差为0.14 eV， 即n-SBH为0.14 eV， 而p-SBH为0.59 eV. 因此， 异质结类型为n型肖特基结. 综上， 当掺杂原子为O， C时，WSe2仍然保留半导体性质， 在与graphene形成异质结后由于WSe2的能带下移， 使得WSe2由p型转化为n型; 当掺杂N， B原子时， WSe2由半导体转变为金属， 与graphene形成欧姆接触. 因此， 通过对WSe2掺杂O， N， C， B可实现WSe2/graphene肖特基类型和势垒高度的调控.

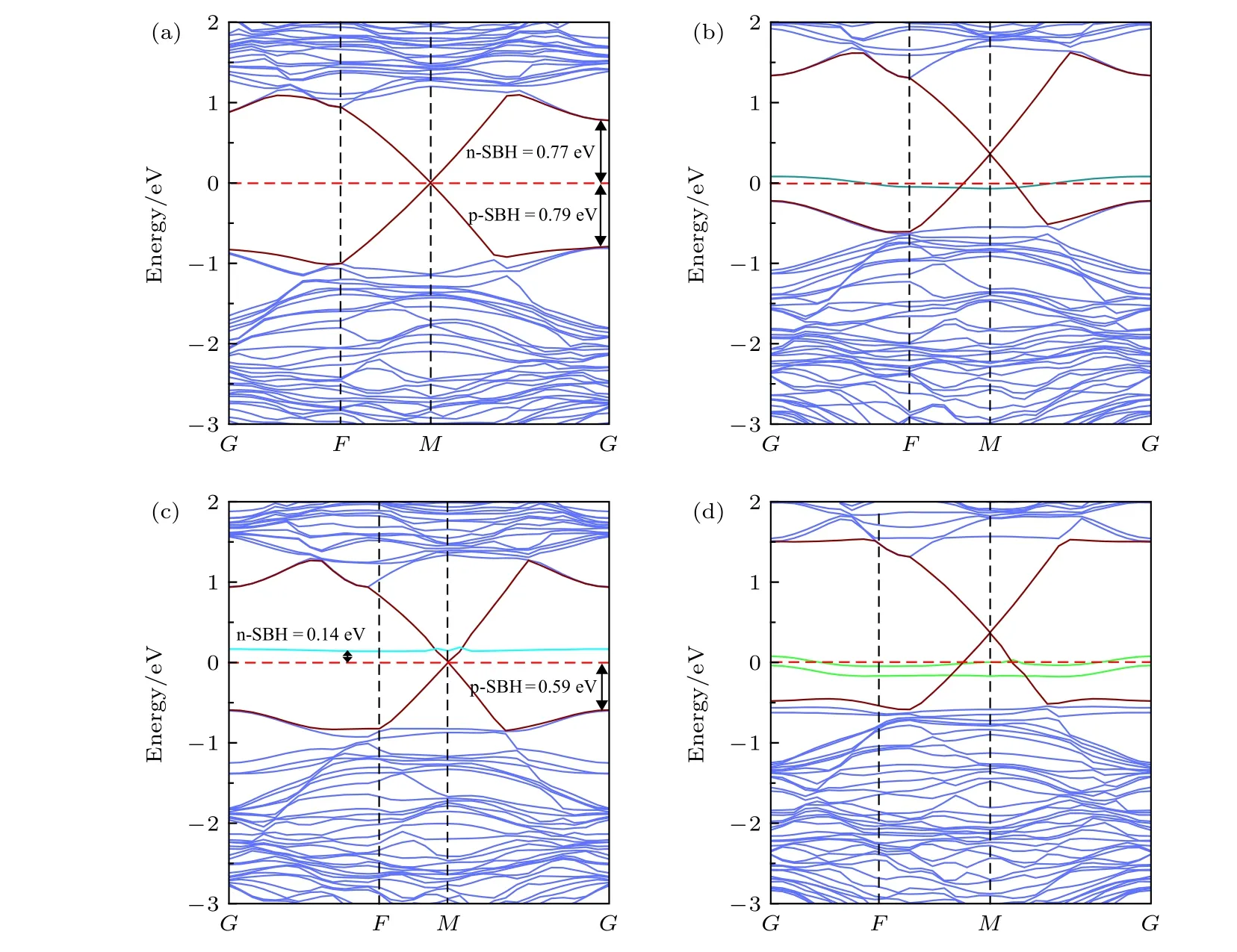
图 6 能带图 (a) W9Se17O1/graphene; (b) W9Se17N1/graphen; (c) W9Se17C1/graphen; (d) W9Se17B1/graphenFig. 6. Band structures: (a) W9Se17O1/graphene; (b) W9Se17N1/graphen; (c) W9Se17C1/graphen; (d) W9Se17B1/graphen.

4 结论

采用基于第一性原理的平面波超软赝势方法，研 究 了 掺 杂O， N， C， B等 非 金 属 原 子 对WSe2/graphene异质结物理特性的影响及调控机制， 并得到以下结果: 1) 对异质结界面结合能计算的结果分析表明， WSe2与graphene之间的结合以范德瓦耳斯力为主要作用力; 2) 能带计算分析表明， WSe2与graphene的耦合使得WSe2/graphene由耦合前的直接带隙变为耦合后的间接带隙， 且带隙由1.62 eV变为1.55 eV， 三维电子密度差分图进一步表明在界面内形成了由graphene指向WSe2的内建电场; 3) 当O原子掺杂WSe2与WSe2接触形成异质结时， 发现异质结由p型转变为n型， 且肖特基势垒高度低， 而当C原子掺杂WSe2时， 在WSe2导带底附近出现杂质能级，有效地控制了WSe2带隙宽度， 其与graphene结合形成较低的肖特基势垒; 4) 当B， N原子掺杂WSe2时， WSe2表现出金属性质， 与graphene结合形成异质结时， 异质结表现为欧姆接触.