碳纤维复合材料壳体轴压稳定性分析与试验验证

栗永峰，周伟勇，张 磊，杜鹏程

(1.国防科技大学 空天科学学院，长沙 410073；2.中国航天科工集团有限公司六院四十一所，呼和浩特 010010；3.中国人民解放军96901部队，北京 100095)

0 引言

碳纤维复合材料以其较高的强度和较低的密度已广泛用于固体火箭发动机壳体[1]。由于壳体除了承受发动机工作时的内压载荷外，还承担着弹(箭)体起竖、翻转、飞行时产生的轴压载荷，因此在产品设计阶段必须针对发动机壳体的受力进行详细计算和验证。

由于碳纤维材料本身的各向异性、微观构造的不均匀性以及壳体屈曲时所固有的几何非线性，使结构稳定性问题变得异常复杂，其研究水平远远落后于相应的金属壳体。目前，壳体强度设计的理论和研究方法已经非常成熟，计算结果与试验结果吻合较好，而对复合材料壳体刚度设计的研究方法则相对落后，分析结果与实际情况存在较大差异。

轴压载荷通过发动机壳体前、后裙传递至圆筒段。通常情况下，前、后裙以零件方式预制，在发动机壳体制作过程中采用插入方式粘接，再进行环向捆绑成型。轴压载荷作用下裙连接区的受力属于强度问题，在《基于内聚力模型的复合材料壳体裙粘接性能研究》一文中进行了专门论述。因此，本文重点研究讨论圆筒段的轴压稳定性。

复合材料壳体轴压稳定性问题已经引起国内外学者的广泛关注。陈汝训[2]将复合材料圆筒看作正交异性体，推导了临界轴压的计算公式，讨论了通过壳体内压和轴压试验确定复合材料圆筒弹性常数的工程方法；Parnas等[3]采用经典的层合理论和平面应变模型求解了纤维增强压力容器在内压载荷、轴向力和旋转体力条件下的解析解。王珂晟[4]针对一般的纤维缠绕情况，应用板壳理论和复合材料的力学关系式讨论了复合材料圆筒壳在轴压作用下临界载荷的计算公式，并提出了一种将遗传算法和经典算法结合起来的新算法-混合遗传算法。这些研究工作目前尚停留在理论层面，未进行有效地试验验证。

碳纤维复合材料壳体的结构参数和缠绕参数将直接影响壳体的受力状态。Liang等[5]针对纤维缠绕压力容器的结构尺寸、缠绕角度等参数，结合Tsai-Wu失效准则开展了缠绕压力容器封头优化设计研究。Park等[6]分析了沿厚度方向采用不同缠绕角对纤维缠绕复合材料结构的应力水平影响。Chang等[7]分析了纤维缠绕压力容器在最大爆破压强下最优缠绕角，并通过理论分析、有限元分析和试验方法进行验证。Cohen[8]通过试验研究了影响复合材料容器质量和强度的制造和设计变量，发现层叠顺序、缠绕拉力、缠绕时间等因素都对容器的质量和强度产生一定的影响。伍天健[9]通过复合材料铺层参数和材料常数，计算出纤维弹性主方向的弹性系数，然后在求得复合材料圆筒轴向和环向的复合弹性系数，利用胡克定律计算出壳体的临界轴压。

针对碳纤维复合材料壳体轴压稳定性问题，采用数值模拟、理论推导和试验验证相结合的方法，探索出适合于工程实际应用的碳纤维复合材料壳体稳定性计算方法，并利用复合材料的可设计性，研究铺层相关参数对轴压稳定性的影响规律。

1 复合材料壳体临界轴压理论计算方法

基于层合板理论计算出壳体拉压刚度矩阵[A]6×6，在轴向载荷作用下，复合材料壳体圆筒段等效弹性参数计算公式为

(1)

式中E1为等效轴向弹性模量；E2为等效环向弹性模量；μ12为轴向力作用引起环向变形对应的等效泊松比；μ23为环向力作用引起轴向变形对应的等效泊松比；G12为等效剪切模量。

复合材料壳体是轴对称结构，将其视为正交异性体，在忽略刚度矩阵B、D影响的情况下，临界轴压可按式(2)计算[2]：

(2)

式中Tcr为临界轴压；t为壳体厚度；E1为等效轴向弹性模量；E2为等效横向弹性模量；μ12为等效轴向泊松比；μ23为等效横向泊松比；k为试验修正系数，一般取0.3～0.5。

从式(2)可看出，壳体的临界轴压与壳体的厚度和弹性常数有关，而与壳体直径和长度无关。

2 复合材料壳体临界轴压分析方法

工程研制过程中，由于不同产品的结构尺寸有所差异，直接采用真实产品进行试验存在很大局限性。一是试验条件所限，一般不具有满足所有产品验证的大型设备设施；二是试验成本太高，子样数少，且由于对象自身特点，不宜研究出普遍规律；三是产品研制过程中技术状态尚未固化，试验结果在后期可能成为无效子样。基于以上几个因素和理论分析的指导，本文以φ150 mm圆筒为研究对象，探索研究常温下T700碳纤维复合材料壳体临界轴压载荷的变化规律。

2.1 碳纤维增强复合材料壳体制备方案

以φ150 mm圆筒为研究对象，研究临界轴压随铺层参数的变化规律。选用T700碳纤维混合环氧树脂进行纵环向交替缠绕，碳纤维缠绕角为20°、30°和40°，纤维体积含量为60%。可用M40J-12k无纬布替代碳纤维以增加壳体的刚度。 壳体长 1200 mm，直径为150 mm。图1给出了碳纤维复合材料壳体结构示意图。表1给出了复合材料壳体筒段铺层顺序。

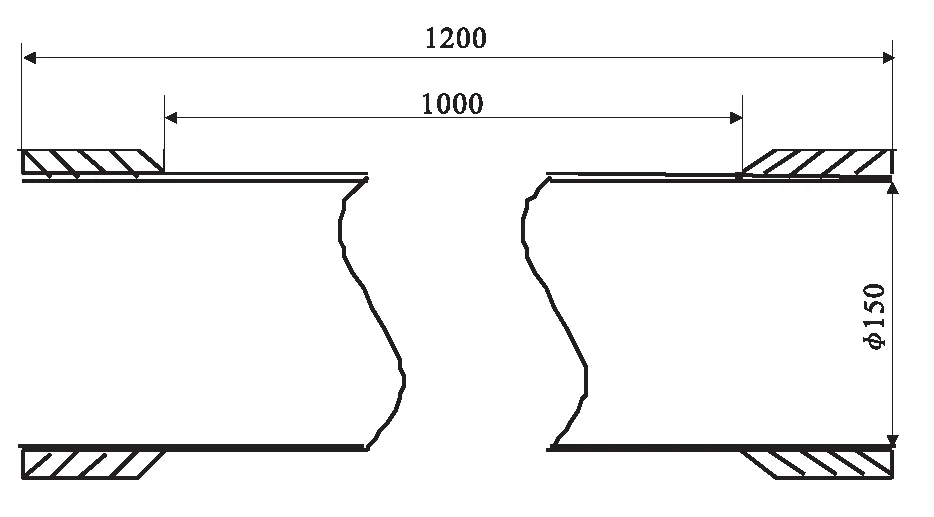
图1 φ150 mm碳纤维圆筒结构示意图

表1 缠绕参数

2.2 φ150 mm圆筒临界轴压有限元分析方法

采用有限元软件ABAQUS对复合材料壳体进行轴压分析，相关的方法在碳纤维壳体轴压计算领域有成熟的应用[10]。图2给出了有限元计算1∶1全模型，为保证有限元计算可靠性，复合材料圆筒和加强铝框均为六面体结构网络，复合材料圆筒划分为单层网格用于后续铺层见图2(a)。复合材料圆筒和加强铝框分别采用SC8R连续壳单元和C3D8R三维应力单元，单元尺度为10 mm，网格数分别为11 136和1428(图2(b))。在有限元计算中，模型一端加强框端面施加固定约束，另一端加强框端面施加单位载荷的轴向力。

2.3 φ150 mm圆筒轴压试验验证方法

采用静力试验测试系统进行φ150 mm圆筒轴压破坏试验。图3给出了轴压试验测试装置图。在壳体轴向上均匀布置4组应变片，每组应变片布置在相隔90°的4条象限线上，用于监测加载后圆筒的受力是否均匀，分析轴压载荷下的应变变化规律。试验开始前，预先加载20 kN的轴向力，以检查应变片是否正常。正式加载时加载速度为1 kN/s，直至壳体破坏。

3 结果与讨论

3.1 φ150 mm圆筒临界轴压分析

以φ150mm圆筒为研究对象，通过理论计算和有限元分析预示碳纤维复合材料壳体临界轴压载荷。

(a)Layers structure

(b)Gird

图3 轴压装置

表2给出了缠绕角为20°、30°和40°时壳体的等效弹性常数。当缠绕角由20°增大至40°时，等效轴向弹性模量E1由70.86 GPa迅速降低至35.67 GPa，而等效横向弹性模量保持约72～73 GPa不变；壳体等效轴向泊松比由0.173增大至0.264，而等效横向泊松比显著增大，由0.176增大至0.547。由此可看出，当缠绕角增大时，轴向刚度减小，对横向刚度的影响较小。当缠绕角由20°增大至40°时，轴向泊松比及横向泊松比均增大。因此，壳体在受轴压载荷时横向应变增大。

从试验数据看，应变数据均与轴压载荷呈线性变化，达到近7000 με，失稳位置均在筒身段，见图4。

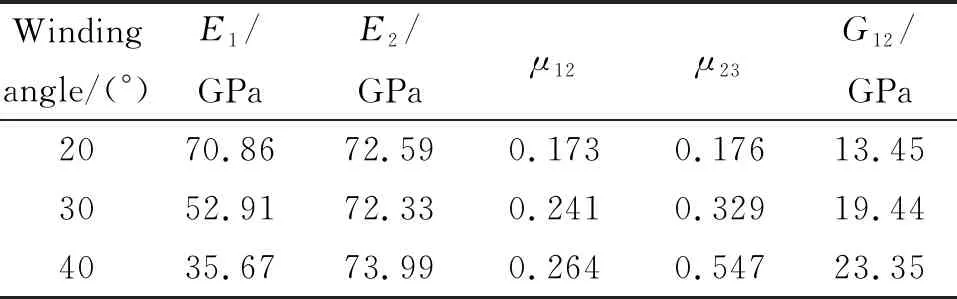
表2 等效弹性常数

图4 轴压试验后圆筒的破坏情况

表3给出了分别采用理论计算、有限元计算以及试验测定的方法求得了壳体Ⅰ的临界轴压。根据求得的等效弹性常数，采用式(2)计算了缠绕角为20°、30°和40°时壳体临界轴压载荷，按照修正系数范围计算结果分别为195.8～652.7 kN、173.3～288.8 kN和149.3～248.8 kN，这与壳体等效轴向弹性模量的变化规律一致。采用轴压试验测试的缠绕角为20°、30°、40°时壳体的临界轴压分别为286、、185、145 kN。由此可知，采用轴压试验的方法获得了壳体的轴压载荷在理论计算值范围之内。在理论计算时，比例系数取约0.4时与试验测试结果较为接近。

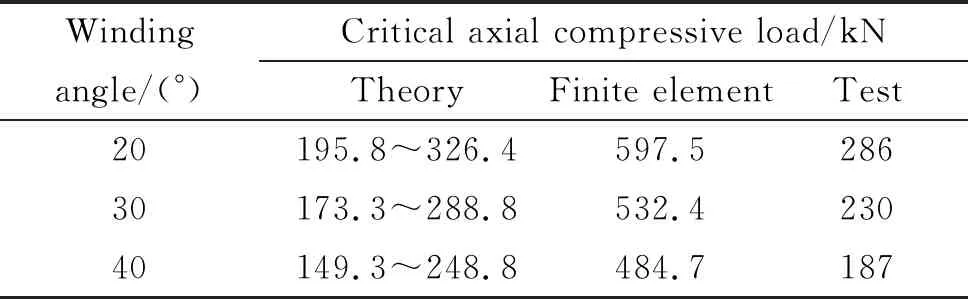
表3 壳体临界轴压

采用有限元计算方法计算的缠绕角为20°、30°、40°时φ150 mm圆筒临界轴压分别为597.5、532.4、484.7 kN。由于有限元计算是在理想状态下进行，未考虑产品缺陷对临界轴压的影响，其值大于试验测试结果。从测试结果分析，在有限元计算值基础上，修正系数取0.35～0.45与试验测试结果较为接近(缠绕角大时修正系数取下限)。

3.2 纤维体积含量、缠绕角对临界轴压的影响规律

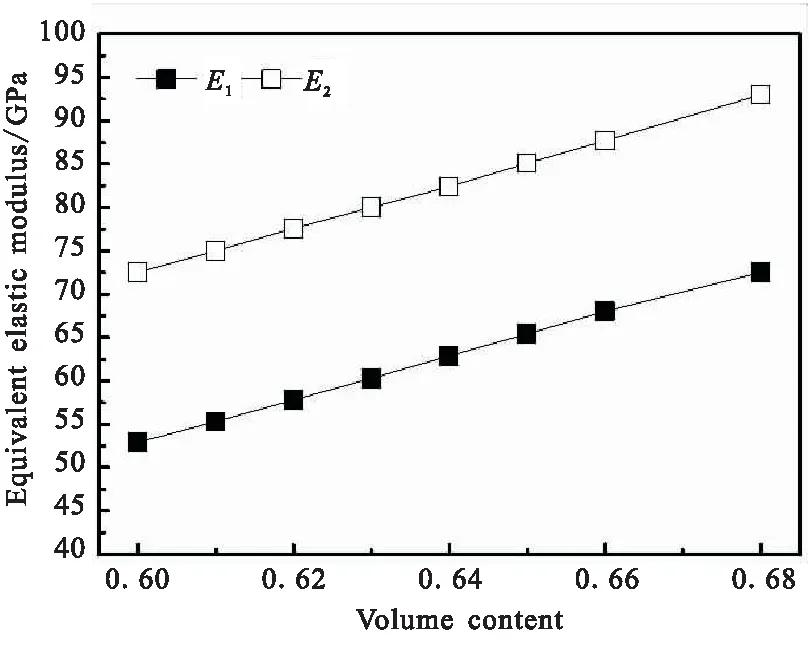
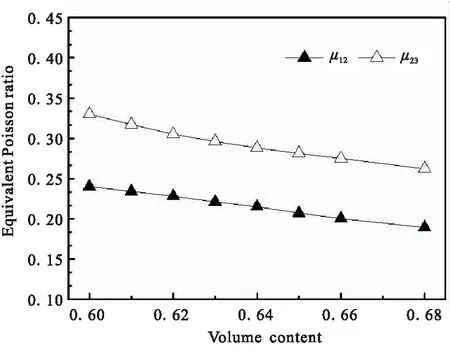
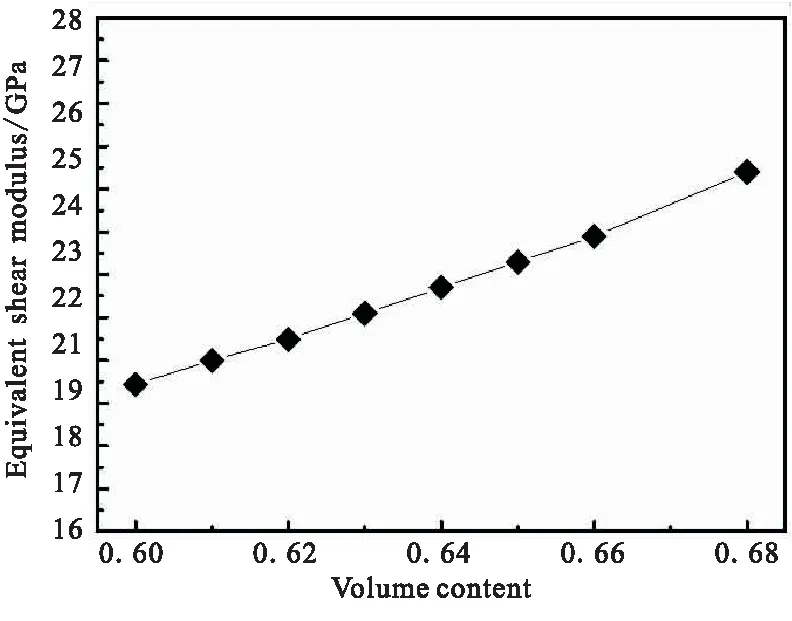
根据复合材料壳体临界轴压计算式(2)可知，弹性常数是决定壳体临界轴压大小的关键参数。弹性常数与材料性能和铺层参数密切相关[11-12]。因此，本文以φ150 mm圆筒为研究对象，研究不同碳纤维体积含量和纤维缠绕角对等效弹性常数的影响规律。图5给出了等效弹性参数随碳纤维体积含量变化的曲线。

(a)Equivalent elastic modulus

(b)Equivalent Poisson ratio

(c)Equivalent shear modulus

从图5可看出，等效轴向模量E1、等效环向模量E2和等效剪切模量G12随着纤维体积含量的提高而增大，轴向力作用引起环向变形对应的等效泊松比μ12和环向力作用引起轴向变形对应的等效泊松比μ23随着纤维体积含量的提高而减小，并且均呈线性变化；纤维体积含量每提高1%，E1和E2均增大约2 GPa，μ12和μ23均减小约0.01， 增大约0.2 GPa。这主要是由于碳纤维是主要的承力载体，碳纤维体积含量增大，等效弹性常数越大。

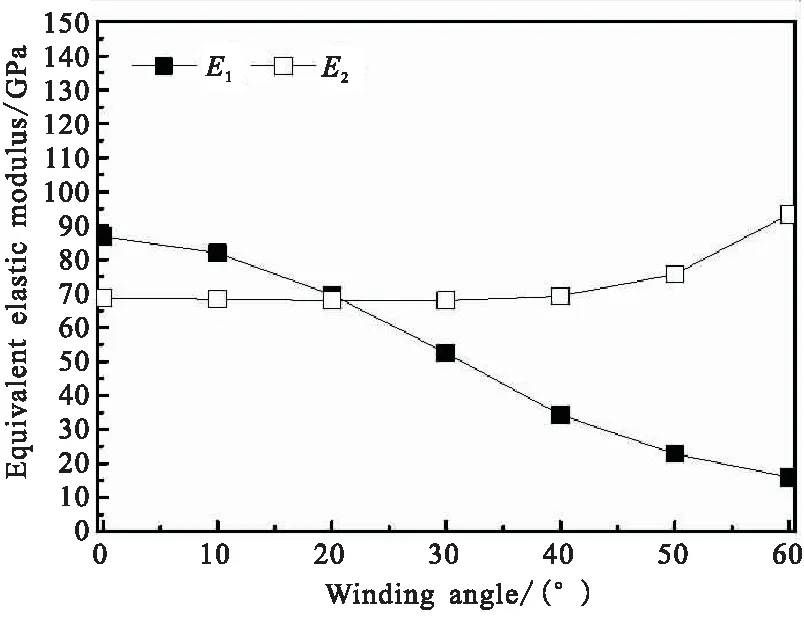
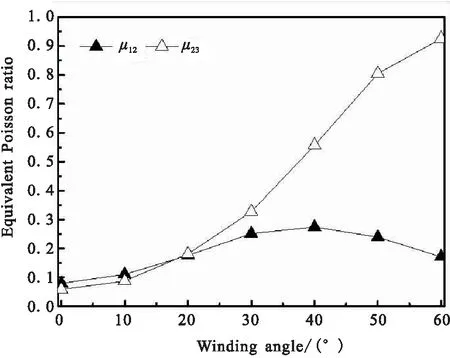
图6给出了等效弹性参数随纤维缠绕角变化曲线。

(a)Equivalent elastic modulus

(b)Equivalent Poisson ratio

(c)Equivalent shear modulus

从图6可见，等效轴向模量E1由缠绕角0°时的86.8 GPa降低至缠绕角60°时的14.7 GPa。等效环向模量E2在缠绕角为0°～45°时保持基本不变，约为69 GPa，缠绕角超过45°时逐渐增大至60°时的93.3 GPa。等效轴向泊松比μ12呈先增大、后减小的趋势，缠绕角为0°时μ12=0.08，缠绕角为40°时达到最大值0.274。等效环向泊松比由缠绕角为0°时的0.06逐渐增大至缠绕角60°时的0.97。等效剪切模量G12随着缠绕角增大呈先增大、后减小的趋势，缠绕角为45°时达到最大。

图7给出了不同纤维体积含量时φ150 mm圆筒的临界轴压，图8给出了不同缠绕角时φ150 mm圆筒的临界轴压。可看出，临界轴压载荷随纤维体积含量提高而增大，随着缠绕角的增大而逐渐降低。其中，等效轴向弹性模量对壳体临界轴压起到主要的影响作用。Priyadarsini等[13]的研究同样证实碳纤维壳体的力学性能除了由纤维与基质本身的属性决定，还受纤维的铺层、壁厚、缺陷等因素影响。

图7 碳纤维体积含量随壳体临界轴压变化规律

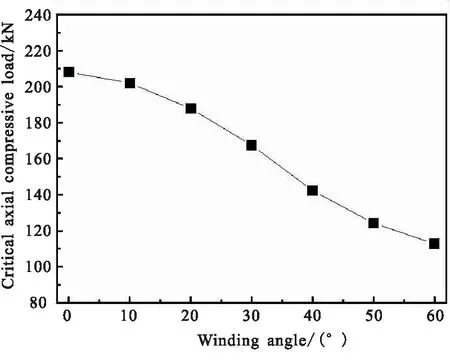
图8 缠绕角随壳体临界轴压变化规律

3.3 提升轴向刚度的技术途径

为增加轴向刚度，在以30°缠绕角缠绕壳体的基础上分别增加1、2、3和4层0°铺层来进行轴压破坏试验。图9给出了φ150 mm圆筒临界轴压与0°铺层数的关系。从图9可看出，临界轴压载荷随0°铺层逐层增加呈线性增长变化。相比原状态(0°铺层为0)，增加0°铺层1、2、3和4层轴压承载能力分别提高57%、107%、156%和208%；随着铺层的增加其重量相应增加，重量分别增加3.9%、8.1%、12.4%和16.9%。因此，增加0°铺层能够大幅度提高复合材料壳体圆筒段轴压承载能力，在壳体重量允许调整的情况下，增加0°铺层是提高复合材料壳体刚度的有效措施之一。

图9 0°铺层与临界轴压变化规律

4 结论

(1)有限元计算结果未考虑产品材料缺陷和几何缺陷，计算结果较试验测试结果大。采用复合材料壳体临界轴压计算方法，修正系数k=0.4的计算结果与试验测试结果接近。

(2)壳体的刚度是影响壳体临界轴压的主要因素，等效轴向弹性模量对壳体临界轴压的贡献要大于等效横向弹性模量。

(3)相比提高纤维体积含量，增加0°铺层可显著提升复合材料壳体轴向刚度，且对提高刚度的贡献远大于其重量增加。因此，在壳体重量允许调整的情况下，增加0°铺层作为提高复合材料壳体刚度首选；重量要求严格时，考虑工艺上控制纤维体积含量，以提高壳体轴压承载能力。