从旋转视角看待全等三角形

于方舟

【摘 要】 旋转是图形运动中的三种全等变换之一，经过旋转之后的图形与原图形是全等的，因此，可以借助旋转变化的方法帮助我们识别复杂图形中的全等图形。本文主要从简单的旋转模型开始，以具体题型为例，寻找复杂图形中所具有的简单模型，进一步理解旋转变化。

【关键词】 旋转变化;全等图形;三角形

全等三角形是初中几何的重点内容，旋转变换是初中数学三大变换之一，一道证明三角形全等的题目，如果从旋转变换的视角去寻找三角形全等的条件，往往会使得寻找的目标更为明确，对图形的认识也更为清晰。

一、旋转模型

如图1，在等边三角形ABC和等边三角形ADE中，AB和AD在同一条直线上，连接BE、CD，分别与AC和AE相交于点G、H，BE和CD的交点记作点F。求证：△ABE≌△ACD。

分析：本题是旋转的基本模型，由题意：△ABC和△ADE都是等边三角形，可得AB=AC，AD=AE，∠BAC=∠EAD=60°，同时加上公共角∠GAH，即可得∠BAE=∠CAD，即能证得△ABE≌△ACD（SAS）。在这一问题中，△ABE绕点A顺时针旋转60°与△ACD重合，因此寻找对应线段和对应角就显得更为明显。 我们可以从这一问题中，归纳出一个基本的旋转模型，如图2，两个三角形绕着一个顶点旋转即可重合，利用旋转变换的视角，即能化繁为简，在复杂的几何图形中，分辨出基本模型。

二、旋转模型的适当变形

如图3，以△ABC的两边AB、AC为边，分别向外作等边三角形ABD和等边三角形ACE，连接BE、CD，相交于点F，请回答以下问题：（1）判断BE与CD之间的大小关系;（2）判断∠BFD与∠BAD之间的大小关系。

分析：在这个图形中，可以将△ABE绕着点A顺时针旋转得到△ADC，因此解决这个问题，首先证明△ABE≌△ADC（SAS），即可得到BE=CD。在判断∠BAD与∠BFD的大小关系时，可以利用图形中存在的“8字模型”。在△ADG和△FGB中，∠AGD=∠FGB（对顶角），∠ADG=∠FBG（由三角形全等得到对应角相等），因此，∠BFG=∠DAG=60°。“8字模型”也是由旋转模型得到的一个结论，通过三角形全等，得到一组对应角相等，再根据对顶角相等，即可得到两个三角形中的另外一组角相等，由“8字模型”，可以很快找到度数相等的角。

接下来，对于图3再作适当变形，通过旋转模型，解决问题。

如图4，以△ABC的AB、AC为腰，向三角形外作等腰三角形ABD和等腰三角形ACE，顶角∠BAD=∠CAE=α，连接BE、CD，相交于点F，连接AF，请证明以下结论：（1）∠BFD=α;（2）∠DFA=∠EFA。

分析：（1）由旋转模型，很容易得出△ABE≌△ADC，从而得到对应角相等，即∠ABE=∠ADC，再由“8字模型”，可以得到∠BFD=∠BAD=α。

（2）要证∠DFA=∠EFA，可证∠DFA与∠EFA所在的三角形全等。△ABE与△ADC通过旋转可以重合，那么这两个三角形的对应元素也是始终相等的，因此可以联想到，旋转三角形中的重要对应线段——高线，从而构造全等三角形。过点A作AG⊥CD于点G，AH⊥BE于点H，如图4。可以得到AG=AH（AG、AH可以看成是△ABE与△ADC对应边的高，因此它们是相等的;也可通过证明△ABH≌△ADG（AAS），得到AG=AH。在Rt△AGF和Rt△AHF中，AG=AH，AF=AF，所以Rt△AGF≌Rt△AHF（HL）。所以∠AFG=∠AFH，即∠DFA=∠EFA。

思维拓展：如图5，以△ABC的AB、AC为边向三角形外作正方形ABDE、ACFG，连接BG、CE，相交于点H。证明：（1）BG⊥CE;（2）∠EHA=∠GHA。

三、模型方法迁移，解决难题

有了上述问题做铺垫，解决下面的问题就会显得得心应手。

如图6，已知△ABC和△DCE均是等边三角形，点B，C，E在同一条直线上，AE与BD相交于点H，AE与CD相交于点G，AC与BD相交于点F，连接HC，FG，有下列结论：①AE=BD;②AG=BF;③FG∥BE;④∠BHC=EGC。其中正确的结论是_。

分析：在此图形中，可将△BCD绕点A顺时针旋转60°，即可与△ACE重合，因此，这是一个典型的旋转模型。结论①易证;同样，可将△BCF绕点C顺时针旋转60°，即可与△ACG重合，故有AG=BF，结论②正确;由△BCF≌△ACG，有CG=CF，又∠FCG=60°，所以△CFG是等边三角形，所以∠CFG=∠ACB=60°，所以FG∥BE，结论③正确;要证明∠BHC=∠EGC，由上述探究得到启发，过点C作CM⊥BD于点M，CN⊥AE于点N，如图6。CM、CN是旋转模型中两个全等三角形对应边上的高，故CM=CN，易证Rt△CMH≌Rt△CNH（HL），所以∠CHM=∠CHN，即∠BHC=∠EHC，结论④正确。所以，正确的结论有①②③④。

通过对上述旋转模型的分析和变形，相信我们对此类问题不会再感到迷惑了吧，我们接下来就挑战一下自己吧！

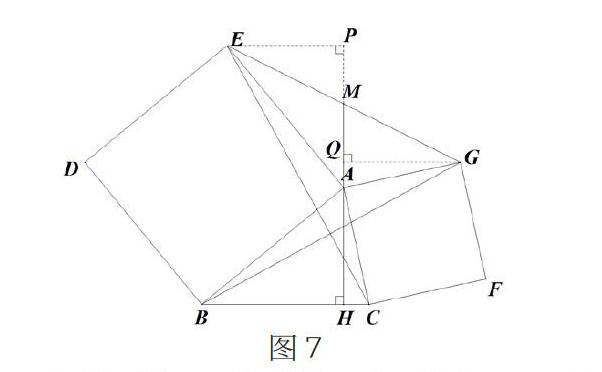
如图7，在锐角三角形ABC中，AH是BC边上的高，分别以AB、AC为一边，向外作正方形ABDE和ACFG，连接CE、BG和EG，EG与HA的延长线交于点M，下列结论：①BG=CE;②BG⊥CE;③∠EAM=∠ABC;④AM是△AEG的中线。其中正确的结论是_。

思路点拨：由上述探究，可知①②正确。 过点E、G分别作直线HM的垂线，垂足分别记作P、Q，如图7。易证Rt△ABH≌Rt△EAP，所以∠EAM=∠ABC，AH=EP;同样方法证明Rt△ACH≌Rt△EAQ，所以AH=EQ，因此EP=EQ，接下来可证Rt△EPM≌Rt△GQM，得到EM=GM，即AM是△AEG的中线。因此，③④正确。

总结：旋转模型可以帮助我们在复杂图形中抽象出基本图形，迅速找到图形中存在的全等三角形，利用旋轉图形的对应线段也是相等的，可以在添加辅助线时给予启发，构造全等图形。 旋转思想，可以帮助我们化繁为简，切中图形要点，使困难问题迎刃而解。