浅议“图式表征”有效解决小学低年级数学问题的作用
2020-06-29李结云
李结云

【摘要】图式表征的运用从知识理解的角度来说是一种直观有效的方法之一,可以使数学问题变得直观易懂,更适合小学生的心智。目前,有不少教师因教学理念思想跟不上新课改理念,“穿新鞋走老路”,带来的往往是越往高年级,学生的数学素养就会慢慢减退,学困生也逐渐增多,对于此,笔者认为在低年级解决问题的教学中需要尽可能多地为孩子创造图式表征的机会,让学生在画图中学会数学地思考,学会科学、有效地表征。从而使数学课堂教学成为变“教方法”为“策略指导”的高效性新课改课堂。
【关键词】数学问题解决;思维能力;图式表征;解题策略
在新一轮课改的进程中,小学生数学问题解决思维能力的培养得到了高度的关注。在一线教学中,我们仍旧发现一些教师会认为小学生在解决问题时只要有了经验做铺垫,就自然而然地会列式解答,而不需要老师在课堂上引导分析其中的数量关系或空间结构;甚至有的老师认为低年级的数学知识很简单,无需老师讲学生就会的,只要抓好学生的计算能力就行了,根本不用考虑数学思维分析的体验。这样久而久之学生的数学思维得不到提升和拓展,问题解决的策略不能被激活,到了中高年级,学生的数学素养慢慢减退,学困生也会慢慢增多。为了避免这种负面的状态,笔者认为在低年级解决问题的教学中需要尽可能多地为孩子创造图式表征的机会,让学生在画图中学会数学的思考,学会科学、有效的表征,从而使数学课堂教学成为变“教方法”为“策略指导”的高效性新课改课堂。
一、说话“图式表征”
1.图式
最早提出图式这个概念的心理学家是巴特莱特(F.C.Bartlett,1932)。他通过一系列的心理实验对比后将图式界定为:“关于过去反应或以往经历的一种主动组织。”
2.表征
它是认知心理学的核心概念之一,指信息或知识在心理活动中的表现和记载的方式,是外部事物在心理活动中的内部再现。曾经有美国认知心理学专家认为:表征是问题解决的一个中心环节,是数学问题转化成数学策略的桥梁,是学生自我构建、自我表达、自我建模的外在表现形式,是学生之间最直观的交流途径。
3.“图式表征”
图式表征既是一种思维形式也是一种解题策略,是学生运用已有经验,将脑中“心里图画”用图式等多种形式表现出来,是对动手操作的纠正、补充、细化和深化,是一种最有效、最常用的表征问题的方法之一,其符合小学生的思维特点和心智,可以使数学问题变得直观、明了。图式表征包括画线段图、树图、集合图、示意图等,是学生最终向符号表征提升的基础。在解决问题中使用图式表征思维,能促进学生主动积极参与学习的理解活动。低年段小学生的解决问题思维正处于具体形象阶段,在教学中让学生把自己对问题解决过程的思考用图表形式呈现,让其更好地感受到解决问题的过程,达到发展学生思维水平、培育思维能力和形成思维习惯的目的。
二、“图式表征”便于直观理解,疏通问题分析
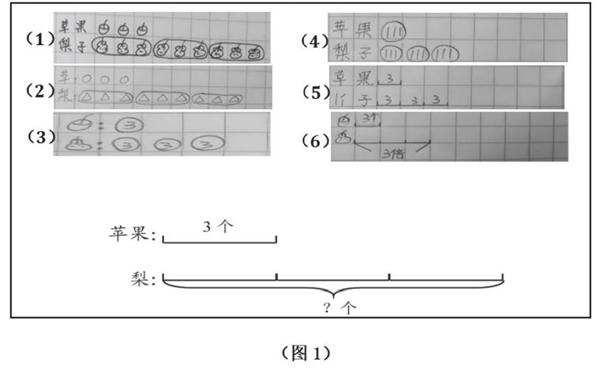
低年级的学生因其年龄小,识字少,理解抽象数学思维的能力弱,不能凭借单纯读图和说图来理解和思考问题。因此,动手画一画直观的图式,就能为学生搭好解决抽象数学问题的“桥”。如“求一个数的几倍是多少 ”(三年级上册)的教学,老师从学生已有的知识经验和活动经验出发,引导学生尝试用个性化的图式进行图式表征,并鼓励学生大胆汇报,在汇报时教师有意对学生的作品按层次呈现(如图1),让学生在视觉对比上感受图式之间的优越性,最终感受线段图的简捷,让学生逐步建立起“1格代表3”的数量表象,经历具体到抽象的过程。经历了教师这样的引领后,学生对线段图这种图式表征的记忆和理解一定会更深刻,对于“倍”这一知识的理解也会更为透彻。
又如一年级的《20以内的加减法解决问题》(如图2),教学时如果让学生单纯地读题目主题图、说图中的话,很多学生不能清楚地理解“ 作为标准的那个人两次都没数到”这一思维关键点,往往就会算成9+5=14(人),但如果让学生用图式画出来(如图3):三角形代表标准的那个同学,圆代表其他同学,从图上学生就能看出作为标准的那个人前面有9个人,后面有5个人,“那个人”是没有数到,最后要加上“那个人”才是总人数,正确列式为9+5+1=15(人)。通过这样的图式,这道题目的题意就非常清晰了。
三、“图式表征”促使数形灵活结合,明析数量关系
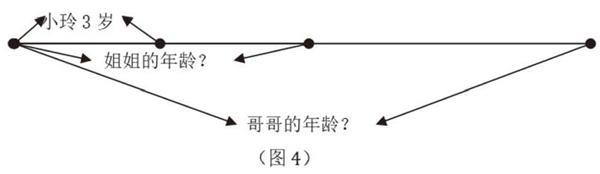
在低年级的一些练习题里,有些问题的文字表述并没有直接呈现已知信息,有些应用题的数量关系不能直接感知,面对这些题目,低年级的学生们往往不知从何入手分析,那么,这时候引导学生借助简单的图形、符号和文字所作的示意图或线段图来表征,借此理解题中隐藏的数量关系,沟通题目已知条件和问题内在关系,显得更为重要。學生可以通过直观形象的图式,能清晰地找到解决问题的办法。如:(一年级课堂拓展练习)小玲今年3岁,小玲的年龄是姐姐年龄的一半,姐姐的年龄是哥哥年龄的一半。请问哥哥今年多少岁?学生在读题后就眉头紧锁了,对该题的数学信息和数量结构模糊不清,这时引导学生用线段图(如图4)一步一步标注已知信息,问题自然迎刃而解了。
又如“由总数推出一半”的解决问题:玲玲有20枝铅笔,其中绿色铅笔有10枝,红色铅笔是绿色铅笔的一半,剩下的就是黄色的铅笔。问她有几枝黄色铅笔?用图式表征来分析理解这类型题目的数量关系是最直观的方法。老师引导学生画示意图(如图5)把已知的数学信息标注出来后,那么上述题目的数量关系就很清晰的展现孩子们眼前。
综上所述,图式表征能将解决问题的过程形象地呈现,激发学生的灵感与想象,激活学生的思维。纵观小学数学教材的知识体系,在低年段的问题解决教学中有着很多相关的内容可以有效地利用图式表征策略来帮助学生更直观地分析问题,从而准确有效解决问题,例如:关于概念理解的问题、思考题、有关“倍”的解决问题、求两个数相差多少的解决问题等等,这些教学都值得我们重视图式表征策略的利用,值得我们放慢教学推进的匆匆脚步,在引导和启发孩子不断运用和提升中培养他们利用图式表征分析数学问题的思维习惯,从而减轻解决问题过程中的记忆负担,达到直接有效寻找出解决问题的突破口,形成解决问题的基本策略。
【参考文献】
[1] 董妍,路海东.小学生应用题表征的类型和特点[J].心理科学,2004,27(6):1352-1355.
[2] 袁艳梅.数形结合思想在小学数学教学中的渗透[J].中小学教学研究,2011,03.
